【深度學習】——損失函數(均方差損失和交叉熵損失)
損失函數在【機器學習基礎】中有所提及,在深度學習中所使用最多的是均值平方差(MSE)和交叉熵(cross entropy)損失,這裡著重介紹一下這兩個損失函數及其在tensorflow中的實現。
1. 均方差損失
均方差就是預測值與真實值之間的差異,其公式為:
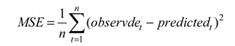
一般對於標籤是實數且無界的值的時候,損失函數選用均方差損失。
均方差在tensorflow中的實現也比較簡單:
MSE = tf.reduce_mean(tf.pow(tf.sub(logits, labels), 2.0))
MSE = tf.reduce_mean(tf.square(tf.sub(logits, labels)))
MSE = tf.reduce_mean(tf.square(logits, labels))
2. 交叉熵損失
交叉熵損失有sigmoid交叉熵、softmax交叉熵、Sparse交叉熵、加權sigmoid交叉熵。
2.1 sigmoid 交叉熵損失
對於sigmoid交叉熵,網路的輸出值經過sigmoid函數,然後再與真實值計算交叉熵,但是由於sigmoid的對映是相互獨立的,相加並不等於1。
因此,sigmoid對於二分類,最後的輸出為一維的數值(LR演演算法),表明屬於該類別的概率p,而不屬於該類別的概率則為1-p;
而對於多分類任務,輸出的最後一維為m維,也就是m個類別,每一維表示屬於該類別的概率,因此這裡sigmoid將不再適用。
對於多標籤的分類,相當於多個二分類任務,最後一層輸出為m維(m個標籤),然後用sigmoid計算屬於每個標籤的概率,大於0.5則表明屬於該標籤。
在tensorflow中sigmoid交叉熵損失:
tf.nn.sigmoid_cross_entropy_with_logits(logits, labels, name=None)
logits為輸出層的值,該值沒有經過simoid之前,labels為標籤。
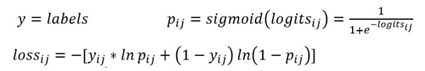
sigmoid交叉熵損失適用於每個類別相互獨立但互不排斥的多標籤分類問題,例如一幅圖可以同時包含一條狗和一隻大象。
output不是一個數,比如5個樣本三分類問題,且一個樣本可以同時擁有多類,一個樣本會在每個類別上有一個交叉熵,輸出也就是5*3矩陣。
y = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1],
[1, 1, 0],
[0, 1, 0]])
logits = np.array([[12, 3, 2],
[3, 10, 1],
[1, 2, 5],
[4, 6.5, 1.2],
[3, 6, 1]])
y_pred = sigmoid(logits)
E1 = -y * np.log(y_pred)- (1-y) * np.log(1-y_pred)
print(E1)
sess = tf.Session()
y = np.array(y).astype(np.float64) # labels是float64的資料型別
E2 = sess.run(tf.nn.sigmoid_cross_entropy_with_logits(labels=y,logits=logits))
print(E2)
# output:E1 = E2
[[6.14419348e-06 3.04858735e+00 2.12692801e+00]
[3.04858735e+00 4.53988992e-05 1.31326169e+00]
[1.31326169e+00 2.12692801e+00 6.71534849e-03]
[1.81499279e-02 1.50231016e-03 1.46328247e+00]
[3.04858735e+00 2.47568514e-03 1.31326169e+00]]2.2 softmax 交叉熵損失
softmax交叉熵是最常用的一種損失函數,適用於多分類的問題,在手寫數位識別中每個數位只可能屬於某一個類別。
經softmax層後輸出m維,表示m個類別,這m個值相加等於1,表示屬於某一個類別的概率。
softmax交叉熵損失在tensorflow中定義:
tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)
跟sigmoid交叉熵一樣,這裡的logits都是沒有經過對應的softmax之前的那一層輸出。
如果經過了softmax層,然後再計算交叉熵也是可以的:
# 最後一層的網路輸出result
# 經過一層softmax
result1 = tf.nn.softmax(result)
# 通過result1計算交叉熵
cross_entropy = -tf.reduce_sum(labels * tf.log(result1), 1)上面的方法與softmax_cross_entropy_with_logits得到的結果是一致的。
對於softmax交叉熵,一個樣本所得到的交叉熵就是一個值,一個batch_size的交叉熵就有batch_size個值,因此最後還要進一步加和求loss:
loss = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits, labels))
等價於:
loss = tf.reduce_sum(-tf.reduce_sum(labels * tf.log(result1), 1))
2.3 Sparse 交叉熵損失
Sparse交叉熵損失是用於非ont_hot編碼的標籤,也就是標籤變成了具體的數值,比如對於多分類ont_hot標籤【0,0,1】,那麼Sparse中對應的標籤為數值2。
在tensorflow中處理這樣的問題使用:
tf.nn.sparse_corss_entropy_with_logits(logits, labels)
這個函數會將傳入的非one-hot標籤轉成one-hot標籤,所以它的計算方式與softmax相同,而且適用於多分類的情況,一般情況為了避免不必要的麻煩,不經常使用這個方法,還是直接在處理資料時one-hot。
logits = [[2, 0.5,6],
[0.1,0, 3]]
labels = [2,1]
result = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits)2.4 總結
1、對於二分類情況,通常sigmoid交叉熵和softmax交叉熵損失均可使用,只是使用的方式不同,sigmoid是一個一維的值,softmax是二維的;
2、sigmoid交叉熵損失適用於多標籤分類問題,如一張圖片中既有貓,又有狗;
3、softmax交叉熵損失和Sparse交叉熵損失適用於多分類問題

參考資料:
【深度學習理論】一文搞透sigmoidsoftmax交叉熵/l1/l2/smooth l1 loss
交叉熵和softmax函數和sigmoid函數(在二分類中的比較)
這兩種是深度學習中最常用的損失函數,因此這裡只對這兩種做一個簡單的介紹,主要交叉熵在呼叫的時候容易出錯,這裡做一個記錄。