使用單調棧來解決的一些問題
使用單調棧來解決的一些問題
作者:Grey
原文地址:
單調棧說明
使用單調棧可以實現
陣列中任意一個元素的左邊和右邊離它最近的比它小(大)的數,且時間複雜度
O(N)
先考慮陣列中無重複值的情況,題目描述見:
準備一個棧結構,棧底到棧頂從小到大,陣列中的值依次入棧,入棧條件是:
-
棧為空
-
入棧的元素比棧頂元素大
當不滿足上述兩個入棧條件的情況下,就需要從棧頂彈出元素
彈出的時候,假設彈出的值是 A ,
那麼讓它彈出的值就是 A 右邊離它最近的最小值,
原先 A 壓的是誰,那麼誰就是 A 左邊離它最近的最小值。
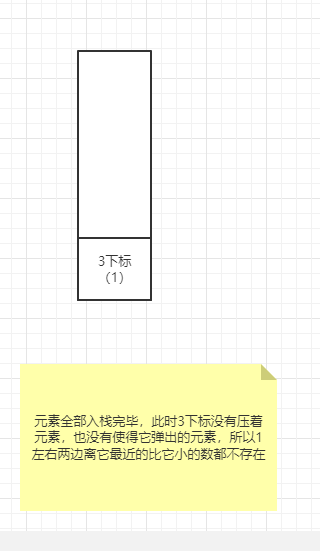
陣列中的元素全部遍歷完,假設棧中還有元素,則棧中元素右側不存在離它最近的比它小的數,左側離它最近比它小的數就是它壓著的數。
注: 棧中存的是陣列下標而非陣列值!
範例圖如下
假設陣列為arr = {5,3,4,1},
棧初始狀態,0號下標直接入棧
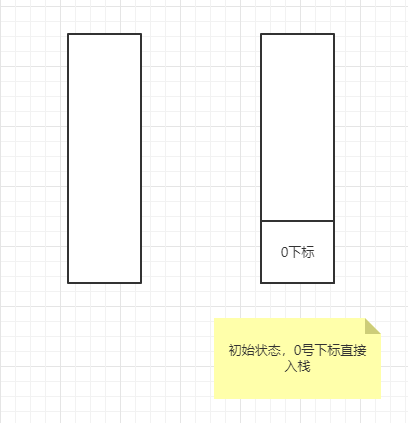
接下來是1號下標準備入棧,因為3 < 5,所以此時棧頂的元素要出棧,由於 5 沒有壓著棧元素,所以 5 左邊離它最近的比它小的數不存在,為-1。5 右邊離它最近的比它小的數就是當前要入棧的 1 下標的 3。
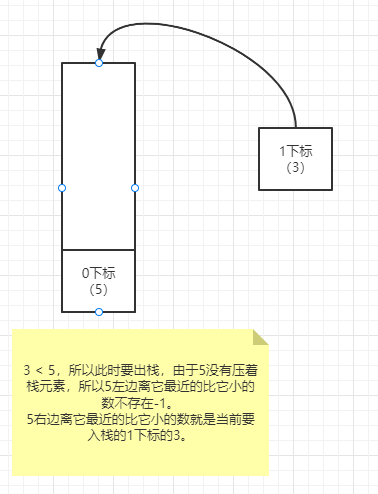
接下來是 2 號下標,滿足入棧條件,直接入棧。
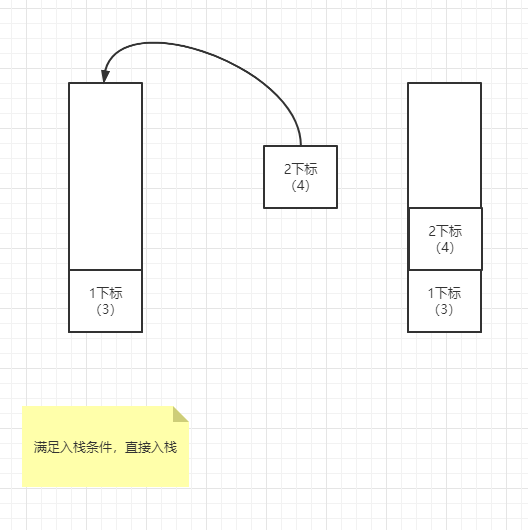
接下來是 3 號下標的 1 準備入棧,由於1 < 4,所以此時要出棧,由於 2 下標壓著 1 下標,所以 4 左邊離它最近的比它小的數是 3。4 右邊離它最近的比它小的數就是當前要入棧的 3 下標的 1。
彈出 2 號下標後,依然滿足出棧條件,同理,棧中 1 號下標的 3 也要彈出。
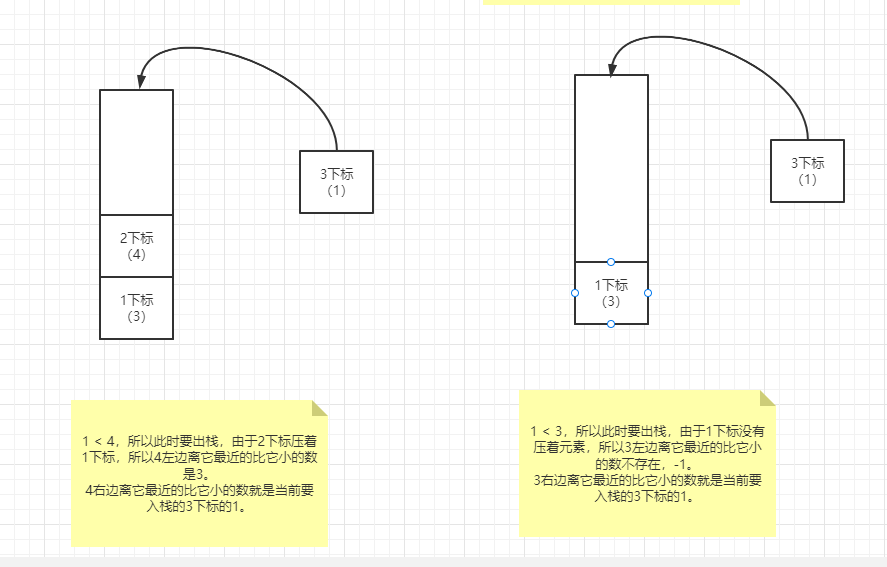
全部遍歷完畢,剩下的元素依次出棧。
完整程式碼如下
// 注:要確保arr中無重複值!
public static int[][] getNearLessNoRepeat(int[] arr) {
int[][] res = new int[arr.length][2];
// 棧底到棧頂從小到大
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
int index = stack.pop();
res[index][0] = stack.isEmpty() ? -1 : stack.peek();
res[index][1] = i;
}
stack.push(i);
}
while (!stack.isEmpty()) {
int index = stack.pop();
res[index][1] = -1;
res[index][0] = stack.isEmpty() ? -1 : stack.peek();
}
return res;
}
在有重複值的情況下,題目描述見牛客:單調棧結構進階(陣列有重複值)
整體流程是一樣的,只是在處理重複值的時候,有一些細微的差別,原先使用的是Stack<Integer>存每個位置左右側離它最近的比它小的數,現在我們改成Stack<List<Integer>>存連續的一批重複值左右側離它最近的比它小的數即可。在彈出棧的過程中,原先是彈出一個,然後結算,現在是彈出一批,同時結算這一批的元素。
完整程式碼如下
public static int[][] getNearLess(int[] arr) {
int[][] result = new int[arr.length][2];
// 重複的元素壓入一批
Stack<List<Integer>> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
List<Integer> selected = stack.pop();
// 原先是結算一個,現在是結算一批
for (int popIndex : selected) {
result[popIndex][0] = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
result[popIndex][1] = i;
}
}
if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {
stack.peek().add(i);
} else {
List<Integer> list = new ArrayList<>();
list.add(i);
stack.add(list);
}
}
while (!stack.isEmpty()) {
List<Integer> list = stack.pop();
for (int popIndex : list) {
result[popIndex][0] = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
result[popIndex][1] = -1;
}
}
return result;
}
類似題目:LeetCode 739. Daily Temperatures
程式碼如下
class Solution {
public static int[] dailyTemperatures(int[] arr) {
if (arr == null || arr.length == 0) {
return new int[]{};
}
int n = arr.length;
int[] ans = new int[n];
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && arr[stack.peek()] < arr[i]) {
int popIndex = stack.pop();
ans[popIndex] = i - popIndex;
}
stack.push(i);
}
// 不需要彈,因為本身初始化就是0,而且棧中的元素本身就沒有右邊離它最近的比它大的數
return ans;
}
}
子陣列累加和乘以子陣列最小值所得到的結果最大是多少
題目描述見:牛客:程式設計題2
暴力方法的主要思路
如果我們列舉必須以陣列某個位置作為最小值的情況下,如何得到最大的結果,那答案必定在其中。
範例陣列如下(為了不混淆,我用字母表示數位)
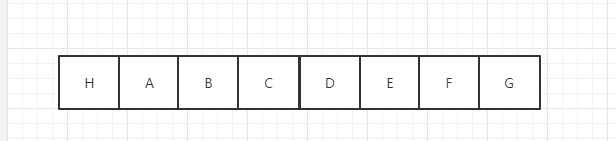
如果列舉
必須以 H 作為最小值,得到的最大結果是多少,假設結果是 HS。
必須以 A 作為最小值,得到的最大結果是多少,假設結果是 AS。
必須以 B 作為最小值,得到的最大結果是多少,假設結果是 BS。
...
必須以 G 作為最小值,得到的最大結果是多少,假設結果是 GS。
那麼 HS,AS,BS ...... GS 中的最大值,就是本題的答案。
所以,本題的暴力解法是
public static int max1(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
for (int j = i; j < arr.length; j++) {
int minNum = Integer.MAX_VALUE;
int sum = 0;
for (int k = i; k <= j; k++) {
sum += arr[k];
minNum = Math.min(minNum, arr[k]);
}
max = Math.max(max, minNum * sum);
}
}
return max;
}
顯然是O(N^3)的時間複雜度。
利用單調棧,本題時間複雜度可以優化為O(N)。
思路如下
首先有一個優化的點:是如何快速得到區間的和?
我們可以通過字首和輔助陣列來加速得到一個區間的和。
第二個關鍵點: 由於需要得到區間的最小值,所以,如果我們得到某個位置左右兩側離它最近的比它小的元素位置在哪裡,就可以定位到:以這個元素為最小值的最大區間和是多少。
範例圖如下,
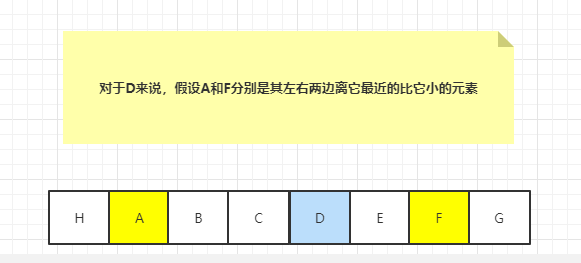
對 D 這個元素來說,如果 A 和 F 是 D 左右兩側比它小的離它最近的元素,那麼以 D 為最小值,可以擴散的最大區間和是 B + C + D + E 的累加和。
而這個就是單調棧可以解決的問題,完整程式碼如下
public static int max2(int[] arr) {
int[] sum = new int[arr.length];
sum[0] = arr[0];
// 字首和陣列優化
for (int i = 1; i < arr.length; i++) {
sum[i] = sum[i - 1] + arr[i];
}
int ans = arr[0] * arr[0];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
int popIndex = stack.pop();
// 結算
ans = Math.max(arr[popIndex] * (sum[i - 1] - (stack.isEmpty() ? 0 : sum[stack.peek()])), ans);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int popIndex = stack.pop();
ans = Math.max(arr[popIndex] * (sum[arr.length - 1] - (stack.isEmpty() ? 0 : sum[stack.peek()])), ans);
}
return ans;
}
LeetCode 有類似的題目『子陣列的最小值之和』
題目描述見:LeetCode 907. Sum of Subarray Minimums
完整程式碼如下
class Solution {
static int MOD = (int) 1e9 + 7;
// arr[i]左右兩邊離i最近的比arr[i]小的位置是m,n
// 必須以arr[i]作為最小值的子陣列有 (i - m) * (n - i)
public static int sumSubarrayMins(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
long max = 0;
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
Integer popIndex = stack.pop();
max += (long) arr[popIndex] * (popIndex - (stack.isEmpty() ? -1 : stack.peek())) * (i - popIndex);
}
stack.push(i);
}
while (!stack.isEmpty()) {
Integer popIndex = stack.pop();
max += (long) arr[popIndex] * (popIndex - (stack.isEmpty() ? -1 : stack.peek())) * (arr.length - popIndex);
}
return (int) (max % MOD);
}
}
直方圖最大矩形的面積
題目描述見:LeetCode 84. Largest Rectangle in Histogram
這一題本質上就是列舉:
必須以arr[i]位置的值為右邊界的最大矩形面積是多少。
如果得到了每個位置的這個指標,最大值就是本題的答案。
而 必須以arr[i]位置的值為右邊界的最大矩形面積是多少。 其實就是在求,arr[i]左側離它最近的比它小的元素在哪?
範例圖
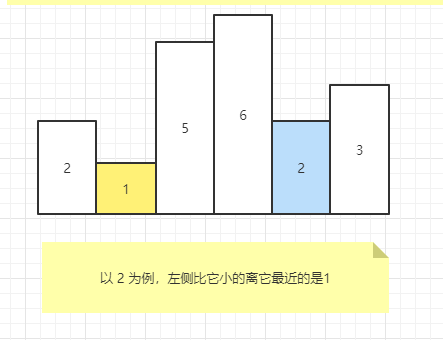
以 2 為例,左側比它小的離它最近的是 1。那麼必須以 2 位置為右邊界的最大矩形如下
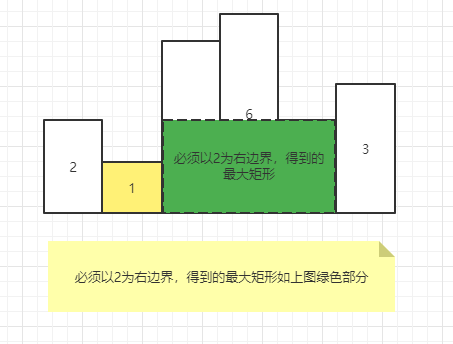
使用單調棧來解,程式碼如下
public static int largestRectangleArea(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int max = arr[0];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
int m = stack.pop();
max = Math.max(max, arr[m] * (i - (stack.isEmpty() ? -1 : stack.peek()) - 1));
}
stack.push(i);
}
while (!stack.isEmpty()) {
int popIndex = stack.pop();
max = Math.max(max, arr[popIndex] * (arr.length - (stack.isEmpty() ? -1 : stack.peek()) - 1));
}
return max;
}
有了這題做鋪墊,那麼 LeetCode 中『找出只包含1的最大矩形的面積』這個問題
題目連結見:LeetCode 85. Maximal Rectangle
也是同樣的思路,只不過,我們需要轉換一下,把二維矩陣轉換成一維陣列,
public static void merge(int[] help, char[] m) {
for (int i = 0; i < help.length; i++) {
help[i] = m[i] == '0' ? 0 : help[i] + 1;
}
}
完整程式碼如下
class Solution {
public static int maximalRectangle(char[][] m) {
int[] help = new int[m[0].length];
int max = 0;
for (int i = 0; i < m.length; i++) {
merge(help, m[i]);
max = Math.max(max, largestRectangleArea(help));
}
return max;
}
public static void merge(int[] help, char[] m) {
for (int i = 0; i < help.length; i++) {
help[i] = m[i] == '0' ? 0 : help[i] + 1;
}
}
public static int largestRectangleArea(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int max = arr[0];
int[] stack = new int[arr.length];
int index = -1;
for (int i = 0; i < arr.length; i++) {
while (index != -1 && arr[stack[index]] >= arr[i]) {
int popIndex = stack[index--];
max = Math.max(max, arr[popIndex] * (i - (index == -1 ? -1 : stack[index]) - 1));
}
stack[++index] = i;
}
while (index != -1) {
int popIndex = stack[index--];
max = Math.max(max, arr[popIndex] * (arr.length - (index == -1 ? -1 : stack[index]) - 1));
}
return max;
}
}
注:對於N * N的矩陣,內部有N^4次方個矩形,所以這題的暴力解法,時間複雜度是O(N^4)。
而採用了單調棧優化後,時間複雜度優化到了O(N^2)。
統計全 1 子矩形個數
題目連結見:LeetCode 1504. Count Submatrices With All Ones
本題的主要思路是:必須以每一行做底的全為 1 的子矩陣是多少,得到每一行的指標後,求和即可;N 為長的矩形一共包含的子矩陣有(N*(N+1)) / 2
由於本題中矩陣中的值不是 0 就是 1, 所以可以借鑑『直方圖最大矩形的面積』的解法
完整程式碼如下:
class Solution {
public int numSubmat(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
int[] help = new int[matrix[0].length];
int count = 0;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (i == 0) {
help[j] = matrix[0][j] == 1 ? 1 : 0;
} else {
help[j] += matrix[i][j] == 1 ? 1 : (-help[j]);
}
}
count += max(help);
}
return count;
}
public static int max(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int nums = 0;
// 用固定陣列來替代Java自帶的棧結果
int[] stack = new int[height.length];
int si = -1;
for (int i = 0; i < height.length; i++) {
// si = -1 說明棧為空
// 棧頂:height[stack[si]]
while (si != -1 && height[stack[si]] >= height[i]) {
int cur = stack[si--];
if (height[cur] > height[i]) {
int left = si == -1 ? -1 : stack[si];
int n = i - left - 1;
int down = Math.max(left == -1 ? 0 : height[left], height[i]);
nums += (height[cur] - down) * num(n);
}
}
// 入棧
stack[++si] = i;
}
while (si != -1) {
int cur = stack[si--];
int left = si == -1 ? -1 : stack[si];
int n = height.length - left - 1;
int down = left == -1 ? 0 : height[left];
nums += (height[cur] - down) * num(n);
}
return nums;
}
public static int num(int n) {
return ((n * (1 + n)) >> 1);
}
}
注:本題使用陣列來替換 Java 中的是 Stack,屬於常規操作,因為 Java 中的 Stack 有一些效能問題,參考:Difference between Deque and Stack
本文所有圖例見:processon:使用單調棧來解決的一些問題
更多
參考資料
本文來自部落格園,作者:Grey Zeng,轉載請註明原文連結:https://www.cnblogs.com/greyzeng/p/16654877.html