【深度學習】——深度學習中基本的網路結構（2）

本節主要複習一下深度學習中這些常見的網路結構在tensorflow（1.x）中的使用，便於後續tensorflow的學習。

1. 全連線網路結構

全連線網路就是後層的每一個神經元均與前一層的神經元有關，按照上一節的推導，zl=w*al-1+b，然後再經過啟用函數記得到了第l層的神經元al：

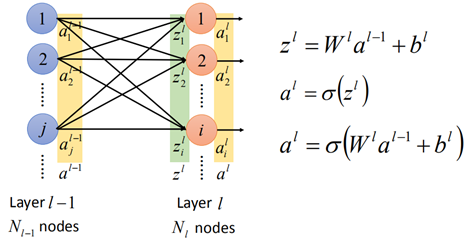
那麼在tensorflow中的實現如下：

# w為權重，b為偏置，x為第l-1層的輸出，這些均為tensor
# 假設x輸入[100]，al-1輸出[10]，事先定義w和b變數
w = tf.Variable(tf.randon_normal([100， 10]))
b = tf.Variable(tf.zeros([10]))
# z = w*x + b
z_l = tf.add(tf.matmal(x, w),  b)
# al = sigmoid(z_l)
a_l = tf.nn.sigmoid(z_l)

這樣就完成了1個全連線層，其中w，b是引數需要事先進行定義。

2. 折積神經網路

折積神經網路在【機器學習】中有一定的介紹，在那邊主要使用的keras進行簡單的實現，這裡結合更多的例子，用tensorflow來進行實現。

首先定義幾個輸入圖片的尺寸：

# shape依次為：batch_size, height, width, channel
inputs = tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 1]))
input2 = tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 2]))
input3 = tf.Variable(tf.constant(1.0, shape=[1, 4, 4, 1]))

然後是filter，有以下幾種filter：

"""
filter的shape依次為：height, width, channel, output_channel
height, width表示filter的大小, channel表示通道數，這個通道數與input的channel是一致的，也就是inputs的第四維，
output_channel為輸出的feature map個數，也就是filter的個數
"""
# 第一個filter 大小2*2，只有1個filter
filter1 = tf.Variable(tf.constant([-1.0, 0, 0, -1], shape=[2, 2, 1, 1]))
# 第二個filter 大小2*2，有2個filter
filter2 = tf.Variable(tf.constant([-1.0, 0, 0, -1, -1, 0, 0, -1], shape=[2, 2, 1, 2]))
# 第三個filter 大小2*2，有3個filter
filter3 = tf.Variable(tf.constant([-1.0, 0, 0, -1, -1, 0, 0, -1, -1, 0, 0, -1], shape=[2, 2, 1, 3]))
# 第四個filter 大小2*2，有2個filter，輸入的channel為2
filter4 = tf.Variable(tf.constant([-1.0, 0, 0, -1.0,
                                   -1.0, 0, 0, -1,
                                   -1.0, 0, 0, -1,
                                   -1.0, 0, 0, -1], shape=[2, 2, 2, 2]))
# 第五個filter，大小2*2，有1個filter，輸入的channel為1
filter5 = tf.Variable(tf.constant([-1.0, 0, 0, -1, -1.0, 0, 0, -1], shape=[2, 2, 2, 1]))

在tensorflow中折積層的定義如下：

tf.nn.conv2d(input, filter, strides, padding, use_cuda_on_gpu)

  input和filter說過了，strides是在折積時在每一維上的步長，也就是1個四維的向量，一般在batch_size和output_channel上都是1。

  padding是否填充邊緣的元素，只能取「SAME」和「VALID」，「SAME」表示邊緣補0，而「VALID」表示不補0，只有當stride為1時，「SAME」才能生成與輸入一致的尺寸。

  關於padding不同取值，決定著輸出圖片尺寸的大小，當為「VALID」情況時：

  

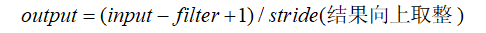
  當padding為「SAME」時，輸出大小與折積核的大小沒有關係，只與stride有關：

  

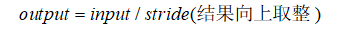
  use_cuda_on_gpu表示是否在gpu上加速，預設為True。

  那麼接下來就根據上面的輸入，根據不同的filter進行折積:

# 輸入5*5*1的圖片，經過1個2*2的filter，步長為2, 那麼輸出為1個3*3的feature map
op1 = tf.nn.conv2d(inputs, filter1, strides=[1, 2, 2, 1], padding="SAME")
# output: shape=(1, 3, 3, 1)

# 輸入5*5*1的圖片，經過2個2*2的filter，步長為2，那麼輸出為2個3*3的feature map
op2 = tf.nn.conv2d(inputs, filter2, strides=[1, 2, 2, 1], padding="SAME")
# output: shape=(1, 3, 3, 2)

# 輸入依舊5*5*1，經過3個2*2的filter，步長為2，輸出則為3個3*3的feature map
op3 = tf.nn.conv2d(inputs, filter3, strides=[1, 2, 2, 1], padding="SAME")
# output： shape=(1, 3, 3, 3)


# 輸入為5*5*1, 但經過filter的channel為2，與輸入的維度不一致，會報錯
op_s = tf.nn.conv2d(inputs, filter4, strides=[1, 2, 2, 1], padding="SAME")
# ValueError: Depth of input (1) is not a multiple of input depth of filter (2) for 'Conv2D_2' (op: 'Conv2D') with input shapes: [1,5,5,1], [2,2,2,2].

# 輸入5*5*2的圖片，有2個channel，經過2個2*2的filter，輸出則為2個3*3的feature map
op4 = tf.nn.conv2d(input2, filter4, strides=[1, 2, 2, 1], padding="SAME")
# output: shape=(1, 3, 3, 2)

# 輸入5*5*2, 經過1個2*2的有2個channel的filter，輸出則為1個3*3的feature map
op5 = tf.nn.conv2d(input2, filter5, strides=[1, 2, 2, 1], padding="SAME")
# output: shape=(1, 3, 3, 1)

# 輸入5*5*1，經過1個2*2的filter，padding=VALID，輸出為（5-2+1）/2=2
v_op1 = tf.nn.conv2d(inputs, filter1, strides=[1, 2, 2, 1], padding="VALID")
# output: shape=(1, 2, 2, 1)

# 輸入4*4*1，經過1個2*2的filter， padding=SAME，輸出為4/2=2
op6 = tf.nn.conv2d(input3, filter1, strides=[1, 2, 2, 1], padding="SAME")
# output: shape=(1, 2, 2, 1)

# 輸入4*4*1，經過1個2*2的filter， padding=VALID，輸出為(4-2+1)/2=2
v_op6 = tf.nn.conv2d(input3, filter1, strides=[1, 2, 2, 1], padding="VALID")
# output: shape=(1, 2, 2, 1)

  折積之後一般還有池化，下面是池化的方法：

tf.nn.max_pool(input, ksize, strides, padding, name)
tf.nn.avg_pool(input, ksize, strides, padding, name)

  input是輸入，ksize跟折積中的filter一樣，這裡需要注意的是，第一維和第四維一般為1，因為一般不在batch和channel上做池化，輸出channel一般與輸出一致。其它與折積中的引數一致。

  下面舉個例子，輸入圖片為：

img = tf.constant([[[0.0, 4.0], [0.0, 4.0], [0.0, 4.0], [0.0, 4.0]],
                   [[1.0, 5.0], [1.0, 5.0], [1.0, 5.0], [1.0, 5.0]],
                   [[2.0, 6.0], [2.0, 6.0], [2.0, 6.0], [2.0, 6.0]],
                   [[3.0, 7.0], [3.0, 7.0], [3.0, 7.0], [3.0, 7.0]]])


img = tf.reshape(img, [1, 4, 4, 2])

# 輸入均為4*4*2
# filter大小為2*2，步長為2，輸出為(4-2+1)/2=2，輸出channel依舊是2
pooling1 = tf.nn.max_pool(img, [1, 2, 2, 1], [1, 2, 2, 1], padding='VALID')
# output: shape=(1, 2, 2, 2)

# filter大小為2*2，步長為1，輸出為(4-2+1)/1=3，輸出channel依舊為2
pooling2 = tf.nn.max_pool(img, [1, 2, 2, 1], [1, 1, 1, 1], padding='VALID')
# output: shape=(1, 3, 3, 2)

# avg_pool跟max_pool類似，filter大小4*4，步長1，"SAME"與折積核無關，輸出為4/1=4
pooling3 = tf.nn.avg_pool(img, [1, 4, 4, 1], [1, 1, 1, 1], padding='SAME')
# output: shape=(1, 4, 4, 2)

# filter4*4，步長為4，"SAME"與折積核無關，輸出為4/4=1
pooling4 = tf.nn.avg_pool(img, [1, 4, 4, 1], [1, 4, 4, 1], padding='SAME')
# output: shape=(1, 1, 1, 2)

   此外還有反折積操作和反池化操作，首先是反折積，在【機器學習基礎】中說過，其實反折積就是一種折積，不過是在邊緣補0之後再進行折積，在tensorflow中有函數來實現：

tf.nn.conv2d_transpose(input, filter, output_shape, strides, padding)

  input表示輸入；

  filter是指在原圖在折積時所使用的filter；

  output_shape反折積後的尺寸大小，也就是原圖經過折積前的尺寸；

  strides表示原圖經過折積時的strides；

  padding表示原圖在折積時使用的padding

  下面是範例：

# 原圖片，並經過折積
img = tf.Variable(tf.constant(1.0, shape=[1, 4, 4, 1]))
filter = tf.Variable(tf.constant([1.0, 0, -1, -2], shape=[2, 2, 1, 1]))

conv = tf.nn.conv2d(img, filter, strides=[1, 2, 2, 1], padding='VALID')
cons = tf.nn.conv2d(img, filter, strides=[1, 2, 2, 1], padding='SAME')

# 反折積過程,所有引數與折積過程保持一致,輸出則為img的尺寸
contv = tf.nn.conv2d_transpose(conv, filter, [1, 4, 4, 1], strides=[1, 2, 2, 1], padding="VALID")
conts = tf.nn.conv2d_transpose(cons, filter, [1, 4, 4, 1], strides=[1, 2, 2, 1], padding="SAME")

  然後接下來是反池化，在【機器學習】基礎中，反池化的原理也已經過了，這裡就不再贅述。

  這裡直說實現，對於反池化的操作，有一點比較麻煩的在池化過程中，我們要知道哪一個元素被選為最大，在反池化時，要將對應的元素還原，其他元素置為0。因此，池化時還需要記錄被選中的那一個元素。

  因此，這裡需要對池化操作重新寫，tensorflow中提供了記錄最大值的方法tf.nn.max_pool_with_argmax方法，下面是修改後的池化操作，放在這裡後面可以直接用：

# 返回值是池化後的網路以及對應的索引值
def max_pool_with_argmax(net, stride):
    _, mask = tf.nn.max_pool_with_argmax(net, ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1], padding='SAME')
    mask = tf.stop_gradient(mask)
    net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1], padding='SAME')
    return net, mask

  有了返回的索引，就可以進行反池化操作了，反池化沒有現成的函數，需要自己實現，下面是實現過程，記下便於後續使用：

def unpool(net, mask, stride):
    ksize = [1, stride, stride, 1]
    input_shape = net.get_shape().as_list()

    # 計算new_shape
    output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2]*ksize[2], input_shape[3])
    one_like_mask = tf.ones_like(mask)
    batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1])
    b = one_like_mask * batch_range
    y = mask // (output_shape[2] * output_shape[3])
    x = mask % (output_shape[2] * output_shape[3]) // output_shape[3]
    feature_range = tf.range(output_shape[3], dtype=tf.int64)
    f = one_like_mask * feature_range

    update_size = tf.size(net)
    indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, update_size]))
    values = tf.reshape(net, [update_size])
    ret = tf.scatter_nd(indices, values, output_shape)
    return ret

  下面舉個例子來進行池化和反池化操作：

img = tf.constant([[[0.0, 4.0], [0.0, 4.0], [0.0, 4.0], [0.0, 4.0]],
                   [[1.0, 5.0], [1.0, 5.0], [1.0, 5.0], [1.0, 5.0]],
                   [[2.0, 6.0], [2.0, 6.0], [2.0, 6.0], [2.0, 6.0]],
                   [[3.0, 7.0], [3.0, 7.0], [3.0, 7.0], [3.0, 7.0]]])
img = tf.reshape(img, [1, 4, 4, 2])

# 池化操作，stride=2，一般在max_pool時設定步長與stride一致
pool, mask = max_pool_with_argmax(img, 2)

# 反池化
img2 = unpool(pool, mask, 2)

with tf.Session() as sess:
    print('img', img)

    result = sess.run(img2)
    print('img2', result)
    

  可以看到img2和img在尺寸上是一致的，但是數值不太一樣，這在前面說過，對與不是最大值的部分填充0。

  有了上面的基本結構，就可以構建一個簡單的CNN深度網路了，下面是是一個基本的網路結構範例：

# 先定義初始化引數的函數，不必每次遇到引數定義就初始化一次，直接呼叫
def weight_variable(shape):
    initial = tf.Variable(tf.truncated_normal(shape, std=0.1))
    return initial

# 同樣定義bias
def bias_variable(shape):
    initial = tf.Variable(tf.constant(0.1, shape=shape))
    return initial

# 定義折積函數，每次直接呼叫即可
def conv2d(x, w):
    return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding="SAME")

# 輸入預留位置，圖片大小24*24*3
x = tf.placeholder(tf.float32, [batch_size, 24, 24, 3])
# 輸出預留位置，10個類別
y = tf.placeholder(tf.float32, [batch_size, 10])

# 第一個折積層的折積核引數，有64個5*5*3的filter
w_conv1 = weight_variable([5, 5, 3, 64])
# 折積後需要加上一個bias, 折積後為64個feature map，所以bias維度為64
b_conv1 = bias_variable([64])
# 折積操作，一般折積層後會接RELU,輸出的尺寸為24/1=24，channel為64
h_conv1 = tf.relu(conv2d(x, w_conv1) + b_conv1)
# 然後是池化操作,池化後尺寸為12*12*64
h_pool1, mask1 = max_pool_with_argmax(h_conv1, 2)

# 第二層折積的折積核引數，有64個5*5*64的
w_conv2 = weight_varibale([5, 5, 64, 64])
b_conv2 = bias_varibale([64])
# 第二次折積操作，折積後依舊12*12*64
h_conv2 = tf.relu(conv2d(h_pool1, w_conv2) + b_conv2)
# 第二次池化，池化後尺寸6*6*64
h_pool2, mask2 = max_pool_with_argmax(h_conv2, 2)

# 接下來反池化操作，對h_pool2進行反池化，得到第二次折積後的結果
t_conv2 = unpool(h_pool2, mask2, 2)
# 然後是反折積，反折積後，與第一次池化結果對應
# 反折積操作中要減掉bias
t_pool1 = tf.nn.conv2d_transpose(t_conv2 - b_conv2, w_conv2, h_pool1.shape, [1, 1, 1, 1])

# 再次反池化，返回到第一次折積後的結果
t_conv1 = unpool(t_pool1, mask1, 2)
# 再次反折積，反折積後即回到初始的x
t_x = tf.nn.conv2d_transpose(t_conv1 - b_conv1, w_conv1, x.shape, [1, 1, 1, 1])

# 緊接著在第二次池化後，在進行一次折積池化操作
w_conv3 = weight_varibale([5, 5, 64, 10])
b_conv3 = bias_variable([10])
# 第三次折積後的輸出為6*6，channel為10
h_conv3 = tf.nn.relu(conv2d(h_pool2, w) + b_conv3)
# 最後經過一個6*6的avg_pool,輸出為1*1，channel為10
h_pool3 = tf.nn.avg_pool(h_conv3, [1, 6, 6, 1], strides=[1, 6, 6, 1], padding="SAME")

# 將h_pool3展開，輸入到softmax
h_pool3_flat = tf.reshape(h_pool3, [-1, 10])

# 可以再接幾層fc
fc1 = tf.layers.dense(h_pool3_flat, 64, activation=tf.nn.tanh)
fc2 = tf.layers.dense(fc1, 64, activation=tf.nn.tanh)

y_pred = tf.layers.dense(fc2, 10, activation=tf.nn.softmax)

  這樣，一個三層的折積神經網路就好了，在折積後的三層其實可以再接幾層fc層。

  以上就是一個較為完整的網路的實現了。

  這裡需要注意：反折積和反池化的作用主要是為了實現視覺化、或者還原原影象解析度的問題，並沒有參與訓練。

  另外，關於折積後需要加bias的問題，當折積後接Bath Normalization（後面會說）時，是不需要加bias的。

3. RNN

  RNN中有多種結構，除了基本的basic RNN，還有LSTM、GRU。在使用RNN時，需要預先定義好cell，然後再將cell連線起來，構成RNN網路。

  tensorflow中包含了上面幾種cell的定義：

3.1basic RNN

  首先是basic RNN，該cell的定義如下：

tf.contrib.rnn.BasicRNNCell(num_units, input_size=None, activation=tanh)

  num_units表示隱藏節點的個數，也就是ht的維度，input_size廢棄了不再使用。

  定義一個basic RNN cell也比較簡單，只需指定好n_hidden的大小即可：

  basic_rnn_cell = tf.contrib.rnn.BasicRNNCell(n_hidden)

3.2 LSTM

  然後是LSTM，也是類似，LSTM定義為：

tf.contrib.rnn.BasicLSTMCell(num_units, forget_bias=1.0, state_in_tuple, activation)

  num_units一樣表示隱藏層節點的個數，forget_bias是新增到遺忘門的偏置，表示保留多少資訊，預設為1。

  state_in_tuple是否將記憶c和h以tuple的形式分開，當為True時輸出tuple(c=array(), h=array())，當為False時兩個連線起來[batch, 2n]，該引數即將廢棄。

  定義一個basic LSTMcell：

  basic_lstm = tf.contrib.rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)

  這樣就定義好了一個基本的LSTM結構。

  還有另一個LSTM的高階版本版本，除了上面的引數外，還有一些其他的引數：

 

 

 

 

 

3.3 GRU

  GRU的定義也是一樣的：

tf.contrib.rnn.GRUCell(num_units, input_size=None, activation=tanh)

  basic_gru = tf.contrib.rnn.GRUCell(n_hidden)

3.4 MultiRNN

  上面就是幾個基本cell的定義，當然，cell不單單是某一種，可以是多種組合起來的多層cell，其定義：

tf.contrib.rnn.MultiRNNCell(cells, state_in_tuple)

  cells就是一個cell的列表，該列表為一系列basic cell組成，cells=[cell1, cell2]就表示有兩層資料經過cell1後還要經過cell2.

  state_in_tuple於basic rnn中類似，將記憶cell與隱藏狀態輸出h組成一個tuple。

  注意：在使用MultiCell時，cells不能直接用[cell]×n的寫法，如果不使用作用域會報錯，而是要用append的寫法。

  建立一個多層的cell：

cell1 = tf.contrib.rnn.BasicLSTMCell(n_hidden)
cell2 = tf.contrib.rnn.GRUCell(n_hidden)
#如果兩個cell的n_hidden,則輸出以最後一個節點為準
multi_rnn = tf.contrib.rnn.MultiRNNCell([cell1, cell2])

 3.5 RNN的連線

  上面構建出基本的RNN cell時只是某一個時刻的狀態，接下來還要把Cell連線起來，才能構成完整的RNN網路。

  RNN的連線方式可以分為靜態、動態，單向RNN和雙向RNN，再結合上面的單層的cell和多層的cell，那麼RNN各種條件自由組合，可以有8中不同的連線。

  這裡所謂的靜態和動態，是指在建立RNN時，RNN預先建立好的結構，這時需要輸入的長度要與該結構保持一致；

  因此靜態的因為預先建立好，會花費較多的時間和佔用空間，但其優點是可以檢視任一時刻的輸出，便於偵錯；

  而動態則是指比較靈活地根據輸入去建立cell，通過迴圈來建立的。

  因此動態的建立快，節省記憶體，便於不同長度的輸入的批次處理，但缺點是隻能檢視序列最終狀態，不方便偵錯。

  靜態的建立方式：

  tf.contrib.rnn.static_rnn(cells, input, initial_state=None, sequence_length=None, scope=None)

  cells為前面說的cell；

  input為輸入；

  initial_state初始化狀態引數，一般初始化為0時，不需刻意指定，要是想要初始化指定的值用initial_state=LSTMStateTuple(c_state, h_state)

  sequence_lenght一般不需要指定，會根據輸入自動識別；

  scope：名稱空間。

  動態的建立方式：

  tf.contrib.rnn.dynamic_rnn(cells, input, initial_state=None, sequence_length=None, time_major, scope=None)

  引數基本與靜態的一致，這裡多了一個time_major，預設為False時，input_shape=[batch_size, max_time, .....], 當為True時，input_shape=[max_time, batch_size, ....]

  接下來就是各種RNN的實現方式：

3.5.1 單向的RNN：

  ① 單層靜態單向RNN

# 輸入x為n_step*n_input,即n_step個時間點，每個時間點的維度為n_input
x = tf.placeholder(tf.float32, [None, n_steps, n_input])

# 先建立一個lstm cell
lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden)
# 靜態單層RNN
# 需要先轉換x的形狀為預設形狀
x1 = tf.unstack(x, n_steps, 1)

outputs, states = tf.contrib.rnn.static_rnn(lstm_cell, x1, dtype=tf.float32)
# outputs包括結果和cell的狀態，只需關注結果，最後一維才是結果
pred = tf.contrib.layers.fully_connected(couputs[-1], 10, activation_fn=None)

  ②多層靜態單向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])

# 先建立多層的cells
cells = []
for i in range(3):
    cells.append(tf.contrib.rnn.BasicLSTMCell(n_hidden))
    
multi_cell = tf.contrib.rnn.MultiRNN(cells)

x1 = tf.unstack(x, n_steps, 1)
# 多層靜態單向RNN
outputs, states = tf.contrib.rnn.static_rnn(multi_cell, x1, dtype=tf.float32)

pred = tf.contrib.layers.fully_connected(outputs[-1], 10, activation_fn=None)

  ③單層動態單向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])

# 先建立basic cell
lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden)

# 動態單層單向RNN
outputs, state = tf.contrib.rnn.dynamic_rnn(lstm_cell, x, dtype=tf.float32)

outputs = tf.transpose(outputs, [1, 0, 2])

pred = tf.contrib.layers.fully_connected(outputs[-1], 10, activation_fn=None)

   ④多層動態單向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])
# basic cell
lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden*2)

gru_cell = tf.contrib.rnn.GRUCell(n_hidden)
# 構建多層cell
multi_cells = tf.contrib.rnn.MultiRNNCell([lstm_cell, gru_cell])

# 多層動態單向RNN
outputs, state = tf.contrib.rnn.dynamic_rnn(multi_cells, x, dtype=tf.float32)

outputs = tf.transpose(outputs, [1, 0, 2])

pred = tf.contrib.layers.fully_connected(outputs[-1], 10, activation_fn=None)

  從上面的程式碼可以看到，靜態和動態的區別再輸入和輸出的格式轉化，主要有兩點：

  1、靜態的輸入需要將輸入轉換成list的形式，而動態網路不需要轉換。這是因為靜態是預先設定好的，必須按照設定的輸入；

  2、動態的輸出需要進行轉置操作，而靜態的則不需要。這是因為動態網路輸出形式為[batch_size, max_time, ...]，

     轉置[1, 0, 2]是將第0維max_time放在後面，將batch_size放在第1維，這樣轉換後變為[max_time, batch_size,.....], 取最後一維時就是最後一個時間點的資料[batch_size, ......]

3.5.2 雙向的RNN

  雙向的RNN在單層和多層之間的定義還是有所差別的，對於單層的CELL的靜態RNN定義：

  tf.contrib.rnn.static_bidirectional_rnn(cell_fw, cell_bw, inputs)

  對於單層的動態RNN定義如下：

  tf.nn.bidirectional_dynamic_rnn(cell_fw, cell_bw, inputs)

  而對於多層的靜態RNN定義：

  tf.contrib.rnn.stack_bidirectional_rnn(cells_fw, cells_bw, inputs)

  對於多層動態的RNN定義：

  tf.contrib.rnn.stack_bidirectional_dynamic_rnn(cells_fw, cells_bw, inputs)

  從上面的四個定義可以看出：

  無論是單層還是多層，均需一個前向的cell和一個反向的cell，且前向的cell和反向的cell的結構必須保持一致；  

  對於單層的定義沒有「stack」，多層的需要帶「stack」，其中單層動態的來自於tf.nn模組；

  而對於多層的cells可以接受列表的形式，也可以接受Multi形式的cell，後面舉例說明。

  ① 單層靜態雙向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])
# 對於靜態的而言，輸入要調整為list
x1 = tf.unstack(x, n_stpes, 1)
# 先建立basic cell，前向和反向
cell_fw = tf.contrib.rnn.BasicLSTMCell(n_hidden)
cell_bw = tf.contrib.rnn.GRUCell(n_hidden)

# 單層靜態雙向RNN
outputs, _, _ = tf.contrib.rnn.static_bidirectional_rnn(cell_fw, cell_bw, x1)

pred = tf.contrib.layers.fully_connected(outputs[-1], 10, activation_fn=None)

  ②單層動態雙向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])

cell_fw = tf.contrib.rnn.BasicLSTMCell(n_hidden)
cell_bw = tf.contrib.rnn.GRUCell(n_hidden)

outputs, _, _ = tf.nn.bidirectional_dynamic_rnn(cell_fw, cell_bw, x, dtype=tf.float32)

# 動態rnn的輸出需要進行轉化為[max_time, batch_size, ....]
outputs = tf.transpose(outputs, [1, 0, 2])

pred = tf.contrin.layers.fully_connected(outputs[-1], 10, activation_fn=None)

  ③多層靜態雙向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])

x1 = tf.unstack(x, n_steps, 1)

cell_fw = tf.contrib.rnn.BasicLSTMCell(n_hidden)
cell_bw = tf.contrib.rnn.GRUCell(n_hidden)

# 建立多層靜態雙向RNN，多層的只需將cell放入列表即可，但必須保證前向與後向結構一致
outputs, _, _ = tf.contrib.rnn.stack_bidirectional_rnn([cell_fw], [cell_bw], x1, dtype=tf.float32)

pred = tf.contrib.layers.fully_connected(outputs[-1], 10, activation_fn=None)

# 多層的也接受multi cell
stack_cells_fw = []
stack_cells_bw = []
for i in range(3):
    stack_cells_fw.append(tf.contrib.rnn.BasicLSTMCell(n_hidden))
    stack_cells_bw.append(tf.contrib.rnn.BasicLSTMCell(n_hidden))
    
multi_cells_fw = tf.contrib.rnn.MultiRNNCell(stack_cells_fw)
multi_cells_bw = tf.contrib.rnn.MultiRNNCell(stack_cells_bw)

outputs, _, _ = tf.contrib.rnn.stack_bidirectional_rnn([multi_cells_fw], [multi_cells_bw], x1, dtype=tf.float32)
......

   ④多層動態雙向RNN

x = tf.placeholder(tf.float32, [None, n_steps, n_input])

stack_cells_fw = []
stack_cells_bw = []

for i in range(3):
    stack_cells_fw.append(tf.contrib.rnn.BasicLSTMCell(n_hidden))
    stack_cells_bw.append(tf.contrib.rnn.BasicLSTMCell(n_hidden))
    
# 多層動態雙向RNN

outputs, _, _ = tf.contrib.rnn.stack_bidirectional_dynamic_rnn(stack_cells_fw, stack_cells_bw, x, dtype=tf.float32)

outputs = tf.transpose(outputs, [1, 0, 2])

pred = tf.contrib.layers.fully_connected(outputs[-1], 10, activation_fn=None)

# 也接受Multi cell
multi_cells_fw = tf.contrib.rnn.MultiRNNCell(stack_cells_fw)
multi_cells_bw = tf.contrib.rnn.MultiRNNCell(stack_cells_bw)

outputs, _, _ = tf.contrib.rnn.stack_bidirectional_dynamic_rnn([multi_cells_fw], [multi_cells_bw], x, dtype=tf.float32)
......

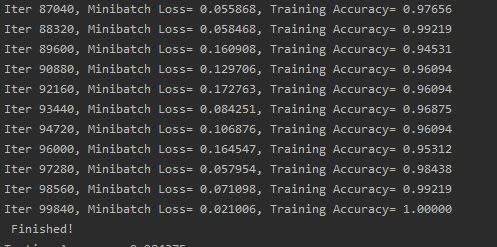
   以上就是RNN的基本結構的實現過程，下面利用MNIST資料集，使用RNN訓練一個模型：

import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data


# 讀取資料
mnist = input_data.read_data_sets("/data/", ont_hot=True)

# 引數設定
learning_rate = 0.001
traning_iters = 100000
batch_size = 128
display_step = 10

# 網路的引數
# 圖片尺寸28*28，當做序列長度為28，每一個時刻的維度為28
n_inputs = 28 # 每一個序列的維度
n_steps = 28 # 序列長度
n_hidden = 128 # 隱藏層的輸出維度
n_classes = 10 # 0~9 10個類別

# 初始化圖
tf.reset_default_graph()

# 輸入、輸出的預留位置
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes])

# 這裡採用多層雙向動態RNN
# 定義前向、後向basic cells
stack_cells_fw = []
stack_cells_bw = []
for i in range(3):
    stack_cells_fw.append(rnn.BasicLSTMCell(n_hidden))
    stack_cells_bw.append(rnn.GURCell(n_hidden))
    
# 轉為multi_cells
multi_cells_fw = rnn.MultiRNNCell(stack_cells_fw)
multi_cells_bw = rnn.MultiRNNCell(stack_cells_bw)

# 建立多層雙向動態RNN
outputs, _, _ = rnn.stack_bidirectional_dynamic_rnn([multi_cells_fw], [multi_cells_bw], x, dtype=tf.float32)

outputs = tf.transpose(outputs, [1, 0, 2])

# 輸出值後接一個全連線網路，輸出為10維，classes
pred = tf.contrib.layers.fully_connected(outputs[-1], n_classes, activation_fn=None)

# 計算loss,採用cross_entropy
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))

# 梯度下降
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(loss)

# 估計正確率
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(corrected_pred, tf.float32))

# 啟動session開始訓練
with tf.Session() as sess:
    # 初始化
    sess.run(tf.global_variables_initializer())
    step = 1
    while step * batch_size < training_iters:
        # 批資料
        batch_x, batch_y = mnist.train.next_batch(batch_size)
        # 將batch_x 轉成x的形狀
        batch_x = batch_x.reshape([batch_size, n_steps, n_input])
        
        sess.run(optimizer, feed_dict={x:batch_x, y: batch_y})
        # 列印訓練過程
        if step%display_step == 0:
            # 計算這一輪的精度
            acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
            # 計算損失
            cost = sess.run(loss, feed_dict={x: batch_x, y: batch_y})
            print('Iter' + str(step * batch_size) + ', Mini-batch loss= ', + '{:.6f}'.format(cost) + ', Training Accuracy=' + '{:.5f}'.format(acc))
        step += 1
    print('Finished')

    # 計算在測試集上的準確率
    test_len = 128
    test_data = mnist.test.images[:test_len].reshape([-1, n_steps, n_input])
    test_labels = mnist.test.labels[:test_len]
    print('Testing Accuracy：', sess.run(acc, feed_dict={x: test_data, y: test_labels}))