前端也該刷點演演算法題——雙指標解「連結串列」題也太香了叭!
2022-08-31 21:00:23
雙指標解「連結串列」題也太香了叭!
同步雙指標
1 查詢連結串列中倒數第 k 個節點
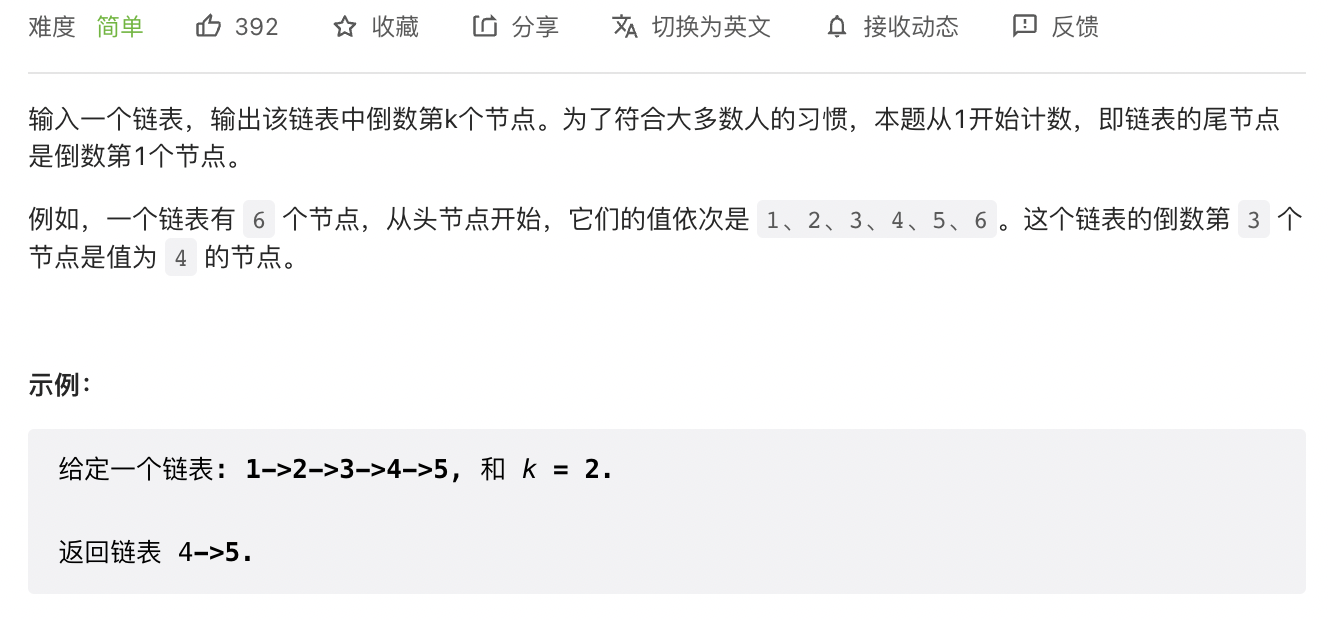
思路:
-
假設連結串列的長度為
n,不難得出倒數第k個節點即為整數第n + 1 - k。 -
如果一個指標從頭節點開始走
k步(頭節點算作第1步),則還需n + 1 - k步才能走完連結串列(到達尾節點的next,即 null)。 -
我們用雙指標,一個指標先走
k步,然後兩個指標同時走n + 1 - k步,其中一個指標走完連結串列,另一個指標走到第n + 1 - k個節點處,即倒數第k個節點
程式碼
JS
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @param {number} k
* @return {ListNode}
*/
var getKthFromEnd = function (head, k) {
let p1 = head;
// 注意此處 i < k - 1,因為 p1 賦值時算作第 1 步
for (let i = 0; i < k - 1; i++) {
p1 = p1.next;
}
let p2 = head;
p1 = p1.next; // 同理 p2 賦值算作第 1 步,所以 p1 也要走 1 步
while (p1) {
p1 = p1.next;
p2 = p2.next;
}
return p2;
};
// 時間複雜度 O(n) n為連結串列長度
// 空間複雜度 O(1)
TS
/**
* Definition for singly-linked list.
* class ListNode {
* val: number
* next: ListNode | null
* constructor(val?: number, next?: ListNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
* }
*/
function getKthFromEnd(head: ListNode | null, k: number): ListNode | null {
const dummyHead = new ListNode();
dummyHead.next = head;
let p1 = dummyHead;
for (let i = 0; i < k; i++) {
p1 = p1.next;
}
let p2 = dummyHead;
while (p1) {
p1 = p1.next;
p2 = p2.next;
}
return p2;
}
// 時間複雜度 O(n) n為連結串列長度
// 空間複雜度 O(1)
注:JS 和 TS 的實現略微有些不同,TS 中新增了一個虛擬頭節點,虛擬頭節點在解決連結串列相關的一些題目時非常有用,體會一下不用虛擬頭節點和使用虛擬頭節點的差別
2 刪除連結串列中倒數第 k 個節點
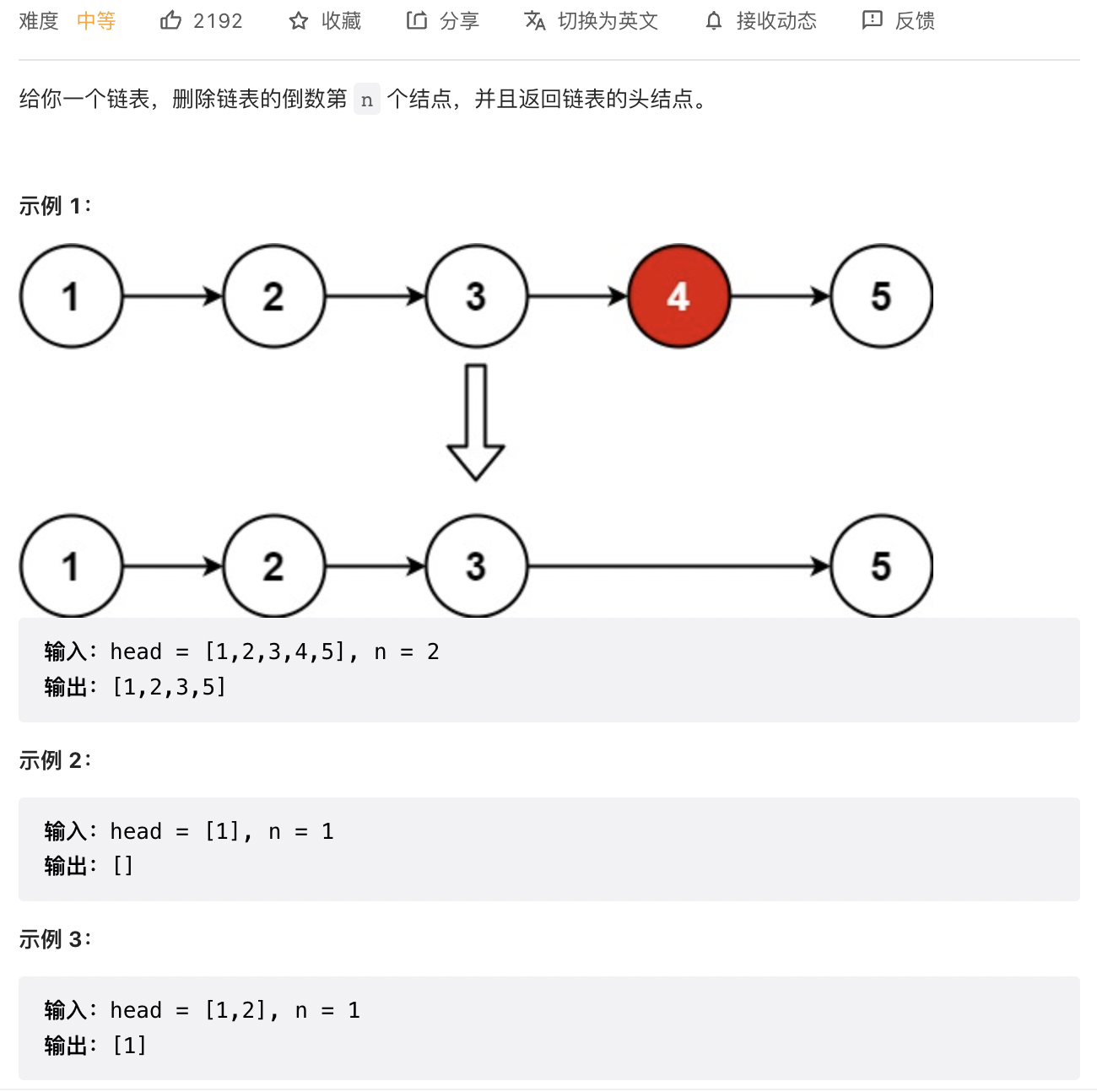
思路
-
刪除和查詢倒數第 k 個節點的思路大致相同
-
唯一的區別是刪除倒數第 k 個節點時我們應該查詢倒數第 k + 1 個節點,然後讓其 next 指向 next 的 next。
因為我們要查詢倒數第 k + 1 個節點,所以應該讓第一個指標先走 k + 1 步
-
此外刪除的有可能是第 1 個節點,見範例2,此時刪除的是倒數第 1 個節點,所以我們要查詢倒數第 2 個節點,然而連結串列總共才 1 個節點,因此我們引入虛擬頭節點來解決
程式碼
JS
var removeNthFromEnd = function (head, n) {
const dummyHead = new ListNode();
dummyHead.next = head; // 將虛擬頭節點接入連結串列
let p1 = dummyHead;
// p1 先走 n + 1 步
for (let i = 0; i < n + 1; i++) {
p1 = p1.next;
}
let p2 = dummyHead;
while (p1) {
p1 = p1.next;
p2 = p2.next;
}
p2.next = p2.next.next;
// 注意不是返回 head,因為 head 有可能被刪除
return dummyHead.next;
};
// 時間複雜度 O(n) n為連結串列長度
// 空間複雜度 O(1)
TS
function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
const dummyHead = new ListNode();
dummyHead.next = head;
let p1 = dummyHead;
for (let i = 0; i < n + 1; i++) {
p1 = p1.next;
}
let p2 = dummyHead;
while (p1) {
p1 = p1.next;
p2 = p2.next;
}
p2.next = p2.next.next;
return dummyHead.next;
}
注:嘗試不用虛擬頭節點解此題,體會虛擬頭節點的妙處
3 查詢兩條連結串列的相交節點
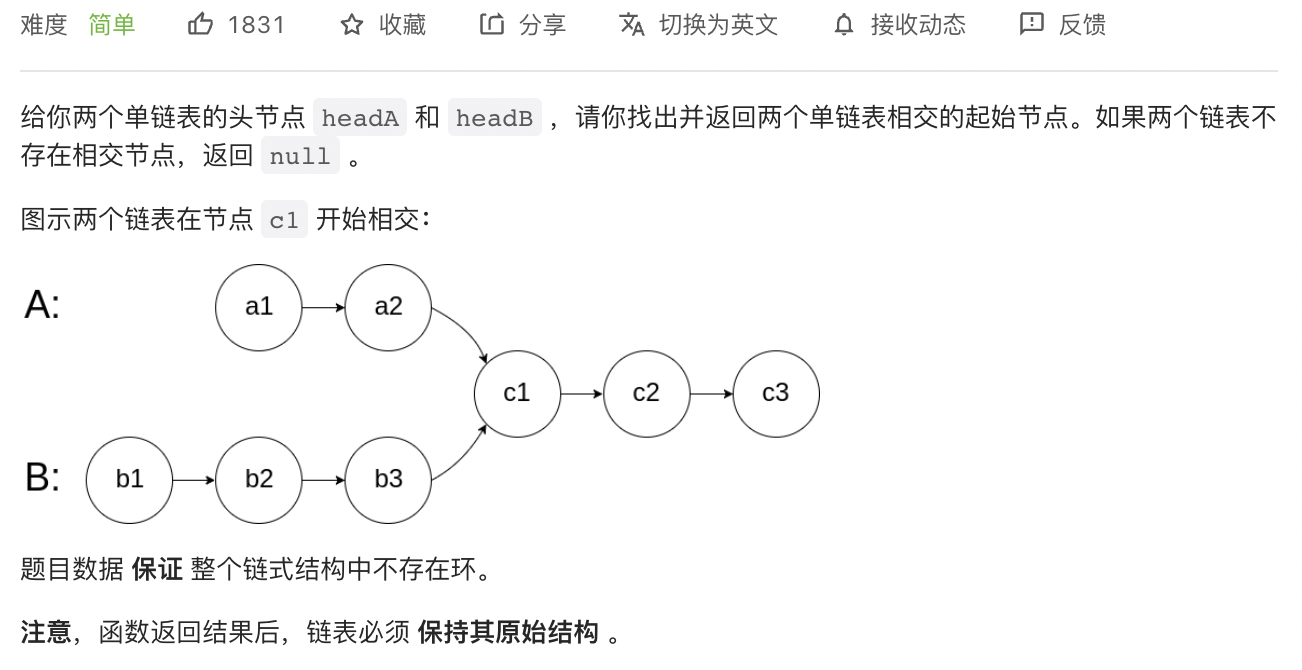
思路
- 雙指標 p1 和 p2 分別從 headA 和 headB 出發
- 如果 p1 走完了連結串列 A,就從 headB 接著走;同理,如果 p2 走完了連結串列 B,就從 headA 接著走
- 在這種走法下,p1 和 p2 一定同時走完
- 如果兩條連結串列相交,那麼 p1 和 p2 一定會在交點相遇,因為從交點開始到結束點,兩條連結串列的路徑是相同的,於是 p1 和 p2 從結束點向前推能同時到達交點
- 如果兩條連結串列不相交,則 p1 和 p2 全程不會相遇
程式碼
JS
var getIntersectionNode = function (headA, headB) {
let p1 = headA;
let p2 = headB;
while (p1 || p2) {
if (p1 === p2) return p1;
p1 = p1 ? p1.next : headB;
p2 = p2 ? p2.next : headA;
}
return null;
};
// 時間複雜度 O(n + m) m、n 分別為兩條連結串列長度
// 空間複雜度 O(1)
TS
function getIntersectionNode(
headA: ListNode | null,
headB: ListNode | null
): ListNode | null {
let p1 = headA;
let p2 = headB;
while (p1 || p2) {
if (p1 === p2) return p1;
p1 = p1 ? p1.next : headB;
p2 = p2 ? p2.next : headA;
}
return null;
}
快慢雙指標
1 查詢連結串列的中間節點

思路
- 這題我們讓兩個指標同時走,不過兩個指標的速度不同,分為快慢指標
- 我們讓慢指標每次走 1 步,快指標每次走 2 步
- 當快指標走完連結串列,即指向 null,慢指標就走到了中間節點的位置
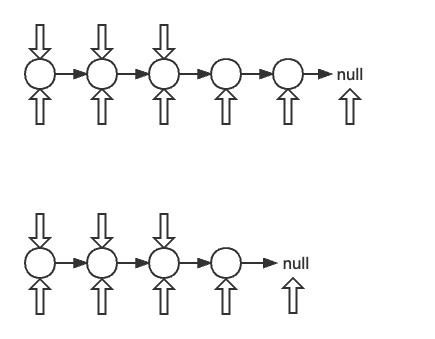
程式碼
JS
var middleNode = function (head) {
const dummyHead = new ListNode();
dummyHead.next = head;
let fastP = dummyHead;
let slowP = dummyHead;
while (fastP) {
slowP = slowP.next;
fastP = fastP.next;
fastP && (fastP = fastP.next);
}
return slowP;
};
// 時間複雜度 O(n) n 為連結串列長度
// 空間複雜度 O(1)
TS
function middleNode(head: ListNode | null): ListNode | null {
const dummyHead = new ListNode();
dummyHead.next = head;
let fastP = dummyHead;
let slowP = dummyHead;
while (fastP) {
slowP = slowP.next;
fastP = fastP.next;
fastP && (fastP = fastP.next);
}
return slowP;
}
2 判斷連結串列中是否有環
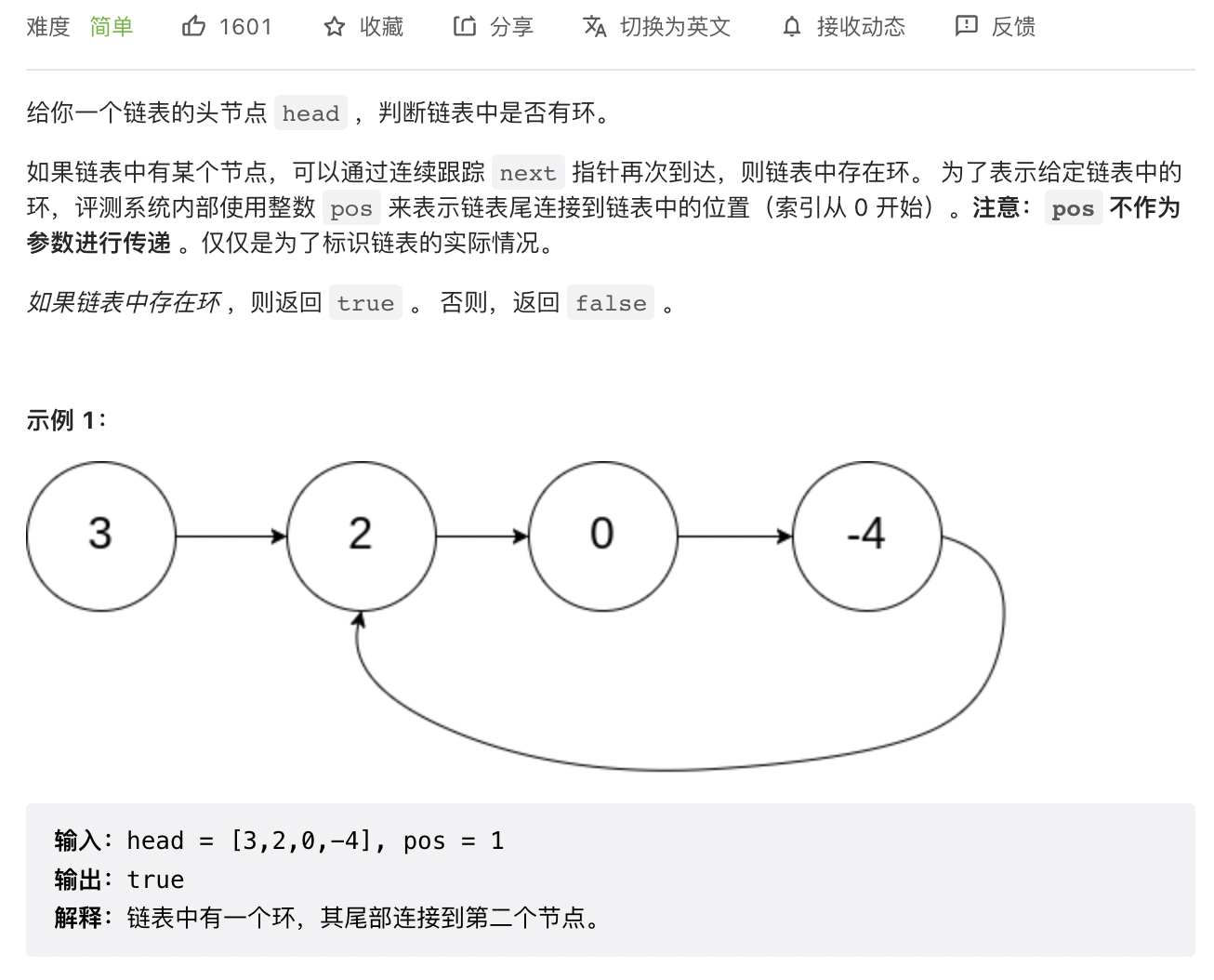
思路
- 設定快慢兩指標 fastP 、slowP
- fastP 每次走 2 步,slowP 每次走 1 步
- 如果連結串列中沒有環,那麼 fastP 最終會先走到 null
- 如果連結串列中有環,那麼 fastP 會先進入環,並在環中轉圈
- 當 slowP 進入環後,fastP 開始追趕 slowP,最終一定能追上
- 當 fastP 追上 slowP 時,若 slowP 走了 n 步,不難得出,fastP 走了 2n 步或 2n - 1 步
程式碼
JS
var hasCycle = function (head) {
// 如果連結串列為空或只有 1 個節點,一定無環
if (!head || !head.next) return false;
let slowP = head;
let fastP = head.next; // slowP 賦值為 head 相當於走了 1 步,故 fastP 要走 2 步
while (fastP) {
slowP = slowP.next;
fastP = fastP.next;
if (slowP === fastP) return true;
fastP && (fastP = fastP.next);
}
return false;
};
// 時間複雜度 O(n) n 為連結串列長度
// 空間複雜度 O(1)
TS
function hasCycle(head: ListNode | null): boolean {
if (!head || !head.next) return false;
let slowP = head;
let fastP = head.next;
while (fastP) {
slowP = slowP.next;
fastP = fastP.next;
if (slowP === fastP) return true;
fastP && (fastP = fastP.next);
}
return false;
}
3 查詢連結串列中環的入口節點
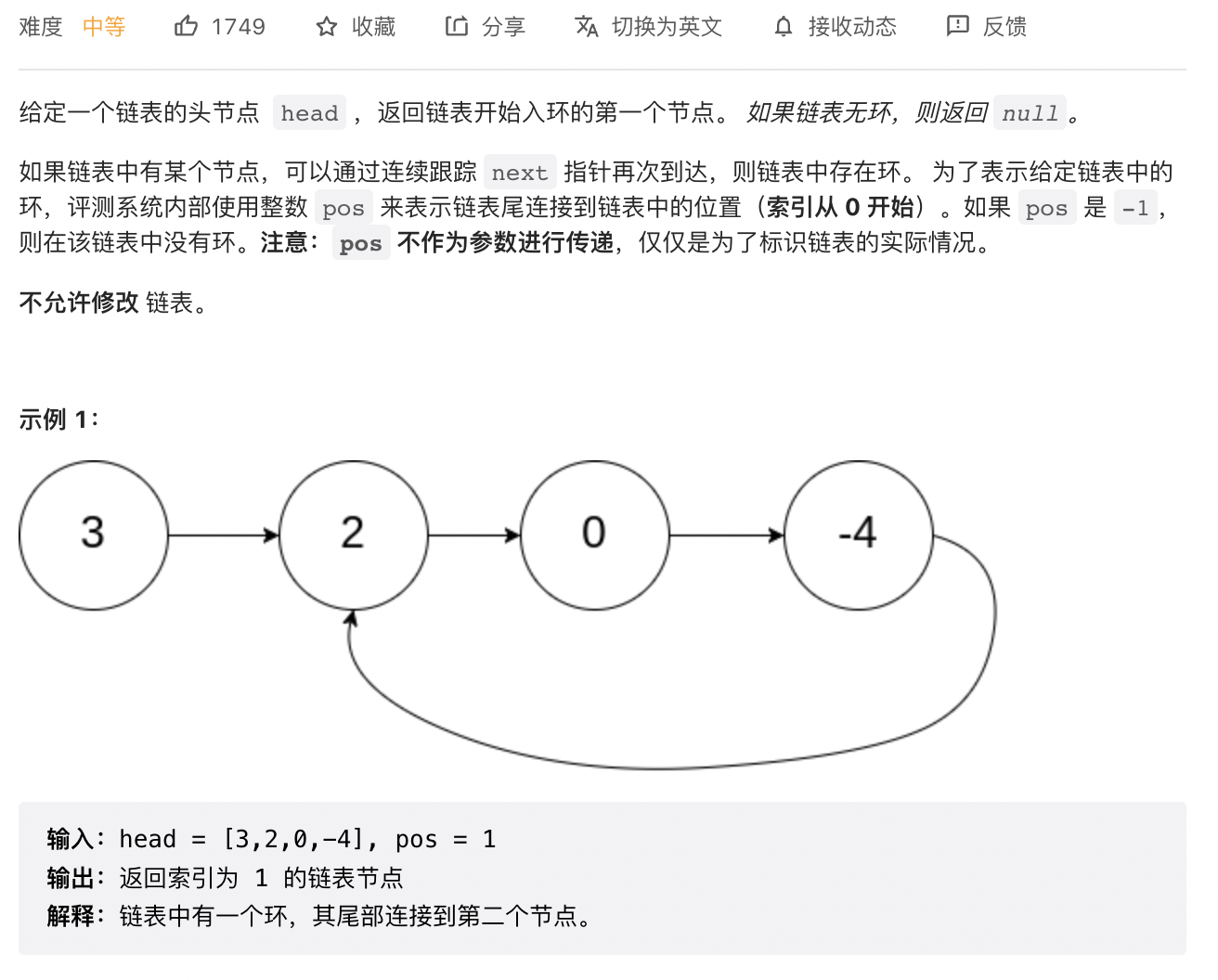
思路
- 此題和上一題的思路大致相同,不過在上一題的基礎上更進一步
- 上一題中提到,如果快指標追上慢指標,且假設 slowP 走了 n 步,不難得出,fastP 走了 2n 步或 2n - 1 步。出現走 2n - 1 步的原因是可能存在 fastP 最後只走 1 步就追上 slowP 的情況
- 不過即使規定 fastP 一定要走偶數步,fastP 和 slowP 也一定能在某點相遇,因為在 fastP 走 2 步,slowP 走 1 步的前提下,兩者的間距會 -1,所以最終兩者會相遇
- 現在設 slowP 走了 n 步,fastP 走了 2n 步,兩者相遇
- 則 fastP 比 slowP 多走了 n 步,這 n 步是環周長的整數倍
- 假設 slowP 從環起點開始走了 k 步後,兩者相遇,則從連結串列頭節點開始走 n - k 步(頭節點算第 1 步)就能到達環起點
- 而從環起點走 k 步到達相遇點,再走 n - k 步就能到達相遇點,因為從環起點走 k + n - k = n 步回到環起點(見第5點,因為 n 是環周長的整數倍)
- 所以我們可以先用快慢指標找到兩者的相遇點,然後讓快指標從頭開始,慢指標從相遇點開始,並且兩者變成同步指標,則兩者再次相遇即為環的起點
程式碼
JS
var detectCycle = function (head) {
if (!head || !head.next) return null;
let fastP = head.next;
let slowP = head;
while (fastP) {
if (fastP === slowP) break;
slowP = slowP.next;
fastP = fastP.next;
fastP && (fastP = fastP.next);
}
if (!fastP) return null;
fastP = head;
slowP = slowP.next; // 注意 fastP 賦值為頭節點相當於已經走了 1 步,所以 slowP 也要走 1 步
while (fastP !== slowP) {
fastP = fastP.next;
slowP = slowP.next;
}
return fastP;
};
// 時間複雜度 O(n)
// 空間複雜度 O(1)
TS
function detectCycle(head: ListNode | null): ListNode | null {
// 這裡我們把頭節點當作虛擬節點
let fastP = head;
let slowP = head;
while (fastP) {
slowP = slowP.next;
fastP = fastP.next;
fastP && (fastP = fastP.next);
if (fastP === slowP) break;
}
if (!fastP) return null;
fastP = head;
slowP = slowP;
while (fastP !== slowP) {
fastP = fastP.next;
slowP = slowP.next;
}
return fastP;
}
注:我們在 TS 中把頭節點當做了虛擬節點,體會兩種解法的細微差別
總結
事實上,使用雙指標的連結串列題還有很多,這裡就舉幾個常見的栗子