小樣本利器3. 半監督最小熵正則 MinEnt & PseudoLabel程式碼實現

在前兩章中我們已經聊過對抗學習FGM，一致性正則Temporal等方案，主要通過約束模型對細微的樣本擾動給出一致性的預測，推動決策邊界更加平滑。這一章我們主要針對低密度分離假設，聊聊如何使用未標註資料來推動決策邊界向低密度區移動，相關程式碼實現詳見ClassicSolution/enhancement

半監督領域有幾個相互關聯的基礎假設

Smoothness平滑度假設：兩個樣本在高密度空間特徵相近，則他們的label大概率相同，宏毅老師美其名曰近朱者赤近墨者黑。這裡的高密度比較難理解，感覺可以近似理解為DBSCAN中的密度可達
Cluster聚類假設：高維特徵空間中，同一個簇的樣本應該有相同的label，這裡的簇其實對應上面平滑假設中的高密度空間。這個假設很強可以理解成Smoothness的特例，在平滑假設中並不一定要成簇
Low-density Separation低密度分離假設：分類邊界應該處於樣本空間的低密度區。這個假設更多是以上假設的必要條件，如果決策邊界處高密度區，則無法保證聚類簇的完整，以及樣本近鄰label一致的平滑假設

我們舉個栗子來理解低密度分離，下圖中藍點和黃點是標註資料樣本，綠點是未標註資料。只使用標註樣本進行訓練，決策邊界可能處於中間空白的任意區域，包括未標註樣本所在的高密度區。如果分類邊界處於高密度區，模型在未標註樣本上的預測熵值會偏高，也就是類別之間區分度較低。因此要推動模型遠離高密度區，可以通過提高模型在無標註樣本上的預測置信度，降低預測熵值來實現，以下給出兩種方案MinEnt和PseudoLabel來實現最小熵正則

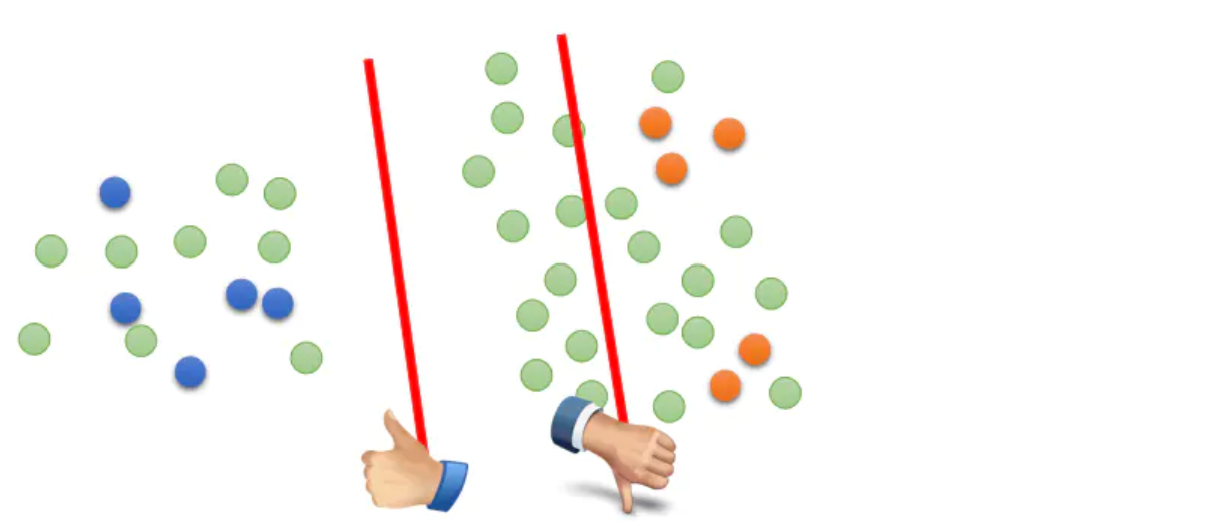
Entropy-Minimization

Paper: Semi-supervised Learning by entropy minimization

在之後很多半監督的論文中都能看到05年這邊Entropy Minimization的相關參照。論文的核心通過最小化未標註樣本的預測概率熵值，來提高模型在以上聚類假設，低密度假設上的穩健性。

實現就是在標註樣本交叉熵的基礎上加入未標註樣本的預測熵值H（y|x），作者稱之為熵正則，並通過\(\lambda\)來控制正則項的權重

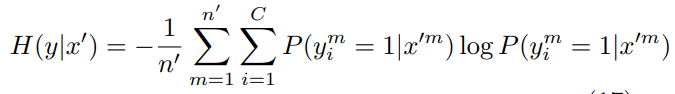
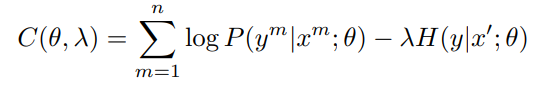
這篇paper咋說呢公式不少，不過都是旁敲側擊的從極大似然等角度來說熵正則有效的原因，但並沒給出嚴謹的證明。。。

Pseudo-Label

paper: Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks

13年提出的Pseudo Label，其實和上面的MinEnt可以說是一個模子出來的。設計很簡單，在訓練過程中直接加入未標註資料，使用模型當前的預測結果，也就是pseudo label直接作為未標註樣本的label，同樣計算交叉熵，並和標註樣本的交叉熵融合得到損失函數，如下

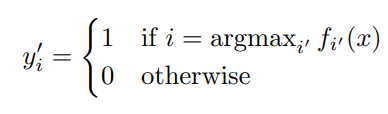
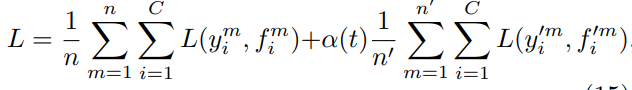
最開始讀會比較疑惑，因為之前瞭解到對pseudo label多是self-training的路子，先用標註資料訓練模型，然後在未標註樣本上預測，篩選高置信的未標註樣本再訓練新模型，訓練多輪直到模型效果不再提升，而這篇文章的實現其實是把未標註樣本作為正則項。因為預測label和預測概率是相同模型給出的，因此最小化預測label的交叉熵，也就是最大化預測為1的class對應的概率值，和MinEnt直接最小化未標註樣本交叉熵的操作可謂殊途同歸~

正則項的權重部分設計的更加精巧一些，作者使用了分段的權重設定，epoch<T1時正則項的權重為0，避免模型最初訓練效果較差時，預測的label準確率低正則項會影響模型收斂，訓練到中段後逐漸提高正則項的權重，超過一定epoch之後，權重停止增長。

以上兩個基於最小熵正則的實現方案都簡單，不過在一些分類任務上嘗試後感覺效果比較玄學，在kaggle上分技巧中有大神說過在一些樣本很小, 整體邊界比較清晰的任務上可能會有提升。主要問題是pseudo label中錯誤的預測值其實就是噪聲樣本，所以會在訓練中引入噪聲，尤其當epoch增長到一定程度後，噪聲樣本對模型擬合的影響會逐漸增加，而最小熵當樣本本身處於錯誤的區域時，預測置信度的提高，其實是增加了錯誤預測的置信度。不過之後一些改良方案中都有借鑑最小熵，所以在後面我們會再提到它~

Reference