MixCSE:困難樣本在句子表示中的使用
Unsupervised Sentence Representation via Contrastive Learning with Mixing Negatives
論文地址:https://www.aaai.org/AAAI22Papers/AAAI-8081.ZhangY.pdf
程式碼地址:https://github.com/BDBC-KG-NLP/MixCSE_AAAI2022
動機:困難樣本挖掘對訓練過程中維持強梯度訊號是至關重要的,同時,隨機取樣負樣本對於句子表示是無效的。
為什麼直接用預訓練的bert得到的句向量不好?
因為各向異性。各向異性是指嵌入在向量空間中佔據一個狹窄的圓錐體。各向異性就有個問題,那就是最後學到的向量都擠在一起,彼此之間計算餘弦相似度都很高,並不是一個很好的表示。一個好的向量表示應該同時滿足Alignment 和 uniformity,前者表示相似的向量距離應該相近,後者就表示向量在空間上應該儘量均勻,最好是各向同性的[1]。因此,才會有一系列的論文旨在解決各向異性,比如bert-flow、bert-whitening。
對比學習在句子表示中的使用?
對比學習就是我們要學習到一個對映,當句子通過這個對映之後,比如x,我們希望和x相似的正樣本的之間的分數要大於和x不相似的負樣本的分數,當然,這個分數我們可以自定義一個計算方式。問題是對於大量的資料而言,我們怎麼去構建正樣本和負樣本? ConsBERT使用大量的資料增強策略,比如token shuffling和cutoff。Kim, Yoo, and Lee利用bert的隱含層表示和最後的句嵌入構建正樣本對。SimCSE 使用不同的dropout mask將相同的句子傳遞給預訓練模型兩次,以構建正樣本對。目前的一些模型主要關注的是在生成正樣本對時使用資料增強策略,而在生成負樣本對時使用隨機取樣策略。在計算機視覺中,困難樣本對於對比學習是至關重要的,而在無監督對比學習中還沒有被探索。
對比學習的基本介紹?
我們先定義一個anchor(錨,可以是任意一個句子) \(h_{i}\),定義\((h_{i}, h_{i}^{'})\)是一個正樣本對,N個負樣本是隨機取樣得到,\((h_{i},h_{j}^{'})\)表示一個負樣本對,那麼我們就有最小化以下的對比損失:
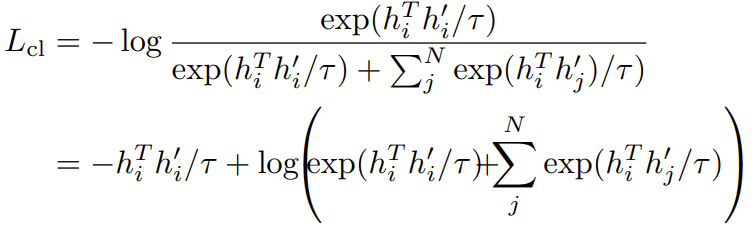
其中\(\tau\)是一個標量溫度超引數。以上損失對\(h_{i}\)求偏導可以得到:
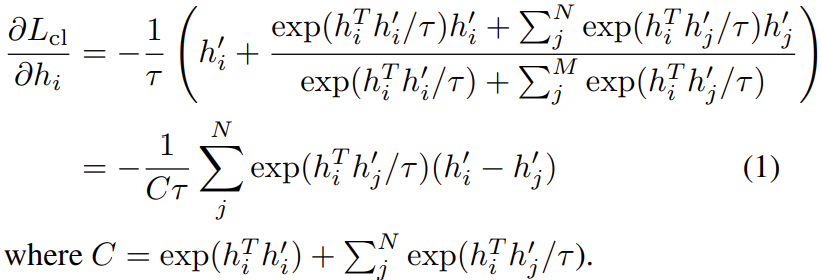
對於每一個負樣本特徵\(h_{j}^{'}\),\(h_{i}\)沿著\(h_{i}^{'}-h_{j}^{'}\)的方向進行更新。由於\(h_{i}^{'}-h_{j}^{'}=(h_{i}^{'}-h_{i})-(h_{j}^{'}-h_{i})\),這可以視為更新是沿著\(h_{i}^{'}-h_{i}\)的方向,而與\(h_{j}^{'}-h_{i}\)方向相反。換句話說,我們會讓正樣本\(h_{i}^{'}\)更接近於\(h_{i}\),而讓負樣本\(h_{j}^{'}\)更遠離\(h_{i}\)。注意到公式(1)中第j項的梯度是依賴於\(exp(h_{i}^{T}h_{j}^{'}/\tau)\),所以它隨內積\(h_{i}^{T}h_{j}^{'}\)呈指數增長。這擴大了和不同負樣本\(h_{j}^{'}\)特徵相關的梯度值。因此,錨點上不易分辨的負特徵\(h_{j}^{'}\)(即那些內積\(h_{i}^{T}h_{j}^{'}\)較大的)接收到更大的梯度訊號,從而將它們推離錨點。
另一方面,注意到\(exp(h_{i}^{T}h_{j}^{'}/\tau)\)<<\(exp(h_{i}^{T}h_{i}^{'}/\tau)\),讓\(exp(h_{i}^{T}h_{j}^{'}/\tau)\)相對於\(exp(h_{i}^{T}h_{i}^{'}/\tau)\)顯得更沒有意義 ,特別是隨著訓練的進行,前者不斷減小,後者不斷增加直至接近\(e\)。然後公式(1)給出的梯度訊號不斷減小,使得訓練變慢甚至停止。
在這一點上,我們看到錨附近的負特徵的存在對於保持強梯度訊號是至關重要的。我們將這種難以區分的負面特徵稱為「困難負面特徵」。這項工作的關鍵發展是不斷地在訓練過程中注入人工的困難負面特徵,因為原本的困難負面特徵正在被推開,變得「更容易」。
MixCSE的基本介紹?
該方法在訓練過程中不斷地注入人工困難負特徵,從而在整個訓練過程中保持強梯度訊號。
對於錨特徵\(h_{i}\),通過混合正特徵\(h_{i}^{'}\)和隨機負特徵\(h_{j}^{'}\)構建負特徵:
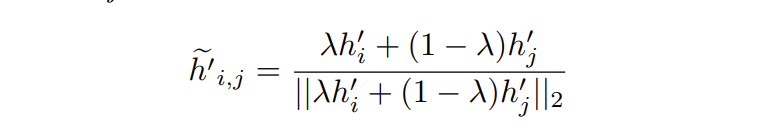
\(\lambda\)是一個超引數,用於控制混合的程度。包含這些混合負特徵後,對比損失變為:
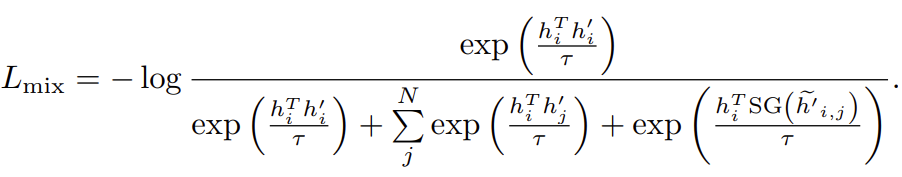
\(SG(.)\)定義為梯度停止,確保在反向傳播時不會經過混合負樣本。
接著,我們注意到錨和混合負樣本的內積:
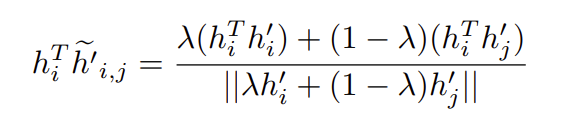
在某些階段,\(h_{i}^{T}\widetilde{h}_{i,j}^{'}\approx0\)。另外,在實現對齊時,\(h_{i}^{T}h_{i}^{'}\approx1\)。則有:
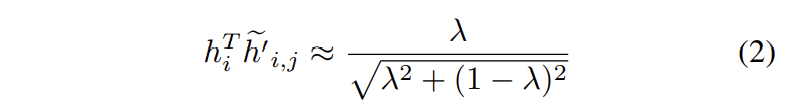
不像標準的負特徵\(h_{j}^{i}\)有\(h_{i}^{T}h_{j}^{'}\approx0\)的風險。混合負特徵確保內積值始終高於零。這樣的負特徵則有助於保持更強的梯度訊號。
怎麼選擇\(\lambda\)?
假設有兩個正樣本特徵\(h_{i}^{'}\)和\(h_{i}^{''}\),角度分別為\(0\)和\(\gamma\)。
錨和混合負樣本間的角度計算為:
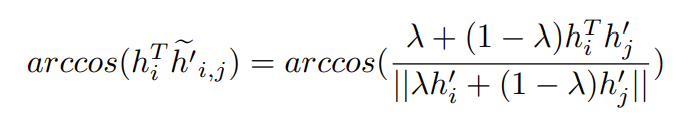
我們既要讓混合負樣本更接近錨,同時也要讓正樣本和錨之間比正樣本和混合負樣本之間更接近,因此\(\lambda\)有一個上界:
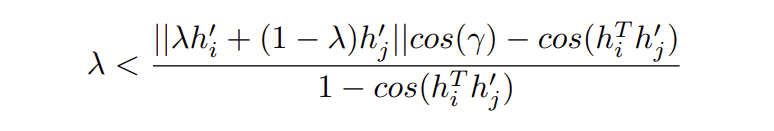
但是我們並不知道\(\gamma\)的值,因此設定較小的\(\lambda\)以避免獲得錯誤的困難樣本。
為什麼不讓混合負樣本參與反向傳播?
如果參與,計算梯度如下:

我們看到會有一項:
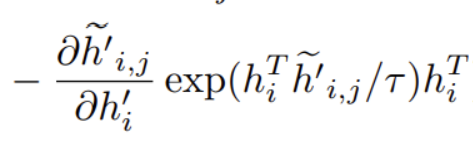
它會使得正樣本\(h_{i}^{i}\)逐漸遠離\(h_{i}\)。
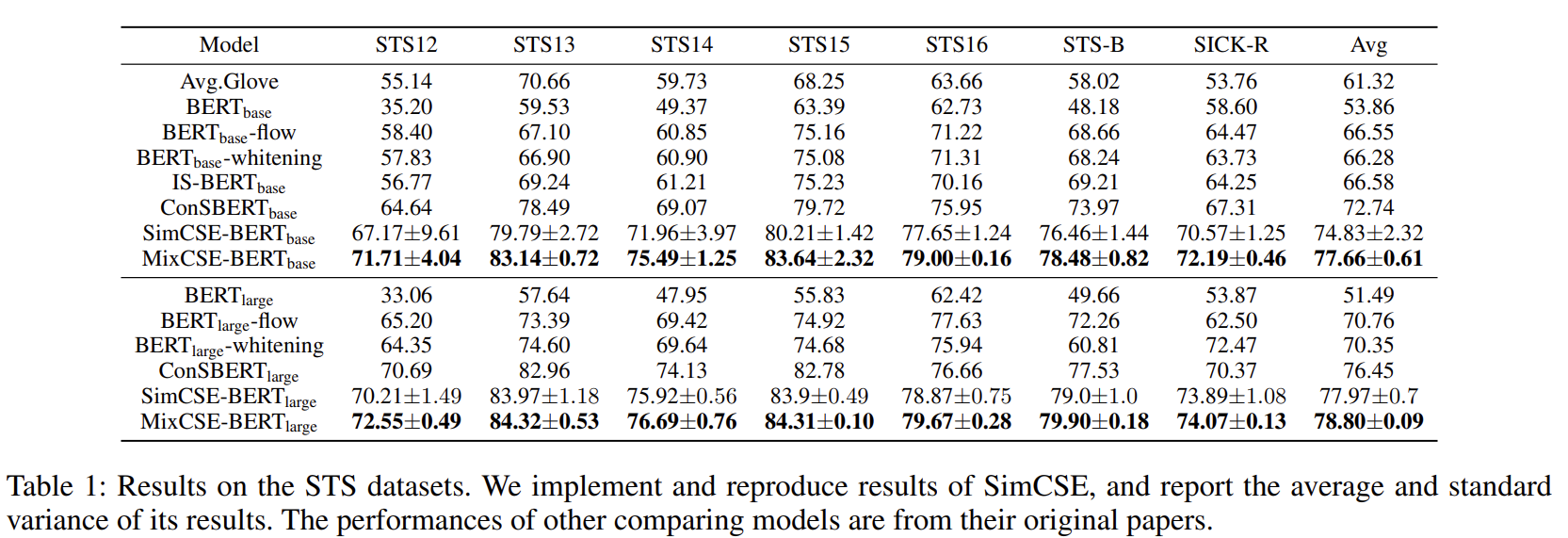
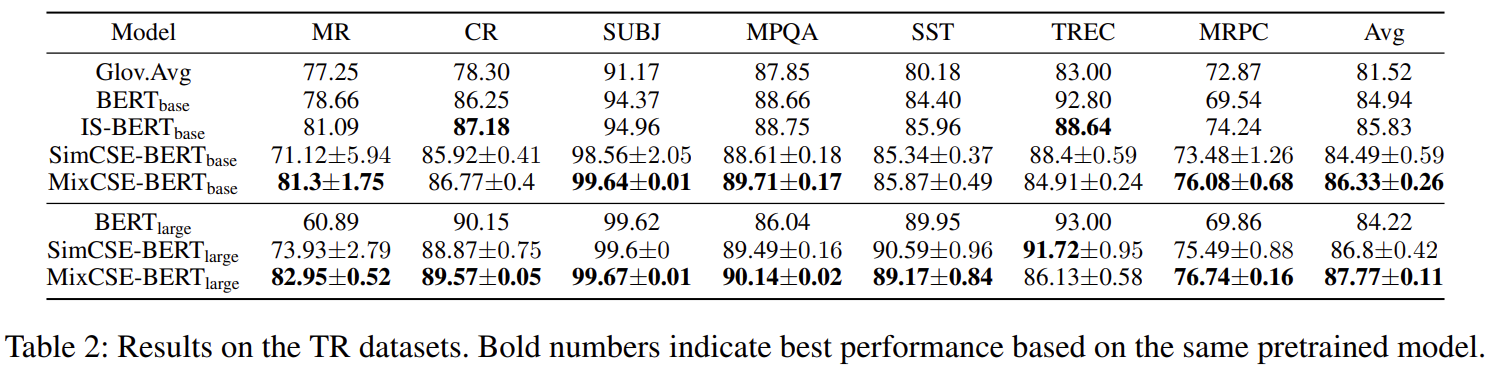
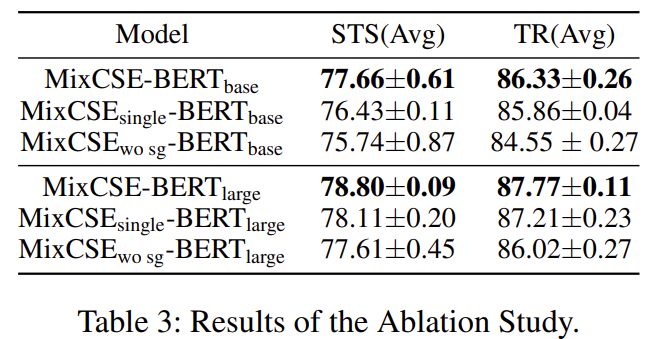
實驗結果?