「學習筆記」字串基礎：Hash，KMP與Trie

點選檢視目錄

目錄
「學習筆記」字串基礎：Hash，KMP與Trie
Hash
演演算法
程式碼
KMP
演演算法
前置知識：$\text{Border}$
思路
程式碼
$\text{KMP}$ 匹配
思路
程式碼
Trie
資料結構
01-Trie
程式碼
練習題
Hash
Bovine Genomics
思路
程式碼
[TJOI2018]鹼基序列
思路
程式碼
[CQOI2014]萬用字元匹配
[NOI2017] 蚯蚓排隊
思路
程式碼
KMP
Seek the Name, Seek the Fame
思路
程式碼
[NOI2014] 動物園
思路
程式碼
[USACO15FEB] Censoring S
思路
程式碼
[POI2006] OKR-Periods of Words
思路
程式碼
字串的匹配
思路
程式碼
[HNOI2008]GT考試
思路
程式碼
Trie
Phone List
思路
程式碼
The XOR Largest Pair
思路
程式碼
The XOR-longest Path
思路
程式碼
Nikitosh 和互斥或
思路
程式碼

Hash

演演算法

為了方便處理字串，我們可以把一個字串轉化成如下形式（$s$ 為原字串，$l$ 為字串長度，$b$ 為進位制，$P$ 為防止溢位的大質數）：

\[\operatorname{Hash}(s)=\sum_{i=1}^{l}s_i*b^{l-i}\bmod{P} \]

其中，$b$ 一般選取一個三位質數即可（建議用 $233$），而 $P$ 一般要選一個大質數。

我們可以直接通過比較兩個字串的雜湊值是否相等來比較它們是否一樣，但是顯然兩個不一樣字串的雜湊值也是有很小的概率相等的，這種 $\operatorname{Hash}$ 函數值一樣時原字串卻不一樣的現象我們稱為雜湊碰撞。

我們可以通過雙模數來降低雜湊碰撞的概率，但是要注意儘量不要選取常用的質數（如 $10^9+7,10^9+9,998244353$），否則出題人會故意卡你。

我的建議是背幾個不常用的質數（如 $315716251,475262633$），或者考場上現造質數。

咋現造啊

Linux 終端有個指令叫 factor，分解質因數用的。

亂寫一堆數然後分解一下選幾個比較大的不越界的質數（一般用九位數就行，如果是雜湊表這樣用來開陣列的選個八位數）即可。

嗯上邊那倆質數就是這樣幹出來的。

處理一整個字串的字首的時間複雜度是 $\Theta(\left|S\right|)$，直接用 $\left(\operatorname{Hash}(i-1)+s_i*b^{i-1}\right)$ 得到 $\operatorname{Hash}(i)$即可。

如何快速求 $S_l\sim S_r$ 的雜湊值？直接用 $\left(\operatorname{Hash}(r)-\operatorname{Hash}(l-1)\times b^{r-l+1}\right)$ 就可以算出，時間複雜度是 $\Theta(1)$。

程式碼

點選檢視程式碼

class Hash{
public:
	const ll P1=315716251,P2=475262633;
	ll h1[N],h2[N],z1[N],z2[N];
	inline void Init(char *s,ll k){
		ll len=strlen(s+1);
		ll b=233;
		z1[0]=z2[0]=1;
		_for(i,1,len){
			z1[i]=z1[i-1]*b%P1;
			z2[i]=z2[i-1]*b%P2;
			h1[i]=(h1[i-1]*b+(s[i]-'A'+1)%P1)%P1;
			h2[i]=(h2[i-1]*b+(s[i]-'A'+1)%P2)%P2;
		}
		return;
	}
	inline ll GetHash1(ll l,ll r){return (h1[r]-h1[l-1]*z1[r-l+1]%P1+P1)%P1;}
	inline ll GetHash2(ll l,ll r){return (h2[r]-h2[l-1]*z2[r-l+1]%P2+P2)%P2;}
}a,b;

KMP

演演算法

（這裡的程式碼都是直接從模板題粘過來的）

前置知識：$\text{Border}$

思路

先來幾個定義：

$Pre_i$ 一個字串長為 $i$ 的字首。
一個字串 $s$ 的 $\text{Border}$ 為一個同時是 $s$ 前字尾的真子串。
例如 abab 和 ab 就是 ababab 的 $\text{Border}$，而 aba 和 a 則不是。
$nxt_i$ 表示當前字串長為 $i$ 的字首最長的 $\text{Border}$ 的長度。

$nxt_i$ 陣列的應用十分廣泛，$\text{KMP}$ 只是其中的應用之一。

這個陣列可以 $\Theta(n^2)$ 求，但效率太低了，那麼如何 $\Theta(n)$ 求這個東西呢？

首先給出一個字串 $s$，我們假設之前的 $nxt_{1}\sim nxt_{11}$ 都已經求完了，現在要求 $nxt_{12}$（最後的那個）。

abcabdabcabc
00012012345?

$nxt_{11}=5$，可以看出這個 $\text{Border}$ 是 abcab：

abcab d abcab | c
[---]
		[---] |

我們嘗試把它往後推一位，但是 $s_6\neq s_{12}$，也就是說失配了！

這個時候我們看一眼 $nxt_{nxt_{11}}$，即 $nxt_5=2$，$\text{Border}$ 是 ab：

abcab | dabcabc
[]	  | 
   [] |

由於 $s_1\sim s_5=s_7\sim s_{11}$，我們可以把 $s_1\sim s_5$ 的 $\text{Border}$ 推廣到 $s_7\sim s_{11}$上，即 $s_7\sim s_8=s_{10}\sim s_{11}$：

abcabdabcabc
[]-[]
	  []-[]

$s_1\sim s_5=s_7\sim s_{11}$，所以 $s_1\sim s_2=s_{7}\sim s_{8}$ 且 $s_4\sim s_5=s_{10}\sim s_{11}$，即 $s_1\sim s_2=s_{10}\sim s_{11}$：

abcabdabcabc
[]
		 []

這個時候我們再繼續往後推，可以發現 $s_3\neq s_{12}$，能夠匹配上了！

那麼最後算出 $nxt_{12}=3$。

abcabdabcabc
[-]
		 [-]

最後總結一下求 $nxt_{i}$ 的步驟：

令 $j=nxt_{i-1}$。
嘗試匹配 $s_{j+1}$ 和 $s_i$ 如果失配則令 $j=nxt_{j}$ 並不斷迴圈此步，直到 $j=0$ 或匹配成功。
令 $nxt_i=j+[s_{j+1}=s_i]$。

程式碼

inline void PreNxt(){
	nxt[1]=0;ll k=0;
	_for(i,2,m){
		while(k&&t[i]!=t[k+1])k=nxt[k];
		k+=(t[i]==t[k+1]),nxt[i]=k;
	}
	return;
}

$\text{KMP}$ 匹配

$\text{Hot Knowlegde}$

該演演算法由 Knuth、Pratt 和 Morris 在 1977 年共同釋出 ^[1]。

思路

定義：

模式串是要查詢的串。
文字串是被查詢的串。

$\text{KMP}$ 演演算法的思路其實和求 $nxt$ 陣列差不多，如果當前兩個串失配了，那麼我們在模式串中不斷跳 $nxt_{nxt_{nxt_{\cdots}}}$，直到匹配成功再繼續往下。

（個人認為 $nxt$ 陣列更像一個指標，它指向位置的是失配後重新匹配的最優位置）

程式碼

下面這份程式碼中，文字串是 $s$，模式串是 $t$，在執行前需要已經求出 $nxt$ 陣列，輸出的是模式串在文字串中每次出現的起始位置。

inline void Matching(){
	ll k=0;
	_for(i,1,n){
		while(k&&s[i]!=t[k+1])k=nxt[k];
		k+=(s[i]==t[k+1]);
		if(k==m){
			printf("%lld\n",i-m+1);
			k=nxt[k];
		}
	}
}

Trie

TRIE=sTRIng+TReE

資料結構

Trie 就是把一堆字串放到樹上方便查詢。

例如我們插入以下幾個單詞

apple
cat
copy
coffee

就會長出這樣一棵 Trie：

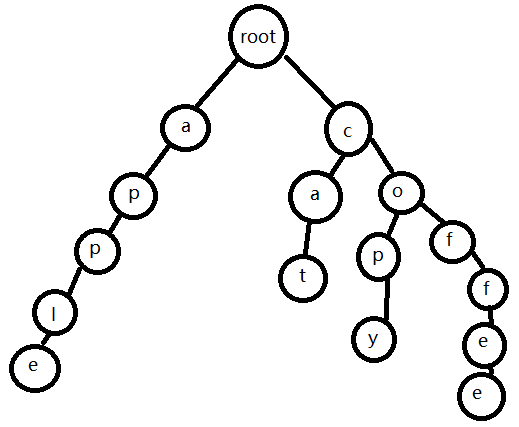
~~好像有點醜~~ 確實有點醜。

01-Trie

指字元集為 $\{0,1\}$ 的 Trie。

把數位換成二進位制後塞到 Trie 裡就得到了 01-Trie。

01-Trie 有很多應用，例如維護互斥或極值。

程式碼

class Trie{
private:
	ll tot=1;
	class{public:ll nx[26];bool end;}tr[N];
public:
	inline void Add(char *s){
		ll len=strlen(s+1),p=1;
		_for(i,1,len){
			if(!tr[p].nx[s[i]-'a'])tr[p].nx[s[i]-'a']=++tot;
			p=tr[p].nx[s[i]-'a'];
		}
		tr[p].end=1;
		return;
	}
	inline bool Find(char *s){
		ll len=strlen(s+1),p=1;
		_for(i,1,len){
			if(!tr[p].nx[s[i]-'a'])return 0;
			p=tr[p].nx[s[i]-'a'];
		}
		return tr[p].end;
	}
}tr;

練習題

Hash

Bovine Genomics

思路

可以列舉左右端點暴力比較，確定好左右端點和要比較的兩個字串之後可以 $\Theta(1)$ 雜湊比較，但顯然總複雜度 $\Theta(n^4)$ 跑不動，考慮如何優化。

這道題讓我們求最短區間長度，那麼我們考慮二分答案這個長度。

但這樣複雜度是 $\Theta(n^3\log_2n)$ 的，依舊跑不動。

可以發現我沒有必要將所有字串都匹配一遍，只需要判斷當前這個區間有沒有重複出現，那麼我們直接把雜湊值丟進一個 map 裡面維護即可，複雜度 $\Theta(n^2\log_2^2n)$。

但是不能直接把字串丟進 map 裡，因為這種情況 map 不是現雜湊就是用 Trie，單次更改/查詢複雜度都是 $\Theta(n)$。

程式碼

點選檢視程式碼

const ll N=510,inf=1ll<<40;
ll n,m,ans,le,ri;
char s[N][N],t[N][N];
map<ll,bool>mp1,mp2;
class Hash{
public:
	const ll P1=315716251,P2=475262633;
	ll h1[N],h2[N],z1[N],z2[N];
	inline void Init(char *s){
		ll len=strlen(s+1);
		z1[0]=z2[0]=1;
		_for(i,1,m){
			z1[i]=z1[i-1]*233%P1;
			z2[i]=z2[i-1]*233%P2;
			h1[i]=(h1[i-1]*233+(s[i]-'A'+1)%P1)%P1;
			h2[i]=(h2[i-1]*233+(s[i]-'A'+1)%P2)%P2;
		}
		return;
	}
	inline ll GetHash1(ll l,ll r){return (h1[r]-h1[l-1]*z1[r-l+1]%P1+P1)%P1;}
	inline ll GetHash2(ll l,ll r){return (h2[r]-h2[l-1]*z2[r-l+1]%P2+P2)%P2;}
}a[N],b[N];
namespace SOLVE{
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	inline bool Check(ll len){
		_for(i,len,m){
			bool bl=1;
			mp1.clear(),mp2.clear();
			_for(j,1,n){
				mp1[a[j].GetHash1(i-len+1,i)]=1;
				mp2[a[j].GetHash2(i-len+1,i)]=1;
			}
			_for(j,1,n){
				if(mp1[b[j].GetHash1(i-len+1,i)])bl=0;
				if(mp2[b[j].GetHash2(i-len+1,i)])bl=0;
			}
			if(bl)return 1;
		}
		return 0;
	}
	inline void In(){
		n=rnt(),m=rnt();
		_for(i,1,n)scanf("%s",s[i]+1),a[i].Init(s[i]);
		_for(i,1,n)scanf("%s",t[i]+1),b[i].Init(t[i]);
		ll l=1,r=m;
		while(l<r){
			bdmd;
			if(Check(mid))r=mid;
			else l=mid+1;
		}
		printf("%lld\n",l);
		return;
	}
}

[TJOI2018]鹼基序列

思路

設 $t_{i,j}$ 是 $i$ 個氨基酸的第 $j$ 種，$f_{i,j}$ 表示第 $i$ 個氨基酸的結尾放在 $j$ 的方案數，則轉移方程為：

\[f_{i,j}=\sum_{i=\left|t_{i,j}\right|}^{\left|S\right|}[S_{i-\left|t_{i,j}\right|+1}\sim S_i=\!=t_{i,j}] \]

陣列可以滾一下，但感覺沒什麼必要。

比較直接雜湊，時間複雜度 $\Theta(ka_i\left|S\right|)$。

程式碼

點選檢視程式碼

const ll N=1e4+10,P=1e9+7,inf=1ll<<40;
ll n,a[N],l,f[110][N],ans;
char s[N],t[N];
vector<ll>pp;
class Hash{
public:
	const ll P1=315716521,P2=475262633;
	ll h1[N],h2[N],z1[N],z2[N];
	inline void Init(char *s){
		z1[0]=z2[0]=1;
		ll length=strlen(s+1);
		_for(i,1,length){
			z1[i]=z1[i-1]*233%P1;
			z2[i]=z2[i-1]*233%P2;
			h1[i]=(h1[i-1]*233+(s[i]-'A'+1)%P1)%P1;
			h2[i]=(h2[i-1]*233+(s[i]-'A'+1)%P2)%P2;
		}
		return;
	}
	inline ll GetHash1(ll l,ll r){return (h1[r]-h1[l-1]*z1[r-l+1]%P1+P1)%P1;}
	inline ll GetHash2(ll l,ll r){return (h2[r]-h2[l-1]*z2[r-l+1]%P2+P2)%P2;}
}d;
namespace SOLVE{
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	inline ll GetS1(char *s){
		ll s1=0;
		_for(i,1,strlen(s+1))s1=(s1*233+s[i]-'A'+1)%d.P1;
		return s1;
	}
	inline ll GetS2(char *s){
		ll s2=0;
		_for(i,1,strlen(s+1))s2=(s2*233+s[i]-'A'+1)%d.P2;
		return s2;
	}
	inline void In(){
		n=rnt();
		scanf("%s",s+1);
		l=strlen(s+1);d.Init(s);
		_for(i,1,n){
			ll a=rnt();
			_for(j,1,a){
				scanf("%s",t+1);
				ll len=strlen(t+1);
				ll s1=GetS1(t),s2=GetS2(t);
				_for(k,len,l){
					if(d.GetHash1(k-len+1,k)!=s1)continue;
					if(d.GetHash2(k-len+1,k)!=s2)continue;
					f[i][k]=(f[i][k]+f[i-1][k-len])%P;
					if(i==1&&!f[i-1][k-len])++f[i][k];
				}
			}
		}
		_for(i,1,l)ans=(ans+f[n][i])%P;
		printf("%lld\n",ans);
		return;
	}
}

[CQOI2014]萬用字元匹配

題解在這裡

[NOI2017] 蚯蚓排隊

思路

觀察資料範圍可以發現 $k\le50$。

那麼就可以暴力去跑了，簡單來說：

對於操作一：把在拼接處新拼接出的所有向後 $k$ 字串（$1\le k\le50$）記錄。
對於操作二：把在斷開處層拼接出的所有向後 $k$ 字串（$1\le k\le50$）去除。
對於操作三：暴力列舉 $S$ 的每個長度為 $k$ 的子串，累計出現次數。

那麼如何記錄呢？再看題面還可以發現我們不用去逐位比較，只要記錄每個串出現次數即可。

我剛開始用的是 map，但自帶一個 $\log$ 會超時。

那麼我們引入一個東西叫 雜湊表，簡單來說就是先對原串雜湊值取個模得到 $x$，然後開個連結串列存取模後得到 $x$ 的所有雜湊值。查詢時直接把存取模後得到 $x$ 的所有雜湊值的連結串列全部遍歷一遍來查詢。因為雜湊衝突概率本來就很小，所以用不了查詢多久。

時間複雜度 $\Theta(km+\sum\left|S\right|)$。

程式碼

點選檢視程式碼

const ll N=1e7+10,MOD=998244353,P=19491001,inf=1ll<<40;
ll n,m,ans,arry[110],ss[N];ull z[110],h[110];char t[N];
class lb{public:ll la,nx,va;}lb[N];
namespace Hash{
	class HashTable{
	public:
		ll tot=0,hd[P]={0};
		class Table{
		public:
			ull hv;ll cnt,nx;
			inline void Add(ull a,ll b,ll c){hv=a,cnt=b,nx=c;}
		}t[P*2];
		inline void Add(ull val){
			ll v=val%P;ll f=hd[v];
			while(f&&t[f].hv!=val)f=t[f].nx;
			if(!f)t[++tot].Add(val,1,hd[v]),hd[v]=tot;
			else ++t[f].cnt;
			return;
		}
		inline void Del(ull val){
			ll v=val%P;ll f=hd[v];
			while(f&&t[f].hv!=val)f=t[f].nx;
			if(f)--t[f].cnt;
			return;
		}
		inline ll Que(ull val){
			ll v=val%P;ll f=hd[v];
			while(f&&t[f].hv!=val)f=t[f].nx;
			if(f)return t[f].cnt;
			return 0;
		}
	}ha;
	inline void Merge(ll a,ll b){
		ll st=a,en=a,le=1,ri=0;
		lb[a].nx=b,lb[b].la=a;
		while(lb[st].la!=-1&&le<50)st=lb[st].la,++le;
		_for(i,1,le)h[i]=h[i-1]*131+lb[st].va,st=lb[st].nx;
		while(lb[en].nx!=-1&&ri<=50)en=lb[en].nx,++ri,h[le+ri]=h[le+ri-1]*131+lb[en].va;
		_for(i,1,le)_for(j,le+1,min(ri+le,i+49))ha.Add(h[j]-h[i-1]*z[j-i+1]);
		return;
	}
	inline void Divition(ll k){
		ll st=k,en=k,le=1,ri=0;
		while(lb[st].la!=-1&&le<50)st=lb[st].la,++le;
		_for(i,1,le)h[i]=h[i-1]*131+lb[st].va,st=lb[st].nx;
		while(lb[en].nx!=-1&&ri<=50)en=lb[en].nx,++ri,h[le+ri]=h[le+ri-1]*131+lb[en].va;
		_for(i,1,le)_for(j,le+1,min(ri+le,i+49))ha.Del(h[j]-h[i-1]*z[j-i+1]);
		lb[lb[k].nx].la=-1,lb[k].nx=-1;
		return;
	}
	inline ll Query(ll k,ll len){
		ll ans=1;ull val=0;
		_for(i,1,len){
			if(i>k)val-=z[k-1]*ss[i-k];
			val=val*131+ss[i];
			if(i>=k)ans=ans*ha.Que(val)%MOD;
		}
		return ans;
	}
}
using namespace Hash;
namespace SOLVE{
	char buf[1<<20],*p1,*p2;
	#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	inline ll rnt(){
		ll x=0,w=1;char c=gc();
		while(!isdigit(c)){if(c=='-')w=-1;c=gc();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=gc();
		return x*w;
	}
	inline void In(){
		n=rnt(),m=rnt(),z[0]=1;
		_for(i,1,100)z[i]=z[i-1]*131;
		_for(i,1,n){
			lb[i].va=rnt()+'0';
			lb[i].nx=lb[i].la=-1;
			Hash::ha.Add(lb[i].va);
		}
		_for(i,1,m){
			ll op=rnt();
			if(op==1){
				ll x=rnt(),y=rnt();
				Merge(x,y);
			}
			else if(op==2){
				ll x=rnt();
				Divition(x);
			}
			else{
				char c=gc();ll t=0;
				while(!isdigit(c))c=gc();
				while(isdigit(c))ss[++t]=c,c=gc();
				ll k=rnt();
				printf("%lld\n",Query(k,t));
			}
		}
		return;
	}
}

KMP

Seek the Name, Seek the Fame

思路

板子題，因為 $\text{Border}$ 的 $\text{Border}$ 還是 $\text{Border}$，所以一路 $nxt$ 下去就可以了。

程式碼

點選檢視程式碼

inline void PreNxt(){
	nxt[0]=0;ll j=0;
	_for(i,2,n){
		while(j&&s[i]!=s[j+1])j=nxt[j];
		if(s[i]==s[j+1])++j;
		nxt[i]=j;
	}
	return;
}
void Print(ll i){
	if(i<1)return;
	Print(nxt[i]-(bool)(nxt[i]==i));
	printf("%lld ",i);
	return;
}
inline void In(){
	n=strlen(s+1);
	PreNxt(),Print(n),puts("");
	return;
}

[NOI2014] 動物園

思路

題目要求不重疊的 $\text{Border}$ 數量，那麼我們可以先求出一個 $cnt$ 陣列表示 可重疊的 $\text{Border}$ 數量。

不難發現我們找到一個長度不超過 $\tfrac{k}{2}$ 的最長的 $\text{Border}$：$Pre_k$，則 $num_i=cnt_k$。

而 $cnt$ 的求法也很簡單：$cnt_i=cnt_{nxt_i}+1$，求 $nxt$ 時順便求一下就行了。

程式碼

程式碼裡的 num 就是 cnt。

點選檢視程式碼

inline void PreNxt(){
	nxt[1]=0,num[1]=1;ll j=0;
	_for(i,2,n){
		while(j&&s[i]!=s[j+1])j=nxt[j];
		if(s[i]==s[j+1])++j;
		nxt[i]=j,num[i]=num[j]+1;
	}
	return;
}
inline void SolveNum(){
	ans=1;ll k=0;
	_for(i,2,n){
		while(k&&s[i]!=s[k+1])k=nxt[k];
		if(s[i]==s[k+1])++k;
		while(k&&(k<<1)>i)k=nxt[k];
		ans=ans*(num[k]+1)%P;
	}
	return;
}
inline void In(){
	scanf("%s",s+1);
	n=strlen(s+1);
	PreNxt(),SolveNum();
	printf("%lld\n",ans);
	return;
}

[USACO15FEB] Censoring S

思路

本題的難點在於如何刪除一個子串。

考慮用一個棧 st 維護當前剩下的串，每次匹配成功後把這個匹配成功的子串彈出去，再讓下一個字元從棧頂繼續匹配（即 j=nxt[st[top]]）。因為之前已經將中間的匹配成功的串彈了出去，所以該演演算法正確。

程式碼

點選檢視程式碼

const ll N=2e6+10,inf=1ll<<40;
ll n,m,nxt[N],f[N],st[N],top,ans;char s[N],t[N];
namespace SOLVE{
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	inline ll rnt(){
		ll x=0,w=1;char c=gc();
		while(!isdigit(c)){if(c=='-')w=-1;c=gc();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=gc();
		return x*w;
	}
	inline void PreNxt(){
		ll j=0;
		_for(i,2,m){
			while(j&&t[j+1]!=t[i])j=nxt[j];
			if(t[j+1]==t[i])++j;
			nxt[i]=j;
		}
		return;
	}
	inline void Machting(){
		ll j=0;
		_for(i,1,n){
			st[++top]=i;
			while(j&&t[j+1]!=s[i])j=nxt[j];
			if(t[j+1]==s[i])++j;
			f[i]=j;
			if(j==m){
				top-=m;
				j=f[st[top]];
			}
		}
		return;
	}
	inline void Print(){
		_for(i,1,top)putchar(s[st[i]]);
		return;
	}
	inline void In(){
		scanf("%s%s",s+1,t+1);
		n=strlen(s+1),m=strlen(t+1);
		PreNxt(),Machting();
		Print(),puts("");
		return;
	}
}

[POI2006] OKR-Periods of Words

思路

設一個字串 $s$ 長度為 $L$，最長週期長度為 $l$，可以發現 $s_{l+1}\sim s_{L}$ 是第二遍迴圈的 $Q$ 的字首，也就是說 $s_{l+1}\sim s_{L}$ 是 $S$ 的一個 $\text{Border}$！

可以發現這個 $\text{Border}$ 的長度越小 $l$ 越大，那麼我們就把問題轉化成了 求一個字串所有字首的最小 $\text{Border}$ 長度之和。

設 $mn_i$ 表示 $Pre_i$ 的最小 $\text{Border}$ 長度，分情況討論它的值：

如果 $Pre_i$ 只有一個 $\text{Border}$，那麼 $mn_i=nxt_i$。
否則由於 $\text{Border}$ 的 $\text{Border}$ 是 $\text{Border}$，直接令 $mn_i=mn_{nxt_i}$。

程式碼

注意：如果輸入時要數位和字串混輸就不要用 fread，否則會把字串讀到緩衝區裡，導致無法讀入字串。（也可以單獨再寫一個讀入字串的函數，但是太麻煩沒必要）

點選檢視程式碼

const ll N=1e6+10,inf=1ll<<40;
ll n,nxt[N],mn[N],ans;char s[N];
namespace SOLVE{
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	inline void PreNxt(){
		ll j=0;
		_for(i,2,n){
			while(j&&s[i]!=s[j+1])j=nxt[j];
			if(s[i]==s[j+1])++j;
			nxt[i]=j;
			if(j&&!nxt[j])mn[i]=j;
			else mn[i]=mn[j];
			if(mn[i])ans+=i-mn[i];
		}
	}
	inline void In(){
		n=rnt();
		scanf("%s",s+1);
		PreNxt();
		printf("%lld\n",ans);
		return;
	}
}

字串的匹配

思路

顯然無法直接比較，因為需要求出在區間中的排名。

考慮用樹狀陣列維護排名，但是直接維護任意區間的排名是很困難的。

再次像之前一樣研究 $\text{Border}$ 的性質。在求 $nxt$ 陣列時可以發現 每次失配時 $\text{Border}$ 左端點都會減小，匹配成功後右端點加一，即這個區間是個整體不斷右移的區間，且完全不會左移。

那麼每次失配就可以把左邊的數暴力去除貢獻，總複雜度 $\Theta(n)$。

會算排名後就可以直接匹配了。

時間複雜度 $\Theta(n\log_2n)$。

程式碼

點選檢視程式碼

const ll N=5e5+10,inf=1ll<<40;
ll n,m,s,rk1[N],rk2[N],nxt[N],a[N],b[N];vector<ll>ans;
class BIT{
public:
	ll b[N]={0};
	inline void Update(ll x,ll y){while(x>0&&x<=s)b[x]+=y,x+=(x&-x);return;}
	inline ll Query(ll x){ll sum=0;while(x>0)sum+=b[x],x-=(x&-x);return sum;}
	inline void Clear(){memset(b,0,sizeof(b));}
}r,bit;
namespace SOLVE{
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	inline ll rnt(){
		ll x=0,w=1;char c=gc();
		while(!isdigit(c)){if(c=='-')w=-1;c=gc();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=gc();
		return x*w;
	}
	inline bool Check(ll a,ll b){
		return bit.Query(a-1)==rk1[b]&&bit.Query(a)==rk2[b];
	}
	inline void PreRank(){
		_for(i,1,m){
			r.Update(b[i],1);
			rk1[i]=r.Query(b[i]-1);
			rk2[i]=r.Query(b[i]);
		}
		return;
	}
	inline void PreNxt(){
		nxt[1]=0;
		ll j=0;
		_for(i,2,m){
			bit.Update(b[i],1);
			while(j&&!Check(b[i],j+1)){
				_for(k,i-j,i-nxt[j]-1)bit.Update(b[k],-1);
				j=nxt[j];
			}
			if(Check(b[i],j+1))++j;
			nxt[i]=j;
		}
		return;
	}
	inline void Matching(){
		bit.Clear();
		ll j=0;
		_for(i,1,n){
			bit.Update(a[i],1);
			while(j&&!Check(a[i],j+1)){
				_for(k,i-j,i-nxt[j]-1)bit.Update(a[k],-1);
				j=nxt[j];
			}
			if(Check(a[i],j+1))++j;
			if(j==m){
				ans.push_back(i-j+1);
				_for(k,i-j+1,i-nxt[j])bit.Update(a[k],-1);
				j=nxt[j];
			}
		}
		return;
	}
	inline void In(){
		n=rnt(),m=rnt(),s=rnt();
		_for(i,1,n)a[i]=rnt();
		_for(i,1,m)b[i]=rnt();
		PreRank(),PreNxt(),Matching();
		printf("%ld\n",ans.size());
		far(i,ans)printf("%lld\n",i);
		return;
	}
}

[HNOI2008]GT考試

思路

設 $f_{i,j}$ 表示准考證的後 $i$ 位中的前 $j$ 位匹配上了 $A$ 的方案數。答案顯然為：

\[\sum_{i=1}^{m}f_{n,i} \]

發現不好轉移，那麼我們再新增一個 $g_{i,j}$ 表示匹配上前 $i$ 位時通過加數位匹配上 $j$ 位的方案數。

此時轉移方程顯然為：

\[f_{i,j}=\sum_{k=1}^{m}f_{i,k}\times g_{k,j} \]

媽呀這不就是矩陣乘法嗎？

媽呀這個 $g$ 陣列不是確定的嗎？

媽呀這衝個矩陣快速冪不就行了嗎？

所以現在我們只需要考慮如何求 $g$ 陣列即可。

其實這個也很簡單，我們只需要列舉下一個數位，找到長度為 $j$ 的字首失配後跳到那個字首上才能匹配成功即可。

時間複雜度 $\Theta(m^3\log_2n)$。

程式碼

點選檢視程式碼

const ll N=30,inf=1ll<<40;
ll n,m,P,nxt[N],ans;char s[N];
class Matrix{
public:
	ll a[N][N];
	inline ll* operator[](ll x){return a[x];}
	inline void Clear(){memset(a,0,sizeof(a));}
	inline void One(){_for(i,1,m)a[i][i]=1;}
	inline Matrix operator*(Matrix mat){
		Matrix ans;ans.Clear();
		_for(i,1,m)_for(j,1,m)_for(k,1,m)
			ans[i][j]=(ans[i][j]+a[i][k]*mat[k][j]%P)%P;
		return ans;
	}
}f,g;
namespace SOLVE{
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	inline void GetNxt(){
		ll j=0;
		_for(i,2,m){
			while(j&&s[j+1]!=s[i])j=nxt[j];
			if(s[j+1]==s[i])++j;
			nxt[i]=j;
		}
		return;
	}
	inline void Pre(){
		_for(i,0,m-1){
			_for(j,'0','9'){
				ll k=i;
				while(k&&s[k+1]!=j)k=nxt[k];
				if(s[k+1]==j)++k;
				++g[i+1][k+1],g[i+1][k+1]%=P;
			}
		}
		return;
	}
	inline Matrix fpow(Matrix a,ll b){
		Matrix ans;ans.Clear(),ans.One();
		while(b){
			if(b&1)ans=ans*a;
			a=a*a,b>>=1;
		}
		return ans;
	}
	inline ll GetAnswer(){
		f.Clear(),f[1][1]=1;
		g=fpow(g,n),f=f*g;
		_for(i,1,m)ans=(ans+f[1][i])%P;
		return ans;
	}
	inline void In(){
		n=rnt(),m=rnt(),P=rnt();
		scanf("%s",s+1);
		GetNxt(),Pre();
		printf("%lld\n",GetAnswer());
		return;
	}
}

Trie

Phone List

思路

模板題。

程式碼

點選檢視程式碼

const ll N=1e6+10,inf=1ll<<40;
ll T,n,ans;char s[N];
class Trie{
private:
	ll tot=1;
	class TRIE{public:ll nx[20];bool en=0;}tr[N];
public:
	inline void Clear(){tot=1,memset(tr,0,sizeof(tr));return;}
	inline bool Add(char *s){
		ll len=strlen(s+1),q1=0,q2=0;
		ll p=1;
		_for(i,1,len){
			ll c=s[i]-'0';
			if(!tr[p].nx[c])q1=1,tr[p].nx[c]=++tot;
			p=tr[p].nx[c],q2|=tr[p].en;
		}
		tr[p].en=1;
		return (!q1)||(q2);
	}
}tr;
namespace SOLVE{
	inline ll rnt(){
		ll x=0,w=1;char c=getchar();
		while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
		return x*w;
	}
	inline void In(){
		n=rnt(),ans=0;
		_for(i,1,n){
			scanf("%s",s+1);
			ans|=tr.Add(s);
		}
		puts(ans?"NO":"YES");
		tr.Clear();
		return;
	}
}

The XOR Largest Pair

思路

01-Trie 模板題。

首先我們把所有數化成二進位制數，從高位到低位塞進 01-Trie 裡。

然後計算答案，有如下兩種方式：

法一（較為通用）：

對於每個數，我們都在根據它的二進位制數在 01-Trie 上儘量反著走，互斥或出的結果一定是包含它的所有數對中最大的，再取個 $\max$ 就能得到答案了。

時間複雜度是穩的 $\Theta(n\log_2n)$。
法二（自創，不通用）：遞迴實現。傳入兩個節點，然後分情況討論：
- 兩個節點都沒有兒子了：直接退出並返回當前算出的答案。
- 兩個節點都只有一個兒子且都指向 $0$ 或都指向 $1$：都往這個兒子處走，且這一二進位制位答案為 $0$。
- 兩個節點中有一個有兒子指向 $1$，另一個節點有一個有兒子指向 $0$：往這兩個兒子處走，且這一二進位制位答案為 $1$。
最後返回的答案就是了（見程式碼）。

可以發現最壞情況下要跑滿整棵樹，但很多情況下跑不滿，而且樹也填不到 $\Theta(n\log_2n)$ 級別，所以時間複雜度嚴格小於 $\Theta(n\log_2n)$，跑得飛快。

程式碼

點選檢視程式碼

const ll N=5e6+10,inf=1ll<<40;
ll n,a[N];
class Trie{
public:
	ll tot=1;
	class TRIE{public:ll nx[2];}tr[N];
	inline void Add(ll num){
		stack<bool>st;
		_for(i,1,31)st.push(num&1),num>>=1;
		ll p=1;
		while(!st.empty()){
			if(!tr[p].nx[st.top()])tr[p].nx[st.top()]=++tot;
			p=tr[p].nx[st.top()];
			st.pop();
		}
		return;
	}
	inline ll Solve(ll lp,ll rp,ll num){
		ll ans=0;
		if(!tr[lp].nx[0]&&!tr[lp].nx[1]&&!tr[rp].nx[0]&&!tr[rp].nx[1])ans=num;
		if(!tr[lp].nx[0]&&tr[lp].nx[1]&&!tr[rp].nx[0]&&tr[rp].nx[1])ans=Solve(tr[lp].nx[1],tr[rp].nx[1],num<<1);
		if(tr[lp].nx[0]&&!tr[lp].nx[1]&&tr[rp].nx[0]&&!tr[rp].nx[1])ans=Solve(tr[lp].nx[0],tr[rp].nx[0],num<<1);
		if(tr[lp].nx[0]&&tr[rp].nx[1])ans=max(ans,Solve(tr[lp].nx[0],tr[rp].nx[1],num<<1|1));
		if(tr[lp].nx[1]&&tr[rp].nx[0])ans=max(ans,Solve(tr[lp].nx[1],tr[rp].nx[0],num<<1|1));
		return ans;
	}
}tr;
namespace SOLVE{
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	inline ll rnt(){
		ll x=0,w=1;char c=gc();
		while(!isdigit(c)){if(c=='-')w=-1;c=gc();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=gc();
		return x*w;
	}
	inline void In(){
		n=rnt();
		_for(i,1,n)a[i]=rnt(),tr.Add(a[i]);
		printf("%lld\n",tr.Solve(1,1,0));
		return;
	}
}

The XOR-longest Path

思路

互斥或和有一個重要性質：$a\oplus b\oplus b=a$。

那麼兩個節點 $u$ 和 $v$ 之間的路徑互斥或和就相當於 $u$ 到根的互斥或和互斥或上 $v$ 到根的互斥或和（因為這兩次中 $u$ 和 $v$ 的 $\text{LCA}$ 到根的互斥或和會被互斥或沒）。

於是問題就轉化成了：找到兩個節點 $u$ 和 $v$，使它們到根的互斥或和的互斥或和最大。

那麼把每個點到根的互斥或和預處理出來，就變成上一道題了。

程式碼

點選檢視程式碼

const ll N=1e6+10,inf=1ll<<40;
ll n,a[N],ans;vector<pair<ll,ll> >tu[N];
class Trie {
private:
	ll tot=1;
	class TRIE{public:ll nx[2];}tr[N];
public:
	#define nx(p,i) tr[p].nx[i]
	inline void Add(ll num){
		ll p=1;stack<ll>st;
		_for(i,1,31)st.push(num&1),num>>=1;
		while(!st.empty()){
			if(!nx(p,st.top()))nx(p,st.top())=++tot;
			p=nx(p,st.top()),st.pop();
		}
		return;
	}
	ll Solve(ll lp,ll rp,ll num){
		ll ans=0;
		if(!nx(lp,0)&&!nx(lp,1)&&!nx(rp,0)&&!nx(rp,1))ans=num;
		if(nx(lp,0)&&!nx(lp,1)&&nx(rp,0)&&!nx(rp,1))ans=Solve(nx(lp,0),nx(rp,0),num<<1);
		if(!nx(lp,0)&&nx(lp,1)&&!nx(rp,0)&&nx(rp,1))ans=Solve(nx(lp,1),nx(rp,1),num<<1);
		if(nx(lp,0)&&nx(rp,1))ans=max(ans,Solve(nx(lp,0),nx(rp,1),num<<1|1));
		if(nx(lp,1)&&nx(rp,0))ans=max(ans,Solve(nx(lp,1),nx(rp,0),num<<1|1));
		return ans;
	}
	#undef nx
}tr;
namespace SOLVE {
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	inline ll rnt(){
		ll x=0,w=1;char c=gc();
		while(!isdigit(c)){if(c=='-')w=-1;c=gc();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=gc();
		return x*w;
	}
	void Dfs(ll u,ll fa,ll num){
		tr.Add(num);
		far(pr,tu[u]){
			ll v=pr.first,w=pr.second;
			if(v==fa)continue;
			Dfs(v,u,num^w);
		}
	}
	inline void In(){
		n=rnt();
		_for(i,1,n-1){
			ll u=rnt(),v=rnt(),w=rnt();
			tu[u].push_back(make_pair(v,w));
			tu[v].push_back(make_pair(u,w));
		}
		Dfs(1,0,0);
		printf("%lld\n",tr.Solve(1,1,0));
		return;
	}
}

Nikitosh 和互斥或

思路

剛開始由於我只會我的非主流最大互斥或對寫法，想了好久都不會，後來看了眼題解學會了主流寫法，瞬間就會做了……

設 $l_i$ 表示 $1\sim i$ 中互斥或和最大的一段區間，$r_i$ 表示 $i\sim n$ 中互斥或和最大的一段區間（注意：$i$ 不必須是左/右端點）。

答案顯然是：

\[ans=\max_{i=1}^{n-1}\{l_{i}+r_{i+1}\} \]

那麼如何求 $l_i$ 和 $r_i$ 呢？

一段區間的互斥或和一定是該區間左右端點各自的字首/字尾互斥或和的互斥或和，那麼我們預處理出所有前/字尾互斥或和，再對每一個左/右端點查詢包含它自己的最大互斥或對即可。

程式碼

點選檢視程式碼

const ll N=4e5+10,M=N<<5,inf=1ll<<40;
ll n,a[N],sum1[N],sum2[N],l[N],r[N],ans;
class Trie{
private:
	ll tot=1;
	class TRIE{public:ll nx[2];}tr[M];
public:
	inline void Add(ll num){
		stack<ll>st;ll p=1;
		_for(i,1,31)st.push(num&1),num>>=1;
		while(!st.empty()){
			if(!tr[p].nx[st.top()])tr[p].nx[st.top()]=++tot;
			p=tr[p].nx[st.top()],st.pop();
		}
		return;
	}
	inline ll Find(ll num){
		stack<ll>st;ll p=1,ans=0;
		_for(i,1,31)st.push(num&1),num>>=1;
		while(!st.empty()){
			if(tr[p].nx[st.top()^1])p=tr[p].nx[st.top()^1],ans=ans<<1|(st.top()^1);
			else p=tr[p].nx[st.top()],ans=ans<<1|st.top();
			st.pop();
		}
		return ans;
	}
}tr1,tr2;
namespace SOLVE{
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	inline ll rnt(){
		ll x=0,w=1;char c=gc();
		while(!isdigit(c)){if(c=='-')w=-1;c=gc();}
		while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=gc();
		return x*w;
	}
	inline void In(){
		n=rnt(),tr1.Add(0),tr2.Add(0);
		_for(i,1,n)a[i]=rnt();
		_for(i,1,n){
			sum1[i]=sum1[i-1]^a[i],tr1.Add(sum1[i]);
			l[i]=max(l[i-1],tr1.Find(sum1[i])^sum1[i]);
		}
		for_(i,n,1){
			sum2[i]=sum2[i+1]^a[i],tr2.Add(sum2[i]);
			r[i]=max(r[i+1],tr2.Find(sum2[i])^sum2[i]);
		}
		_for(i,1,n-1)ans=max(ans,l[i]+r[i+1]);
		printf("%lld\n",ans);
		return;
	}
}

\[\Huge\mathfrak{The\ End} \]

「學習筆記」字串基礎：Hash，KMP與Trie

「學習筆記」字串基礎：Hash，KMP與Trie

Hash

演演算法

程式碼

KMP

演演算法

前置知識：\(\text{Border}\)

思路

程式碼

\(\text{KMP}\) 匹配

思路

程式碼

Trie

資料結構

01-Trie

程式碼

練習題

Hash

思路

程式碼

思路

程式碼

思路

程式碼

KMP

思路

程式碼

思路

程式碼

思路

程式碼

思路

程式碼

思路

程式碼

思路

程式碼

Trie

思路

程式碼

思路

程式碼

思路

程式碼

思路

程式碼