浮點數儲存方式
在檢視記憶體會發現 int i = 1 在記憶體中儲存的就是 00 00 00 01,而儲存 float i=12.5 在記憶體中的表示 41 48 00 00,檢視這個16進位制很明顯這個浮點數不是通過直接轉換得來的,而是通過一些規則的計算規則得來的,這裡就引出了 IEEE 規範了,需要了解這個規範的朋友可以去網上查查,我這邊就說明下轉換方法,我在下面挑了幾個特例來進行說明下。
12.5轉16進位制
計算整數部分
12轉換為16進位制 0xC 轉換成二進位制 1100。
整數部分等於 1100。
計算小數部分
將小數部分進行乘以 2 如果出現整數那麼就為 1 沒有整數就為 0 一致計算到沒有小數為止。
0.5 * 2 = 1.0
通過上面計算,一次計算後小數就為 0 了,所有最終結果就為 1 。
計算指數
將上計算出來整數部分 1100 跟小數部分 1 進行拼接得到 1100.1,同得到得拼接結果進行計算指數,指數是通過左移或者右移小數點得到的,具體多久左移多久右移請觀察下面的表格。
| 資料 | 移動方式 | 指數 | 最終結果 |
|---|---|---|---|
| 1100.1 | 左移 | 3 | 1.1001 |
| 10001000.101 | 左移 | 7 | 1.0001000101 |
| 0.00101 | 右移 | -3 | 1.01 |
觀察上面表格資料我們可以總結出,是左移還是右移是先看小數點左邊是否存在 1 ,存在就進行左移,不存在就進行右移,具體移動多少位,是由移動到小數點左邊只有一個 1 為止,移動的位數就是 指數 ,向左邊移動 指數 就為正數,向右邊移動 指數 就為負數。
通過上面的規則得到的指數為 3 ,計算指數後的結果為 1.1001。
計算
計算完指數得到的結果 1.1001,指數為 3。
浮點數佔用 32 位,第1位是符號位,2 ~ 9位是整數位,10 ~ 32位元為小數位,下面紅色表示符號位、藍色表示整數位、紫色表示小數位。
0 0000 0000 0000 0000 0000 0000 0000 000
符號位計算
正數符號位 0,負數符號位為 1。
結果
0 0000 0000 0000 0000 0000 0000 0000 000
小數計算
直接將計算完指數的結果中的小數部分填寫進小數部分。
上面計算得到的小數部分就是 1001
結果
0 0000 0000 1001 0000 0000 0000 0000 000
整數計算
將計算 指數 + 127 得到的數轉為16進位制,寫入到整數部分。
127 + 3 = 130轉為16進位制0x82得到二進位制資料 1000 0010。
結果
0 1000 0010 1001 0000 0000 0000 0000 000
最終結果
二進位制形式
0100 0001 0100 1000 0000 0000 0000 0000
16進位制形式
0x41480000
17.4轉16進位制
下面轉換我這邊會提跟 12.5 轉換的差異,很多和轉化一樣的東西就不細寫了。
計算整數部分
17 轉為16進位製得到 11,二進進位製表現形式 0001 0001。
計算小數部分
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0
通過上面可以發現該小數部分,按照規則計算出現了迴圈,所以浮點數需要指定精度,我們這邊就儲存8位元就可以了,那結果就為 0110 0110。
計算指數
0001 0001 + 0110 0110 = 0001 0001.0110 0110
通過觀察拼接結果,需要左移 4 位,最終得到資料 1.000101100110,指數 4。
計算
計算完指數得到的結果 1.000101100110,指數為 4。
符號位計算
0 0000 0000 0000 0000 0000 0000 0000 000
小數計算
0 0000 0000 0001 0110 0110 0000 0000 000
整數計算
127 + 4 = 131,轉為16進位制 0x83 ,二進位制體現形式 1000 0011
0 1000 0011 0001 0110 0110 0000 0000 000
最終結果
二進位制形式
0100 0001 1000 1011 0011 0000 0000 0000
16進位制形式
0x418b3000
第三方轉換結果
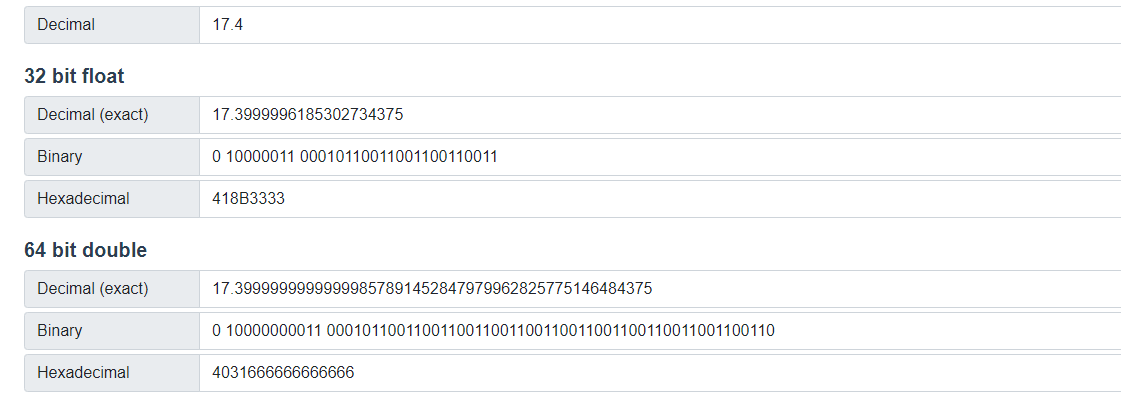
第三轉換結果是 418B3333 和我們計算出的結果存在差異,是因為我們在計算小數部分的只計算了 8 位,因為對 0.4 進行計算的時候,它的小數位計算是無限迴圈的。
-0.6轉16進位制
計算整數部分
整數為 0 那結果就為0。
計算小數部分
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
又出現了迴圈,我這邊就保留 8 位了,那結果等於 1001 1001
計算指數
0 + 10011001 = 0.10011001
這裡可以發現上面的資料左右沒有 1 了,那就需要進行右了,最終移動完後資料 1.0011001 ,指數為 -1。
計算
計算完指數得到的結果 1.0011001,指數為 -1。
符號位計算
1 0000 0000 0000 0000 0000 0000 0000 000
由於當前資料是負數,那符號位就是 1 。
小數計算
1 0000 0000 0011 0010 0000 0000 0000 000
整數計算
127 + (-1) = 126,轉為16進位制 0x7E ,二進位制體現形式 0111 1110。
1 0111 1110 0011 0010 0000 0000 0000 000
最終結果
二進位制形式
1011 1111 0001 1001 0000 0000 0000 0000
16進位制形式
0xbf190000
總結
通過上面的幾個例子,計算浮點數的步驟可以分為一下幾步:
拆分浮點數: 將浮點數拆分為符號部分、整數部分、小數部分。
轉換整數部分: 將整數部分轉化成二進位制,為計算提供準備。
轉換小數部分: 按照轉換規則轉換,將小數部分轉換為二進位制,為計算提供準備。
指數計算: 這一步特別重要,但是隻需要記住左邊有 1 就是左移,移動到左邊只有一個 1 為只,移動的位數就是指數,並且左移指數為正數,右移指數為負數。
小數計算: 直接將小數部分放入小數的位數上。
正數計算: 127 + 指數,就是整數資料。
符號位計算: 正數為 0 ,負數為 1 。