WebGPU的計算著色器實現氣泡排序
大家好~本文使用WebGPU的計算著色器,實現了奇偶排序。
奇偶排序是氣泡排序的並行版本,在1996年由J Kornerup提出。它解除了每輪冒泡間的序列依賴以及每輪冒泡內部的序列依賴,使得冒泡操作可以並行執行
最終版本的程式碼在這裡
介紹奇偶排序演演算法
假設待排序的陣列為Arr1
在奇數步中,Arr1中奇數項與相鄰的右邊一項比較和交換;
在偶數步中,Arr1中奇數項與相鄰的左邊一項比較和交換;
直到一步中沒有交換項,則停止
舉例來說的話,如下圖所示:

在每步中,紅框內的兩項進行比較和交換;
直到一步中沒有交換項,則停止
分析時間複雜度
與氣泡排序一樣,總的比較次數不變,依然為O(n^2)次
但因為為並行執行,所以時間複雜度降低為O(log2(n^2))=O(n)
需求
排序的需求如下所示:
- 對一個包含128個數位的陣列進行升序的排序
初步設計
因為陣列可以兩兩分為64個組,每個組並行執行操作,所以計算著色器只使用一個workgroup,包含64個區域性單位,每個區域性單位對應一個組;
在每個區域性單位中:
啟動一個while迴圈,執行每步操作,然後同步,最後判斷所有區域性單位在該步驟中是否有交換操作,如果都沒有的話則停止迴圈
「執行每步操作」時判斷該步驟是奇數還是偶數步,從而取對應的兩項來比較和交換
程式碼實現
經過上面的設計後,現在我們來實現程式碼
計算著色器程式碼如下所示:
//64個區域性單位
const workgroupSize = 64;
// 區域性單位之間的共用變數,用於存放128個數位
var<workgroup> sharedData: array<f32,128>;
// 區域性單位之間的共用變數,用於標誌所有區域性單位在該步驟中是否有交換操作(只要有任意一個區域性單位在該步驟中有交換操作,則該標誌為true)
var<workgroup> isSwap: bool;
// 區域性單位之間的共用變數,用於記錄步驟數,從而判斷是奇數還是偶數步
var<workgroup> stepCount: u32;
struct BeforeSortData {
data : array<f32, 128>
}
struct AfterSortData {
data : array<f32, 128>
}
//待排序的陣列
@binding(0) @group(0) var<storage, read> beforeSortData : BeforeSortData;
//排序後的陣列
@binding(1) @group(0) var<storage, read_write> afterSortData : AfterSortData;
@compute @workgroup_size(workgroupSize, 1, 1)
fn main(
@builtin(global_invocation_id) GlobalInvocationID : vec3<u32>,
) {
//將待排序的資料讀取到共用變數中
var index = GlobalInvocationID.x * 2;
sharedData[index] = beforeSortData.data[index];
sharedData[index+ 1 ] = beforeSortData.data[index + 1];
//初始化共用變數
isSwap = false;
stepCount = 0;
//同步
workgroupBarrier();
//開始迴圈
while(true){
var firstIndex:u32;
var secondIndex:u32;
//判斷該步驟是奇數還是偶數步,從而得到對應的兩項的序號
//偶數步
if(stepCount % 2 == 0){
firstIndex = index + 1;
secondIndex = index + 2;
}
//奇數步
else{
firstIndex = index;
secondIndex = index + 1;
}
//確保沒超過邊界
if(secondIndex < 128){
//將大的一項交換到後面,從而實現升序
if(sharedData[firstIndex] > sharedData[secondIndex]){
var temp = sharedData[firstIndex];
sharedData[firstIndex] = sharedData[secondIndex];
sharedData[secondIndex] = temp;
isSwap = true;
}
}
stepCount += 1;
workgroupBarrier();
//如果該步驟中沒有交換操作的話則停止迴圈
if(!isSwap){
break;
}
}
//將排序後的資料傳給返回給CPU端的Storage Buffer中,從而可在CPU端得到排序後的結果
afterSortData.data[index] = sharedData[index];
afterSortData.data[index + 1] = sharedData[index + 1];
}
本來我是想像設定workgroupSize一樣,將128設為const的,如下所示:
const workgroupSize = 64;
const itemCount = 128;
var<workgroup> sharedData: array<f32,itemCount>;
但是執行時會報錯!照理說根據WGSL的檔案,是不應該報錯的!所以不清楚是我沒搞清楚還是WGSL目前的bug?
(另外,如果使用override而不是const,也會報錯!)
如果改為使用workgroupSize,則不會報錯。程式碼如下所示:
const workgroupSize = 64;
var<workgroup> sharedData: array<f32,workgroupSize>;
這是因為workgroupSize在@workgroup_size中使用了。程式碼如下所示:
@compute @workgroup_size(workgroupSize, 1, 1)
發現問題
執行程式碼後,會報錯:
1 warning(s) generated while compiling the shader:
:74:5 warning: 'workgroupBarrier' must only be called from uniform control flow
workgroupBarrier();
^^^^^^^^^^^^^^^^
:77:5 note: control flow depends on non-uniform value
if(!isSwap){
^^
:77:9 note: reading from workgroup storage variable 'isSwap' may result in a non-uniform value
if(!isSwap){
^^^^^^
這是因為WGSL會進行Uniformity analysis檢查,確保像「workgroupBarrier」這種barries是在uniform control flow中安全地呼叫
WGSL在檢查時發現:因為isSwap被多個區域性單位讀寫,所以為"non-uniform value",導致所在的control flow為non-uniform,從而報錯
更多關於Uniformity的資料在這裡:
uniformity
Add the uniformity analysis to the WGSL spec
uniformity issues
改進設計
現在需要去掉isSwap的if判斷
因為isSwap的if判斷是用來結束迴圈的,那麼在去掉它之後我們就需要新的結束條件
因為總共有128個數位要排序,所以最多進行128步即可完成所有的排序
相關程式碼實現
所以去掉isSwap,把迴圈終止條件修改下,並且重構一下程式碼
相關程式碼改為:
fn _swap(firstIndex:u32, secondIndex:u32){
var temp = sharedData[firstIndex];
sharedData[firstIndex] = sharedData[secondIndex];
sharedData[secondIndex] = temp;
}
fn _oddSort(index:u32) {
var firstIndex = index;
var secondIndex = index + 1;
if(sharedData[firstIndex] > sharedData[secondIndex]){
_swap(firstIndex, secondIndex);
}
}
fn _evenSort(index:u32) {
var firstIndex = index + 1;
var secondIndex = index + 2;
if(secondIndex <128 && sharedData[firstIndex] > sharedData[secondIndex]){
_swap(firstIndex, secondIndex);
}
}
@compute @workgroup_size(workgroupSize, 1, 1)
fn main(
@builtin(global_invocation_id) GlobalInvocationID : vec3<u32>,
) {
...
var firstIndex:u32;
var secondIndex:u32;
for (var i: u32 = 0; i < 128; i += 1) {
//偶數步
if(stepCount % 2 == 0){
_evenSort(index);
}
//奇數步
else{
_oddSort(index);
}
stepCount +=1 ;
workgroupBarrier();
}
...
}
現在就能夠正確執行了
改進設計
現在我們通過判斷步驟數是偶數還是奇數來進行對應的排序,這會造成「Warp Divergence」的優化問題:
不同的區域性單位會進入不同的分支(偶數步或者奇數步),造成同一時刻除了正在執行的分支以外,其餘分支都被阻塞了,十分影響效能
如下圖所示:
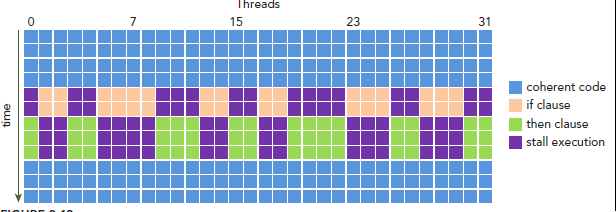
參考資料:
CUDA程式設計——Warp Divergence
所以我們可以去掉stepCount和相關的判斷,改為在每次迴圈中分別執行奇數排序和偶數排序,並把迴圈次數減半
相關程式碼實現
修改後的相關程式碼為:
for (var i: u32 = 0; i < 64; i += 1) {
_oddSort(index);
workgroupBarrier();
_evenSort(index);
workgroupBarrier();
}
限制
現在程式有如下的限制:
- 只有一個workgroup,意味著只能排序最多「區域性單位數量*2」個數位
總結
感謝大家的學習~
計算著色器是SIMT架構,也就是說每條指令都是並行執行的。這與CPU的序列思維不同,所以我們要切換為並行的思維,並在需要同步的時候同步
另外,計算著色器的程式碼因為處在並行環境下,所以需要仔細優化
有下面的一些優化建議:
- 減少Warp Divergence
- 儘量減少if判斷
- if中儘量使用常數判斷,如if(const value < 2)
- 減少Bank Conflict
- 對共用變數記憶體儘量連續地讀寫
如對本文的共用陣列sharedData,儘量連續的讀寫相鄰的序號
- 對共用變數記憶體儘量連續地讀寫
- 減少同步操作
- 如果已知確定的迴圈次數,可以展開回圈,這樣可以減少同步操作和迴圈的指令開銷
參考資料
啥是Parallel Reduction
CUDA(六). 從並行排序方法理解並行化思維——冒泡、歸併、雙調排序的GPU實現
uniformity
CUDA程式設計——Warp Divergence


