論文資訊

論文標題：Understanding Attention and Generalization in Graph Neural Networks
論文作者：Boris Knyazev, Graham W. Taylor, Mohamed R. Amer
論文來源：2019,NeurIPS
論文地址：download
論文程式碼：download

1 Introduction

　　本文關注將注意力 GNNs 推廣到更大、更復雜或有噪聲的圖。作者發現在某些情況下，注意力機制的影響可以忽略不計，甚至有害，但在某些條件下，它給一些分類任務帶來了超過 60% 的額外收益。

2 Attention meets pooling in graph neural networks

　　注意力機制可以用在邊上，也可以用在節點上，傳統的 GAT 是用在邊上，本文更關注於節點上的注意力機制。

　　注意力機制在CNN裡一般用以下公式表達：

　　　　$Z=\alpha \odot X  \quad\quad\quad(1)$

　　其中:

• • $X \in \mathbb{R}^{N \times C}$ 代表輸入；
  • $Z_{i}=\alpha_{i} X_{i}$ 是使用注意力機制後的輸出；
  • $\alpha$ 是注意力係數，並有 $\sum_{i}^{N} \alpha_{i}=1$；

　　在 Graph U-Nets​ 的 $\text{Eq.2}$ 中，同樣使用到了注意力機制：

　　　　$Z_{i}=\left\{\begin{array}{ll}\alpha_{i} X_{i}, & \forall i \in P \\\emptyset, & \text { otherwise }\end{array}\right.\quad\quad\quad(2)$

　　其中：

• • $P$ 是一組集合節點的索引，且有 $|P| \leq N$；
  • $\emptyset$ 表示輸出中不存在該單元；

　　本文的 $\text{Eq.2}$ 和 $\text{Eq.1}$ 的不同之處在於，在 Graph U-Nets 中 $Z \in \mathbb{R}^{|P| \times C}$ 表明只使用了部分節點，即儲存了 $r=|P| / N \leq 1$ 部分的節點。

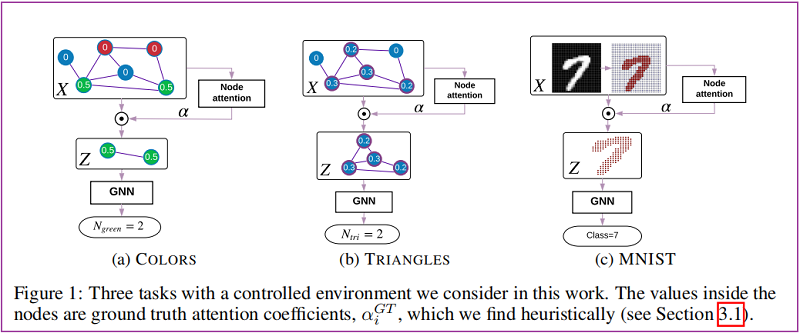
　　本文設計了兩個簡單的圖形推理任務，讓我們在一個受控環境中研究注意力，瞭解地面真實注意力。第一個任務是計算圖中的顏色，其中顏色是一個唯一的離散特徵。第二個任務是計算圖形中的三角形的數量。​我們在一個標準基準，MNIST[13]（Figure1）上證實了我們的觀察結果，並確定了影響注意力有效性的因素。​

3 Model

　　本文研究了兩種GNNs：GCN 和 GIN，其中 GIN 將原有的 MEAN aggregator 替換為 SUM aggregator，然後使用一個 FC 層。

3.1 Thresholding by attention coefficients

　　使用 Graph U-Nets 中的方法，需要使用預定義的比率 $r=|P| / N$  為整個資料集選擇節點。比如對每個 pooling 設定 r = 0.8 即 80% 的節點被儲存下來。直觀地說，對於大小不同的圖，這個比率應該是不同的。因此，建議選擇閾值 $\tilde{\alpha}$，這樣就只傳播具有注意值 $\alpha_{i}>\tilde{\alpha}$ 的節點：

　　　　$Z_{i}=\left\{\begin{array}{ll}\alpha_{i} X_{i}, & \forall i: \alpha_{i}>\tilde{\alpha} \\\emptyset, & \text { otherwise }\end{array}\right. \quad\quad\quad(3)$

　　Note：圖中刪除的節點不同於儲存的節點，其特徵的值是非常小的，甚至為 $0$。在本實驗中，相近鄰域的節點通常有相似 $\alpha$ ，因此整個區域性鄰域被合併或者丟棄，而不是基於聚類的方法將每個鄰域壓縮為單個節點。

3.2 Attention subnetwork

　　為了訓練一個預測節點係數的注意模型，我們考慮了兩種方法：

• • Linear Projection[11]：只有單層投影 $\mathbf{p} \in \mathbb{R}^{C}$ 需要被訓練：$\alpha_{\text {pre }}=X \mathbf{p}​$；
  • DiffPool[10]，其中訓練了一個單獨的 GNN：$\alpha_{\text {pre }}=X \mathbf{p}​$；

　　在所有情況下，我們在[11]中使用 softmax 啟用函數而不是 tanh，因為它提供了更可解釋的結果和稀疏輸出：$\alpha=\operatorname{softmax}\left(\alpha_{p r e}\right)$ 。為了以監督或弱監督的方式訓練注意力，我們使用 KL 散度損失。

3.3 ChebyGIN

　　有些結果下，GCNs 和 GINs 表現的較差，本文將 GIN 和 ChebyNet 進行融合，研究了 $K=2$ 的 ChebyGIN。

4 Experiments

4.1 Datasets

　　本文引入了顏色計數任務，即統計圖中綠色的節點有多少個，對於綠色節點設定 注意力係數為 $\alpha_{i}^{G T}=1 / N_{\text {green }}$。

TRIANGLES

　　統計圖中有多少個三角形？顯然一個簡單 的方法是計算：$\operatorname{trace}\left(A^{3}\right) / 6$ 。

　　接著對每個節點設定注意力係數：$\alpha_{i}^{G T}=T_{i} / \sum\limits _{i} T_{i}$，其中 $T_{i}$ 是多少個三角形包含節點 $i$。

MNIST-75SP

 

　　該任務的目的是識別出圖片代表的數位是多少，其中圖片為 $0-9$ 的數位。具體方法是先用 SLIC 演演算法生成超畫素快，然後構建圖。每個節點對應一個超畫素塊。然後 $\alpha$ 係數的初始值的計算公式為：$\alpha_{i}^{G T}=1 / N_{\text {nonzero }}$ ，$N_{\text {nonzero }}$ 是這些超畫素的總數。

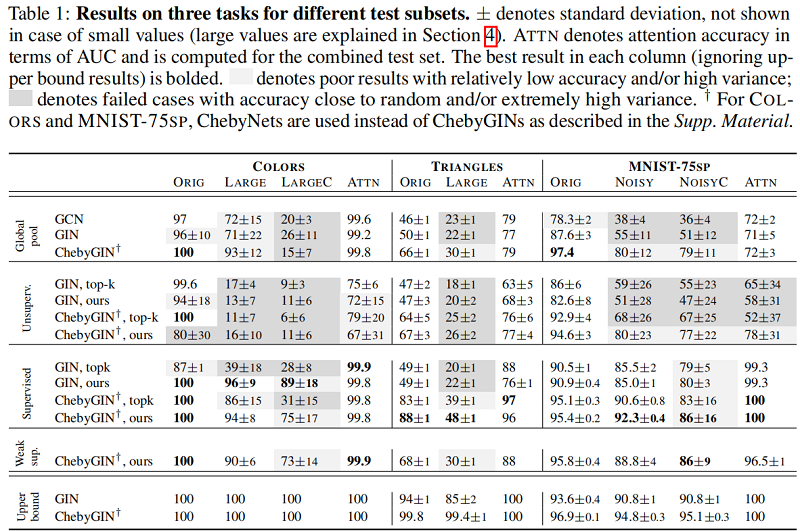
4.2 Generalization to larger and noisy graphs

　　為了驗證注意力機制的健壯性，作者將顏色實驗和三角形實驗引入到更大的網路之中。如圖：

　　

　　在顏色實驗中新增了另外一個通道，變成 $4$ 個通道 [ c_1,c_2,c_3,c_3 ]，然後其中 [0,1,0,0] 的時候代表綠色，其他的時候 $[c_1,0,c_3,c_4]$ 其中 $c_1$，$c_3$，$c_4$，可以是 $0-1$ 之間的數值，代表紅色，藍色，透明色的三種顏色的混合。

　　在三角形計數實驗中，也引入了更多的節點數。

　　在MNIST資料集的實驗中，加入了高斯噪音，是的模型的識別度更高。

4.3 Network architectures and training

　　對於 COLORS 和 TRIANGLES，我們最小化了其他任務的迴歸損失(MSE)和交叉熵(CE)，對於有監督和弱監督實驗，本文還最小化了 ground truth attention $\alpha^{G T}$ 和 predicted coefficients $\alpha$ 之間的 KL 散度。

　　　　$\mathcal{L}=\mathcal{L}_{M S E / C E}+\frac{\beta}{N} \sum\limits _{i} \alpha_{i}^{G T} \log \left(\frac{\alpha_{i}^{G T}}{\alpha_{i}}\right)   \quad\quad\quad(5)$

　　為了評估注意力係數的正確性，遵循CNN的方式，我們在訓練完一個模型之後呢，移除這個節點，再計算預測一個標籤，計算與原始標籤的差異，這樣來計算出一個評估的 $\alpha$ 係數：

　　　　$\alpha_{i}^{W S}=\frac{\left|y_{i}-y\right|}{\sum\limits _{j=1}^{N}\left|y_{j}-y\right|}$

5 Experiments

　　

 

6 Conclusion

　　證明了注意力對於圖神經網路是非常強大的，但是由於初始注意力係數的敏感性，要達到最優是很困難的。特別是在無監督的環境中，由於不能確定初始注意力係數的值，使得這樣的訓練更加困難。我們還表明，注意力可以使GNN對更大，更嘈雜的圖形有更強的能力。同時本文提出的弱監督模型和有監督模型具有相似的優勢性。