完全二元樹

完全二元樹的定義

滿二元樹

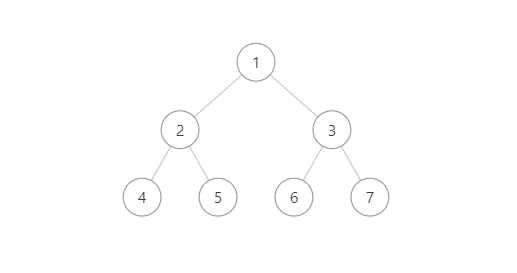
非完全二元樹，非滿二元樹

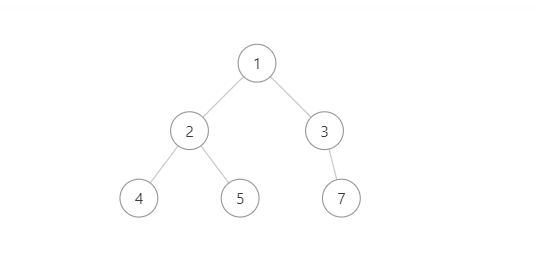
完全二元樹

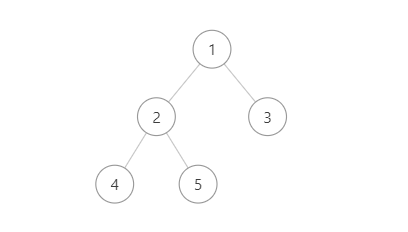
完全二元樹的特點

葉子結點只能出現在最下層和次下層，且最下層的葉子結點集中在樹的左部。

完全二元樹的實現

二元連結串列：直觀，但佔用記憶體大。
陣列：簡潔，但拓展麻煩。

比較推薦使用陣列儲存，本文也將基於陣列儲存介紹大頂堆的實現。

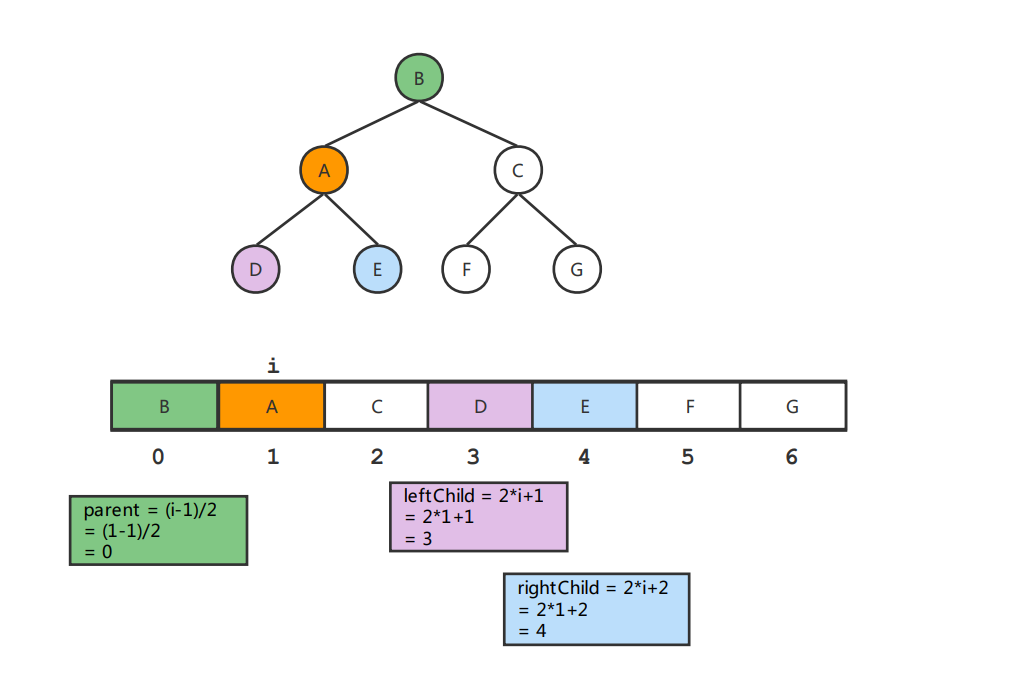
基於陣列儲存的完全二元樹節點與陣列下標的關係

假設完全二元樹的 節點 A 儲存在陣列中的下標為 i
則：

節點 A 的父節點儲存在陣列中的下標為 (i - 1) / 2
節點 A 的左子節點儲存在陣列中的下標為 2 * i + 1
節點 A 的右子節點儲存在陣列中的下標為 2 * i + 2

堆

堆的定義

堆是一種特殊的資料結構，是高效的優先順序佇列，堆通常可以被看做一棵完全二元樹。

堆的分類

根據堆的特點，可以把堆分為兩類：

大頂堆：每一個節點的值都大於或等於其左右子節點的值。
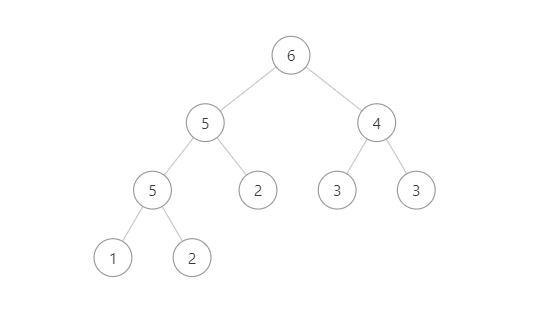
小頂堆：每一個節點的值都小於或等於其左右子節點的值。

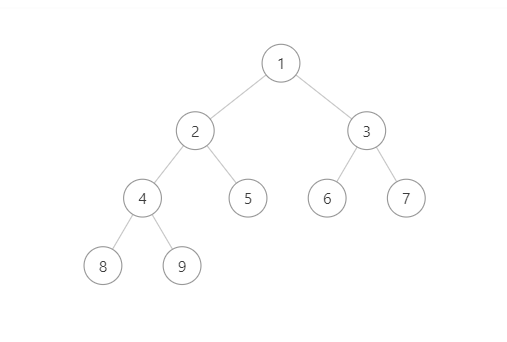
堆的插入

往堆中插入資料，可能會破壞大頂堆（小頂堆）的性質，需要對堆進行調整。
堆的插入流程如下：

將插入的資料置於陣列的尾部
將新插入的節點作為當前節點，比較當前節點與其父節點是否滿足堆的性質，不滿足則交換
重複步驟 2，直到滿足堆的性質或者當前節點到達堆頂。

/**
 * 新增元素
 * @param value 待新增元素
 */
public void offer(int value){
  if(this.currentLength >= this.capacity){    // 陣列已耗盡，擴增陣列為原來的兩倍
    this.grow();
  }
  int cur = this.currentLength++;             // 獲得待新增元素的新增位置
  if(cur == 0){                               // 當前堆為空直接新增
    this.tree[cur] = value;
  }else{                                      // 當前堆不為空，新增之後要向上調整
    this.tree[cur] = value;                   // 步驟 1
    int p = cur;                            
    int parent = this.getParentIndex(p);    
    while(this.tree[parent] < this.tree[p]){  // 步驟 2
      this.swap(parent, p);
      p = parent;
      parent = this.getParentIndex(p);
    }
  }
}

往堆中插入資料的時間複雜度為 O(logN)

堆的構建

構建一個大小為 N 的堆，其實就是執行 N 次插入。
所以構建一個大小為 N 的堆，其時間複雜度為 O(NlogN)

堆的刪除

堆的刪除也可能會破壞大頂堆（小頂堆）的性質，需要對堆進行調整。
堆的刪除流程如下：

取出堆頂的資料
用堆的最後一個元素代替堆頂元素
判斷當前節點（一開始是堆頂），是否滿足大頂堆（小頂堆）的性質，不滿足則用左右子節點中較大的節點進行交換
重複步驟 3 直到滿足堆的性質或沒有子節點

/**
 * 取出最大元素
 * @return 最大元素
 */
public int poll(){
    if(isEmpty()){
        throw new RuntimeException("堆為空，無法取出更多元素！");
    }
    int cur = --this.currentLength;         // 獲得當前堆尾
    int result = this.tree[0];              // 取出最大元素 步驟1
    this.tree[0] = this.tree[cur];          // 將堆尾移到堆頭 步驟2
    if(cur != 0){                           // 如果取出的不是最後一個元素，需要向下調整堆 步驟3
        int p = 0;
        int left = getLeftIndex(p);
        int right = getRightIndex(p);
        // 由於是陣列實現，陣列元素無法擦除，需要通過邊界進行判斷堆的範圍
        // 當前節點和左節點在堆的範圍內，
        while(p < this.currentLength &&
                0 <= left && left < this.currentLength &&
                (this.tree[left] > this.tree[p] || this.tree[right] > this.tree[p])){
            if(right >= this.currentLength){    // 當前節點沒有右節點
                if(this.tree[left] > this.tree[p] ){        // 左節點大於當前節點
                    swap(p, left);
                    p = left;
                }
            }else{                                          // 兩個節點都在堆範圍
                if(this.tree[left] > this.tree[right]){     // 用大的節點替換
                    swap(p, left);
                    p = left;
                }else{
                    swap(p, right);
                    p = right;
                }
            }
            left = getLeftIndex(p);
            right = getRightIndex(p);
        }
    }
    return result;
}

堆的刪除元素時間複雜度為 O(logN)

完整程式碼

// 大頂堆
public class Heap {
    private int[] tree;         // 陣列實現的完全二元樹
    private int capacity;       // 容量
    private int currentLength;  // 當前陣列已使用長度

    /**
     * 建構函式
     * @param capacity 初始容量
     */
    public Heap(int capacity) {
        this.tree = new int[capacity];
        this.capacity = capacity;
        this.currentLength = 0;
    }

    /**
     * 新增元素
     * @param value 待新增元素
     */
    public void offer(int value){
        if(this.currentLength >= this.capacity){    // 陣列已耗盡，擴增陣列為原來的兩倍
            this.grow();
        }
        int cur = this.currentLength++;             // 獲得待新增元素的新增位置
        if(cur == 0){                               // 當前堆為空直接新增
            this.tree[cur] = value;
        }else{                                      // 當前堆不為空，新增之後要向上調整
            this.tree[cur] = value;                 // 步驟 1
            int p = cur;
            int parent = this.getParentIndex(p);
            while(this.tree[parent] < this.tree[p]){    // 步驟 2
                this.swap(parent, p);
                p = parent;
                parent = this.getParentIndex(p);
            }
        }
    }

    /**
     * 取出最大元素
     * @return 最大元素
     */
    public int poll(){
        if(isEmpty()){
            throw new RuntimeException("堆為空，無法取出更多元素！");
        }
        int cur = --this.currentLength;         // 獲得當前堆尾
        int result = this.tree[0];              // 取出最大元素 步驟1
        this.tree[0] = this.tree[cur];          // 將堆尾移到堆頭 步驟2
        if(cur != 0){                           // 如果取出的不是最後一個元素，需要向下調整堆 步驟3
            int p = 0;
            int left = getLeftIndex(p);
            int right = getRightIndex(p);
            // 由於是陣列實現，陣列元素無法擦除，需要通過邊界進行判斷堆的範圍
            // 當前節點和左節點在堆的範圍內，
            while(p < this.currentLength &&
                    0 <= left && left < this.currentLength &&
                    (this.tree[left] > this.tree[p] || this.tree[right] > this.tree[p])){
                if(right >= this.currentLength){    // 當前節點沒有右節點
                    if(this.tree[left] > this.tree[p] ){        // 左節點大於當前節點
                        swap(p, left);
                        p = left;
                    }
                }else{                                          // 兩個節點都在堆範圍
                    if(this.tree[left] > this.tree[right]){     // 用大的節點替換
                        swap(p, left);
                        p = left;
                    }else{
                        swap(p, right);
                        p = right;
                    }
                }
                left = getLeftIndex(p);
                right = getRightIndex(p);
            }
        }
        return result;
    }

    public boolean isEmpty(){
        return this.currentLength <= 0;
    }

    private int getParentIndex(int index){
        return (index - 1) / 2;
    }

    private int getLeftIndex(int index){
        return 2 * index + 1;
    }

    private int getRightIndex(int index){
        return 2 * index + 2;
    }

    private void swap(int left, int right){
        int temp = this.tree[left];
        this.tree[left] = this.tree[right];
        this.tree[right] = temp;
    }

    /**
     * 將陣列拓展為原來的兩倍
     */
    private void grow(){
        this.tree = Arrays.copyOf(this.tree, 2 * currentLength);
        this.capacity = this.tree.length;
    }
}

大頂堆的實現（基於陣列儲存的完全二元樹）