Excel函數學習之LOOKUP函數的二分法原理

手機如何做表格：點選檢視

在之前的文章中，咱們學習了LOOKUP函數的各種套路，也多次提到了LOOKUP函數的查詢是根據二分法來進行的，那麼到底什麼是二分法，今天就來聊聊這個問題。

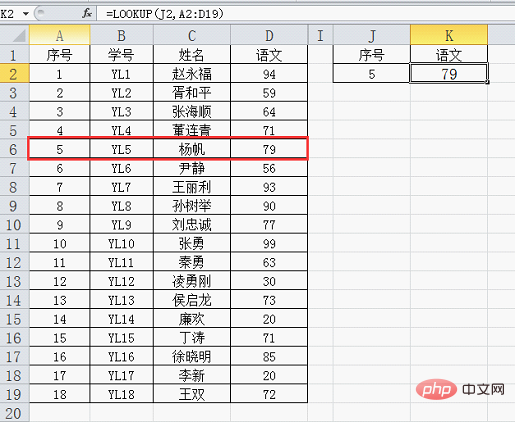
還是用昨天的例子：按序號查詢成績，序號是升序排列的，公式=LOOKUP(J2,A2:D19)的結果正確。

一、二分法查詢原理

二分法查詢是把查詢範圍中的資料按照個數一分為二找到位於中間位置的一個資料，中間值，然後用我們的查詢值和中間值做比較。當中間值等於查詢值時，直接去獲取結果；當中間值小於查詢值時，則向下繼續進行二分法查詢比較（也就是在不含中間值在內的下方的那一半資料中繼續進行二分法查詢）；當中間值大於查詢值時，則向上繼續進行二分法查詢比較（也就是在不含中間值在內的上方的那一半資料中繼續進行二分法查詢）。如果如此二分到最後一個資料都未找到等於查詢值的資料：最後一個資料小於查詢值的，那就以最後一個資料的位置去獲取結果值；最後一個資料大於查詢值的，那就再向上找一個位置最靠近最後一個資料的小於或等於查詢值的資料，再以這個資料的位置去獲取結果。

只是這樣解釋估計很多朋友都會犯迷糊，我們結合上面的例子，具體看看如何通過序號5，找到語文成績79的。

第一次比較：查詢範圍A2~A19一共18個資料，中間位置是18÷2=9，即中間值是A10單元格的9。顯然查詢值5小於9，所以繼續向上在A2~A9中查詢；

提示：如果查詢範圍資料個數是單數，中間位置就是（個數+1）÷2，例如11行的話，中間位置就是（11+1）÷2=6；如果資料個數是偶數，中間位置就是（個數）÷2。

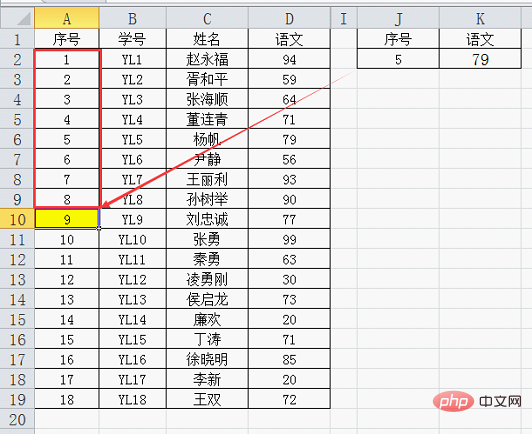
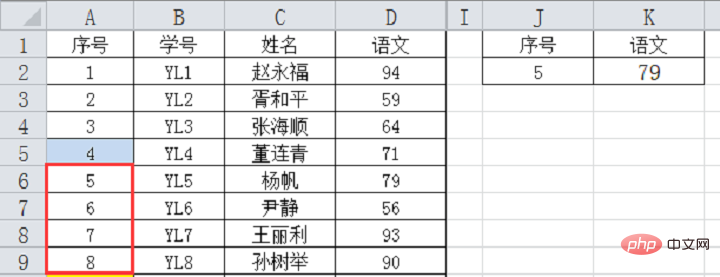
第二次比較：只有8個資料，中間位置是8÷2=4，中間值是A5單元格的4，查詢值5大於4，所以繼續向下在A6~A9中找。注意此時下面只有四個數，第一次查詢時直接將9下面的資料都排除了。

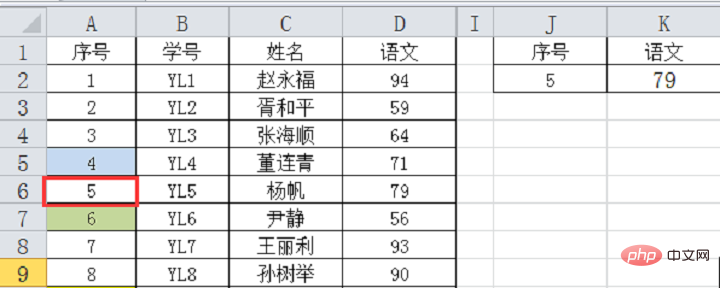
第三次比較：4個資料，中間值是A7的6，查詢值5小於6，所以向上找。此時只剩下一個資料A6單元格的5，與查詢值一致，因此就得到5所對應的D列資料79。

僅僅通過這樣一個例子要想明白二分法是很困難的，我們再看一個例子。將上表中的資料按照成績降序排列，還是按序號5查詢語文成績，公式不做修改。因為序號這一列的順序亂了，不是升序排列，結果就出現了錯誤，實際是79，公式得到的是94，這是怎麼回事呢？還是通過二分法來看看吧。

第一次查詢：中間值（第9個資料）是18，查詢值5小於18，因此向上在A2~A9中找；

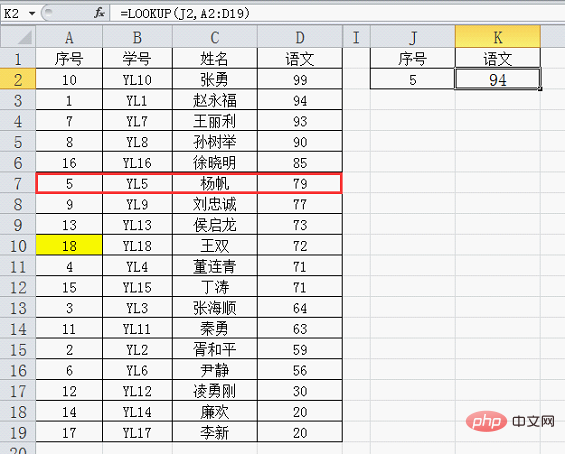
第二次查詢：上面的8個資料，中間值（第4個資料）是8，查詢值5小於8，繼續向上在A2~A4中找；

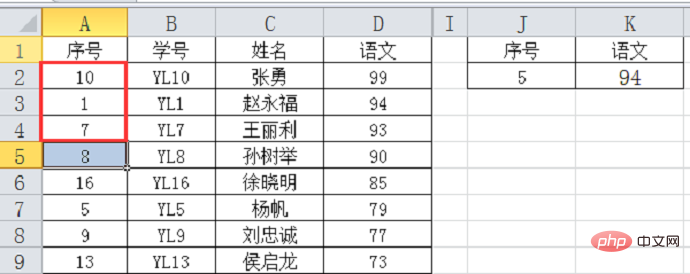
第三次查詢：上面的3個資料，中間值是1，查詢值5大於1，向下找：

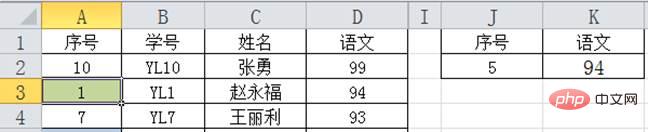
第四次查詢：現在只有A4單元格一個資料7，查詢值5小於7，因此以7為參考，向上找一個位置最靠近7，同時數值小於5或者等於5的資料，即A3單元格的1，由此獲得對應的語文值就是94。

通過這兩個例子，我想大家對於二分法應該有了一定的認識，關於這個原理，在函數說明裡只有一句話的介紹：

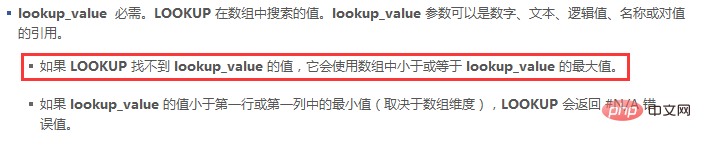
在實際應用中，我們可以不用去糾結二分法到底是怎麼回事，中間位置是什麼，該往下還是往上找，這都是函數的工作，我們只需要記住一點：資料一定要升序排列，如果不能升序排列，那麼就按照LOOKUP的精確查詢套路去設計公式。

二、LOOKUP實現資料的四捨五入

二分法原理就介紹這麼多，接下來需要解決之前遺留的兩個問題。

在5月12日的文章中，我們用LOOKUP解決了一個四捨五入的問題，結果大家紛紛留言要個解釋：

那麼引起大家熱議的這個公式到底是什麼呢？看下圖：

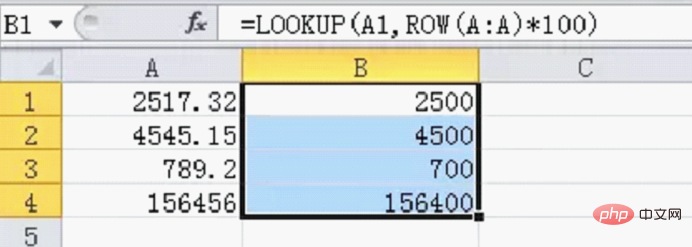
原來這個公式是用LOOKUP函數將一個數位百位以下全部捨去，實現了百分位取整。

在瞭解過二分法原理以後，是時候讓LOOKUP還大家一個解釋了。首先說明ROW（A:A）*100這部分。它其實就是得到了一組數位。為了讓大家看明白，把A:A範圍給小一點，我們用=ROW(A1:A31)*100作說明：

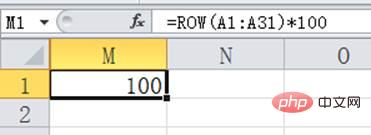
雖然單元格中只能看到一個100，實際上是31個數位，我們可以用f9功能鍵來看看具體內容：

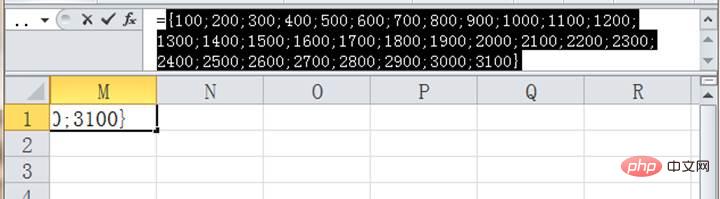
ROW函數用於獲取單元格的行號，ROW(A1:A31)*100就是用A1到A31單元格的行號分別乘以100，得到一組百位取整的資料{100;200;300;……3000;3100}。

然後LOOKUP上場了。它要在上述得到的已經百位取整的陣列中查詢A1。因為陣列是按升序排列的，所以查詢A1的實質就是在陣列中找小於等於A1的最大值。

以2517.32為例，唯有2500是小於它的最大值，因此結果就是2500。有興趣的朋友可以自己用二分法原理去試試，看看對不對。

其他數位的查詢方式都是如此。這個公式之所以巧妙，就是把一個四捨五入的問題變成了查詢參照的問題，真是妙！

三、LOOKUP進行資料提取

我們又利用LOOKUP進行資料的提取，因此有了一個5000字的約會：

這次又是什麼問題呢？原題如圖所示提取學號：

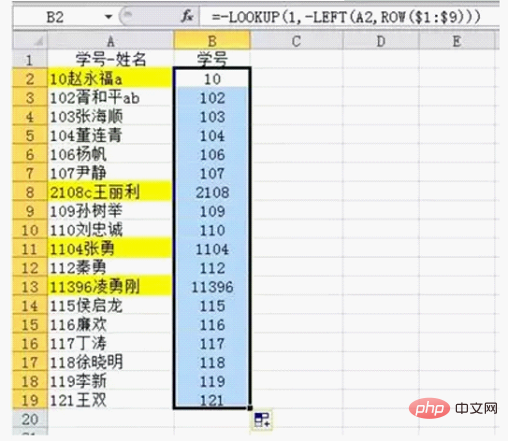
咱們用上圖的第一個資料來解釋。在N1單元格中輸入「10張勇a」，然後在O1單元格中輸入公式=-LOOKUP(1,-LEFT(N1,ROW(1:9)))提取學號。

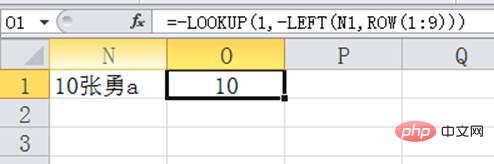
LOOKUP不是參照函數嗎，怎麼又可以提取數位了？

LEFT函數的第二個引數使用了一個陣列，ROW(1:9)相當於{1;2;3;4;5;6;7;8;9}。LEFT是把第一引數指定的資料從左邊開始提取，提取的長度由第二引數來確定。 LEFT按照陣列{1;2;3;4;5;6;7;8;9}提取，得到9個結果：

也就是從左邊開始提取1位，2位……一直到9位。因為LEFT提取的結果都是文字型別，在LEFT前面加上負號，就可以把其中的文字型數位轉為數值，文字變成錯誤值：

錯誤值被LOOKUP忽略，現在就變成了在{-1; -10}中找1。1比這組資料都大，根據二分法查詢原理，二分後只能向下找，直到最後一位小於1的資料。因此，我們可以簡單理解成：當查詢值大於查詢範圍中所有資料（不管是否是升序排列）時，LOOKUP的實質就是在找最後一個資料。

其實將公式中的1變成0也是可以的，因為0也比所有的負數大：

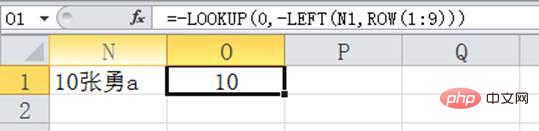
當前最後一個數是-10，所以我們在LOOKUP前面再加個負號，就變成10了，也就是我們需要提取的數位。

對於初學者來說，以上兩個案例中LOOKUP的用法過於高階，即便是通過這些介紹，估計也是一知半解，其實學習函數是有一個過程的，從不認識到了解，從瞭解再到掌握，這裡需要大量的練習和思考。只要大家保持積極樂觀的心態，能夠體會到學習函數的樂趣的時候，就離成功不遠了。

相關學習推薦：

以上就是Excel函數學習之LOOKUP函數的二分法原理的詳細內容，更多請關注TW511.COM其它相關文章！