論文資訊

論文標題：Graph U-Nets
論文作者：Hongyang Gao, Shuiwang Ji
論文來源：2019,ICML
論文地址：download 
論文程式碼：download 

1 Introduction

　　受到類似 encoder-decoder architecture 的 U-Nets 影響，作者希望能在圖資料上使用這種 pooling 和 up-sampling 的操作。

2 Graph U-Nets

　　本節依次介紹 graph pooling (gPool) layer， graph unpooling (gUnpool) layer，然後介紹本文用於節點分類的 U-Nets 。

2.1 Graph Pooling Layer

　　本文提出利用投影向量  $\mathbf{p}$  來計算圖中各個節點的重要性，並且  $\mathbf{p}$  是可訓練的引數，不需要認為指定。假設節點的嵌入向量為  $\mathbf{x}_{\mathrm{i}}$ , 它在向量  $\mathbf{p}$  上的投影為  $\mathrm{y}_{\mathrm{i}}=\mathbf{x}_{\mathrm{i}} \mathbf{p} /\|\mathbf{p}\|$， $\mathrm{y}_{\mathrm{i}}$  可以作為衡量節點重要性的度量。

　　$\mathrm{gPool}$ 計算過程為：

　　　　$\begin{array}{l}\mathbf{y} &=&X^{\ell} \mathbf{p}^{\ell} /\left\|\mathbf{p}^{\ell}\right\| \\\mathrm{idx} &=&\operatorname{rank}(\mathbf{y}, k) \\\tilde{\mathbf{y}} &=&\operatorname{sigmoid}(\mathbf{y}(\mathrm{idx})) \\\tilde{X}^{\ell} &=&X^{\ell}(\mathrm{idx},:) \\A^{\ell+1} &=&A^{\ell}(\mathrm{idx}, \mathrm{idx}) \\X^{\ell+1} &=&\tilde{X}^{\ell} \odot\left(\tilde{\mathbf{y}} \mathbf{1}_{C}^{T}\right)\end{array}$

　　圖示如下：

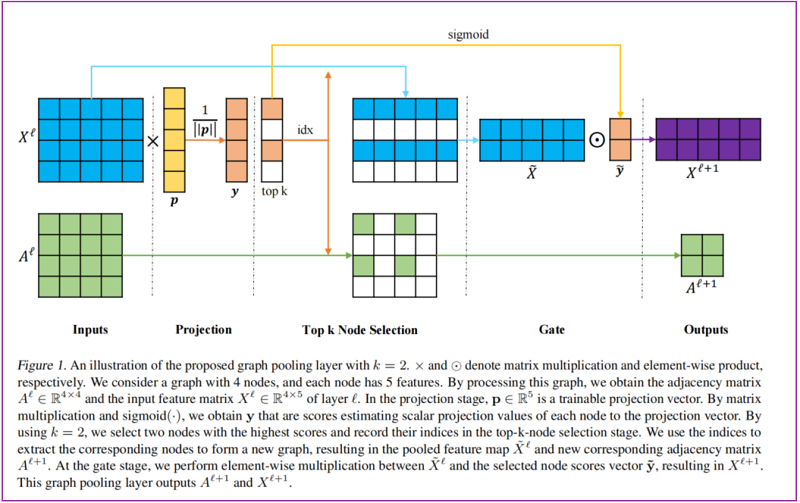
2.2 Graph Unpooling Layer

　　為在圖資料上實現 up-sampling 操作，本文提出 graph unpooling (gUnpool) layer。

　　

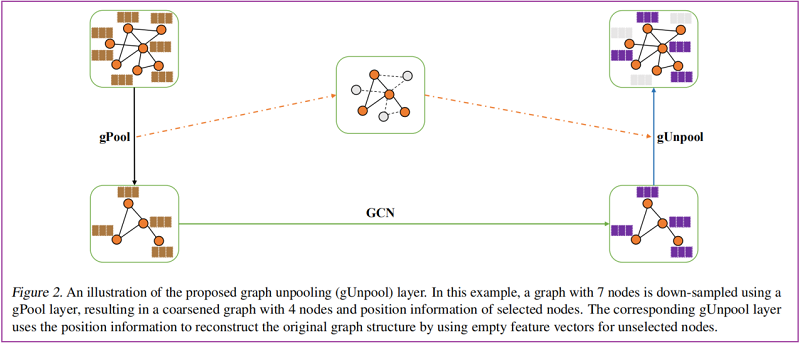
　　在形式上，gUnpool 的層級傳播規則為：

　　　　$X^{\ell+1}=\operatorname{distribute}\left(0_{N \times C}, X^{\ell}, \mathrm{idx}\right)$

　　其中，

• • $idx \in \mathbb{Z}^{* k}$ 包含在相應的 gPool 層中所選節點的索引，從而將圖的大小從 $N$ 個節點減少到 $k$ 個節點；
    
  • $X^{\ell} \in \mathbb{R}^{k \times C}$ 是當前圖的特徵矩陣；
    
  • $0_{N \times C}$ 是新圖的 0 填充的特徵矩陣；
    

　　Note：在 $X^{\ell+1}$ 中，$idx$ 中具有索引的行向量由 $X^{\ell}$ 中的行向量更新，而其他行向量保持為零。

2.3 Graph U-Nets Architecture

　　如圖所示：

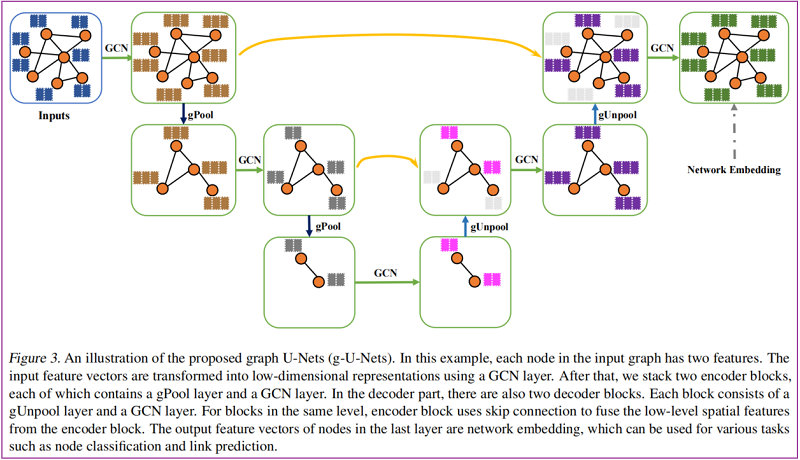
2.4 Graph Connectivity Augmentation via Graph Power

　　在 gPool 層中，對一些重要的節點進行取樣，形成一個新的特徵編碼圖。由於在刪除 gPool 中的節點時相關邊被刪除，所以 pooled graph 中可能形成孤立點。可能會影響資訊在後續層中的傳播，特別是當使用 GCN 層來聚合來自鄰近節點的資訊時。所以需要增加 pooled graph 中節點之間的連通性。

　　為了解決上述問題，使用第 $k$ 個圖的冪 $\mathbb{G}^{k}$ 來增加圖的連通性。文中使用 $k = 2$ ，替換計算過程中的 $A^{\ell+1}$：

　　　　$A^{2}=A^{\ell} A^{\ell}, \quad A^{\ell+1}=A^{2}(\mathrm{idx}, \mathrm{idx})$

2.5 Improved GCN Layer

　　在  $\mathrm{GCN}$  中鄰接矩陣  $\hat{\mathrm{A}}=\mathrm{A}+\mathrm{I}$ , 論文中改為  $\hat{\mathrm{A}}=\mathrm{A}+2 \mathrm{I}$，給予中心節點更大的權重。

3 Experimental Study

資料集

節點分類

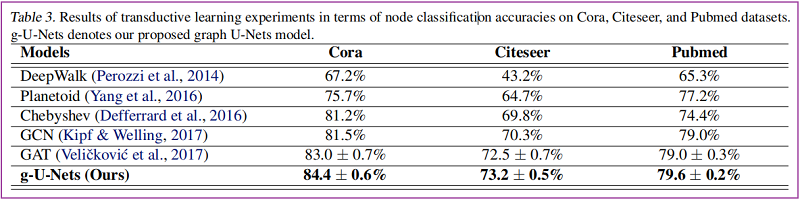
圖分類

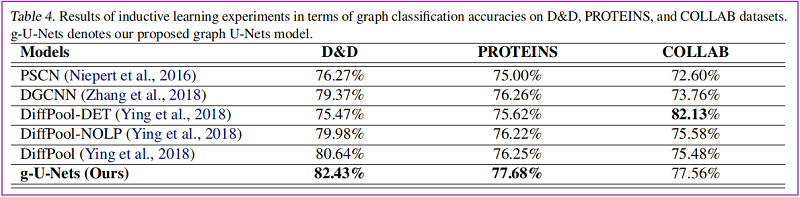
4 Conclusion

　　在這項工作中，我們提出了g-U-Nets網路中新的 gPool 和 gUnpool 層用於網路嵌入。gPool 層對圖形資料實現了規則的全域性 k-max 池化操作。它對重要節點的子集進行取樣，以實現高階特徵編碼和接受域擴大。通過使用一個可訓練的投影向量，gPool層根據其標量投影值對節點進行取樣。此外，我們提出了對圖資料應用非池操作的gUnpool層。利用原圖中節點的位置資訊，gUnpool 層對相應的 gPool 層進行逆操作，恢復原圖的結構。基於我們的 gPool 和 gUnpool 層，我們提出了圖 U-Nets(gU-Nets) 結構，它在影象資料上使用與常規U-Net類似的編碼-解碼器結構。實驗結果表明，與其他gnn相比，我們的g-u-net在轉換學習任務上實現了效能的提高。為了避免取樣圖中可能存在的孤立節點問題，我們採用第二圖冪來提高圖的連通性。對消融術的研究表明了這些貢獻