論文資訊

論文標題：DropEdge: Towards Deep Graph Convolutional Networks on Node Classification
論文作者：Yu Rong, Wenbing Huang, Tingyang Xu, Junzhou Huang
論文來源：2020, ICLR
論文地址：download
論文程式碼：download

1 Introduction

　　由於 2022 年的論文看不懂，找了一篇 2020 的論文緩解一下心情，我太難了。

　　提出一種可以緩解過擬合、過平滑的策略，並且和其他 backbone 模型組合將得到更好的效能。

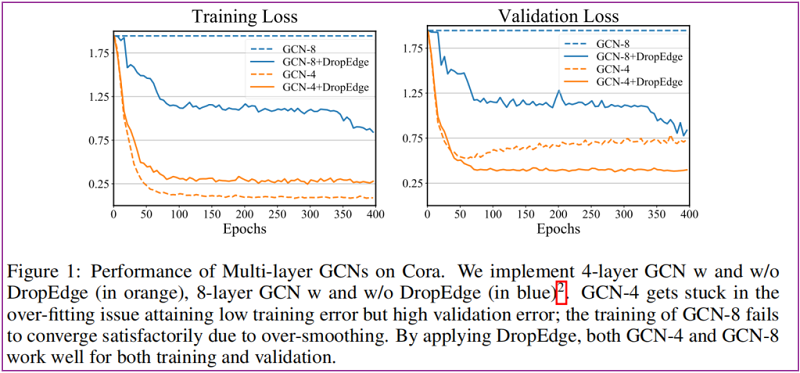
　　驗證小圖上容易出現過平滑現象：參見 Figure 1 Cora 資料集上使用 8 層 GCN 的結果。

　　DropEdge 主要思想是：在每次訓練時，隨機刪除掉原始圖中固定比例的邊。

　　在GCN訓練過程中應用DropEdge有許多好處：

DropEdge 可以看成是資料增強技術。在訓練過程中對原始圖中的邊進行不同的隨機刪除，也就增強了輸入資料的隨機性和多樣性，可以緩解過擬合的問題。
DropEdge 還可以看成是一個訊息傳遞減少器。GCNs中，鄰接節點間的訊息傳遞是通過連邊實現的，隨機刪除掉一些邊就可以讓節點連線更加稀疏，在一定程度上避免了GCN層數加深引起的過平滑問題。

2 Preliminary

GCN

　　前向傳播層為：

　　　　$\boldsymbol{H}^{(l+1)}=\sigma\left(\hat{\boldsymbol{A}} \boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}\right)\quad\quad\quad(1)$

　　其中，$\hat{\boldsymbol{A}}=\hat{\boldsymbol{D}}^{-1 / 2}(\boldsymbol{A}+\boldsymbol{I}) \hat{\boldsymbol{D}}^{-1 / 2}$，$\boldsymbol{W}^{(l)} \in \mathbb{R}^{C_{l} \times C_{l-1}}$。

3 Method

3.1 Methodlogy

　　在每個訓練 epoch，DropEdge 技術隨機刪除輸入圖的一定邊。形式上，它隨機地強制鄰接矩陣 $A$ 的 $V_p$ 非零元素為零，其中 $V$ 是邊的總數，$p$ 是丟棄率。如果我們將得到的鄰接矩陣表示為 $A_{drop}$，那麼它與 $A$ 的關係就變成了

　　　　$A_{\mathrm{drop}}=A-A^{\prime}\quad\quad\quad(2)$

　　其中 $\boldsymbol{A}^{\prime}$ 是原始圖中刪除的邊集，然後對 $\boldsymbol{A}_{\text {drop }}$ 進行 re-normalization 得到 $\hat{\mathbf{A}}_{\text {drop }}$ ，替換 $\text{Eq.1}$ 中的 $\hat{\mathbf{A}}$。

Preventing over-fitting

　　DropEdge 對圖中的連線帶來了擾動，它對輸入資料產生了不同的隨機變形，可以看成是資料增強。

　　GCNs 的核心思想是對每個節點的鄰居特徵進行加權求和，實現對鄰居資訊的聚合。那麼 DropEdge 可以看成在 GNN 訓練時使用的是隨機的鄰居子集進行聚合，而沒有使用所有的鄰居。若 DropEdge 刪邊率為 $p$，對鄰居聚合的期望是由 $p$ 改變的，在對權重進行歸一化後就不會再使用 $p$。

Layer-Wise DropEdge

　　上述所說的是每個 epoch ，GNN 各層共用一個 $\boldsymbol{A}_{\text {drop }}$ 但每層也可以單獨進行 DropEdge，為資料帶來更多的隨機性。

　　Note：同樣，類似的還有可以為每層單獨計算 KNN graph。

　　下文將闡述 DropEdge 如何緩解過平滑問題，並且假設使用的所有層將共用一個 $\boldsymbol{A}_{\text {drop }}$。

3.2 Preventing over-smoothing

　　過平滑原始定義：平滑現象意味著隨著網路深度的增加，節點特徵將收斂到一個固定的點。這種不必要的收斂限制了深度GCNs的輸出只與圖的拓撲相關，但與輸入節點特徵無關，這會損害 GCNs 的表達能力。

　　通過考慮非線性和折積濾波器的思想，可以將過平滑解釋為收斂到子空間，而不是收斂到不動點，本文將使用子空間概念來更具普遍性。

　　首先給出如下定義：

　　根據 Oono & Suzuki 的結論，足夠深的GCN在一些條件下，對於任意小的 $\epsilon$ 值，都會有 $ \epsilon-smoothing$ 問題。他們只是提出了深度 GCN 中存在 $\epsilon-smoothing$，但是沒有提出對應的解決方法。

- 降低節點之間的連線，可以降低過平滑的收斂速度；
- 原始空間和子空間的維度之差衡量了資訊的損失量；

　　即：

4 Discussions

DropEdge vs. Dropout

　　Dropout 試圖通過隨機設定特徵維數為零來干擾特徵矩陣，可能會減少過擬合的影響，但對防止過平滑沒有幫助，因為它不會對鄰接矩陣做出任何改變；
　　DropEdge 可以看成 Dropout 向圖資料的推廣，將刪除特徵換成刪除邊，兩者是互補關係；

DropEdge vs DropNode

　　DropNode 取樣子圖進行小批次訓練，可被視為刪除邊的一種特定形式，因為連線到刪除節點的邊也被刪除。然而，DropNode 對刪除邊的影響是面向節點的和間接的。

　　DropEdge 是面向邊的，並且可以保留訓練的所有節點特徵，表現出更多的靈活性。

　　當前的 DropNode 方法中的取樣策略通常是低效的，例如，GraphSAGE 的層大小呈指數增長，而 AS-GCN 需要逐層遞迴地進行取樣。然而，DropEdge 既不隨著深度的增長而增加圖層的大小，也不要求遞迴程序，因為所有邊的取樣都是平行的。

DropEdge vs Graph-Sparsification

　　圖稀疏化(1997) 的優化目標是去除圖壓縮的不必要的邊，同時保留輸入圖的幾乎所有資訊。這和 DropEdge 的目的一樣，但不同的是 DropEdge 不需要具體的優化目標，而圖稀疏化則採用一種繁瑣的優化方法來確定要刪除哪些邊，一旦這些邊被丟棄，輸出圖將保持不變。

5 Experiment

資料集

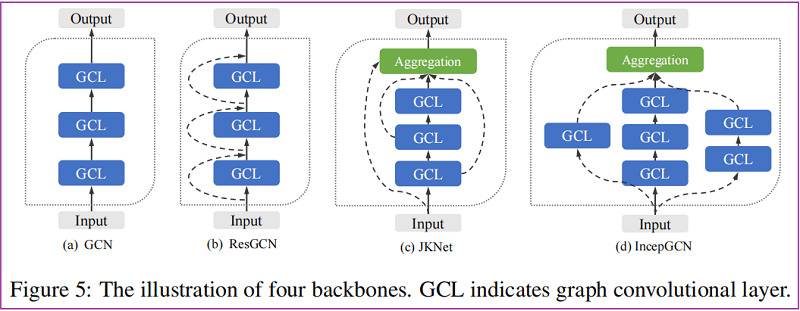
Backbones

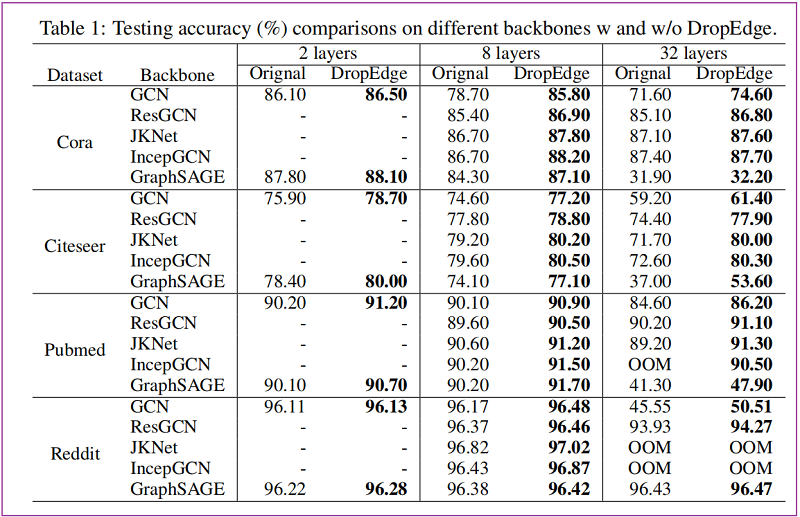
節點分類：（監督學習）

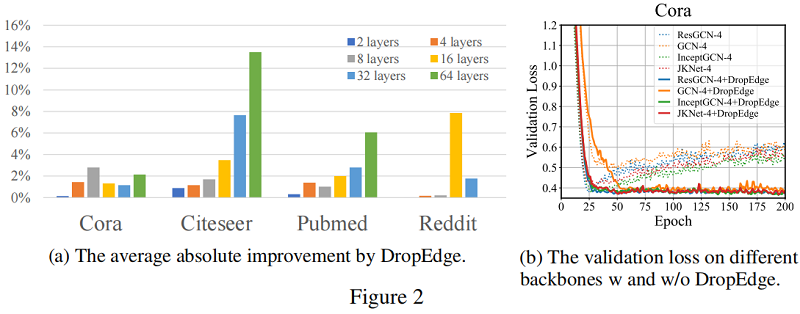
驗證損失

標準化/傳播模型

6 Conclusion

　　DropEdge 在輸入資料中包含了更多的多樣性，以防止過擬合，並減少了圖折積中的訊息傳遞，以緩解過平滑。

論文解讀（DropEdge）《DropEdge: Towards Deep Graph Convolutional Networks on Node Classification》