Bellman-Ford演演算法與SPFA演演算法詳解

PS：如果您只需要Bellman-Ford/SPFA/判負環模板，請到相應的模板部分

上一篇中簡單講解了用於多源最短路的Floyd演演算法。本篇要介紹的則是用與單源最短路的Bellman-Ford演演算法和它的一些優化（包括~~已死的~~SPFA）

Bellman-Ford演演算法

其實，和Floyd演演算法類似，Bellman-Ford演演算法同樣是基於DP思想的，而且也是在不斷的進行鬆弛操作（可以理解為「不斷放寬對結果的要求」，比如在Floyd中就體現為不斷第一維\(k\)，具體解釋在這裡)

既然是單源最短路徑問題，我們就不再需要在DP狀態中指定起始點。於是，我們可以設計出這樣的DP狀態（和Floyd很類似）：

\[dp[k][u]表示從s（起點）到u，最多經過k條邊時的最短路徑 \]

顯然，初始值為：

\[對於起點s，dp[0][s]=0；對於其他任意節點u，dp[0][u]=+\infin \]

我們可以先考慮，如何從\(dp[0][u]\)轉移出\(dp[1][u]\)（就是多一條邊）。

於是很容易想到這個最顯而易見~~又最暴力~~的方法：列舉每一條邊\((u, v)\)，並更新\(dp[1][v]=min(dp[1][v], dp[0][u]+w[u][v])（其中w[u][v]表示這條邊的邊權）\)

推廣到任意\(dp[k-1][u]\)到\(dp[k][u]\)的轉移，我們仍然可以使用這樣的方法。

下面是程式碼實現：

struct Edge {
	int u, v; // 邊的兩個端點
	int w; // 邊的權值
};

int n; // 點數
int m; // 邊數
Edge e[MAXM]; // 所有的邊
int dp[MAXN][MAXN]; // 解釋見上方

void bellman_ford(int start) {
	memset(dp, 0x3f, sizeof(dp)); // 初始化為INF
	dp[0][start] = 0;
	for(int i = 1; i < n; i++) { // 一張圖中的最長路徑最多隻包含n - 1邊，所以更新n - 1遍就夠了（因為點不能重複）
		for(int j = 1; j <= n; j++) { // 先複製一遍
			dp[i][j] = dp[i - 1][j];
		}
		for(int j = 1; j <= m; j++) { // 列舉每一條邊
			dp[i][e[j].v] = min(dp[i][e[j].v], dp[i - 1][e[j].u] + e[j].w);
		}
	}
}

顯然，時間複雜度為\(O(nm)\)，空間複雜度也是\(O(nm)\)，~~程式碼複雜度為O(1)~~。

我們可以先考慮優化空間複雜度（壓縮掉第一維\(k\)），於是，DP狀態變為：

\[dp[u]表示從s（起點）到u的最短路徑 \]

轉移方程為：

\[dp[v]=min(dp[v],dp[u]+w[v]) \]

關於狀態壓縮後的正確性：最有可能令人不理解的部分就是：在同一輪更新中，我們可能會用已經更新完的值再去更新別的值。這就導致，同一論更新中，不同節點被更新到的DP值對應的\(k\)可能不同。（如果沒看懂，就看下面這張圖）

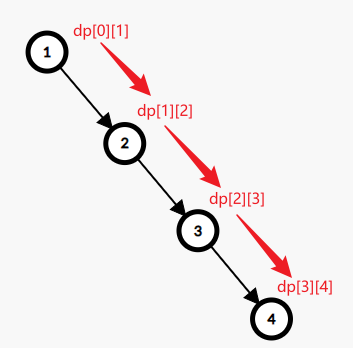
但是實際上，我們其實並不關心到底走了幾步，而只關心最短路的邊權和。所以，像這樣的「錯位更新」並不會引起錯誤。

於是，我們可以得到新的程式碼：

struct Edge {
	int u, v; // 邊的兩個端點
	int w; // 邊的權值
};

int n; // 點數
int m; // 邊數
Edge e[MAXM]; // 所有的邊
int dp[MAXN]; // 解釋見上方

void bellman_ford(int start) {
	memset(dp, 0x3f, sizeof(dp)); // 初始化為INF
	dp[start] = 0;
	for(int i = 1; i < n; i++) { // 一張圖中的最長路徑最多隻包含n - 1邊，所以更新n - 1遍就夠了（因為點不能重複）
		for(int j = 1; j <= m; j++) { // 列舉每一條邊
			dp[e[j].v] = min(dp[e[j].v], dp[e[j].u] + e[j].w);
		}
	}
}

我們可以繼續考慮優化時間複雜度。顯然，如果在某一輪的更新後，發現並沒有任何一個值被更新，那麼就意味著：這張圖已經不能再被更新了（已經求出\(s\)到每個點的最短路），那就可以直接break了。

所以，優化後的程式碼如下：

Bellman-Ford演演算法模板

struct Edge {
	int v; // 邊指向的節點
	int w; // 邊的權值
};

int n; // 點數
int m; // 邊數
vector<Edge> g[MAXN]; // 儲存從每個節點發出的邊
int dp[MAXN]; // 解釋見上方

void bellman_ford(int start) {
	memset(dp, 0x3f, sizeof(dp)); // 初始化為INF
	dp[start] = 0;
	for(int i = 1; i < n; i++) { // 一張圖中的最長路徑最多隻包含n - 1邊，所以更新n - 1遍就夠了（因為點不能重複）
		bool updated = 0; // 記錄是否有節點被更新
		for(int i = 1; i <= n; i++) { // 列舉每一個節點
			if(dp[i] == 0x3f3f3f3f) { // 無法到達的節點
				continue;
			}
			for(Edge &e : g[i]) { // 列舉從這個節點發出的每一條邊
				if(dp[i] + e.w < dp[e.v]) {
					dp[e.v] = dp[i] + e.w;
					updated = 1; // 標記有值被更新
				}
			}
		}
		if(!updated) {
			break; // 沒有節點被更新，直接退出
		}
	}
}

這就是最常見的Bellman-Ford樸素演演算法了。

同時，也可以看到，本次優化後的程式碼中將「直接儲存所有邊」的方式改為了使用「鄰接表」。這是因為鄰接表在圖論演演算法中更加常用，也使得Bellman-Ford演演算法可以更容易地和其他演演算法配合使用。

SPFA演演算法

SPFA演演算法（Shortest Path Faster Algorithm），顧名思義就是一種讓Bellman-Ford跑得更快的方法。

在上一部分的最後，我們對於沒有更新的情況，直接break掉，來優化時間。但是，稍加思考就會發現：有的時候，我們會為了唯一幾個被更新過的節點，而再把所有的節點遍歷一遍，那麼這樣就會產生時間的浪費。所以，SPFA本質上就是使用佇列來解決這樣的問題。

下面是SPFA演演算法的基本步驟：

我們先設定好初始值（和Bellman-Ford一樣），再將起點（\(s\)）加入佇列中。
每次從佇列中取出一個節點，嘗試用它去更新與它相連的節點；如果某個節點的最短距離被更新了，那麼將這個節點加入佇列。
回到步驟2

於是，很容易寫出對應的程式碼：

SPFA演演算法模板

struct Edge {
	int v; // 邊指向的節點
	int w; // 邊的權值
};

int n; // 點數
int m; // 邊數
vector<Edge> g[MAXN]; // 儲存從每個節點發出的邊
int dp[MAXN]; // 定義沒有變
queue<int> q; // 儲存點用的佇列
bool vis[MAXN]; // 記錄每個節點當前是否在佇列中

void spfa(int start) {
	memset(dp, 0x3f, sizeof(dp)); // 初始化為INF
	dp[start] = 0;
	q.push(start);
	vis[start] = 1; // 標記一下
	while(!q.empty()) {
		int x = q.front(); // 取出一個節點
		q.pop();
		vis[x] = 0; // 清除標記，因為下次還有可能入隊
		for(Edge &e : g[x]) { // 列舉從這個節點發出的每一條邊
			if(dp[x] + e.w < dp[e.v]) {
				dp[e.v] = dp[x] + e.w;
				if(!vis[e.v]) { // 如果這個節點現在不在佇列中
					q.push(e.v); // 那就把它加入佇列
					vis[e.v] = 1; // 標記一下
				}
			}
		}
	}
}

一道測試用的例題：P4779 【模板】單源最短路徑（標準版）

Bellman-Ford & SPFA判斷負環

負環，就是邊權和為負數的環。負環是最短路演演算法中一個很重要的問題，因為只要進入一個負環，最短距離就會無限減小。當然，這肯定不是我們希望的，所以接下來就要介紹如何使用Bellman-Ford演演算法或SPFA演演算法來判斷一張圖中是否包含負環。

顯然，一張有向圖上的任意一條簡單路徑最多隻包含\(n-1\)條邊（否則不可能是簡單的）。而且，當圖中沒有負環時，兩點間的最短路徑一定是簡單路徑。所以，如果發現從起點到某個節點\(u\)的最短路徑包含多於\(n-1\)條邊，那麼這條路徑上一定包含負環。

所以，我們只需要在演演算法中新增一些簡單的判斷就可以實現判負環了。

具體方法：

對於普通的Bellman_ford演演算法，我們可以在完成DP後，在進行一遍更新，如果存在任意節點與起點之間的最短路徑是可以被更新的，那麼可以確定圖中一定存在負環
對於SPFA演演算法，我們可以在更新最短路徑的同時，記錄每條最短路徑上的邊數，如果發現某條最短路徑的邊數大於\(n-1\)，那麼可以確定圖中一定存在負環

於是，我們可以寫出分別使用這兩種演演算法來判負環的程式碼：

Bellman-Ford判負環模板

struct Edge {
	int v; // 邊指向的節點
	int w; // 邊的權值
};

int n; // 點數
int m; // 邊數
vector<Edge> g[MAXN]; // 儲存從每個節點發出的邊
int dp[MAXN];

bool bellman_ford_check_ncycle(int start) {
	memset(dp, 0x3f, sizeof(dp)); // 初始化為INF
	dp[start] = 0;
	for(int i = 1; i < n; i++) { // 一張圖中的最長路徑最多隻包含n - 1邊，所以更新n - 1遍就夠了（因為點不能重複）
		bool updated = 0; // 記錄是否有節點被更新
		for(int i = 1; i <= n; i++) { // 列舉每一個節點
			if(dp[i] == 0x3f3f3f3f) { // 無法到達的節點
				continue;
			}
			for(Edge &e : g[i]) { // 列舉從這個節點發出的每一條邊
				if(dp[i] + e.w < dp[e.v]) {
					dp[e.v] = dp[i] + e.w;
					updated = 1; // 標記有值被更新
				}
			}
		}
		if(!updated) {
			return 0; // 沒有節點被更新，一定沒有負環
		}
	}
	for(int i = 1; i <= n; i++) { // 列舉每一個節點
		if(dp[i] == 0x3f3f3f3f) { // 無法到達的節點
			continue;
		}
		for(Edge &e : g[i]) { // 列舉從這個節點發出的每一條邊
			if(dp[i] + e.w < dp[e.v]) {
				return 1; // 還能被更新說明有負環
			}
		}
	}
	return 0;
}

SPFA判負環模板

struct Edge {
	int v; // 邊指向的節點
	int w; // 邊的權值
};

int n; // 點數
int m; // 邊數
vector<Edge> g[MAXN]; // 儲存從每個節點發出的邊
int dp[MAXN]; // dp的定義沒有變
int cnt[MAXN]; // 記錄從起點到節點u的最短路徑中的邊數
queue<int> q; // 儲存點用的佇列
bool vis[MAXN]; // 記錄每個節點當前是否在佇列中

bool spfa_check_ncycle(int start) { // SPFA判負環
	memset(dp, 0x3f, sizeof(dp)); // 初始化為INF
	dp[start] = 0;
	q.push(start);
	vis[start] = 1; // 標記一下
	while(!q.empty()) {
		int x = q.front(); // 取出一個節點
		q.pop();
		vis[x] = 0; // 清除標記，因為下次還有可能入隊
		for(Edge &e : g[x]) { // 列舉從這個節點發出的每一條邊
			if(dp[x] + e.w < dp[e.v]) {
				dp[e.v] = dp[x] + e.w;
				cnt[e.v] = cnt[e.v] + 1; // 多了當前這條邊
				if(cnt[e.v] >= n) { // 從起點到v的最短路徑上有多於n - 1條邊
					return 1; // 一定出現了負環
				}
				if(!vis[e.v]) { // 如果這個節點現在不在佇列中
					q.push(e.v); // 那就把它加入佇列
					vis[e.v] = 1; // 標記一下
				}
			}
		}
	}
	return 0; // 沒有負環
}

一道測試用的例題：P3385 【模板】負環