論文地址：延遲約束的語音增強基音估計

參照格式：Schröter H, Rosenkranz T, Escalante-B A N, et al. LACOPE: Latency-Constrained Pitch Estimation for Speech Enhancement[C]//Interspeech. 2021: 656-660.

---

摘要

　　基頻($f_0$)估計，又稱基音跟蹤，是語音和訊號處理領域長期以來的研究課題。然而，許多基音估計演演算法在噪聲條件下失敗，或者由於其幀大小或Viterbi解碼而引入大延遲。

　　在本研究中，我們提出了一種基於深度學習的基音估計演演算法LACOPE，該演演算法在聯合基音估計和語音增強框架中訓練。與之前的工作相比，該演演算法允許可設定的延遲，最低可達到0的演演算法延遲。這一點是通過利用pitch軌跡的平滑特性實現的。也就是說，一個迴圈神經網路通過預測期望點的pitch來補償由特徵計算引入的延遲，允許在pitch精確度和延遲之間進行權衡。

　　我們將音調估計整合到一個用於助聽器的語音增強框架中。在這個應用中，我們允許 5ms的分析延遲。然後使用基音估計在頻域構建梳狀濾波器，作為後處理步驟，以去除內部諧波噪聲。

　　對於所有噪聲條件下的語音，我們的基音估計效能與PYIN或CREPE等SOTA演演算法相當，同時引入了最小的延遲

索引術語：基音估計，語音增強，折積迴圈神經網路

1  引言

　　消除不需要的環境噪聲是現代助聽器的一個共同特徵。助聽器處理的一個重要特性是整體延遲低，這包括分析、濾波等步驟，如降噪以及合成。特別是對於具有開放耦合的助聽器，原始訊號的強分量到達耳鼓。因此，大於10毫秒的延遲通常是不可取的[1]，因為它們會引入不必要的梳狀濾波器效應(不要與用於內諧波降噪的數位梳狀濾波器混淆)。這些延遲要求導致處理視窗非常短，約為6毫秒，頻寬為500 Hz。由於這種頻率解析度，它不可能減少諧波內噪聲，導致與純淨的語音相比，訊號聽起來更粗糙。為了能夠減弱語音諧波之間的噪聲，最近提出了一個梳狀濾波器[2, 3]。Valin等人[2]用一種基於自相關的方法估計pitch，與OPUS編解碼器[4]類似。然而，這些方法至少要用20毫秒的幀來分析pitch，因此對於我們的延遲限制來說是不可行的。

　　其他基音估計演演算法需要類似的甚至更高的look-ahead。RAPT[5]還使用歸一化互相關（NCC）特徵，結合最大搜尋(maximum search)和動態規劃(dynamic programming)來選擇最佳$f_0$候選。動態規劃通過利用基音的平滑特性提高了魯棒性，因此被許多方法採用[5、6、7、8]。然而，只有在計算Viterbi反向演演算法的至少幾個步驟時，才能利用其全部潛力，這將導致appox的額外延遲。100毫秒[5]。YIN及其概率繼承者PYIN[9，6]使用累積平均歸一化差函數（CMN DF）代替NCC，因為這有助於消除倍頻程誤差。通常，兩者都需要至少20到100ms的幀大小。PYIN需要對動態程式設計進行額外的look-ahead。CREPE[7]是一種基於時域折積的深度學習方法，幀大小為64ms，略優於PYIN。Zhang等人[10]還提出了一種聯合基音估計和語音增強框架。然而，它們僅使用基音特徵作為去噪網路的輸入。

2  訊號模型

　　設$x(k)$是在有噪聲的房間中記錄的混合訊號。

$$公式1：x(k)=s(k)\star h(k)+n(k)$$

式中$s(k)$為純淨語音訊號，$\star $表示折積運算元，$h(k)$為從揚聲器到麥克風的房間脈衝響應(RIR)， $n(k)$為加性噪聲。在訊號模型中加入混響語音$s^{rev}=s(k)\star h(k)$對於泛化現實世界的訊號具有重要意義。此外，混響語音的週期性成分通常略有下降。梳狀濾波器可以通過改善週期性部分來提高感知質量。

　　我們的降噪方法完全適用於頻域。因此，我們使用標準的均勻多相濾波器組(uniform polyphase filter bank)產生以下訊號模型：

$$公式2：X_b(l)=S_b(l)*H_b(l)+N_b(l)$$

其中$b\in \{0...,B-1\}$為頻帶，$l$為幀索引。由於我們對助聽器的實時性要求，分析濾波器組(AFB)大約在6毫秒幀上執行，子取樣率為24。這導致B = 48個波段，頻寬為500 Hz。因此，典型的助聽器降噪演演算法只能衰減整個頻譜包絡，而不能增強語音的週期性部分[11，12]。

　　與[3]類似，我們的降噪演演算法分兩步操作，如圖1所示。首先，通過估計的頻帶增益$G_b$對整個頻譜包絡進行建模，從而得到增強的頻譜圖$\hat{X}_b(l)=X_b(l)G_b(l)$。這還包括通過抑制後期反射來輕微的去混響。接下來，在頻域中應用梳狀濾波器，並在給出濁音概率估計的情況下進行加權，以改善$\hat{X}_b$中的週期分量。我們使用折積迴圈神經網路來預測增益、音調和濁音概率估計。

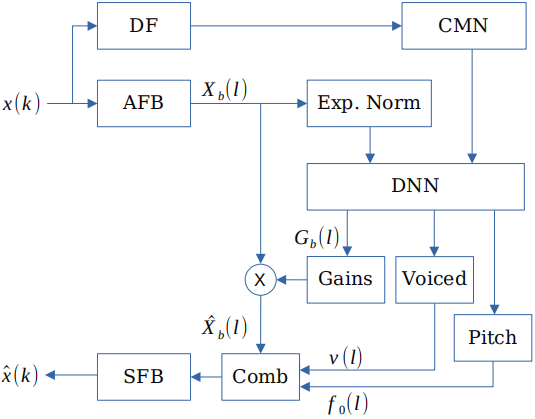
圖1：聯合基音估計和語音增強演演算法概述

2.1  差分函數

　　為了為網路的基音估計任務提供良好的特徵，我們計算了累積平均歸一化差分函數，如[9

$$公式3：d(\tau )=\sum_{j=\tau_{min}}^{\tau_{max}}(x_j-x_{j-\tau})^2$$

其中，$\tau_{max}$和$\tau_{min}$對應60 Hz和500 Hz的lags，lags標誌著我們的演演算法搜尋的最小和最大基音訊率。然後用累積平均值對差分函數進行歸一化

$$公式4：d'(\tau)=\frac{d(\tau)}{\frac{1}{\tau}\sum^\tau_{j=\tau_{min}}d(j)}$$

我們選擇了20 ms的幀大小，並在時間上對齊特徵，如圖3所示。雖然對於我們的應用程式來說，L = 5 ms的最大值是可以接受的，但是我們測試了幾個從0到20 ms的look-aheads。

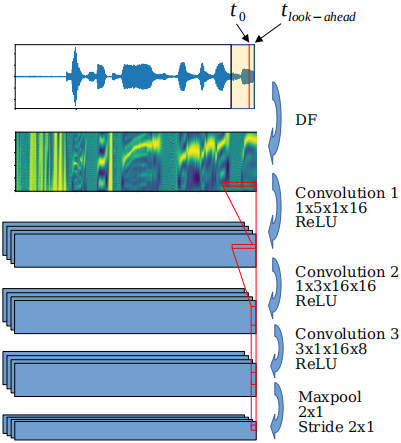
圖3：用於DF特徵的折積編碼器。音訊幀(頂部，以黃色表示)對齊，使其對應於時間位置$t_0$。

這一幀的 look-ahead 是$L=t_{look-ahead}-t_0$。進一步的折積也會在時間上對齊，這樣它們就不會引入額外的延遲。

折積權值(第二行)表示頻率軸和時間軸上的核大小以及輸入輸出通道。

2.2  頻譜歸一化

　　歸一化通常是使深度神經網路(DNN)對不可見輸入資料具有魯棒性的重要組成部分。因此，我們將頻譜轉換為分貝刻度，並在僅確保零均值的情況下執行指數歸一化[13]。我們發現單位方差不能提供任何效能或泛化改進。

$$公式5：X_{b,norm}[l]=X_{b,dB}[l]-\hat{\mu}_b[l]$$

均值估計$\hat{\mu}$由

$$公式6：\hat{\mu}_{b}[l]=\alpha \hat{\mu}_{b}[l-1]+(1-\alpha) X_{b, \mathrm{~dB}}[l]$$

其中$\alpha$對應於3s的歸一化視窗。

3  梳狀濾波器

　　梳狀濾波器通過在輸入訊號中加入延遲訊號，從而產生梳狀頻率響應。最近，梳狀濾波器已被證明可以減少間諧波噪聲來提高整體感知質量[2,3]。通常，梳狀濾波器在時域(TD)計算，定義為

$$公式7：y[k]=\frac{x[k]+x[k-T[k]]}{2}$$

其中$T[k]\in N^+=round(\frac{f_s}{f_0[k]})$是與時間步長$k$處的基音$f_0[k]$相對應的基音週期。在語音應用中，取樣頻率$f_s$足夠高，基音週期的取樣誤差就可忽略不計

　　但是在TD中沒有采用梳狀濾波器，而是完全在頻率(濾波器組)域FD中操作。這有幾個優點。首先，它允許在助聽器中進行預處理，比如波束形成。在這種情況下，只有FD訊號可用，向TD的額外轉換將引入額外的延遲。此外，我們只有經過DNN處理後才有基音估計，其中濾波器組延遲已經被引入。最重要的是，我們可以將梳狀濾波器應用於已經增強的$\hat{X}_b$譜圖，而不是未處理的TD訊號。這有助於決定應該將梳狀濾波器應用到哪一個地方。

　　因為分析視窗只是appox。FD中的梳狀濾波器長度為6ms，其應用方法與TD相同。

$$公式8：Y_{b}[l]=\frac{X_{b}[l]+X_{b}\left[l-T^{\prime}[l]\right] \cdot e^{-j \omega_{k} \tau}}{2}$$

其中$T'[l]=round(T^*[l])=round(sr/f_0[l]/R)$被子取樣因子$R$減小，為了補償濾波器組域中較低的取樣率，我們需要一個相位校正因子$e^{-jw_f\tau}$。它根據頻帶$b$的中心頻率和剩餘延遲( residual delay) $\tau=T^*[l]-T'[l]$來移動FB表示。

　　由於梳式濾波器只能為語音的週期性成分提供好處，因此我們需要對幀l的週期性進行估計。因此，我們估計濁音概率，以便在隨機分量和週期性分量之間定義權重，其中梳狀濾波器應僅應用於週期性幀

$$公式9：\hat{X}_{b}^{\prime}=\hat{X}_{b} \cdot(1-v)+\operatorname{comb}\left(\hat{X}_{b}, T\right) \cdot v$$

$v$可以根據$G_b$估計的區域性訊雜比進行區域性減小。這確保了梳狀濾波器不會衰減純淨的語音。

　　我們還嘗試了更高階的梳狀濾波器，如[3]。然而，由於延遲需求，我們不能使用未來tap，由此產生的群延遲不再可行。

4  DNN模型

　　我們使用了一個帶有兩個編碼器的折積迴圈網路(CRN)，以及單獨的輸出增益G、基音$f_0$和濁音概率$v$。整體結構如圖2所示。我們在頻譜和差分函數(DF)編碼器中都使用時間對齊折積(time aligned convolutions)，不引入圖3所示的任何延遲。與DF編碼器相比，譜圖編碼器不包含最後的折積和maxpool層，以避免過早減少頻率資訊。

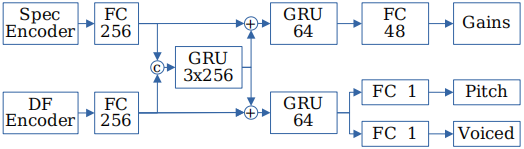
圖2：DNN概述。C表示concatenation操作和+表示加法。嵌入的GRU由3層組成，層下的數位表示輸出隱藏單元

4.1  損失函數

　　我們採用三種不同損失函數的組合損失來進行多目標優化。

$$公式10：L=L_g+L_p+L_{ft}$$

給定 ground truth以及pitch和濁音概率，其中，$L_g$是增益的損失，$L_p$懲罰pitch$\hat{f}_0$，濁音$\hat{v}$估計誤差，而$L_{ft}$是基於濾波後的時域訊號的損失。我們用理想震幅掩模增益作為目標增益[14]，採用[3]的增益損失。這種損失結合了傳統的L2和L4術語，以懲罰過度衰減和退化的語音。

$$公式11：\mathcal{L}_{g}=\sum_{b}\left(g_{b}^{\lambda}-\hat{g}_{b}^{\lambda}\right)^{2}+C_{4} \sum_{b}\left(g_{b}^{\lambda}-\hat{g}_{b}^{\lambda}\right)^{4}$$

其中$\lambda=0.5$是一個常數來匹配感知響度，$C_4$ = 10是一個平衡因子。

　　pitch損失包括pitch上的加權$L_1$損失和語音概率上的$L_2$損失。我們發現，由於預測或ground truth異常值，基音上的L1損失比L2損失更穩健。

$$公式12：\mathcal{L}_{p}=C_{p}\left|c\left(f_{0}\right)-\dot{c}\left(\hat{f}_{0}\right)\right| \cdot v+(v-\hat{v})^{2}$$

其中$C_p$是平衡因子，$\dot{c}(f)=1200log_2(\frac{f}{f_{ref}})$是用cent測量的音調，$f_{ref} = 10Hz$。pitch項以$C_p = 10^{-3}$和target voiced 概率$v$加權，強調目標確定的幀，忽略unvoiced幀。

　　此外，我們利用時域損失來間接改善這兩個任務。這樣做的動機如下。梳狀濾波器只能提高週期性語音部分的感知質量，不能應用於其他幀。另一方面，梳狀濾波器引入了$T /2$的群延遲，使得原始純淨語音不能作為目標。這將迫使voiced概率估計$\hat{v}$為0，梳狀濾波器將根本不適用。因此，我們在給定目標pitch和語音估計(如Eq. 9)的情況下過濾原始純淨的頻譜，然後按照[15]的建議計算TD中的L1損失。通過合成濾波器組將目標估計和語音估計都轉化為時域估計。濾波後的時域損失

$$公式13：L_{ft}=|x'-\hat{x}'|$$

　　結果產生兩種效果。首先，錯誤的基音估計將導致與梳狀濾波器不同的頻率響應，從而導致語音退化，其中有效誤差隨頻率線性增加。在這種情況下，網路可以通過估計更好的基音來改善，或者，如果不可能的話，通過降低$v$至少不降低語音質量。另一個影響是$v$的頻率相關懲罰。對於低基頻，梳狀濾波器的影響減小。諧波更接近，從而產生更好的頻率區域性SNR。因此，該網路的基音估計越低，梳狀濾波器的作用就越小。

4.2  訓練資料

　　我們在大量的語音和噪聲資料上訓練我們的模型，以確保良好的泛化。語音資料集採用EUROM[17]、VCTK[18]和LJ語音[19]。噪聲來自DEMAND[20]、RNNoise資料集[2]以及MUSAN語料庫[21]。後者也包括音樂，我們認為是噪音型別。包括諧波噪聲型別，如發動機噪聲和音樂在訓練中使基音估計更魯棒的現實世界的訊號。此外，我們從Aachen  RIR資料集[22]或通過使用[23]的影象源模型隨機模擬的RIR中增加30%的語音樣本的房間脈衝響應(RIR)。所有這些資料集以70/15/15分割為訓練集、驗證集和測試集。我們將所有語音錄音隨機混合，最多4個噪聲，訊雜比為[-5,0,10,20,100]。

　　基於純淨的語音，用PYIN[6]估計訓練的ground truth pitch。雖然這種pitch估計並不完美，但它為我們的應用提供了足夠精確的目標pitch。有趣的是，與來自純淨語音的目標音調相比，DNN最終在噪聲訓練資料（例如倍頻程誤差）或混響條件下更加穩健。

　　我們使用音調跟蹤資料庫PTDB-TUG[24]來評估我們的方法，該資料庫包含了超過4600個來自看不見的說話人的樣本。PTDB提供的基礎真實pitch是通過應用於喉鏡記錄的RAPT[5]得到的，喉鏡記錄只捕捉到週期性的語音部分。我們使用測試集中相同訊雜比水平的噪聲。RIR增強被禁用以保持幀對齊。

5  實驗和結果

　　我們的模型訓練了20個epoch，batch size為32，使用權重衰減為1e-4的AdamW[25]優化器的學習率為5e-4。圖4為PTDB測試集上的 pitch difference。我們將我們的效能與YIN [9]， PYIN[6]和CREPE[7]進行比較，它們都使用更大的幀大小和look-aheads。由於語音增強多目標訓練和廣泛的噪聲增強，LACOPE在所有訊雜比條件下都具有魯棒性。雖然中值差異比CREPE略差，但從IQR和均值可以看出，異常值的總體數量和強度較低。

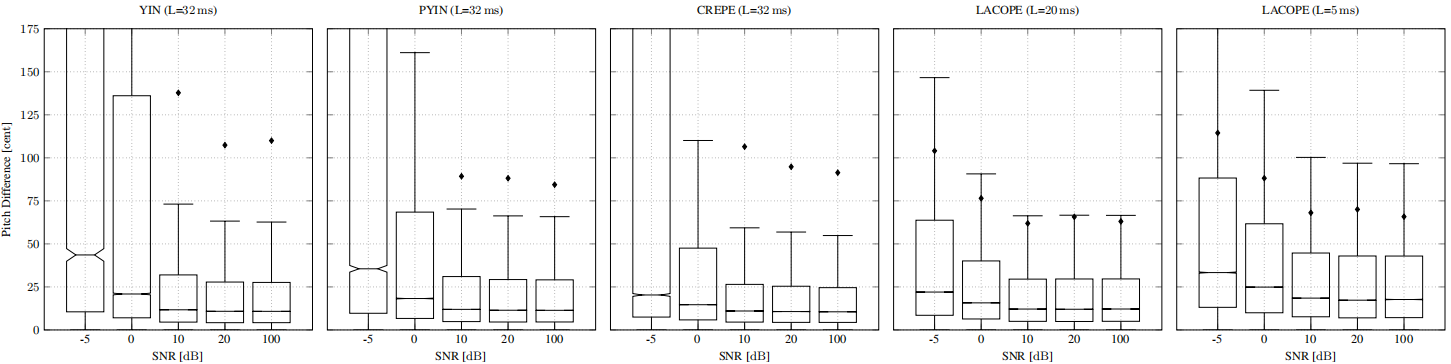
圖4：不同訊雜比條件下PTDB資料的Pitch difference。括號中的L表示Look-ahead，用於衡量異常值的數量和強度。

注意，官方的PYIN Vamp外掛實現在低訊雜比的情況下表現明顯更差。相反，我們將與librosa實現[16]的更好結果進行比較。

　　從圖6可以看出，我們的模型對語音的適應性很好，即使在相同頻率範圍記憶體在諧波噪聲的疊加。請注意，我們的網路傾向於將濁音 period後的幀分類為濁音。然而，這通常不是一個問題，因為如果增益接近於0，梳狀濾波器就沒有效果。CREPE和PYIN經常適應噪聲並將大多數幀歸類為濁音，而PYIN的音調估計通常是octave誤差。

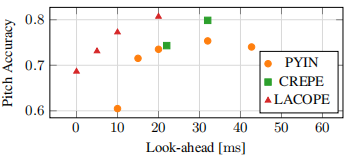
圖5：所有訊雜比下的pitch平均精度我們比較了不同幀大小的PYIN, CREPE以及延遲10毫秒的CREPE，因為幀大小是固定的。

對於PYIN和CREPE，e look-ahead相當於幀大小的一半，幀移不考慮。

　　圖5顯示了以pitch difference低於50 cents的幀的百分比測量的pitch精度。在這裡，look-ahead和pitch準確性之間的權衡變得清晰起來。與相關工作相比，我們可以在較低的預期下取得相當或更好的效能。

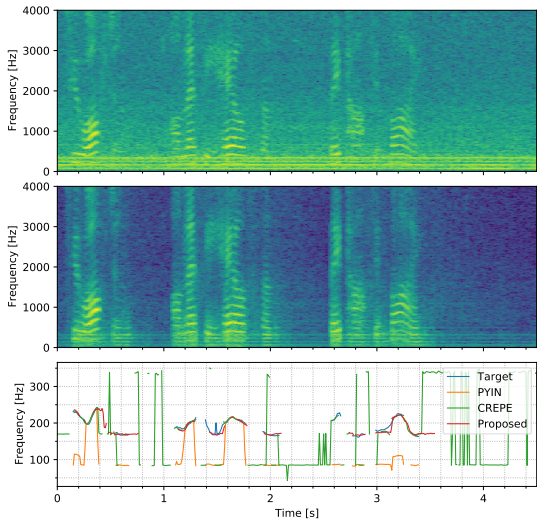
圖6：來自含諧波噪聲測試集的樣本。上面：噪聲譜圖，中間：增強譜圖，下面：音調估計

由於其他的演演算法對各種週期結構都很敏感，所以它們往往只適應噪聲而不適應語音

　　我們不報告語音評估的召回率和精確度等指標。雖然我們的模型是通過PYIN對目標發聲概率估計進行訓練的，但我們認為我們的模型學習了略微不同的表示。最後一項損失的結果並不是語音概率的估計，而是對梳狀濾波器應用到何種程度的估計。因此，輸出是相似的，但不完全相同。

6  結論

　　在本文中，我們提出了LACOPE，一種在低延遲要求下進行基音估計和語音增強的聯合方法。我們表明，與CREPE相比，我們獲得了相當的效能，並且比PYIN更好，特別是在有噪聲的條件下。而我們的模型與約。2.4 M引數和每10 ms段57 MFLOPs對於在嵌入式裝置上執行來說仍然太大了，我們的計算需求包括語音增強比CREPE低很多。在這裡，我們測量到了每10 ms段28.2 BFLOPs，由於大量的折積層，這大約增加了$2*10^6$次操作。

　　為了進一步降低計算需求，我們計劃整合來自[13]的方法，如分層rnn和Bark縮放輸入譜圖和輸出增益。此外，修剪和量化等技術將用於額外的複雜性降低[26]。

7  參考文獻

[1] J. Agnew and J. M. Thornton, Just noticeable and objectionable group delays in digital hearing aids, Journal of the American Academy of Audiology, vol. 11, no. 6, pp. 330 336, 2000.

[2] J.-M. Valin, A hybrid DSP/deep learning approach to real-time full-band speech enhancement, in 2018 IEEE 20th International Workshop on Multimedia Signal Processing (MMSP). IEEE, 2018, pp. 1 5.

[3] J.-M. Valin, U. Isik, N. Phansalkar, R. Giri, K. Helwani, and A. Krishnaswamy, A Perceptually-Motivated Approach for LowComplexity, Real-Time Enhancement of Fullband Speech, in INTERSPEECH 2020, 2020.

[4] J.-M. Valin, G. Maxwell, T. B. Terriberry, and K. Vos, Highquality, low-delay music coding in the opus codec, arXiv preprint arXiv:1602.04845, 2016.

[5] D. Talkin and W. B. Kleijn, A robust algorithm for pitch tracking (RAPT), Speech coding and synthesis, vol. 495, p. 518, 1995.

[6] M. Mauch and S. Dixon, pYIN: A fundamental frequency estimator using probabilistic threshold distributions, in 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2014, pp. 659 663.

[7] J. W. Kim, J. Salamon, P. Li, and J. P. Bello, CREPE: A Convolutional Representation for Pitch Estimation, in 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2018, pp. 161 165.

[8] K. Han and D. Wang, Neural network based pitch tracking in very noisy speech, IEEE/ACM transactions on audio, speech, and language processing, vol. 22, no. 12, pp. 2158 2168, 2014.

[9] A. De Cheveign e and H. Kawahara, YIN, a fundamental frequency estimator for speech and music, The Journal of the Acoustical Society of America, vol. 111, no. 4, pp. 1917 1930, 2002.

[10] X. Zhang, H. Zhang, S. Nie, G. Gao, and W. Liu, A Pairwise Algorithm Using the Deep StackingNetwork for Speech Separation and Pitch Estimation, IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 24, no. 6, pp. 1066 1078, 2016.

[11] E. H ansler and G. Schmidt, Acoustic echo and noise control: a practical approach. John Wiley & Sons, 2005, vol. 40.

[12] M. Aubreville, K. Ehrensperger, A. Maier, T. Rosenkranz, B. Graf, and H. Puder, Deep denoising for hearing aid applications, in 2018 16th International Workshop on Acoustic Signal Enhancement (IWAENC). IEEE, 2018, pp. 361 365.

[13] H. Schr oter, T. Rosenkranz, A. N. Escalante-B. , P. Zobel, and A. Maier, Lightweight Online Noise Reduction on Embedded Devices using Hierarchical Recurrent Neural Networks, in INTERSPEECH 2020, 2020. [Online]. Available: https://arxiv. org/abs/2006.13067

[14] H. Erdogan, J. R. Hershey, S. Watanabe, and J. Le Roux, Phasesensitive and recognition-boosted speech separation using deep recurrent neural networks, in 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2015, pp. 708 712.

[15] U. Isik, R. Giri, N. Phansalkar, J.-M. Valin, K. Helwani, and A. Krishnaswamy, PoCoNet: Better Speech Enhancement with Frequency-Positional Embeddings, Semi-Supervised Conversational Data, and Biased Loss, in INTERSPEECH 2020, 2020.

[16] B. McFee, V. Lostanlen, A. Metsai, M. McVicar, S. Balke, C. Thom e, C. Raffel, F. Zalkow, A. Malek, Dana, K. Lee, O. Nieto, J. Mason, D. Ellis, E. Battenberg, S. Seyfarth, R. Yamamoto, K. Choi, viktorandreevichmorozov, J. Moore, R. Bittner, S. Hidaka, Z. Wei, nullmightybofo, D. Here n u, F.-R. St oter, P. Friesch, A. Weiss, M. Vollrath, and T. Kim, librosa/librosa: 0.8.0, Jul. 2020. [Online]. Available: https: //doi.org/10.5281/zenodo.3955228