淺談樹狀陣列 - tw511教學網

概念：

定義：

樹狀陣列是一種結合了樹的思想，常用來處理字首問題（如字首最大/最小值，字首和）的一種資料結構，區查和單修時間複雜度都為 $\log(n)$。

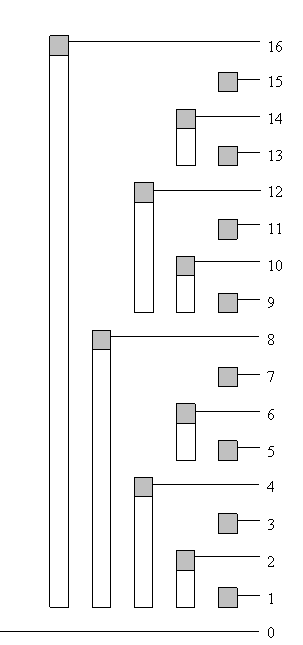
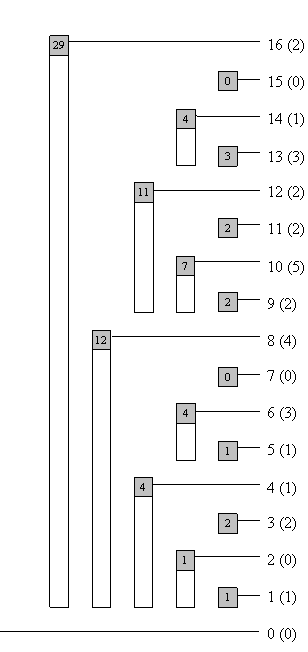
（右圖括號中的值表示原序列中該數的值，未打括號的表示下標）

這一張圖可以很好地展示一維樹狀陣列的結構及其維護資訊的原理。令該樹狀陣列為 $bit$，$c$ 為陣列的字首和，容易發現，$$c[1] = bit[1]$$ $$c[2] = bit[2]$$$$c[3] = bit[2] + bit[3]...$$ $$c[7] = bit[7] + bit[6] + bit[4]$$。

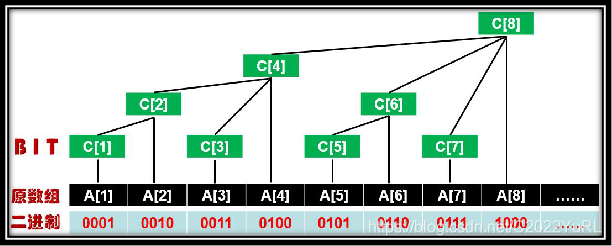
結合圖觀察，通過樹狀陣列求字首和就是將某個區間拆成樹狀陣列裡的若干段的規律就是將該數進行二進位制拆分，每一次取出 $01$ 串中最靠右的 $1$ 表示的數作為樹狀陣列中的下標，然後加起來即可。
例如 $A[5]$，以二進位制表示就是 $A[0101]$ 拆分過後就是 $bit[0100] 和bit[0001]$，分別為 $bit[4]和bit[1]$ 因此 $A[5] = bit[4] + bit[1]$。

lowbit：

那麼如何每次準確地取出 $01$ 串中最靠右的一個 $1$ 呢？這裡需要對當前數取負後再與上當前數即可。
在計算機中，負數用二補數表示，二補數等於正數用二進位制表示後每一位取反後再加一。如 $5$ 用二進位制表示就是 $0101$，那麼 $-5$ 用二進位制表示就是 $0101$ 按位元取反，得到 $1010$，然後加一有 $1011$，這就是 $-5$的二進位制表示法。為了取出最後一位 $1$，還應該將這個數與 $5$ 進行與運算，得到 $0001$，這樣就順利取出了 $01$ 串中的最後一位 $1$。在樹狀陣列的實現中，我們常用這樣一個 $lowbit$ 函數實現這樣的操作：

int lowbit(int i){
	return i & -i;
}

還可以採用互斥或實現 $lowbit$ 此處不展開敘述，讀者自行探索。

一維樹狀陣列：

單修區查：

單修：

仍然結合影象。

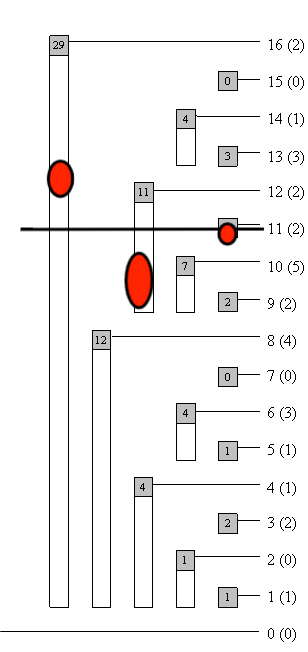
假如我們對原序列中第十一位進行修改，那麼樹狀陣列中，包含原序列第十一位的數的資訊的所有結點都需要改變，這就像從第十一位拉一條水平方向的橫線（如右圖），被這條橫線所切到的所有結點的值都要被改變（紅圓標註）。在這種情況下，樹狀陣列中下標為 $11,12,16$ 的結點都需要被改變。
觀察三數，轉化為二進位制後分別為 $1011,1100,10000$，可以發現，每一個數都相當於前一個數在它最靠右的 $1$ 的位置加上 $1$ 後所得到的數。這裡仍然要用到 $lowbit$
實現如下：

void add(int x,int y){//在下標為x的地方加上y
	for(int i = x; i <= n; i += lowbit(i)){
		bit[i] += y;
	}
}

區查：

按照介紹 $lowbit$ 時所介紹的求字首和的思想進行程式設計：

int query(int x){
	int ans = 0;
	for(int i = x; i > 0; i -= lowbit(i)){
		ans += bit[i];
	}
	return ans;
}

求得字首和，進行區間和查詢也就易如反掌了。

區修單查：

區修：

對於樹狀陣列的區間修改，要運用差分的思想，一個陣列的差分陣列和它的字首和是互逆的。

a[6] = {0, 1, 2, 3, 4, 5};
cf[6] = {0, 1, 1, 1, 1, 1}; //cf[i] = a[i] - a[i - 1] 差分
qzh[6] = {0, 1, 3, 6, 10, 15}; //qzh[i] = qzh[i - 1] + a[i] 字首和

cf_qzh[6] = {0, 1, 2, 3, 4, 5}; //差分陣列的字首和陣列
qzh_cf[6] = {0, 1, 2, 3, 4, 5}; //字首和陣列的差分陣列

容易發現，差分陣列的字首和就是原陣列的數，字首和的差分陣列就是原陣列。
而差分陣列的區間修改是將 $cf[l]+k,cf[r+1]−k$ （設讓 $[l,r]$ 裡的每個數加上 $k$，$cf$ 為原陣列的差分陣列）
對於這道題，我們不再在原陣列上建樹狀陣列了，改在差分陣列上建樹狀陣列。

單查：

每次區間修改，就對 $cf[l]+k,cf[r+1]−k$ ，查詢每個數，即求 $[1,x]$ 的字首和。

void change(int l,int r,int x){//將l到r的數加上x
	add(l,x);
	add(r + 1,-x);
}

$query,add$ 函數不變。

區修區查：

區修：

同上。

區查：

這裡就需要稍微推一下柿子了。設原序列為 $A$。

\[\sum_{l = 1}^r\sum_{j = 1}^ibit[j] \]

這個柿子的結果就是區間和。展開得到：

\[bit[1]+(bit[1]+bit[2])+(bit[1]+bit[2]+bit[3])+⋯+(bit[1]+bit[2]+bit[3]+⋯+bit[p]) \]

\[r∗bit[1]+(r - 1)∗bit[2]+(r−2)∗bit[3]+⋯+2∗bit[r−1]+bit[r] \]

化簡後得：

\[\sum_{i = 1}^rbit[i]∗r−\sum_{i=1}^rbit[i]∗(i−1) \]

因此只需要維護兩個字首和，分別是 $bit[i]和bit[i] * (i - 1)$。

二維樹狀陣列：

單修區查：

其實跟一維的大同小異，這裡就放程式碼了：

void add(int x,int y,int z){
	for(int i = x; i <= n; i += lobit(i)){
		for(int j = y; j <= m; j += lowbit(j)){
			bit[i][j] += z;
		}
	}
}
int query(int x,int y){//左上端點為（1，1），右下端點為（x，y）的矩陣元素之和
	int ans = 0;
	for(int i = x; i > 0; i -= lowbit(i)){
		for(int j = y; j > 0; j -= lowbit(j)){
			ans += bit[i][j];
		}
		return ans;
	}
}

在進行區間矩陣求和時，還要運用到容斥定理，如下圖（找別人薅的

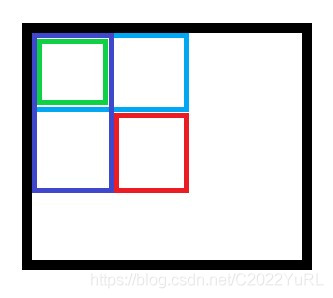
大正方形減去兩個小的長方形，加上小正方形即為紅框區間內的答案。

int tot(int x1,int y1,int x2,int y2){
	int ans = 0;
	ans += add(x2,y2);
	ans -= add(x2,y1 - 1);
	ans -= add(x1 - 1,y2);
	ans += add(x1 - 1,y1 - 1);
	return ans;
}

區修單查：

區修：

一位的區修依賴差分陣列，那麼二維的區修就依賴差分矩陣。
有如下矩陣

想進行區域修改，得到

那麼在差分矩陣裡，就應該是這樣的

程式碼如下：

void change(int x1,int y1,int x2,int y2,int x){
	add(x1,y1,x);
	add(x1,y2 + 1,-x);
	add(x2 + 1,y1,-x);
	add(x2 + 1,y2 + 1,x);
}

單查：

如一維一樣，統計字首和即可。

區修區查：

區修：

同上。

區查：

令 $a$ 為差分矩陣，則有

\[sum = \sum_{i=1}^x\sum_{j=1}^y\sum_{ii=1}^i\sum_{jj=1}^ja[ii][jj] \]

類比一維樹狀陣列，發現 $a[x][y]$ 出現了 $(x - i + 1) * (y - j + 1)$ 次。
所以可以化簡，得到：

\[\sum_{i = 1}^x\sum_{j=1}^ya[i][j]*(x + 1)*(y+1)-\sum_{i=1}^x\sum_{j=1}^ya[i][j]*(x+1)*j-\sum_{i=1}^x\sum_{j=1}^ya[i][j]*(y+1)*i+\sum_{i=1}^x\sum_{j=1}^ya[i][j]*i*j \]

顯而易見，需要維護 $a[i][j] 、a[i][j]∗j、a[i][j]∗i、a[i][j]∗i∗j$

void add(int x, int y, int z) {
    for (int i = x; i <= n; i += lowbit(i))
        for (int j = y; j <= m; j += lowbit(j)) {
        	bit1[i][j] += z;
        	bit2[i][j] += (ll)x * z;
        	bit3[i][j] += (ll)y * z;
        	bit4[i][j] += (ll)x * y * z;
		}
}
void chanhe(int x1,int y1,int x2,int y2,int x){
	Update(x1, y1, x);
	Update(x2 + 1, y2 + 1, x);
	Update(x1, y2 + 1, -x);
    Update(x2 + 1, y1, -x);
}