字尾系列
字尾陣列
字尾陣列的演演算法可以求出所有字尾的排名,並求出 \(height_i=lcp(sa[i],sa[i-1]))\) 這個非常有用的工具
利用倍增演演算法,每一輪求出每個子串 \([i,i+2^k)\) 的排序,那麼下一輪即是把上一輪的結果作為第一關鍵字,\([i+2^k,i+2^{k+1})\) 作為第二關鍵字進行排序,用基排實現
即使用二元組 \((sa_i,sa_{i+2^k})\) 來比較
void get_sa(){
for(int i=1;i<=n;i++)c[x[i]=a[i]]++;
for(int i=1;i<=(m='z');i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;
for(int k=1;k<=n;k<<=1){
int num=0;for(int i=n-k+1;i<=n;i++)y[++num]=i;
for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
for(int i=1;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[x[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i];
memcpy(y,x,sizeof x);x[sa[1]]=num=1;
for(int i=2;i<=n;i++)x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]?num:++num);
if((m=num)==n)break;
}
}
其中
for(int i=n-k+1;i<=n;i++)y[++num]=i;
for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
這兩行的意思是這樣的,\(y\) 表示第二關鍵字排名為 \(i\) 的是那個字尾,即按 \(sa_{i+2^k}\) 排名後的下標
由於從 \(n-k+i\) 開始,長度不夠,所以第二關鍵字為零,自然最小,而剩下的則用 \(sa_{i+2^k}\) 去更新 \(i\) 即可
後面的 \(x\) 陣列表示第 \(i\) 個位置的第一關鍵字排名
直接放一些我也不會證的結論:
利用最後一個結論,可以快速 \(O(n)\) 求出 \(height\) 陣列
void get_height(){
for(int i=1;i<=n;i++)rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1)continue;
if(k)k--;int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&a[i+k]==a[j+k])k++;
height[rk[i]]=k;
}
}
注意如果不使用 \(sa\),設比較兩個字尾大小的複雜度為 \(k\),則樸素的 \(sort\) 下複雜度為 \(knlogn\)
- 樹上字尾排序
考慮問題轉移到樹上其實是多了一個維度,即第一個關鍵字,第二關鍵字,以及它們都相同時會出現第三關鍵字——編號
那麼對三元組 \((sa_i,sa_{fa_{i,j}},i)\) 進行排序即可
程式碼中的 \(rk,y,sa\) 就是分別代表這三個維度的
此時做兩邊雙關鍵字的基排即可
void dosort(int sa[],int x[],int y[],int m){
for(int i=1;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[x[i]]++;
for(int i=1;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i];
}
void get_sa(){
for(int i=1;i<=n;i++)x[i]=i;
dosort(sa,a,x,'z');
rk[sa[1]]=rkk[sa[1]]=num=1;
for(int i=2;i<=n;i++){
rk[sa[i]]=(a[sa[i-1]]==a[sa[i]]?num:++num);
rkk[sa[i]]=i;
}
for(int k=1,j=0;k<=n;k<<=1,j++){
for(int i=1;i<=n;i++)y[i]=rkk[f[i][j]];
dosort(x,y,sa,n);
dosort(sa,rk,x,n);
swap(rk,x);
rk[sa[1]]=rkk[sa[1]]=num=1;
for(int i=2;i<=n;i++){
rk[sa[i]]=(x[sa[i]]==x[sa[i-1]]&&x[f[sa[i]][j]]==x[f[sa[i-1]][j]]?num:++num);
rkk[sa[i]]=i;
}
}
}
字尾自動機
字尾自動機上儲存著一個串的所有字尾,由於所有子串都能通過新增字元變為字尾,所以所有子串也都儲存在字尾自動機中
首先平時構建出的結構由兩部分組成,一個是 \(DAG\) 結構,也就是自動機,這個結構表示出了所有的子串,類似於接受所有子串的 \(AC\) 自動機
一個是 \(parent\) 結構,這個樹形結構維護了 \(endpos\) 集合,有諸多美妙的性質
字尾自動機之所以能壓縮狀態,是因為把所有 \(endpos\) 集合相同的串歸為一個狀態
定義 \(endpos(S)\) 指串 \(S\) 在母串中所有出現時結尾位置的集合,以 \(abaa\) 這個串為例:
\(a:1,3,4\)
\(ab,b:2\)
\(aba,ba:3\)
\(abaa,baa,aa:4\)
對於每一類 \(endpos\) 的字串,都歸入一個節點
\(SAM\) 的 \(fail\) 樹上的父親,是包含這個節點 \(endpos\) 集合的最小集合
有這樣的性質:所有節點兒子的集合沒有交集
對於一個 \(endpos\) 集合,如果給出一個長度 \(len\),那麼就可以唯一確定出一個子串
而對於每個集合長度 \(len\) 都有一定的限制,設為 \(minlen,maxlen\)
有這樣的性質:\(minlen(p)=maxlen(fa(p))+1\)
而 \(SAM\) 本質上是一個 \(DAG\),有向邊代表字元的轉移
有這樣的性質:\(endpos(son[p][w])\subseteq endpos(fa[p])\)
利用以上性質可以證明 \(SAM\) 的點數與邊數規模都為 \(O(n)\)
對於自動機的構建,目前來看似乎需要改動板子的情形不多,大部分情況直接理解性默寫即可
void insert(int w){
int p=last,np=last=++tot;
siz[tot]=1;len[np]=len[p]+1;
for(;p&&!son[p][w];p=fa[p])son[p][w]=np;
if(!p)fa[np]=1;
else{
int q=son[p][w];
if(len[q]==len[p]+1)fa[np]=q;
else{
int nq=++tot;
fa[nq]=fa[q];for(int i=0;i<26;i++)son[nq][i]=son[q][i];
fa[q]=fa[np]=nq;len[nq]=len[p]+1;
for(;p&&son[p][w]==q;p=fa[p])son[p][w]=nq;
}
}
return ;
}
首先 \(np\) 是代表最後一個字尾的節點,整個過程一個主要目的是為了給其找父親
順著 \(endpos\) 是最後一個點的鏈往上爬直到有 \(w\) 這個兒子
如果沒有,直接認 \(1\) 為兒子,結束
至於另外的情況如果不滿足長度條件會產生的影響,目前還沒有看懂,總之應該把 \(q\) 分裂成兩個節點
\(update:\)
經過一番手模以後有了一些新的理解
對於分裂那塊,舉一個簡單的例子,比如插入 abb
前兩個字母的時候長這樣
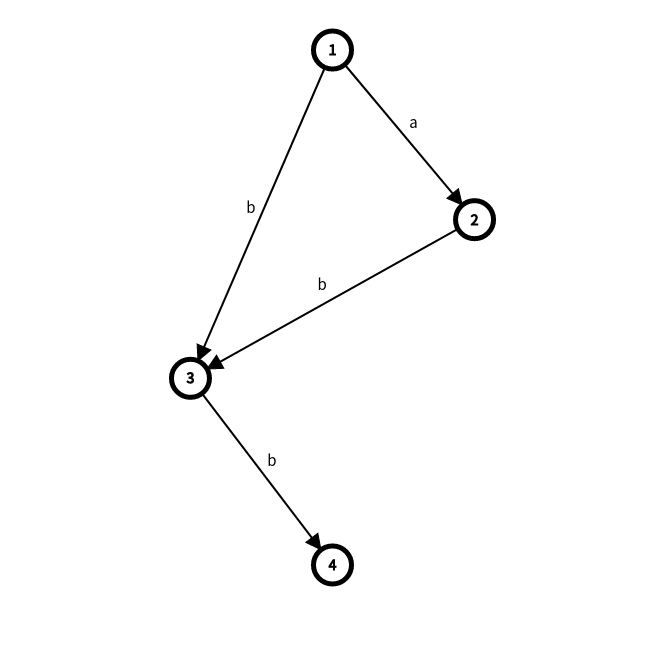
再插入一個 \(b\),可以發現原來 \([3,3]\) 這個子串並不能表示出來,因為雖然 \(3\) 號點可以表示 \(b\),但是 \(3\) 的endpos是 \(2\)
因此需要把 \(3\) 拆成兩個點,變成這樣
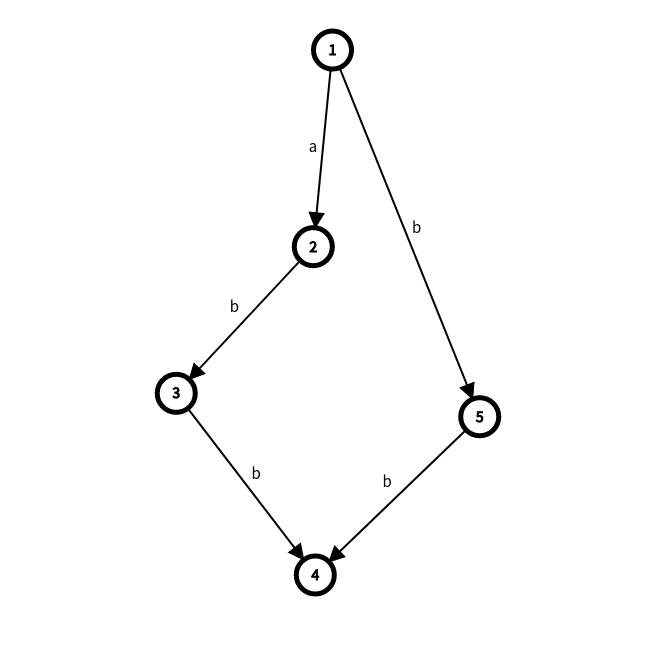
其中 \(5\) 號點的 \(endpos\) 是 \(2,3\),正好成為 \(3,4\) 的父親
一個小 \(trick\) 是如果不需要建出真實的樹,可以按照 \(len\) 排序的結果倒序遍歷即為父子關係的倒序關係
- 線段樹合併
如果想要得知某個節點的 \(endpos\) 集合,那麼可以在 \(SAM\) 上線段樹合併
注意要寫成不銷燬節點的版本,即對於每一個兩個樹都有的節點都要新建一個節點
這樣一來就可以對某一個子串的資訊進行利用了,比如要知道 \([l,r]\) 的自動機結構
那麼假設當前匹配長度為 \(len\),那麼 \(u->v\) 時選取 \(v\) 的不超過 \(r\) 的最大 \(endpos\),\(check\) 其是否超過了左端點,超過了就需要跳 \(fail\) 調整
- 廣義 \(SAM\)
相當於是每次插入字元時插入到上一個字元的後面
假如直接每個串分別構建會使得不同串的相同子串分叉成兩個兒子從而丟失資訊,用兩種解決方法:
每次加入時特判是否已經存在當前兒子:
if(son[last][w]){
int q=son[last][w];
if(len[q]==len[last]+1)last=q;
else{
int nq=++tot;fa[nq]=fa[q];memcpy(son[nq],son[q],sizeof son[q]);
fa[q]=nq;len[nq]=len[last]+1;
for(;son[last][w]==q;last=fa[last])son[last][w]=nq;
last=nq;
}
return ;
}
也可以對所有串建出 \(trie\) 樹,然後 \(bfs\) 建立,因為這樣一來按長度順序插入就不會有問題了
void bfs() {
queue<int> q;q.push(0);pos[0] = 1;
while (!q.empty()) {
int p = q.front();q.pop();
for (int i = 0; i < 26; i++)
if (trie[p][i]) {
pos[trie[p][i]] = insert(pos[p], i);
q.push(trie[p][i]);
}
}
}
廣義 \(SAM\) 的核心是統計子樹內的顏色資訊,如果想要直到具體的編號可以採用類似的方法線段樹合併得到
字尾樹
字尾樹是把所有字尾建出 \(trie\) 樹並把二度點縮成一條邊的結構,也可以理解為字尾 \(trie\) 的虛樹
定義等價類為從根出發沿著 \(trie\) 樹走出的某個串,其在原串的起始位置集合,記為 \(startpos\)
那麼有性質 \(startpos\) 為包含關係,也就是說字尾樹非常自然地用樹形結構刻畫出了 \(startpos\) 合併的過程
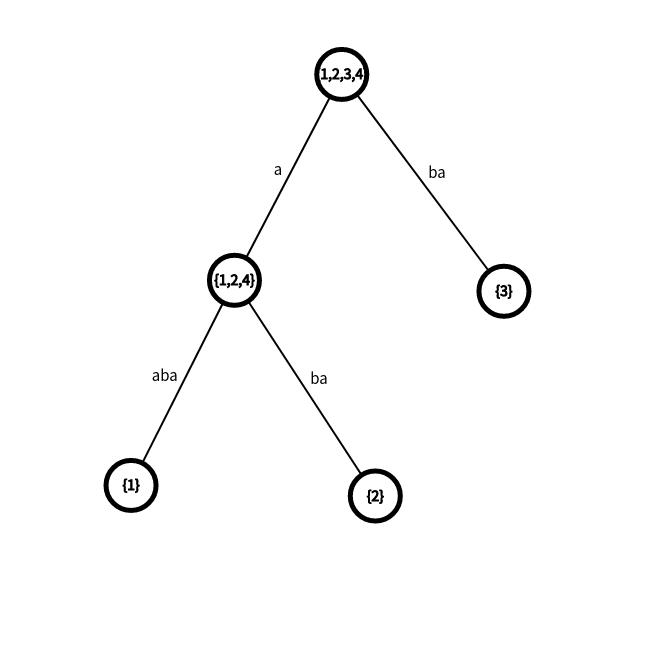
字尾樹的大小不超過 \(2n\)
有結論字尾樹是反串的 \(parent\) 樹
那麼樹上的邊代表的字串可以由構建 \(SAM\) 時保留的一個 \(endpos\) 和 \(len\) 很容易求出來
- 字尾陣列與字尾樹:字尾樹上按照字典序遍歷兒子得到的 \(dfs\) 序即為字尾陣列,子樹結構對應字尾陣列的區間結構
- 兩個字尾的 \(lcp\) 為兩個樹上節點的 \(lca\),而這種 \(lca\) 的合併性與字尾陣列 \(height\) 陣列的合併對應
經典問題
本質不同的子串數
自動機結構:本質不同的子串即為從根出發沿 \(DAG\) 行走的路徑條數,用拓撲排序+\(dp\) 即可解決
樹形結構:為每個節點可以表示出的子串範圍,即 \(mxlen-mnlen+1\)(可以發現這種方法可以支援動態加入)
字尾樹:字尾樹上從根到每一個點(包括被壓縮的)的路徑都是本質不同的,那麼統計所有樹邊的長度和即可
字尾陣列:答案為總個數減去重複子串個數,而每一對重複子串都可以唯一地表示成兩個字尾的 \(lcp\),因此答案即為 \(ans-\sum_{i=2}^n height_i\)
P2408 不同子串個數,P4070 [SDOI2016]生成魔咒
子串定位:將給定子串定位在 \(SAM\) 上對應的節點
\(SAM\):首先找到 \(r\) 這個節點插入後的節點,這個節點表示的是 \(r\) 這個字首,那麼其 \(parent\) 樹上的祖先即為這個字首的所有字尾,倍增即可,\(check\) 長度是否達到子串長度
字尾樹:類似地從這個字尾的關鍵點往上倍增
子串出現次數
樹形結構:為子串對應節點的 \(endpos\) 集合大小
字尾陣列:在對應的 \(sa\) 陣列上往兩邊二分,找到最大的一個區間即為
字尾樹:查詢子串對應子樹的關鍵點大小即可
最長公共子串
其核心是快速對 \(T\) 的每一個字首快速求出 \(LCS\)
\(SAM\):首先需要確定 \(T\) 的每一個字首的位置,那麼直接類似於 \(AC\) 自動機往下匹配,找不到兒子的時候直接跳 \(fail\) 即可(因為跳 \(fail\) 相當於跳這個字首的字尾,這是貪心的思想,相當於是優先從 \(T\) 的前面彈出失配的字元)
字尾陣列:類似地轉化成求每一個字尾的 \(LCP\),那麼把串接在後面跑完 \(sa\) 後尋找前後第一個異色點即可,這樣可以保證 \(lcp\) 最大
字尾樹:接在一起構建字尾樹,答案即為最深的子樹內同時有兩種關鍵點的點
對於多個串的情況,字尾陣列與字尾樹都類似,\(SAM\) 可以把其餘串都往第一個上跑,對每個節點取 \(min\) 再求 \(max\) 即可,也可以採用廣義 \(SAM\),與字尾樹同理
最長不相交子串
\(SAM\):維護出每個 \(endpos\) 的 \(mnlen\) 和 \(mxlen\) 即可
字尾陣列:首先二分答案,然後對分成的塊中統計位置的最大最小值
自動機結構:一個子串相當於從起點出發的一條路徑,考慮 \(dp\) 出走當前節點的所有出邊將會產生有多少個子串,把點權設為 \(1\) 或出現次數跑反圖的拓撲 \(dp\) 即可
字尾樹:把一個節點的所有兒子排序可以按照字典序遍歷到所有子串,統計每種點權意義下的子樹大小即可
考慮還是採用經典的分段法,那麼在每一段中統計最大、次大、最小、次小值即可
如果按照正序求解是一個分裂問題,那麼採用類似並查集的時光倒流套路倒序求解,變成了每次合併區間就很好維護了
程式碼
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=3e5+5;
const int inf=0x3f3f3f3f3f3f3f3f;
int n,m,c[maxn],sa[maxn],x[maxn],y[maxn],rk[maxn],height[maxn],fa[maxn],siz[maxn],sum,val=-inf,a[maxn],mx[maxn],cmx[maxn],mn[maxn],cmn[maxn];
vector<int>ex[maxn];
pair<int,int>ans[maxn];
char s[maxn];
int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-48;
ch=getchar();
}
return x*f;
}
void get_sa(){
for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
for(int i=2;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i;i--)sa[c[x[i]]--]=i;
for(int k=1;k<=n;k<<=1){
int num=0;
for(int i=n-k+1;i<=n;i++)y[++num]=i;
for(int i=1;i<=n;i++){
if(sa[i]>k)y[++num]=sa[i]-k;
}
for(int i=1;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[x[i]]++;
for(int i=2;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=1;
num=1;
for(int i=2;i<=n;i++){
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
}
if(num==n)break;
m=num;
}
return ;
}
void get_height(){
for(int i=1;i<=n;i++)rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1)continue;
if(k)k--;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k])k++;
height[rk[i]]=k;
}
return ;
}
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
int calc_val(int x){
return x*(x-1)/2;
}
void calc(int p){
for(int i=0;i<ex[p].size();i++){
int x=ex[p][i];
int xx=find(x-1);
int yy=find(x);
sum+=calc_val(siz[xx]+siz[yy])-calc_val(siz[xx])-calc_val(siz[yy]);
fa[xx]=yy;
siz[yy]+=siz[xx];
int d[6]={-inf,mx[xx],cmx[xx],mx[yy],cmx[yy]};
sort(d+1,d+5);
// for(int i=1;i<=4;i++)cout<<d[i]<<" ";
// cout<<endl;
mx[yy]=d[4];
cmx[yy]=d[3];
int b[6]={-inf,mn[xx],cmn[xx],mn[yy],cmn[yy]};
sort(b+1,b+5);
// for(int i=1;i<=4;i++)cout<<b[i]<<" ";
// cout<<endl;
mn[yy]=b[1];
cmn[yy]=b[2];
val=max(val,max(mx[yy]*cmx[yy],mn[yy]*cmn[yy]));
}
ans[p]=make_pair(sum,val);
if(val==-inf)ans[p].second=0;
return ;
}
signed main(){
n=read();
scanf("%s",s+1);
for(int i=1;i<=n;i++)a[i]=read();
m=122;
get_sa();
get_height();
for(int i=2;i<=n;i++)ex[height[i]].push_back(i);
for(int i=1;i<=n;i++){
fa[i]=i;
siz[i]=1;
mx[i]=mn[i]=a[sa[i]];
cmx[i]=-inf;
cmn[i]=inf;
}
for(int i=n-1;i>=0;i--)calc(i);
for(int i=0;i<n;i++)printf("%lld %lld\n",ans[i].first,ans[i].second);
return 0;
}
字尾陣列:首先轉化一下先算出自己內部的 \(lcp\) 最後減去,就不用關心從哪個串來的了。那麼就是要算出所有區間的 \(height\) 的 \(min\) 之和,可以用單調棧方便解決
字尾樹:這題的公式給的非常奇怪,考慮其實際意義,如果放到字尾樹上,那麼代表著兩個字尾節點的路徑長度,統計這個東西就好了,即為 \(w* siz_u(n-siz_u)\)
程式碼
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+50;
int n,m,c[maxn],x[maxn],y[maxn],sa[maxn],rk[maxn],height[maxn],tp,sta[maxn],l[maxn],r[maxn];
long long ans;
char s[maxn];
void get_sa(){
for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
for(int i=2;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;
for(int k=1;k<=n;k<<=1){
int num=0;
for(int i=n-k+1;i<=n;i++)y[++num]=i;
for(int i=1;i<=n;i++){
if(sa[i]>k)y[++num]=sa[i]-k;
}
for(int i=1;i<=m;i++)c[i]=0;
for(int i=1;i<=n;i++)c[x[i]]++;
for(int i=2;i<=m;i++)c[i]+=c[i-1];
for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
num=1;
x[sa[1]]=1;
for(int i=2;i<=n;i++){
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
}
if(num==n)break;
m=num;
}
return ;
}
void get_height(){
for(int i=1;i<=n;i++)rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1)continue;
if(k)k--;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k])k++;
height[rk[i]]=k;
}
return ;
}
int main(){
// freopen("2.out","w",stdout);
scanf("%s",s+1);
n=strlen(s+1);
ans=(1ll*n*n*n-n)/2;
// cout<<ans<<endl;
m=122;
get_sa();
get_height();
sta[0]=1;
for(int i=2;i<=n;i++){
// cout<<height[i]<<" ";
while(tp&&height[sta[tp]]>=height[i])r[sta[tp]]=i-1,tp--;
sta[++tp]=i;
l[i]=sta[tp-1]+1;
}
while(tp)r[sta[tp]]=n,tp--;
for(int i=2;i<=n;i++){
// cout<<l[i]<<" "<<r[i]<<endl;
ans-=2ll*height[i]*(r[i]-i+1)*(i-l[i]+1);
}
cout<<ans;
return 0;
}
仍然是匹配的模式,考慮迴圈同構的處理方法
相當於長度擴充套件一倍,每次要求長度小於 \(len\)
由於本質不同的只算一次,那麼字尾自動機上的每個節點打時間戳去重即可
程式碼
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+5;
int n,m,to[maxn],len[maxn],id[maxn],son[maxn][26],fa[maxn],ans,siz[maxn],last=1,tot=1,vis[maxn];
char a[maxn];
void insert(int w){
int p=last,np=last=++tot;
len[np]=len[p]+1;siz[np]=1;
for(;p&&!son[p][w];p=fa[p])son[p][w]=np;
if(!p)fa[np]=1;
else{
int q=son[p][w];
if(len[q]==len[p]+1)fa[np]=q;
else{
int nq=++tot;fa[nq]=fa[q];
memcpy(son[nq],son[q],sizeof son[nq]);
len[nq]=len[p]+1;fa[q]=fa[np]=nq;
for(;p&&son[p][w]==q;p=fa[p])son[p][w]=nq;
}
}
return ;
}
int main(){
scanf("%s",a+1);n=strlen(a+1);
for(int i=1;i<=n;i++)insert(a[i]-'a');
// for(int i=1;i<=tot;i++)cout<<siz[i]<<" "<<fa[i]<<endl;;
for(int i=1;i<=tot;i++)to[len[i]]++;
for(int i=1;i<=tot;i++)to[i]+=to[i-1];
for(int i=1;i<=tot;i++)id[to[len[i]]--]=i;
for(int i=tot;i>=1;i--)siz[fa[id[i]]]+=siz[id[i]];
// for(int i=1;i<=tot;i++)cout<<siz[i]<<" ";
cin>>m;
for(int t=1;t<=m;t++){
scanf("%s",a+1);n=strlen(a+1);ans=0;
for(int i=1,p=1,nowlen=0;i<n*2;i++){
int w=a[(i-1)%n+1]-'a';
if(!son[p][w]){for(;p&&!son[p][w];p=fa[p]);nowlen=len[p];}
if(!p){p=1;continue;}
p=son[p][w];nowlen++;
while(nowlen>n){
nowlen--;
if(nowlen<=len[fa[p]])p=fa[p];
}
if(nowlen>=n&&vis[p]!=t)ans+=siz[p],vis[p]=t;//,cout<<"hhh "<<nowlen<<" "<<p<<endl;
//cout<<p<<endl;
}
printf("%d\n",ans);
}
return 0;
}
這次多了區間的限制
考慮還是跑出長度 \(f[i]\),那麼對於區間 \([l,r]\) 相當於是查詢 \(max\{min(f[i],i-l+1)\}\)
發現內層多了個 \(min\) 不好處理,由於 \(f[i]\) 每次加一具有單調性,那麼可以先二分答案,使得每一個都不受限制,然後用 \(ST\) 表查詢區間最大值
程式碼
#include<bits/stdc++.h>
using namespace std;
const int maxn=4e5+5;
int n,m,fa[maxn],len[maxn],son[maxn][26],f[maxn][26],lg[maxn*10],po[maxn],l,r,last=1,tot=1,t;
char a[maxn],b[maxn];
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void insert(int w){
int p=last,np=last=++tot;
len[np]=len[p]+1;
for(;p&&!son[p][w];p=fa[p])son[p][w]=np;
if(!p)fa[np]=1;
else{
int q=son[p][w];
if(len[q]==len[p]+1)fa[np]=q;
else{
int nq=++tot;fa[nq]=fa[q];
memcpy(son[nq],son[q],sizeof son[nq]);
len[nq]=len[p]+1;fa[q]=fa[np]=nq;
for(;p&&son[p][w]==q;p=fa[p])son[p][w]=nq;
}
}
return ;
}
int ask(int l,int r){
if(l>r)return 0;
int le=lg[r-l+1];
return max(f[l][le],f[r-po[le]+1][le]);
}
void pre(){
t=20;po[0]=1;//t+=2;
for(int i=1;i<=t;i++){
po[i]=po[i-1]*2;
for(int j=po[i-1];j<po[i];j++)lg[j]=i-1;
}
for(int j=1;j<=t;j++){
for(int i=1;i<=n;i++){
f[i][j]=max(f[i][j-1],f[i+po[j-1]][j-1]);
}
}
return ;
}
int main(){
// freopen("P6640_6.in","r",stdin);
// freopen("my.out","w",stdout);
scanf("%s%s",a+1,b+1);n=strlen(a+1),m=strlen(b+1);
for(int i=1;i<=m;i++)insert(b[i]-'a');
for(int i=1,p=1,nowlen=0;i<=n;i++){
int w=a[i]-'a';
if(!son[p][w]){
for(;p!=1&&!son[p][w];p=fa[p]);
nowlen=len[p];
}
if(son[p][w])p=son[p][w],nowlen++;
f[i][0]=nowlen;
// cout<<f[i][0]<<endl;
}
// return 0;
pre();t=read();int cnt=0;
// cout<<"hhhh"<<endl;
while(t--){
cnt++;l=read(),r=read();
int lx=l,rx=r+1,pos=r+1;
while(lx<rx){
int mid=lx+rx>>1;
if(mid-f[mid][0]+1>=l)rx=mid;
else lx=mid+1;
}
// cout<<"hhh "<<lx<<endl;
// if(lx+1-f[lx+1][0]+1>=l)lx++;
// cout<<pos<<" "<<r<<endl;
// if(cnt==565)lx++,cout<<lx<<endl,
printf("%d\n",max(ask(lx,r),lx-l));
}
return 0;
}
考慮沒有區間限制的暴力做法:對 \(S\) 的 \(SAM\) 跑 \(T\) 進行匹配,跑到第一個沒有匹配項的地方找到比 \(T\) 大的轉移,如果都能匹配上,那麼往回退,直到有一個滿足條件的
現在有了區間的限制,如果能判斷字尾自動機上的這個節點的 \(endpos\) 集合中有沒有當前區間內的點就可以正常做了,那麼直接在 \(parent\) 樹上線段樹合併維護 \(endpos\) 集合即可
程式碼
#include<bits/stdc++.h>
using namespace std;
const int maxn=4e5+5;
const int maxm=8e5+5;
int n,m,endpos[maxn],len[maxn],fa[maxn],son[maxn][26],hd[maxn],cnt,rt[maxn],l,r,ans,sta[maxn],last=1,tot=1,tp,nn;
char a[maxn];
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void insert(int w,int id){
int p=last,np=last=++tot;
endpos[np]=id;len[np]=len[p]+1;
for(;p&&!son[p][w];p=fa[p])son[p][w]=np;
if(!p)fa[np]=1;
else{
int q=son[p][w];
if(len[q]==len[p]+1)fa[np]=q;
else{
int nq=++tot;fa[nq]=fa[q];
memcpy(son[nq],son[q],sizeof son[nq]);
len[nq]=len[p]+1;fa[q]=fa[np]=nq;
for(;p&&son[p][w]==q;p=fa[p])son[p][w]=nq;
}
}
return ;
}
struct Edge{
int nxt,to;
}edge[maxm];
void add(int u,int v){
// cout<<"edge: "<<u<<" "<<v<<endl;
edge[++cnt].nxt=hd[u];
edge[cnt].to=v;
hd[u]=cnt;
return ;
}
struct Seg{
int l,r,son[2];
}t[maxn*40];
int change(int p,int l,int r,int w){
if(!p)p=++tot;t[p].l=l,t[p].r=r;
// cout<<p<<" "<<l<<" "<<r<<" "<<w<<endl;
if(l==r)return p;
int mid=l+r>>1;
if(w<=mid)t[p].son[0]=change(t[p].son[0],l,mid,w);
else t[p].son[1]=change(t[p].son[1],mid+1,r,w);
return p;
}
int merge(int p,int q){
if(!p||!q)return p+q;
int np=++tot;t[np].l=t[p].l,t[np].r=t[p].r;
t[np].son[0]=merge(t[p].son[0],t[q].son[0]);
t[np].son[1]=merge(t[p].son[1],t[q].son[1]);
return np;
}
bool ask(int p,int l,int r,int ll,int rr){
// cout<<p<<" "<<l<<" "<<r<<" "<<ll<<" "<<rr<<endl;
if(!p)return false;
if(t[p].l>=l&&t[p].r<=r)return true;
int mid=ll+rr>>1;
if(l<=mid&&ask(t[p].son[0],l,r,ll,mid))return true;
if(r>mid&&ask(t[p].son[1],l,r,mid+1,rr))return true;
return false;
}
void dfs(int u){
if(endpos[u])rt[u]=change(rt[u],1,n,endpos[u]);//,cout<<u<<" "<<endpos[u]<<endl;
for(int i=hd[u];i;i=edge[i].nxt){
int v=edge[i].to;
dfs(v);rt[u]=merge(rt[u],rt[v]);
}
return ;
}
bool check(int p,int l,int r,int len){
// cout<<p<<" "<<l<<" "<<r<<" "<<len<<endl;
if(l+len>r)return false;
return ask(rt[p],l+len,r,1,nn);
}
int main(){
scanf("%s",a+1);nn=n=strlen(a+1);m=read();
for(int i=1;i<=n;i++)insert(a[i]-'a',i);
for(int i=2;i<=tot;i++)add(fa[i],i);tot=0;dfs(1);
// cout<<ask(rt[4],1,2,1,n)<<endl;return 0;
while(m--){
l=read(),r=read();scanf("%s",a+1);
int p=1;sta[tp=1]=1;n=strlen(a+1);ans=27;
for(int i=1;i<=n;i++){
int w=a[i]-'a';
int to=son[p][w];
if(to&&check(to,l,r,i-2))sta[++tp]=p=to;
else break;
}
a[n+1]='a'-1;
while(ans==27&&tp>=0){
p=sta[tp];
for(int j=a[tp]-'a'+1;j<26;j++){
if(son[p][j]&&check(son[p][j],l,r,tp-1)){
ans=j;break;
}
}
tp--;
}
// cout<<ans<<endl;
if(ans==27)puts("-1");
else{
for(int i=1;i<=tp;i++)putchar(a[i]);
putchar(ans+'a');puts("");
}
}
return 0;
}
首先建出字尾樹,那麼可以按照字元排序兒子,之後得到的 \(dfs\) 序即為字典序排序後的結果
由於優先考慮長度,那麼求出每種長度的個數以後可以確定答案的長度了
那麼用一棵線段樹維護當前 \(dfs\) 序上的個數,線段樹二分就可以了
程式碼
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define fi first
#define se second
#define mp make_pair
const int maxn=2e6+5;
typedef pair<int,int>pi;
int n,q,last=1,tot=1,fa[maxn],siz[maxn],len[maxn],rig[maxn],re[maxn],mlen[maxn],cf[maxn],dfn[maxn],rem[maxn],num;
map<int,int>son[maxn];
vector<pi>has[maxn],que[maxn],op[maxn];
ll k,sum[maxn];
pi ans[maxn];
char a[maxn];
ll read(){
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void insert(int w,int id){
int p=last,np=last=++tot;
len[np]=len[p]+1;siz[np]=1;rig[np]=id;
for(;p&&!son[p][w];p=fa[p])son[p][w]=np;
if(!p)fa[np]=1;
else{
int q=son[p][w];
if(len[q]==len[p]+1)fa[np]=q;
else{
int nq=++tot;fa[nq]=fa[q];rig[nq]=id;
son[nq]=son[q];
// memcpy(son[nq],son[q],sizeof son[q]);
len[nq]=len[p]+1;fa[q]=fa[np]=nq;
for(;p&&son[p][w]==q;p=fa[p])son[p][w]=nq;
}
}
return ;
}
void add(int u,int v,int w){has[u].pb({w,v});has[u].shrink_to_fit();}
void dfs(int u){
sort(has[u].begin(),has[u].end());
for(auto v:has[u]){
dfn[v.se]=++num;rem[num]=v.se;
dfs(v.se);rig[u]=max(rig[u],rig[v.se]);
op[mlen[v.se]].pb({v.se,1});
op[len[v.se]+1].pb({v.se,-1});
}
return ;
}
void build(){
for(int i=2;i<=tot;i++){
cf[mlen[i]=len[fa[i]]+1]++;
cf[len[i]+1]--;
add(fa[i],i,a[rig[i]-mlen[i]+1]);
}
dfs(1);for(int i=1;i<=n;i++)cf[i]+=cf[i-1],sum[i]=sum[i-1]+cf[i];
// for(int i=1;i<=n;i++)cout<<sum[i]<<" ";puts("");
return ;
}
struct Seg{
int l,r,sum;
}t[maxn*4];
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r)return re[l]=p,void();
int mid=l+r>>1;build(p<<1,l,mid),build(p<<1|1,mid+1,r);
}
void change(int p,int w){
p=re[p];t[p].sum+=w;
while(p>>1)p>>=1,t[p].sum+=w;
return ;
}
int ask(int p,int w){
if(t[p].l==t[p].r)return t[p].l;
if(t[p<<1].sum<w)return ask(p<<1|1,w-t[p<<1].sum);
return ask(p<<1,w);
}
void solve(){
build(1,1,tot);
for(int i=1;i<=n;i++){
for(auto x:op[i])change(dfn[x.fi],x.se);
for(auto x:que[i]){
int pos=ask(1,x.fi);pos=rem[pos];
ans[x.se]=mp(n-rig[pos]+1,n-rig[pos]+i);
}
}
return ;
}
signed main(){
scanf("%s",a+1);n=strlen(a+1);reverse(a+1,a+n+1);
for(int i=1;i<=n;i++)insert(a[i]-'a',i);
build();q=read();
for(int i=1;i<=q;i++){
k=read();
if(k>sum[n]){ans[i]=mp(-1,-1);continue;}
int pos=lower_bound(sum+1,sum+n+1,k)-sum;
que[pos].pb({k-sum[pos-1],i});
}
solve();for(int i=1;i<=q;i++)printf("%d %d\n",ans[i].fi,ans[i].se);
return 0;
}
字串
題意:定義相似為之多一個位置不同,求所有長度為 \(m\) 的子串的相似串個數
考慮兩個 \(m\) 子串 \(i,j\) 如果相似需要滿足 \(lcp(i,j)+lcs(i+m-1,j+m-1)\ge m-1\)
考慮建出兩個字尾樹,那麼就是要統計有多少點對滿足兩棵樹上的 \(lca\) 深度之和 \(\ge m-1\)
涉及到點對統計問題,考慮使用 \(dsu\) \(on\) \(tree\) 解決
在字首樹上找到一個字首,設當前列舉的 \(lca\) 的深度為 \(d\),那麼在字尾樹上找到一個最淺的祖先,滿足 \(dep\ge m-1-d\) 即可
這個需要用兩個樹狀陣列實現,注意是兩個,因為需要得知具體的個數,所以一個區間查詢,一個單點查詢
單點查詢的比較難做,可以把一個數計入貢獻的時候減去目前樹狀陣列的值,去除貢獻的時候再加上即可
程式碼
#include<bits/stdc++.h>
using namespace std;
#define pb push_back
const int maxn=2e5+5;
int n,m,t,ans[maxn],sta[maxn],tp;
char a[maxn];
vector<int>sta1;
struct BIT{
int c[maxn];
void add(int x,int w){for(;x<=2*n;x+=x&-x)c[x]+=w;}
int ask(int x){int res=0;for(;x;x-=x&-x)res+=c[x];return res;}
void add(int l,int r,int w){add(l,w),add(r+1,-w);}
int ask(int l,int r){return ask(r)-ask(l-1);}
}tr[2];
struct SAM{
int len[maxn],son[maxn][26],fa[maxn],last=1,tot=1,re[maxn],pos[maxn],dfn[maxn],num,siz[maxn],son1[maxn],f[maxn][20],ed[maxn];
vector<int>has[maxn];
void insert(int w,int po){
int p=last,np=last=++tot;len[np]=len[p]+1;pos[re[np]=po]=np;
for(;p&&!son[p][w];p=fa[p])son[p][w]=np;
if(!p)return fa[np]=1,void();
int q=son[p][w];
if(len[q]==len[p]+1)fa[np]=q;
else{
int nq=++tot;len[nq]=len[p]+1;
memcpy(son[nq],son[q],sizeof son[nq]);
fa[nq]=fa[q];fa[q]=fa[np]=nq;
for(;p&&son[p][w]==q;p=fa[p])son[p][w]=nq;
}
}
void dfs(int u){
dfn[u]=++num;siz[u]=1;
for(int v:has[u]){
f[v][0]=u;
for(int i=1;i<=t;i++)f[v][i]=f[f[v][i-1]][i-1];
dfs(v);siz[u]+=siz[v];
if(siz[v]>siz[son1[u]])son1[u]=v;
}
ed[u]=num;
}
int find(int x,int w){for(int i=t;i>=0;i--)if(f[x][i]&&len[f[x][i]]>=w)x=f[x][i];return x;}
void build(bool op){
if(!op){
for(int i=1;i<=n;i++)insert(a[i]-'a',i);
for(int i=1;i<m;i++)re[pos[i]]=0;
}
else for(int i=n;i>=1;i--)insert(a[i]-'a',i);
for(int i=2;i<=tot;i++)has[fa[i]].pb(i);dfs(1);
}
}pre,suf;
void insert(int u){
tr[1].add(suf.dfn[suf.pos[pre.re[u]-m+1]],1);sta[++tp]=u;
ans[pre.re[u]-m+1]-=tr[0].ask(suf.dfn[suf.pos[pre.re[u]-m+1]]);
}
void insert1(int u,int pa){
int to=suf.find(suf.pos[pre.re[u]-m+1],m-1-pre.len[pa]);
ans[pre.re[u]-m+1]+=tr[1].ask(suf.dfn[to],suf.ed[to]);
tr[0].add(suf.dfn[to],suf.ed[to],1);
}
void clear(){
while(tp){
int u=sta[tp];
if(pre.re[u])ans[pre.re[u]-m+1]+=tr[0].ask(suf.dfn[suf.pos[pre.re[u]-m+1]]);
tr[1].add(suf.dfn[suf.pos[pre.re[sta[tp--]]-m+1]],-1);
}
}
void solve(int u,int pa){
if(pre.re[u])insert1(u,pa),sta1.pb(u);
for(int v:pre.has[u])solve(v,pa);
}
void dfs(int u,int op=0){
for(int v:pre.has[u])if(v^pre.son1[u])dfs(v),clear();
if(pre.son1[u])dfs(pre.son1[u],1);
if(pre.re[u])insert1(u,u),insert(u);
for(int v:pre.has[u])if(v^pre.son1[u]){
solve(v,u);
for(int u:sta1)insert(u);
sta1.clear();
}
}
int main(){
// freopen("1.in","r",stdin);
cin>>n>>m;scanf("%s",a+1);t=log2(n*2)+1;
pre.build(0);suf.build(1);
dfs(1);clear();
for(int i=1;i<=n-m+1;i++)printf("%d ",ans[i]);
return 0;
}