JavaScript實現十大排序演演算法(圖文詳解)

【相關推薦:、】
氣泡排序
排序的效果圖
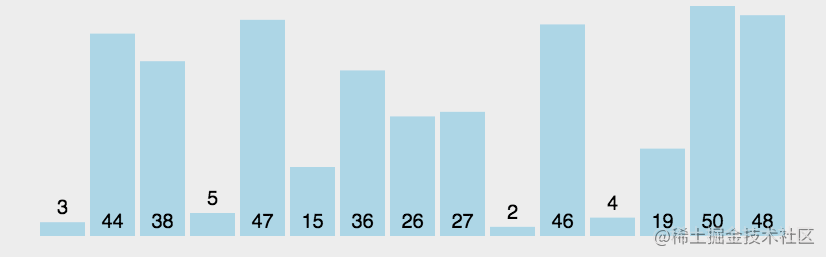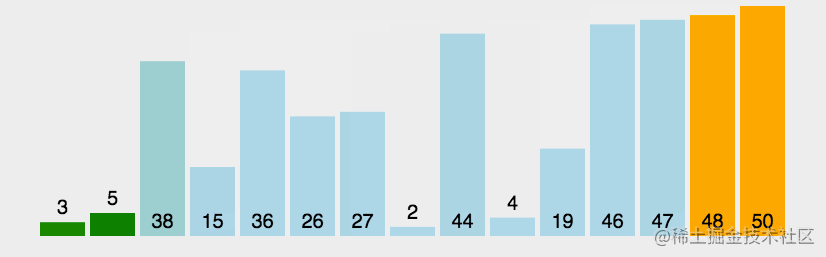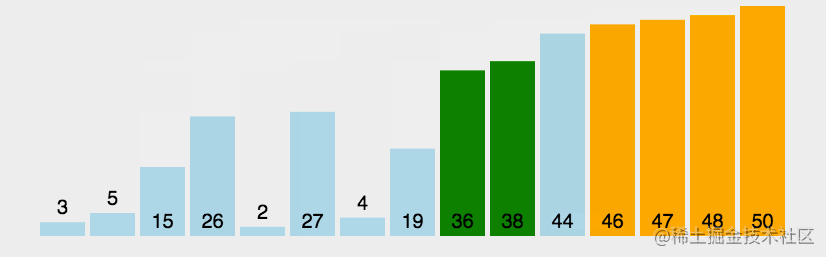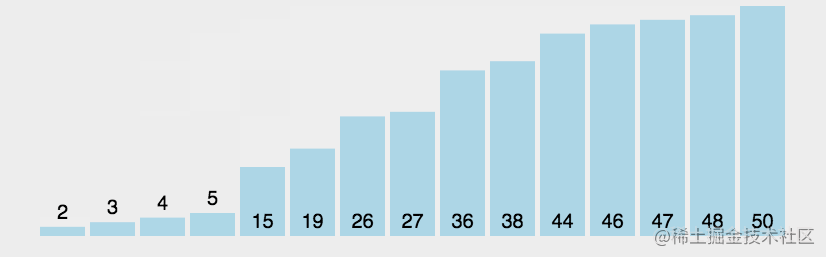
解法
當前解法為升序
氣泡排序的特點,是一個個數進行處理。第i個數,需要與後續的len-i-1個數進行逐個比較。
為什麼是 `len-i-1`個數?
因為陣列末尾的i個數,已經是排好序的,確認位置不變的了。
為什麼確認位置不變,因為它們固定下來之前,已經和前面的數位都一一比較過了。
function bubbleSort(arr){
const len = arr.length;
for(let i = 0; i < len - 1; i++){
for(let j = 0; j < len - i - 1; j++){
if(arr[j] > arr[j+1]){
const tmp = arr[j+1];
arr[j+1] = arr[j];
arr[j] = tmp;
}
}
}
return arr;
}快速排序
概要
快速排序,使用的是分治法的思想。
通過選定一個數位作為比較值,將要排序其他數位,分為 >比較值 和 <比較值,兩個部分。並不斷重複這個步驟,直到只剩要排序的數位只有本身,則排序完成。
效果圖
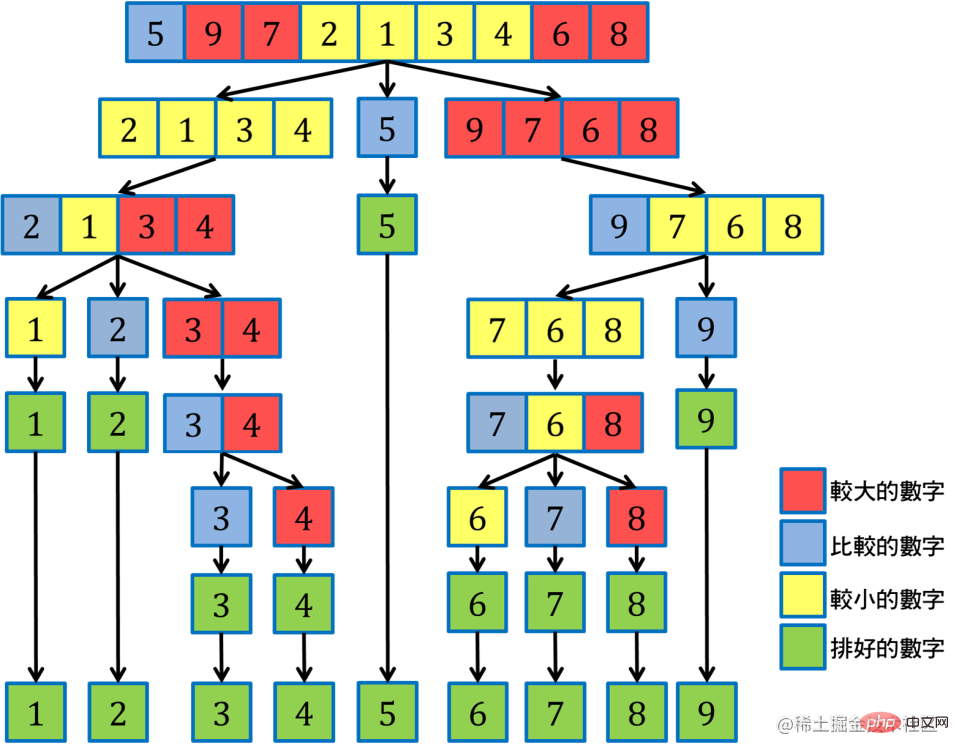
解法
function quickSort(arr){
sort(arr, 0, arr.length - 1);
return arr;
function sort(arr, low, high){
if(low >= high){
return;
}
let i = low;
let j = high;
const x = arr[i]; // 取出比較值x,當前位置i空出,等待填入
while(i < j){
// 從陣列尾部,找出比x小的數位
while(arr[j] >= x && i < j){
j--;
}
// 將空出的位置,填入當前值, 下標j位置空出
// ps:比較值已經快取在變數x中
if(i < j){
arr[i] = arr[j]
i++;
}
// 從陣列頭部,找出比x大的數位
while(arr[i] <= x && i < j){
i++;
}
// 將數位填入下標j中,下標i位置突出
if(i < j){
arr[j] = arr[i]
j--;
}
// 一直迴圈到左右指標i、j相遇,
// 相遇時,i==j, 所以下標i位置是空出的
}
arr[i] = x; // 將空出的位置,填入快取的數位x,一輪排序完成
// 分別對剩下的兩個區間進行遞迴排序
sort(arr, low, i - 1);
sort(arr, i+1, high);
}
}希爾排序
概要
希爾排序是一種插入排序的演演算法,它是對簡單的插入排序進行改進後,更高效的版本。由希爾(Donald Shell)於1959年提出。
特點是利用增量,將陣列分成一組組子序列,然後對子序列進行插入排序。
由於增量是從大到小,逐次遞減,所以也稱為縮小增量排序。
效果圖
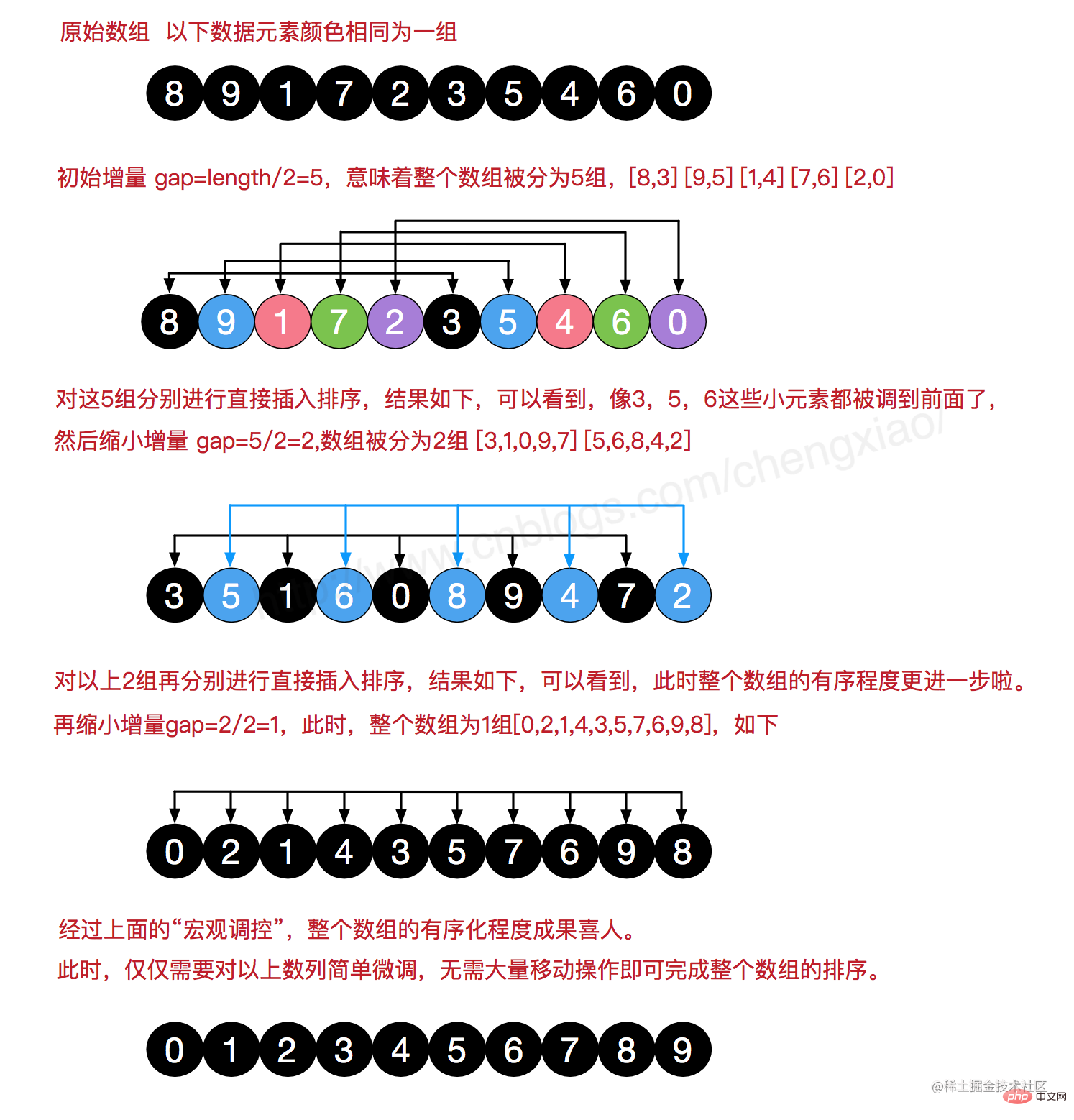
解法
注意點
插入排序時,並不是一個分組內的數位一次性用插入排序完成,而是每個分組交叉進行。
執行插入時,使用交換法
function shellSort(arr){
// 分組規則 gap/2 遞減
for(let gap = Math.floor(arr.length/2); gap > 0; gap = Math.floor(gap/2)){
for(let i = gap; i < arr.length; i++){
let j = i;
// 分組內數位,執行插入排序,
// 當下標大的數位,小於 下標小的數位,進行互動
// 這裡注意,分組內的數位,並不是一次性比較完,需要i逐步遞增,囊括下個分組內數位
while(j - gap >= 0 && arr[j] < arr[j - gap]){
swap(j, j-gap);
j = j - gap;
}
}
}
return arr;
function swap(a, b){
const tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
}執行插入時,使用移動法
function shellSort(arr){
for(let gap = Math.floor(arr.length/2); gap > 0; gap = Math.floor(gap/2)){
for(let i = gap; i < arr.length; i++){
let j = i;
const x = arr[j]; // 快取數位,空出位置
while(j - gap >= 0 && x < arr[j-gap]){
arr[j] = arr[j - gap]; // 將符合條件的數位,填入空出的位置
j = j - gap;
}
arr[j] = x; // 最後,將快取的數位,填入空出的位置
}
}
return arr;
}選擇排序
排序的效果圖
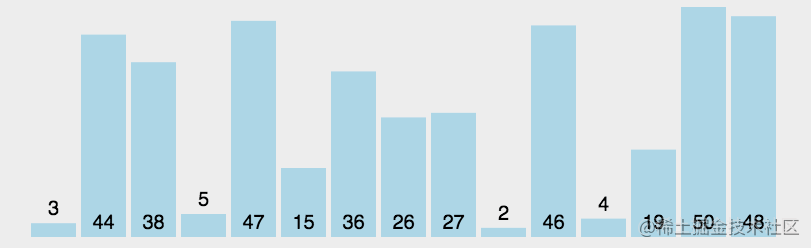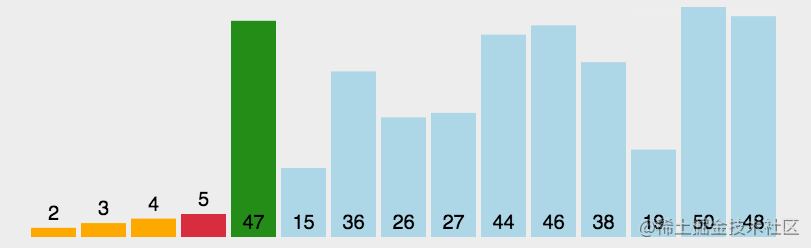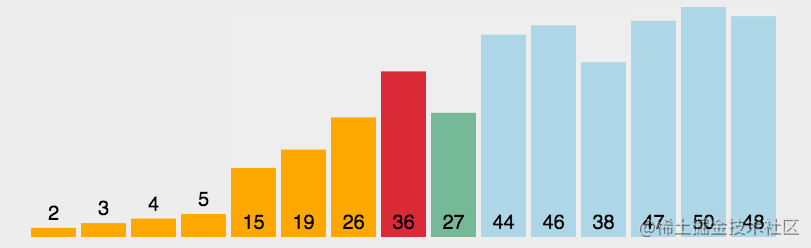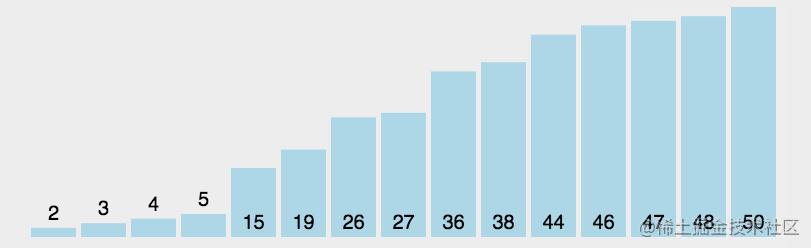
解法
當前解法為升序
function selectionSort(arr){
const len = arr.length;
for(let i = 0; i < len-1; i++){
let minIndex = i;
for(let j = i+1; j < len; j++){
if(arr[j] < arr[minIndex]){
minIndex = j; // 儲存最小數的下標
}
}
const tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
return arr;
}歸併排序
概要
歸併排序,利用分治思想,將大的陣列,分解為小陣列,直至單個元素。然後,使用選擇排序的方式,對分拆的小陣列,進行回溯,並有序合併,直至合併為一個大的陣列。
效果圖
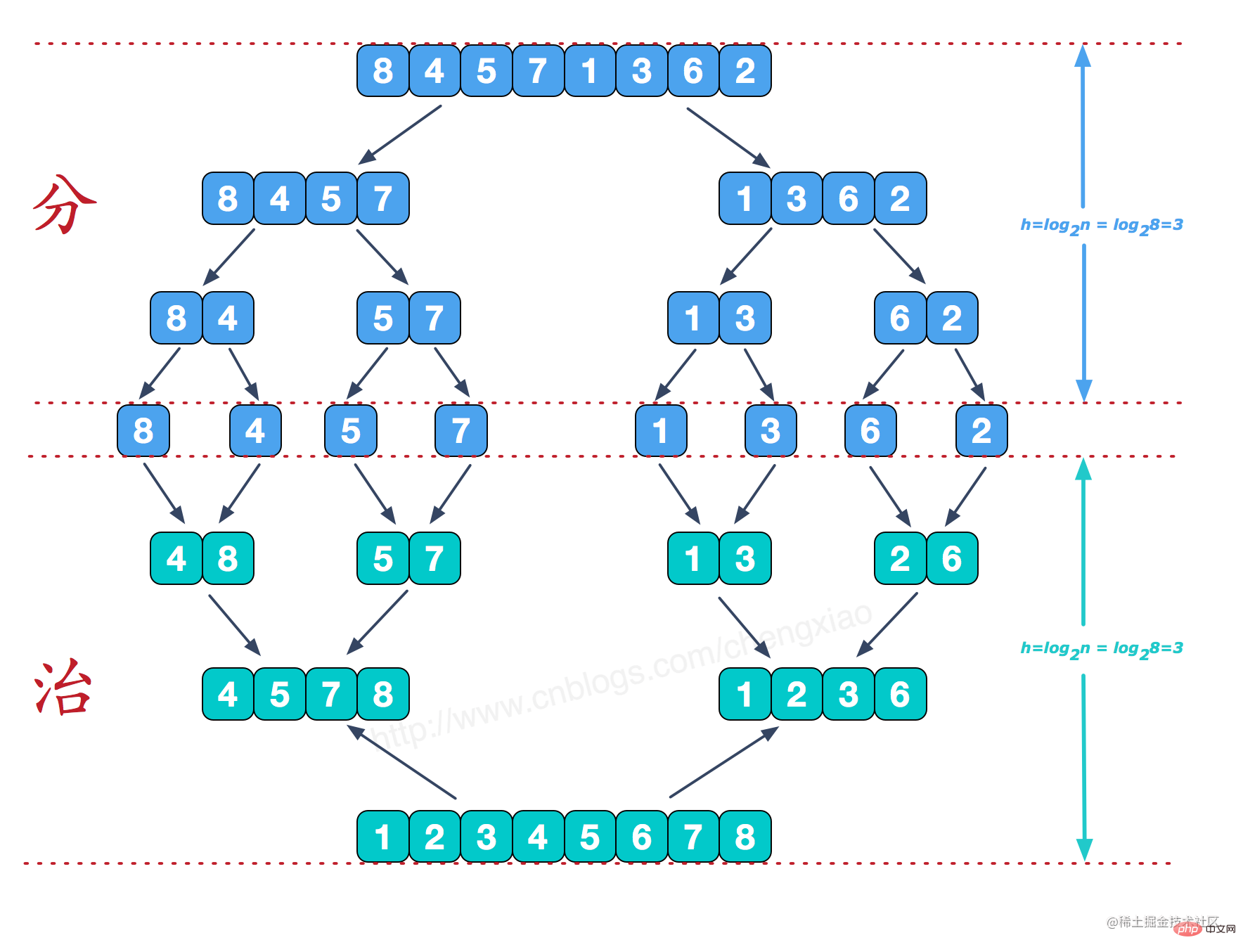
小陣列合併的過程
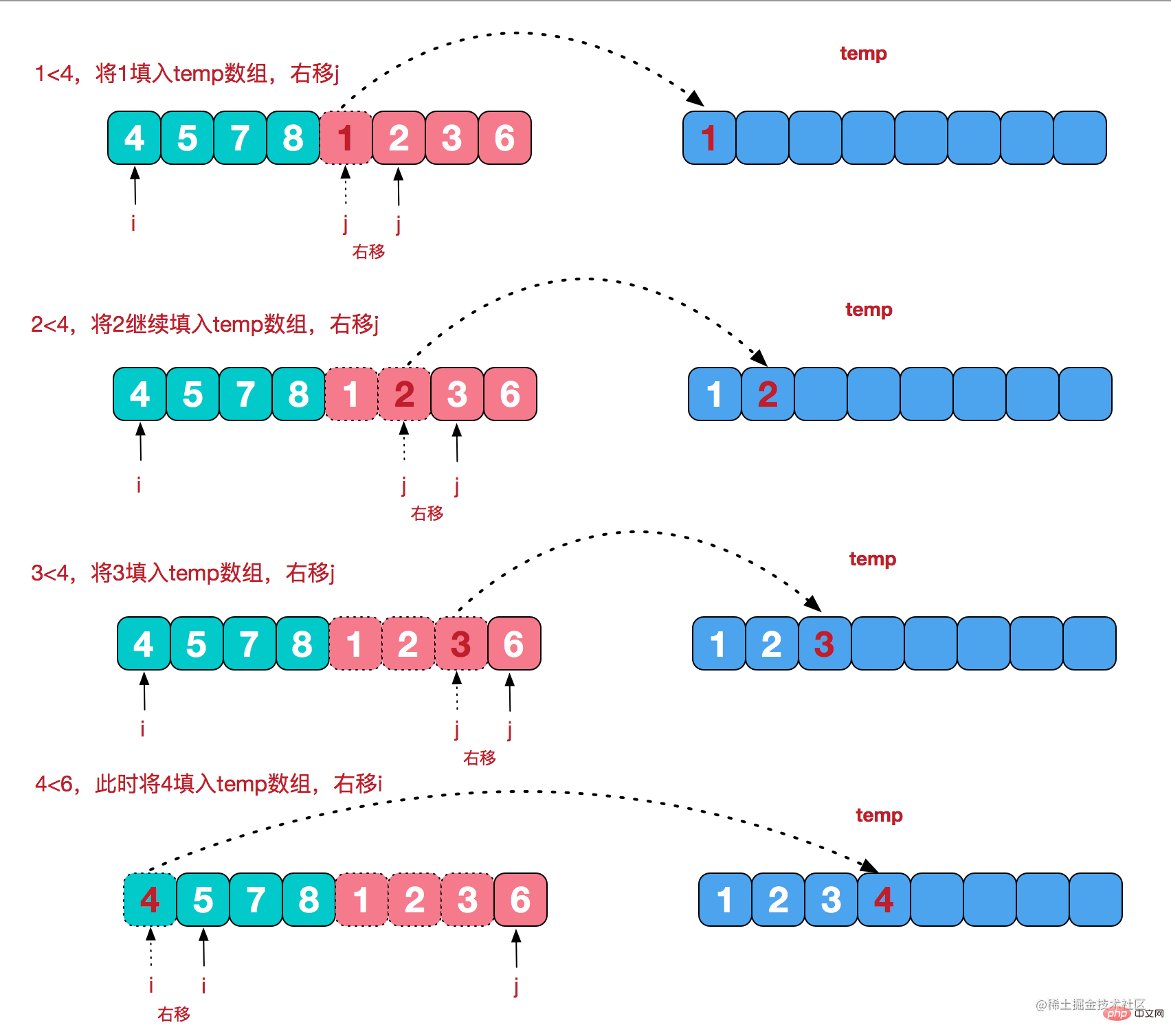
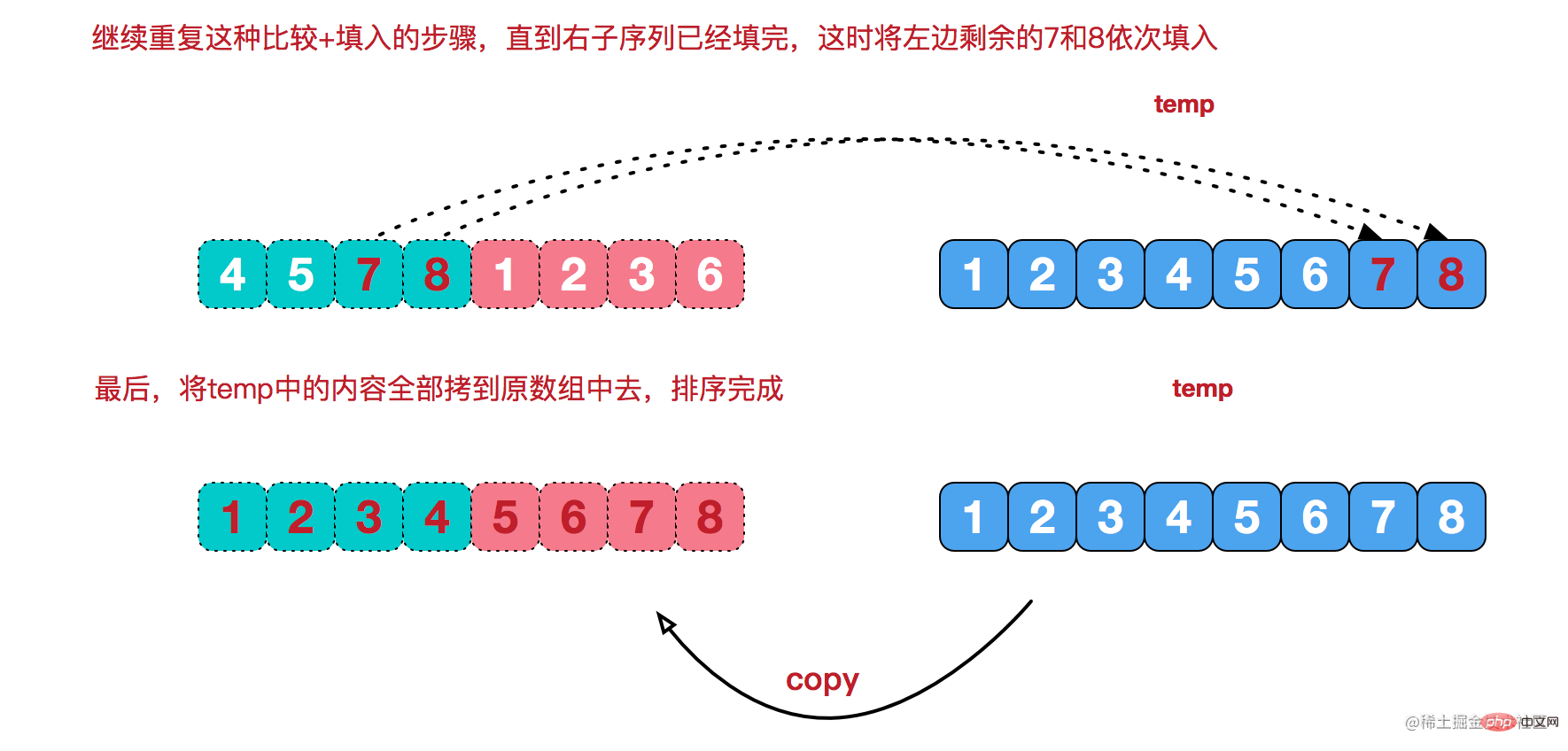
解法
function mergeSort(arr){
return sort(arr, 0, arr.length - 1); // 注意右區間是arr.length - 1
// sort方法,進行遞迴
function sort(arr, left, right){
// 當left !== right時,證明還沒分拆到最小元素
if(left < right){
// 取中間值,分拆為兩個小的陣列
const mid = Math.floor((left+right) / 2);
const leftArr = sort(arr, left, mid);
const rightArr = sort(arr, mid+1, right);
// 遞迴合併
return merge(leftArr, rightArr)
}
// left == right, 已經是最小元素,直接返回即可
return left >= 0 ? [arr[left]] : [];
}
// 合併兩個有序陣列
function merge(leftArr, rightArr){
let left = 0;
let right = 0;
const tmp = [];
// 使用雙指標,對兩個陣列進行掃描
while(left < leftArr.length && right < rightArr.length){
if(leftArr[left] <= rightArr[right]){
tmp.push(leftArr[left++]);
}else{
tmp.push(rightArr[right++]);
}
}
// 合併剩下的內容
if(left < leftArr.length){
while(left < leftArr.length){
tmp.push(leftArr[left++]);
}
}
if(right < rightArr.length){
while(right < rightArr.length){
tmp.push(rightArr[right++]);
}
}
return tmp;
}
}插入排序
排序的效果圖
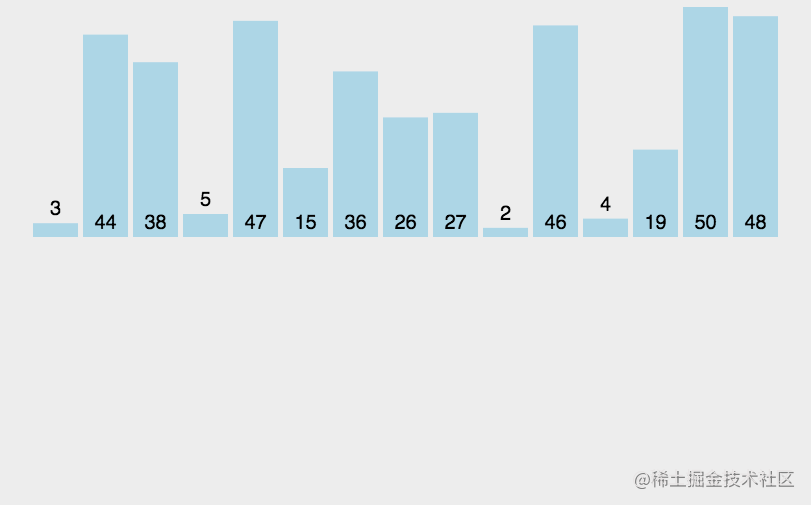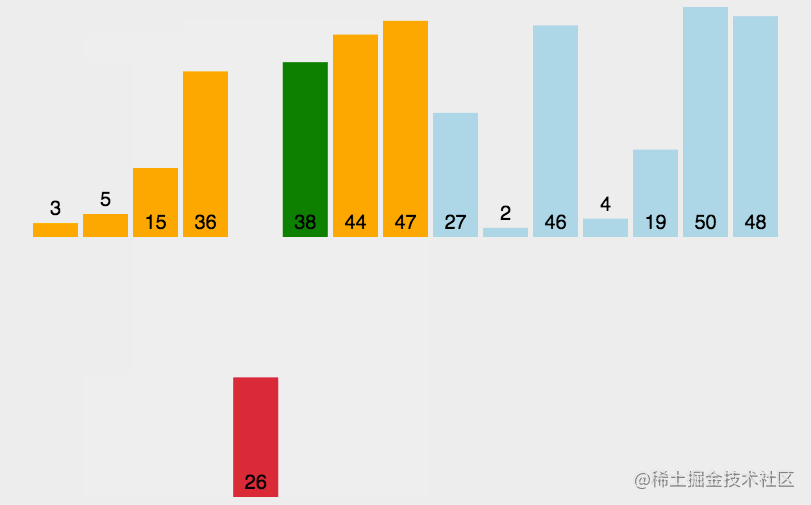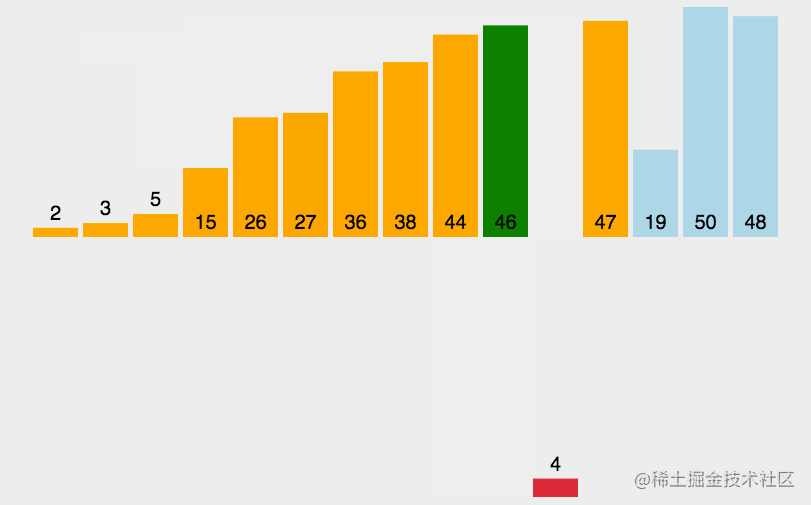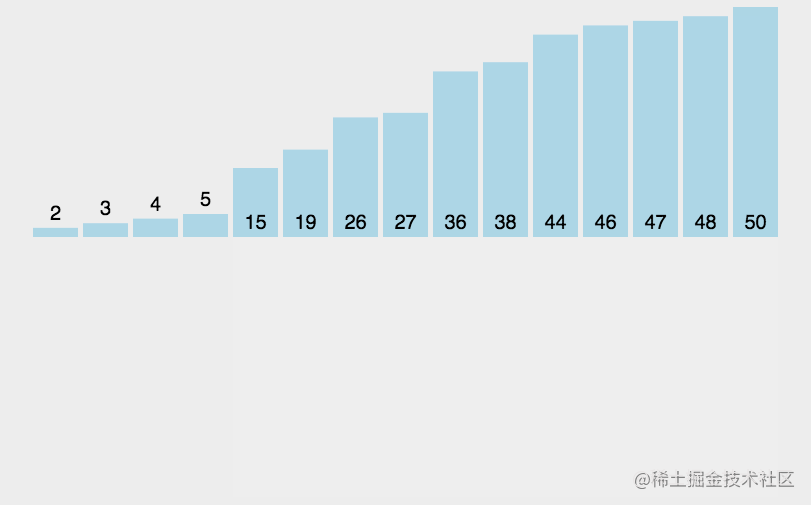
解法
當前解法為升序
function insertionSort(arr){
const len = arr.length;
// 注意,i 從 1 開始
for(let i = 1; i < len; i++){
let preIndex = i - 1;
let current = arr[i];
// 位置i之前,是已排好序的數位,while的作用是找到一個坑位,給當前數位current插入
while(preIndex >= 0 && arr[preIndex] > current){
arr[preIndex+1] = arr[preIndex]; // 對大於current的值,往後移一位,給current的插入騰出位置
preIndex--;
}
arr[preIndex+1] = current;
}
return arr;
}堆排序
概要
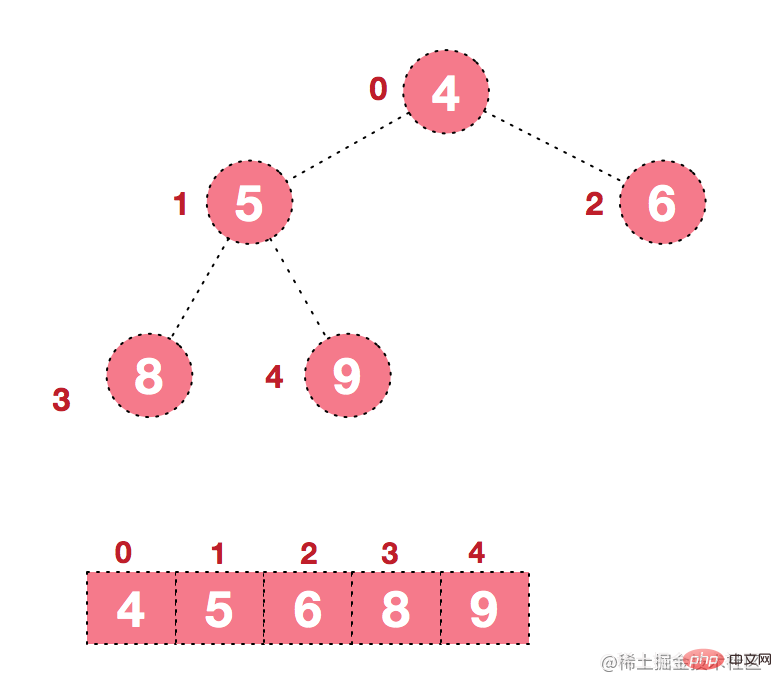
堆的表示形式
邏輯結構的表示如下:
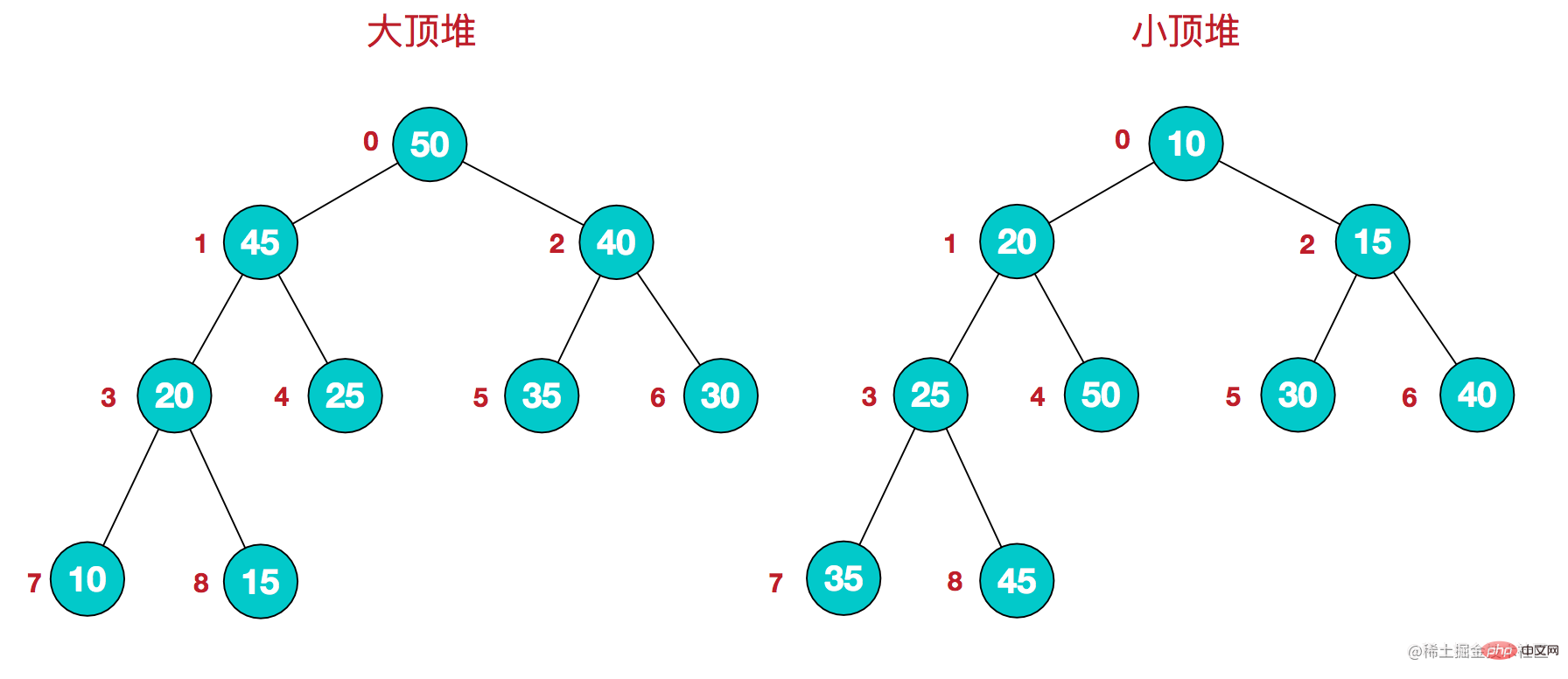
在物理資料層的表示如下:

堆排序,是選擇排序的優化版本,利用資料結構——樹,對資料進行管理。
以大頂堆為例:
通過構建大頂堆
將堆頂的最大數拿出,與堆底的葉子節點進行交換
接著,樹剪掉最大數的葉子
再對堆進行調整,重新變成大頂堆
返回步驟2,以此迴圈,直至取出所有數
效果圖
在實現程式碼時,構建大頂堆時,先保證左右子樹的有序,再逐步擴大到整棵樹。
構建大頂堆
從第一個非葉子節點開始,調整它所在的子樹
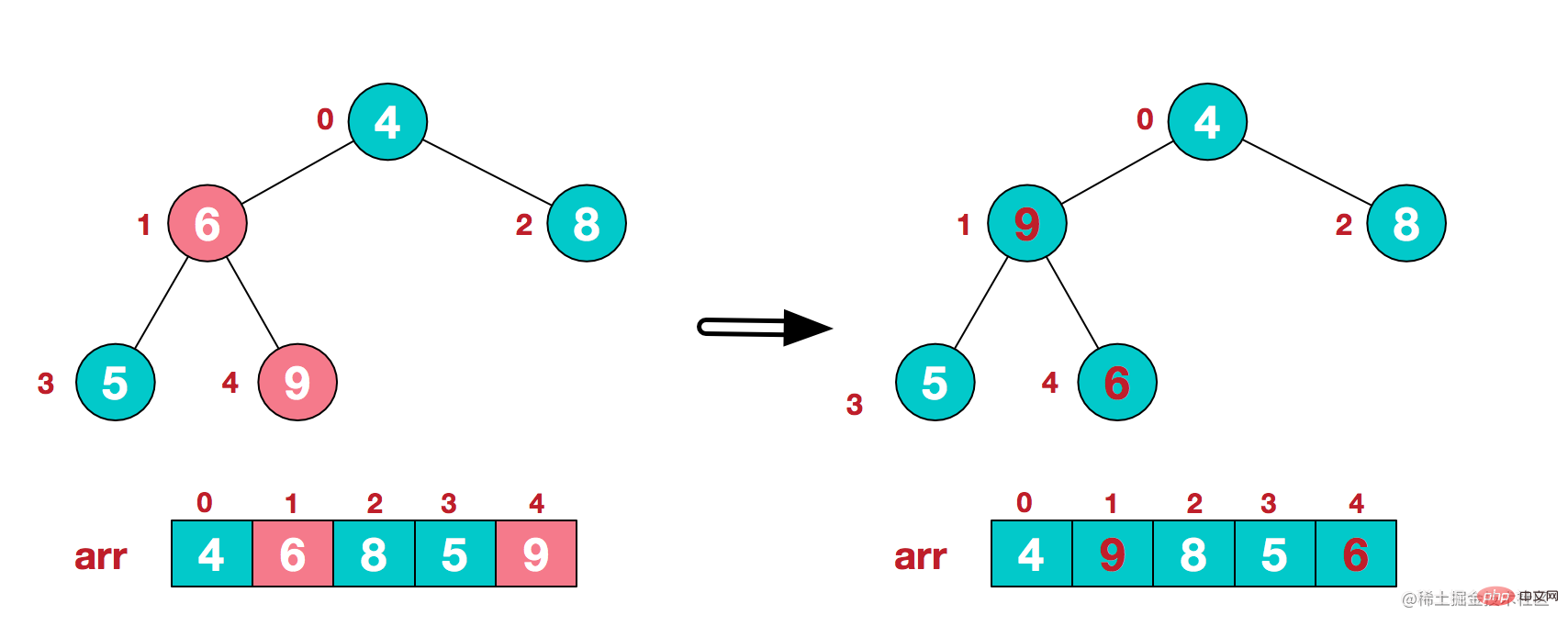
調整下標1節點的子樹後,向上繼續調整它的父節點(下標0)所在的子樹
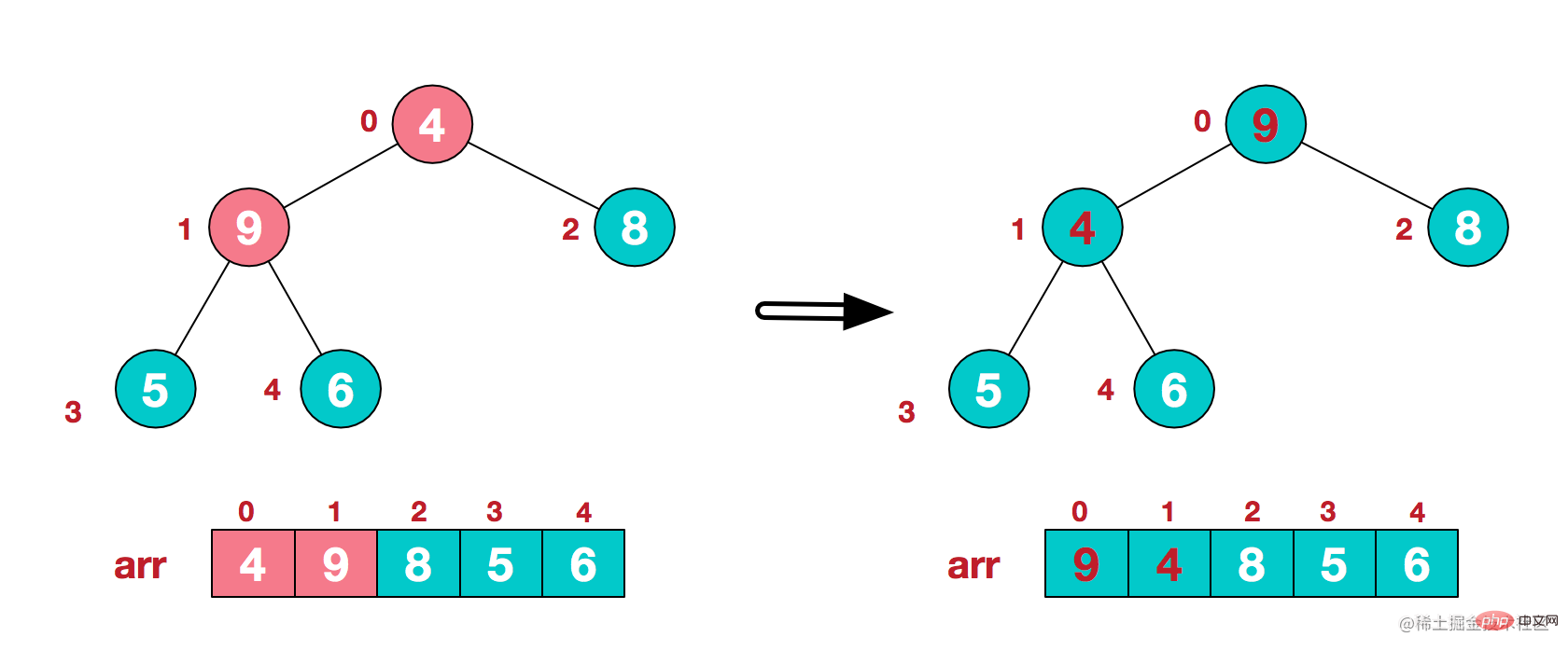
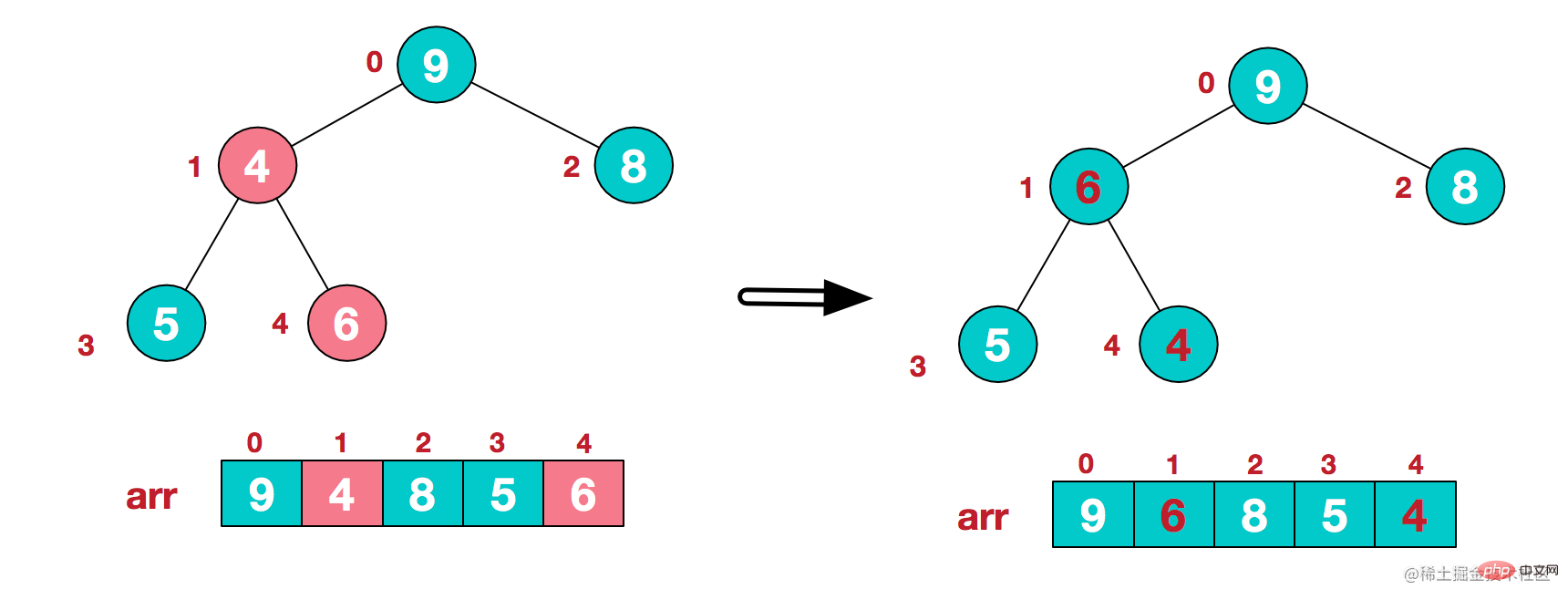
最後,完成整個樹的調整,構建好大頂堆。
逐個抽出堆頂最大值
堆頂數位與最末尾的葉子數位交換,抽出堆頂數位9。
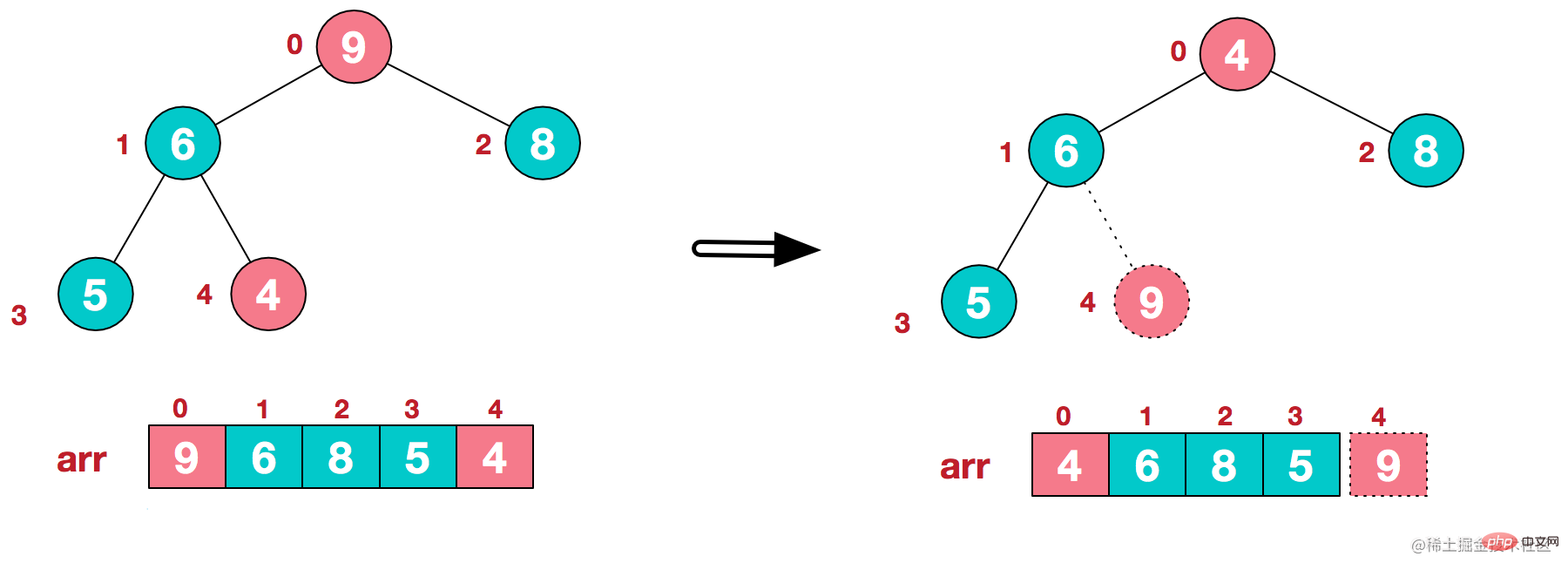
此時,數位9位置固定下來,樹剪掉9所在的葉子。然後,重新構建大頂堆。
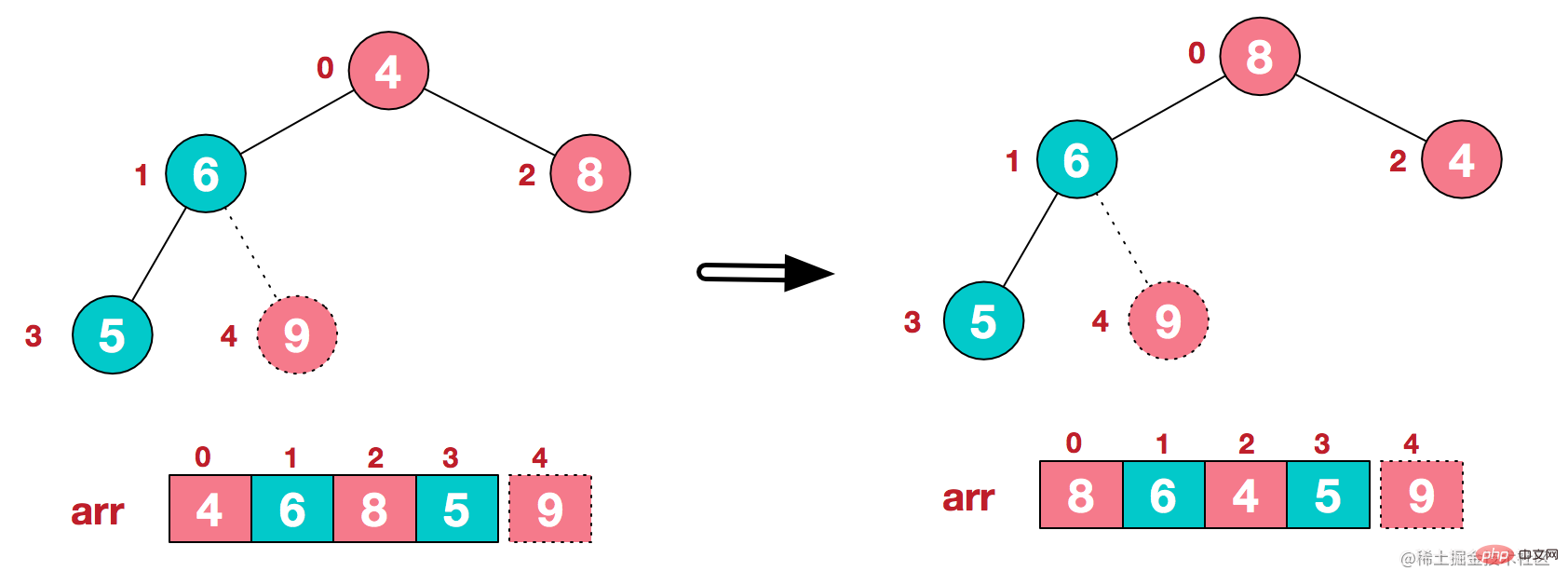
大頂堆構建好後,繼續抽出堆頂數位8,然後再次重新構建大頂堆。
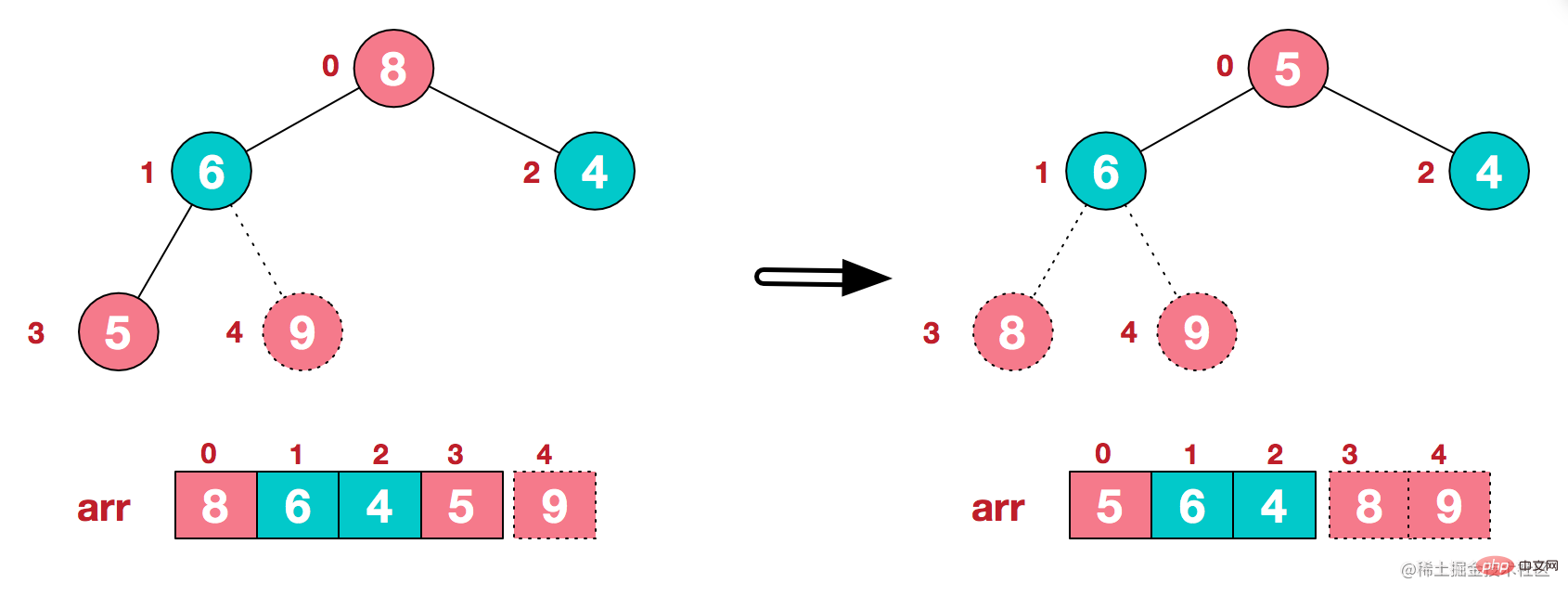
最後,所有節點抽出完成,代表排序已完成。
解法
以大頂堆為例,對陣列進行升序排序
注意點
樹的最後一個非葉子節點:(arr.length / 2) - 1
非葉子節點i的左葉子節點:i*2+1
非葉子節點i的右葉子節點:i*2+2
function heapSort(arr){
// 初次構建大頂堆
for(let i = Math.floor(arr.length/2) - 1; i >= 0; i--){
// 開始的第一個節點是 樹的最後一個非葉子節點
// 從構建子樹開始,逐步調整
buildHeap(arr, i, arr.length);
}
// 逐個抽出堆頂最大值
for(let j = arr.length -1 ; j > 0; j--){
swap(arr, 0, j); // 抽出堆頂(下標0)的值,與最後的葉子節點進行交換
// 重新構建大頂堆
// 由於上一步的堆頂最大值已經交換到陣列的末尾,所以,它的位置固定下來
// 剩下要比較的陣列,長度是j,所以這裡的值length == j
buildHeap(arr, 0, j);
}
return arr;
// 構建大頂堆
function buildHeap(arr, i, length){
let tmp = arr[i];
for(let k = 2*i+1; k < length; k = 2*k+1){
// 先判斷左右葉子節點,哪個比較大
if(k+1 < length && arr[k+1] > arr[k]){
k++;
}
// 將最大的葉子節點,與當前的值進行比較
if(arr[k] > tmp){
// k節點大於i節點的值,需要交換
arr[i] = arr[k]; // 將k節點的值與i節點的值交換
i = k; // 注意:交換後,當前值tmp的下標是k,所以需要更新
}else{
// 如果tmp大於左右子節點,則它們的子樹也不用判斷,都是小於當前值
break;
}
}
// i是交換後的下標,更新為tmp
arr[i] = tmp;
}
// 交換值
function swap(arr, i, j){
const tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}計數排序
概要
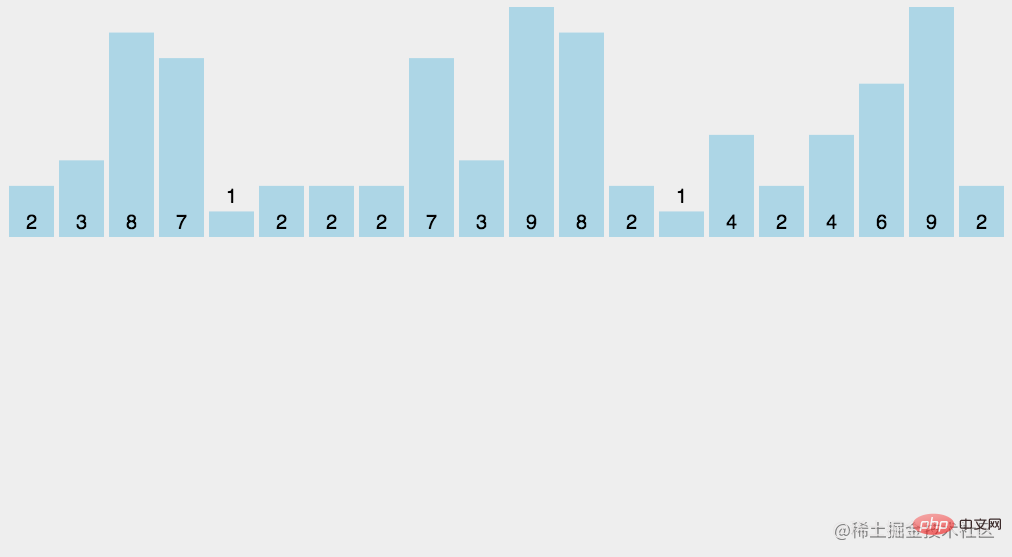
計數排序的要點,是開闢一塊連續格子組成的空間,給資料進行儲存。
將陣列中的數位,依次讀取,存入其值對應的下標中。
儲存完成後,再按照空間的順序,依次讀取每個格子的資料,輸出即可。
所以,計數排序要求排序的資料,必須是有範圍的整數。
效果圖
解法
function countingSort(arr){
let maxValue = Number.MIN_VALUE;
let minValue = Number.MAX_VALUE;
let offset = 0; // 位移,用於處理負數
const result = [];
// 取出陣列的最大值, 最小值
arr.forEach(num => {
maxValue = num > maxValue ? num : maxValue;
minValue = num > minValue ? minValue : num;
});
if(minValue < 0){
offset = -minValue;
}
const bucket = new Array(maxValue+offset+1).fill(0); // 初始化連續的格子
// 將陣列中的每個數位,根據值放入對應的下標中,
// `bucket[num] == n`格子的意義:存在n個數位,值為num
arr.forEach(num => {
bucket[num+offset]++;
});
// 讀取格子中的數
bucket.forEach((store, index) => {
while(store--){
result.push(index - offset);
}
});
return result;
}桶排序
概要
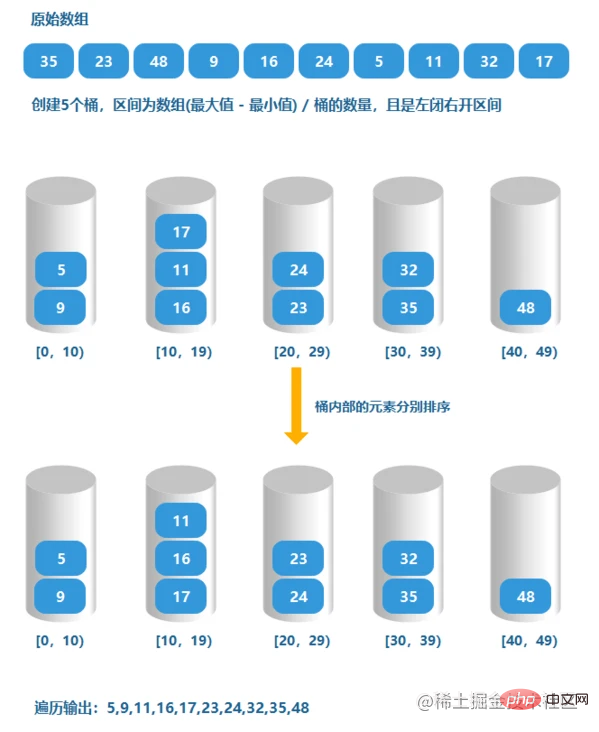
桶排序是計數排序的優化版,原理都是一樣的:分治法+空間換時間。
將陣列進行分組,減少排序的數量,再對子陣列進行排序,最後合併即可得到結果。
效果圖
解法
對桶內數位的排序,本文采用的是桶排序遞迴。其實它的本質是退化到計數排序。
function bucketSort(arr, bucketSize = 10){
// bucketSize 每個桶可以存放的數位區間(0, 9]
if(arr.length <= 1){
return arr;
}
let maxValue = arr[0];
let minValue = arr[0];
let result = [];
// 取出陣列的最大值, 最小值
arr.forEach(num => {
maxValue = num > maxValue ? num : maxValue;
minValue = num > minValue ? minValue : num;
});
// 初始化桶的數量
const bucketCount = Math.floor((maxValue - minValue)/bucketSize) + 1; // 桶的數量
// 初始化桶的容器
// 注意這裡的js語法,不能直接fill([]),因為生成的二維下標陣列,是同一個地址
const buckets = new Array(bucketCount).fill(0).map(() => []);
// 將數位按照對映的規則,放入桶中
arr.forEach(num => {
const bucketIndex = Math.floor((num - minValue)/bucketSize);
buckets[bucketIndex].push(num);
});
// 遍歷每個桶記憶體儲的數位
buckets.forEach(store => {
// 桶內只有1個數位或者空桶,或者都是重複數位,則直接合併到結果中
if(store.length <= 1 || bucketSize == 1){
result = result.concat(store);
return;
}
// 遞迴,將桶內的數位,再進行一次劃分到不同的桶中
const subSize = Math.floor(bucketSize/2); // 減少桶內的數位區間,但必須是最少為1
const tmp = bucketSort(store, subSize <= 1 ? 1: subSize);
result = result.concat(tmp);
});
return result;
}基數排序
概述
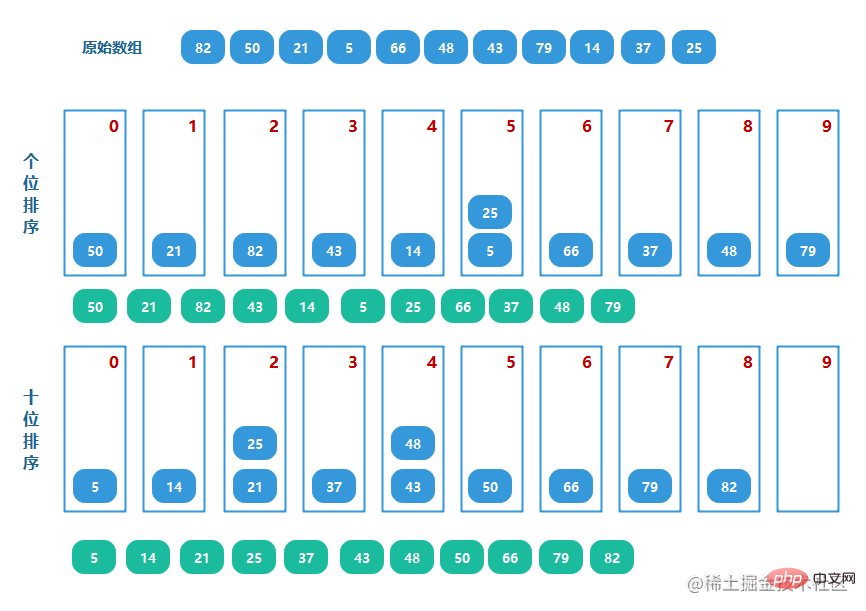
基數排序,一般是從右到左,對進位制位上的數位進行比較,存入[0, 9]的10個桶中,進行排序。
從低位開始比較,逐位進行比較,讓每個進位制位(個、十、百、千、萬)上的數位,都能放入對應的桶中,形成區域性有序。
為什麼10個桶?
因為十進位制數,是由0-9數位組成,對應的進位制位上的數位,都會落在這個區間內,所以是10個桶。
基數排序有兩種方式:
MSD 從高位開始進行排序
LSD 從低位開始進行排序
效果圖
解法
當前解法,只適用正整數的場景。
負數場景,需要加上偏移量解決。可參考 計數排序 的解法。
function radixSort(arr){
let maxNum = arr[0];
// 求出最大的數位,用於確定最大進位制位
arr.forEach(num => {
if(num > maxNum){
maxNum = num;
}
});
// 獲取最大數位有幾位
let maxDigitNum = 0;
while(maxNum > 0){
maxNum = Math.floor(maxNum / 10);
maxDigitNum++;
}
// 對每個進位制位上的數進行排序
for(let i = 0; i < maxDigitNum; i++){
let buckets = new Array(10).fill(0).map(() => []); // 初始化10個桶
for(let k = 0; k < arr.length; k++){
const bucketIndex = getDigitNum(arr[k], i); // 獲取當前進位制位上的數位
buckets[bucketIndex].push(arr[k]); // 排序的數位放入對應桶中
}
// 所有數位放入桶中後,現從0-9的順序將桶中的數位取出
const res = [];
buckets.forEach(store => {
store.forEach(num => {
res.push(num); // 注意這裡,先存入桶中的數位,先取出,這樣才能保持區域性有序
})
});
arr = res;
}
return arr;
/**
求出數位每個進位制位上的數位,只支援正整數
@param num 整數
@param digit 位數,從0開始
*/
function getDigitNum(num, digit){
return Math.floor(num / Math.pow(10, digit) % 10)
}
}演演算法複雜度
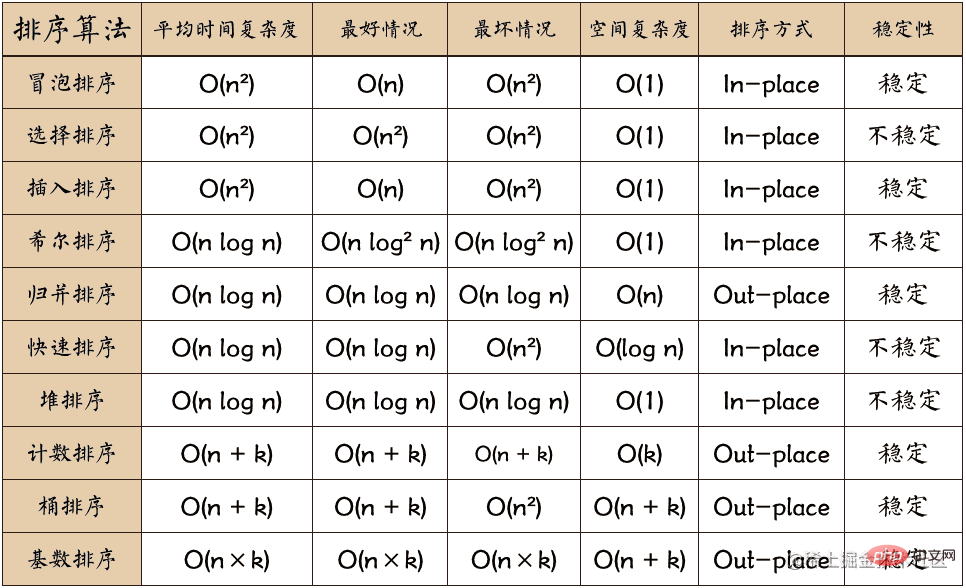
【相關推薦:、】
以上就是JavaScript實現十大排序演演算法(圖文詳解)的詳細內容,更多請關注TW511.COM其它相關文章!
