最近公共祖先（LCA）學習筆記 | P3379 【模板】最近公共祖先（LCA）題解

研究了LCA，寫篇筆記記錄一下。

講解使用例題 P3379 【模板】最近公共祖先（LCA）。

什麼是LCA

最近公共祖先簡稱 LCA（Lowest Common Ancestor）。兩個節點的最近公共祖先，就是這兩個點的公共祖先裡面，離根最遠的那個。
—— 摘自 OI Wiki

比如下圖紅、黃兩點的LCA就是綠點。

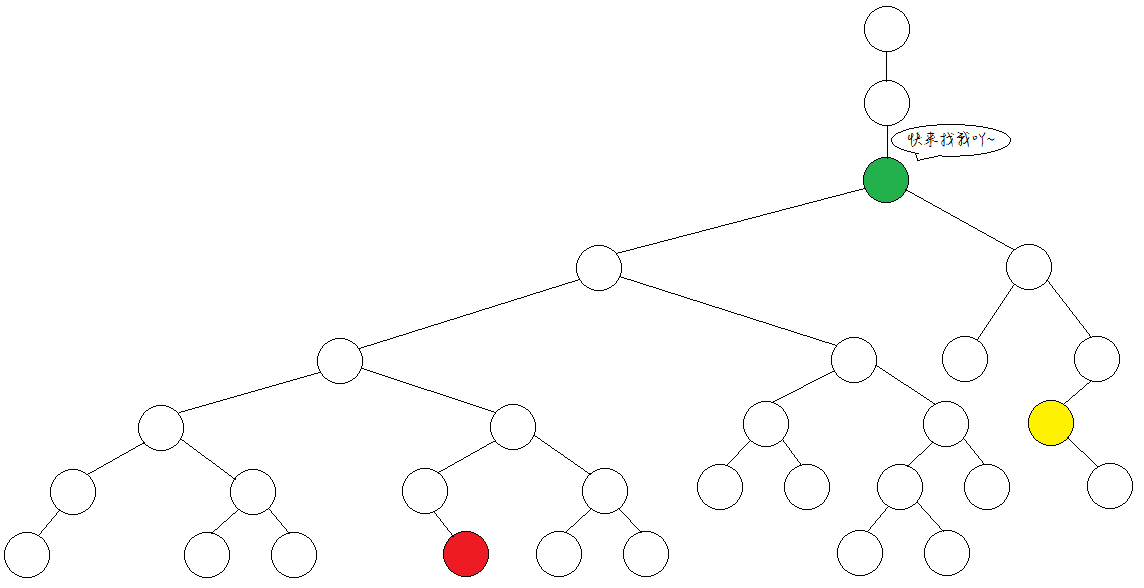
LCA的幾種實現方式

向上標記法

從 x 點一直向上走直到到達根節點，在走的過程中標記所有經過的點。

從 y 點一直向根節點走，遇到的第一個標記過的點即為兩點的LCA。

~~程式碼略~~

樹上倍增法

首先，我們將要求、lca的兩點跳到同一深度，如下圖：

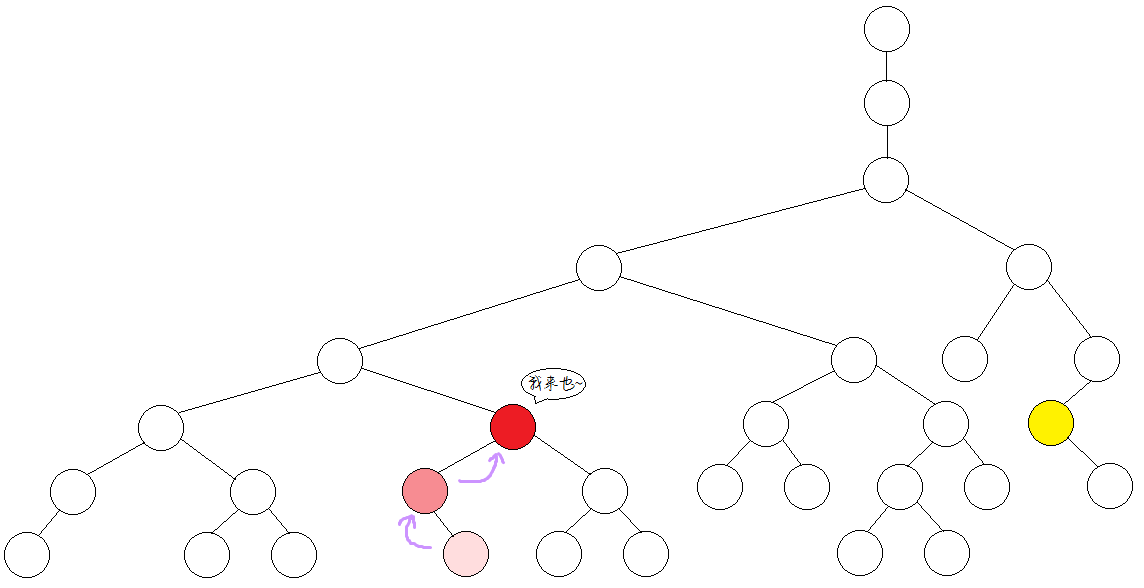
然後兩點同時向上從大到小倍增，直到到的兩點不相同，繼續往上跳。

先嚐試向能跳的最遠處跳（4步）。

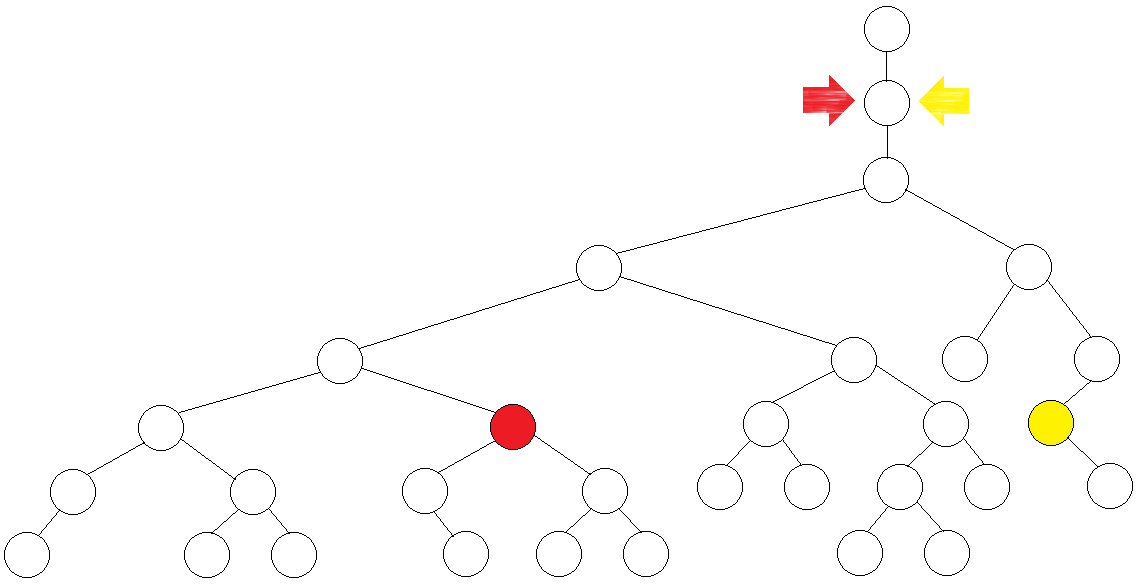
我們發現兩個點在同處匯合，不行，考慮少跳一半（2步）。

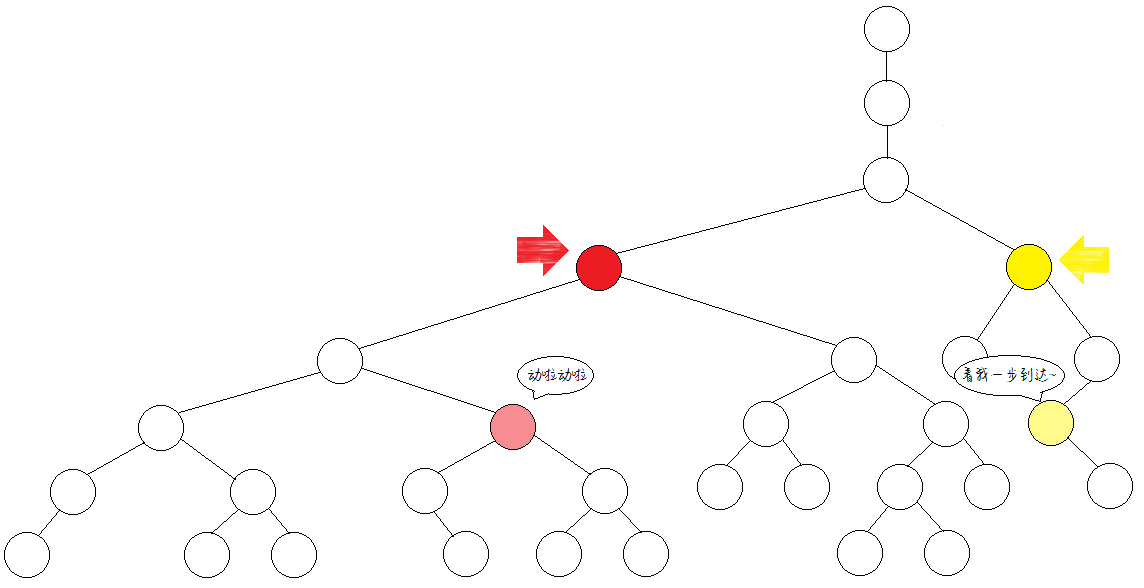
不同點，跳上。繼續少跳一半（1步）。

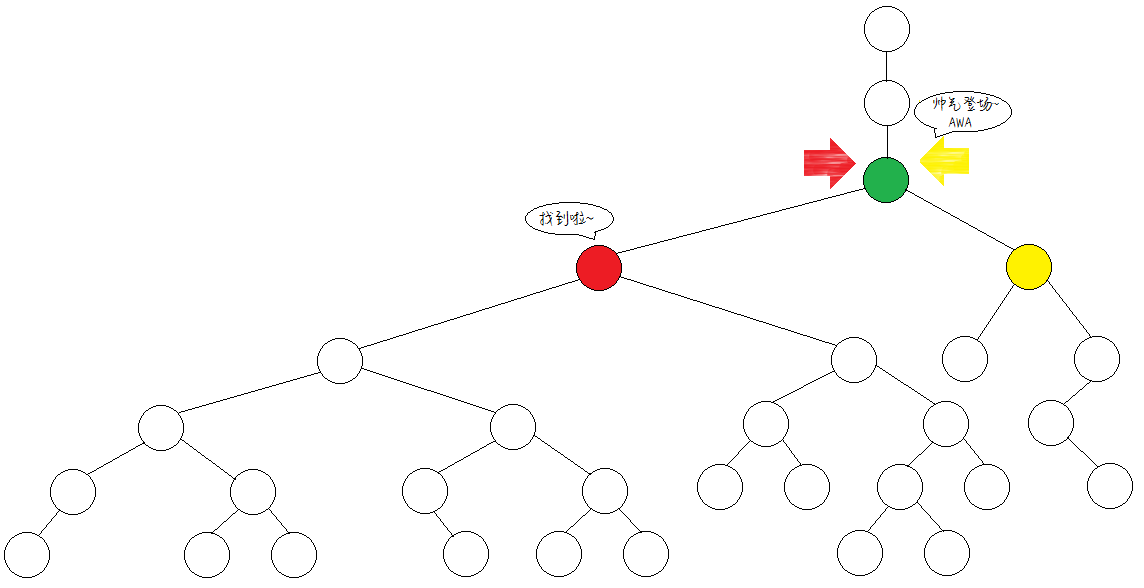
同一個點，不跳。

此時，所有的跳躍嘗試結束。由於目前兩點不在同處，故再往上跳一步。

於是就找到這兩個點的LCA啦！

（是不是講的雲裡霧裡的，結合程式碼理解一下吧~）

程式碼實現

dfs獲取每個點的深度

int p[N], dep[N];
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) { //我用鄰接表存的圖
		int v = e[i].to;
		if (v == f) continue;
		dep[v] = dep[x] + 1;
		dfs(v, x);
	}
}

dep[s] = 1;
dfs(s, s); //將起點的父節點設為自己，這樣跳多了也不會出鍋

預處理倍增跳到的點

for (int i = 1; i <= n; i++) f[0][i] = p[i];
for (int j = 1; j <= lg; j++) // 跳 2^j 步   lg 為 log2(n)
	for (int i = 1; i <= n; i++) // 第 i 個點
		f[j][i] = f[j - 1][f[j - 1][i]];
// 跳 2^j 步到的點即為先跳 2^(j-1) 步再跳 2^(j-1) 步到的點

處理LCA

（~~沒有寫成函數QAQ~~）

int a = read(), b = read();
if (dep[a] > dep[b]) swap(a, b); //使 a 的深度小於等於 b
for (int i = lg; i >= 0; i--)
	if (dep[f[i][b]] >= dep[a]) b = f[i][b]; //將 a 與 b 跳到同一深度
for (int i = lg; i >= 0; i--) //從最遠的距離開始嘗試 （跳 2^i 步）
	if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a]; //不是同一個點就跳上去
if (a != b) a = p[a];
//結束後不是同一個點，那麼LCA就是目前這個點的父節點，所以也可以寫成 b = p[b] 然後輸出 b
printf("%d\n", a);

為什麼嘗試跳只用從 log2(n) 迴圈一遍到 0 就行？

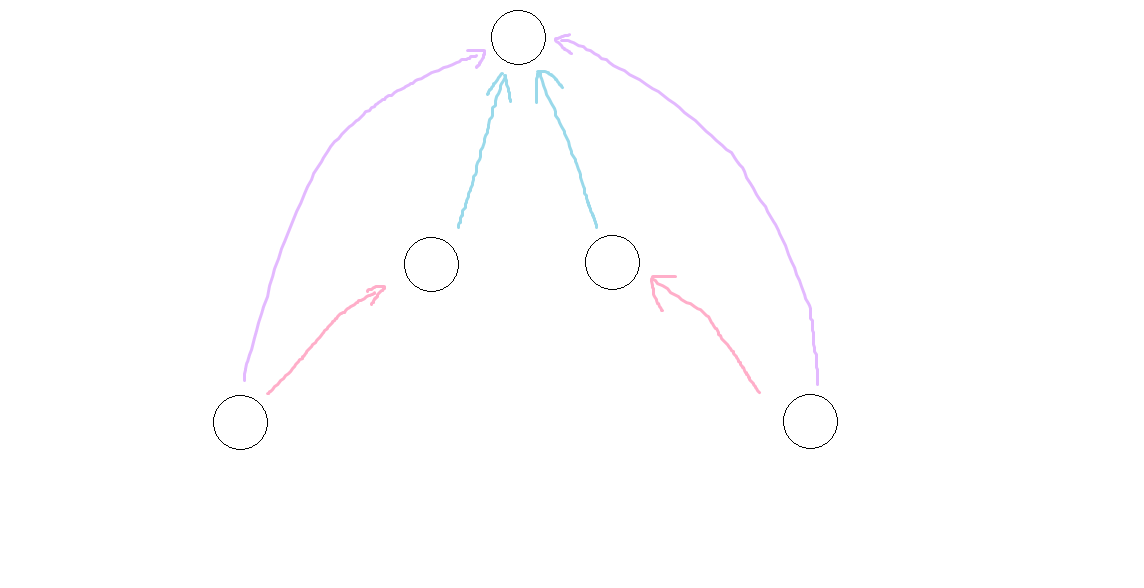
按照程式碼思路，我們會先嚐試沿紫色路徑跳 2^j 步，由於不成功，我們折半跳 2^(j-1) 步，沿粉邊跳上。

此時若在沿藍邊跳 2^(j-1) 步，又跳到了原來粉邊指向的點，我們已經知道那個點不行，所以不用嘗試跳上，而應該繼續嘗試跳 2^(j-2) 步。

完整程式碼（點選檢視）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read() {
	ll s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
	return s * w;
}
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge {
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
}
int p[N], dep[N];
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		dep[v] = dep[x] + 1;
		dfs(v, x);
	}
}
int f[19][N], lg;
int main() {
	n = read(), m = read(), s = read();
	lg = log2(n);
	for (int i = 1; i < n; i++) {
		int u = read(), v = read();
		addedge(u, v), addedge(v, u);
	}
	dep[s] = 1;
	dfs(s, s);
	for (int i = 1; i <= n; i++) f[0][i] = p[i];
	for (int j = 1; j <= lg; j++) 
		for (int i = 1; i <= n; i++) 
			f[j][i] = f[j - 1][f[j - 1][i]];
	while (m--) {
		int a = read(), b = read();
		if (dep[a] > dep[b]) swap(a, b);
		for (int i = lg; i >= 0; i--)
			if (dep[f[i][b]] >= dep[a]) b = f[i][b];
		for (int i = lg; i >= 0; i--) 
			if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a];
		if (a != b) a = p[a];
		printf("%d\n", a);
	}
	return 0;
}

LCA的Tarjan演演算法

本質來說，其實就是用並查集對「向上標記法」進行優化。

注意：操作是離線的。

從根節點開始進行 DFS，對於每個搜到的點打上標記，在回溯時將該結點併入其父節點的集合，具體操作見下。

如何離線？

我們先把 m 次詢問都讀入，然後再相關的兩個結點上分別掛上詢問。

為什麼要兩點都掛上詢問

因為我們並不知道兩個點誰先存取誰後存取，不好處理。

比如現在給一棵樹，詢問紅、黃兩點的 LCA 。

我們對這棵樹進行 DFS，目前已經搜到了黃點，上方的三個不同深度的橙點表示 DFS 過程中棧裡的點。

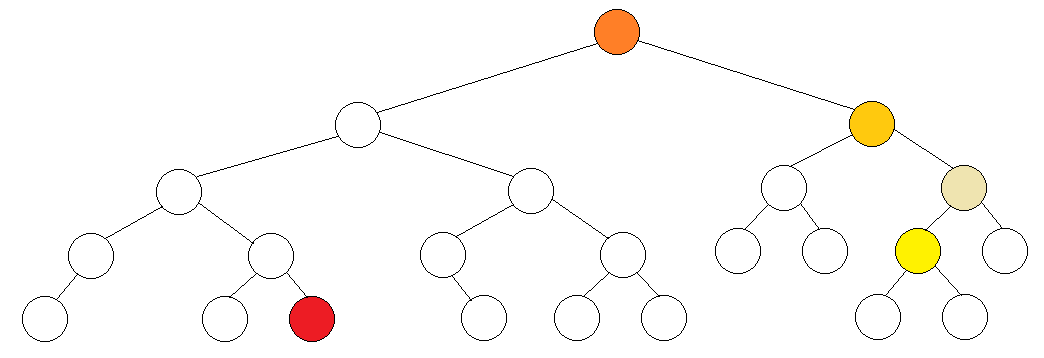
由於已經搜過了根節點的左子樹，所以紅點已打過標記。根節點的左子樹與根節點屬於一個集合，第二層的黃點的左子樹與它自己屬於一個集合。

現在在黃點上打個標記，發現黃點上掛的關於紅點的詢問可以處理了（兩點都已搜到）。

紅、黃兩點的LCA即為紅點所在集合的根節點，即圖中樹的根節點。

（~~講的有億點點亂誒~~）

程式碼實現

儲存詢問

struct node { //為了保證輸出順序，不僅要把詢問掛在點上，還要額外存一下
	int x, y, ans;
} ask[N];
vector <int> g[N]; //每個點上掛的詢問

for (int i = 1; i <= m; i++) {
	ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
	g[ask[i].x].push_back(i);
	g[ask[i].y].push_back(i);
}

int p[N];
bool vis[N]; //存取標記
int r[N]; //一個集合實際的根節點（並查集是按秩合併的，根節點不能保證是我們要的根節點）
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		vis[v] = 1;
		for (int j : g[v]) { //遍歷所有詢問 
			int o = ask[j].x;
			if (o == v) o = ask[j].y;
			if (!vis[o]) continue;
			ask[j].ans = r[a.root(o)]; //記錄詢問答案
		}
		dfs(v, x);
		a.merge(x, v); //合併兩個集合
		r[a.root(x)] = x; //標記實際根節點
	}
}

vis[s] = 1;
dfs(s, s);

完整程式碼（點選檢視）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read() {
	ll s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
	return s * w;
}
const int N = 500010;
int n, m, s;
struct Disjoint_Set {
	int p[N], size[N];
	void build() {
		for (int i = 1; i <= n; i++) p[i] = i, size[i] = 1;
	}
	int root(int x) {
		if (p[x] != x) return p[x] = root(p[x]);
		return x;
	}
	void merge(int x, int y) {
		x = root(x), y = root(y);
		if (size[x] > size[y]) swap(x, y);
		p[x] = y;
		size[y] += size[x];
	}
	bool check(int x, int y) {
		x = root(x), y = root(y);
		return x == y;
	}
} a;
int last[N], cnt;
struct edge {
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
}
struct node {
	int x, y, ans;
} ask[N];
vector <int> g[N];
int p[N];
bool vis[N];
int r[N];
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		vis[v] = 1;
		for (int j : g[v]) {
			int o = ask[j].x;
			if (o == v) o = ask[j].y;
			if (!vis[o]) continue;
			ask[j].ans = r[a.root(o)]; 
		}
		dfs(v, x);
		a.merge(x, v);
		r[a.root(x)] = x;
	}
}
int main() {
	n = read(), m = read(), s = read();
	a.build();
	for (int i = 1; i <= n; i++) {
		r[i] = i;
	}
	for (int i = 1; i < n; i++) {
		int u = read(), v = read();
		addedge(u, v), addedge(v, u);
	}
	for (int i = 1; i <= m; i++) {
		ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
		g[ask[i].x].push_back(i);
		g[ask[i].y].push_back(i);
	}
	vis[s] = 1;
	dfs(s, s);
	for (int i = 1; i <= m; i++) printf("%d\n", ask[i].ans);
	return 0;
}

LCA轉RMQ

~~先貼程式碼吧，講解後續再補~~

~~咕咕咕~~

完整程式碼（點選檢視）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read() {
	ll s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
	return s * w;
}
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge{
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
}
int dep[N], a[N << 1], ed, fst[N];
void dfs(int x, int f) {
	a[++ed] = x;
	if (!fst[x]) fst[x] = ed;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		dep[v] = dep[x] + 1;
		dfs(v, x);
		a[++ed] = x;
	}
}
int f[21][N << 1], lg; 
int main() {
	n = read(), m = read(), s = read();
	lg = log2(n) + 1;
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		addedge(x, y), addedge(y, x);
	}
	dep[s] = 1;
	dfs(s, s);
	for (int i = 1; i <= ed; i++) f[0][i] = i;
	for (int j = 1; j <= lg; j++) {
		for (int i = 1; i <= ed - (1 << j) + 1; i++) {
			int i2 = i + (1 << (j - 1));
			if (dep[a[f[j - 1][i]]] < dep[a[f[j - 1][i2]]]) f[j][i] = f[j - 1][i];
			else f[j][i] = f[j - 1][i2];
		}
	}
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read();
		if (fst[x] > fst[y]) swap(x, y);
		int len = fst[y] - fst[x] + 1, ans;
		int lg2 = log2(len);
		int i2 = fst[y] - (1 << lg2) + 1;
		if (dep[a[f[lg2][fst[x]]]] < dep[a[f[lg2][i2]]]) ans = a[f[lg2][fst[x]]];
		else ans = a[f[lg2][i2]];
		printf("%d\n", ans);
	} 
	return 0;
}