Python資料分析--Numpy常用函數介紹(9)-- 與線性代數有關的模組linalg

numpy.linalg 模組包含線性代數的函數。使用這個模組，可以計算逆矩陣、求特徵值、解線性方程組以及求解行列式等。
一、計算逆矩陣

線性代數中，矩陣A與其逆矩陣A ^(-1)相乘後會得到一個單位矩陣I。該定義可以寫為A *A ^(-1) =1。numpy.linalg 模組中的 inv 函數可以計算逆矩陣。

1) 用 mat 函數建立範例矩陣

import numpy as np
import matplotlib.pyplot as plt

A = np.mat("0 1 2;1 0 3;4 -3 8")

2)用 inv 函數計算逆矩陣

inverse = np.linalg.inv(A)
print("inverse of A\n", inverse)

執行結果如下：

A
 [[ 0  1  2]
 [ 1  0  3]
 [ 4 -3  8]]
inverse of A
 [[-4.5  7.  -1.5]
 [-2.   4.  -1. ]
 [ 1.5 -2.   0.5]]

3）可能通過原矩陣和逆矩陣相乘的結果來驗證

print ("Check\n", A * inverse) #驗證計算，原矩陣和逆矩陣相乘的，單位矩陣

結果：

Check
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

二、求解線性方程組

線性議程組 Ax=b

1)分另建立矩陣A和陣列b

A = np.mat("1 -2 1;0 2 -8;-4 5 9") #用mat()函數建立範例矩陣
print("A\n", A)
b = np.array([0, 8, -9])

2)用solve(A, b)解出x，用dot()函數進行驗證，並列印

x = np.linalg.solve(A, b)
print("Solution", x)
print("Check\n", np.dot(A , x)) #用dot()函數檢查求得的解是否正確

三、特徵值和特徵向量

特徵值（eigenvalue）即方程 Ax = ax 的根，是一個標量，特徵向量是關於特徵值的向量。在numpy.linalg 模組中， eigvals函數可以計算矩陣的特徵值，而 eig 函數可以返回一個包含特徵值和對應的特徵向量的元組。

用 eigvals 函數求解特徵值

用 eig 函數求解特徵值和特徵向量 ,如下程式碼：

print("Eigenvalues", np.linalg.eigvals(A))
eigenvalues, eigenvectors = np.linalg.eig(A)
print( "First tuple of eig", eigenvalues)
print(" Second tuple of eig\n", eigenvectors)

四、奇異值分解

奇異值分解，是一種因子分解運算，將一個矩陣分解為3個矩陣的乘積。奇異值分解是特徵值分解一種推廣。在 numpy.linalg 模組中的svd()函數可以對矩陣進行奇異值分解。該函數返回3個矩陣——U、Sigma和V，其中U和V是正交矩陣，Sigma包含輸入矩陣的奇異值（計算出來結果可能是虛數）。

U, Sigma, V = np.linalg.svd(A, full_matrices=False)# 用svd() 函數分解矩陣
print ("U:",U)
print ("Sigma:",Sigma)
print ("V:", V)
print ("Product\n", U * np.diag(Sigma) * V) #用diag函數生成完整的奇異值矩陣

五、廣義

pinv 函數進行求解，計算廣義逆矩陣需要用到奇異值分解函數pinv()，行列式計算用np.linalg中的函數det()：

#使用pinv函數計算廣義逆矩陣:
A = np.mat("4 11 14;8 7 -2")
pseudoinv = np.linalg.pinv(A)
print("Pseudo inverse:\n", pseudoinv)
#計算矩陣的行列式
print("\n")
B = np.mat("3 4;5 6")
print("Determinant:", np.linalg.det(B))

全部程式碼如下：

import numpy as np
import matplotlib.pyplot as plt

A = np.mat("0 1 2;1 0 3;4 -3 8")  #用mat()函數建立範例矩陣
print ("A\n",A)
inverse = np.linalg.inv(A)  #用inv()函數計算逆矩陣
print("inverse of A\n", inverse)
print ("Check\n", A * inverse) #驗證計算，原矩陣和逆矩陣相乘的，單位矩陣
#  求解線性方程組
A = np.mat("1 -2 1;0 2 -8;-4 5 9") #用mat()函數建立範例矩陣
b = np.array([0, 8, -9])
x = np.linalg.solve(A, b)
print("Solution", x)
print("Check\n", np.dot(A , x))  #用dot()函數檢查求得的解是否正確
#特徵值和特徵向量

print("Eigenvalues", np.linalg.eigvals(A))   #eigvals函數可以計算矩陣的特徵值
eigenvalues, eigenvectors = np.linalg.eig(A) #用 eig 函數求解特徵值和特徵向量
print( "First tuple of eig", eigenvalues)
print(" Second tuple of eig\n", eigenvectors)

#奇異值分解
U, Sigma, V = np.linalg.svd(A, full_matrices=False)# 用svd() 函數分解矩陣
print ("U:",U)
print ("Sigma:",Sigma)
print ("V:", V)
print ("Product\n", U * np.diag(Sigma) * V) #用diag函數生成完整的奇異值矩陣
#使用pinv函數計算廣義逆矩陣:
A = np.mat("4 11 14;8 7 -2")
pseudoinv = np.linalg.pinv(A)
print("Pseudo inverse:\n", pseudoinv)
#計算矩陣的行列式
print("\n")
B = np.mat("3 4;5 6")
print("Determinant:", np.linalg.det(B))

執行結果：

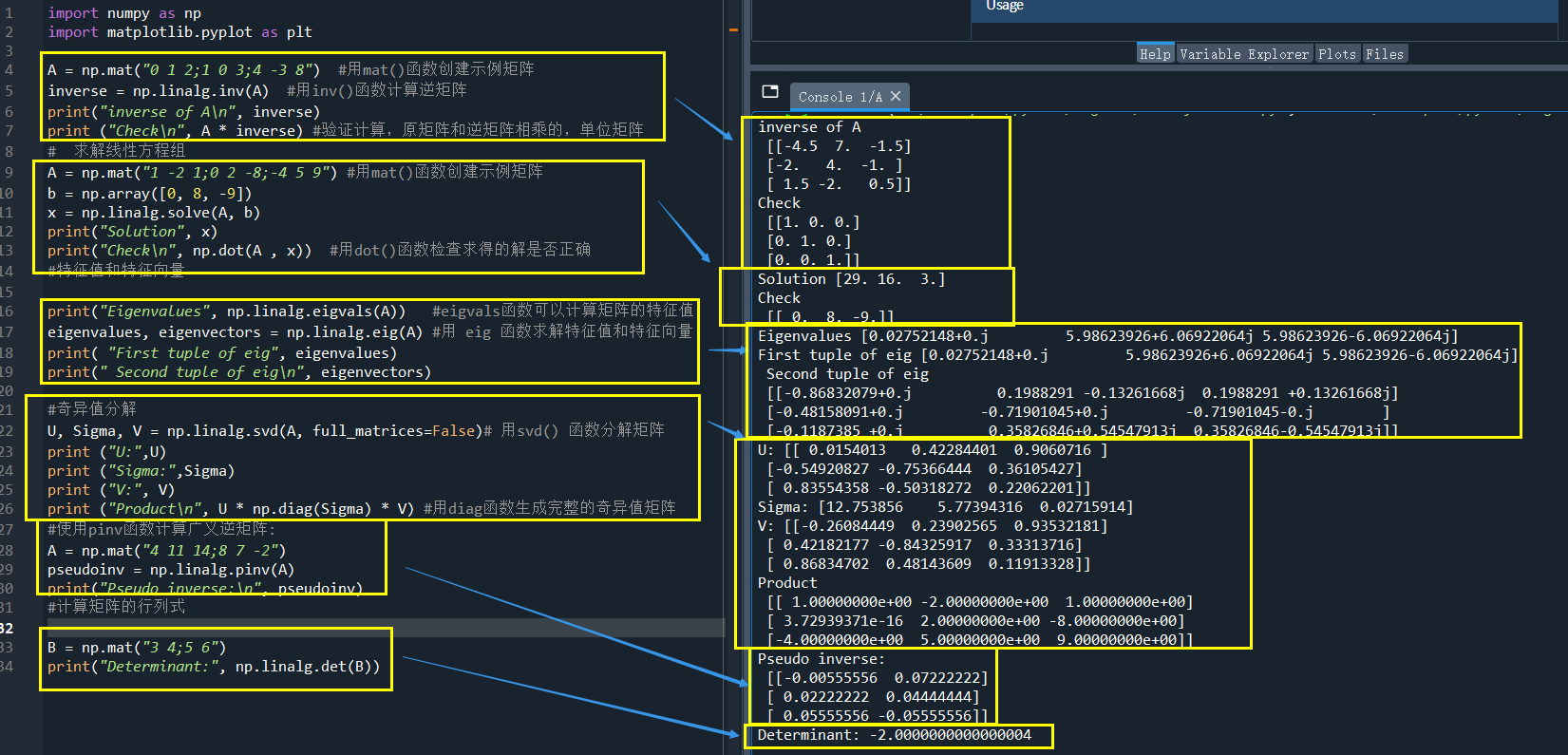
本篇介紹了一些numpy.linalg 模組中常用的函數，