技術文章 » 論文解讀（GSAT）《Interpretable and Generalizable Graph Learning via Stochastic Attention Mechanism》

論文解讀（GSAT）《Interpretable and Generalizable Graph Learning via Stochastic Attention Mechanism》

2022-08-02 06:01:32

論文資訊

論文標題：Interpretable and Generalizable Graph Learning via Stochastic Attention Mechanism
論文作者：Siqi Miao, Mia Liu, Pan Li
論文來源：2022,ICML
論文地址：download 
論文程式碼：download 

1 Introduction

1.1 引入

　　GNN的可解釋性問題：通常旨在從原始的輸入圖中提取一個子圖：人們希望提取的子圖中僅包含最能幫助標籤預測的資訊。

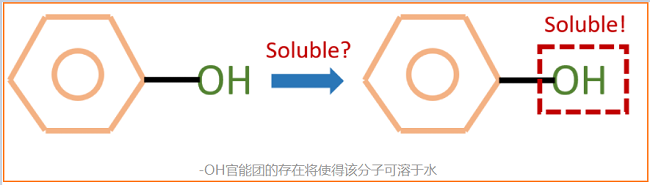
 　　例子：如下圖，我們知道-OH官能團能夠使得一個分子具有水溶性。因此對於一個用來預測分子水溶性的GNN來說，人們希望給定下圖的分子後，模型能夠告訴我們對預測最重要的部分是-OH官能團所代表的子圖。這樣一來，人們就能從模型中獲取更多的關於資料關鍵特徵的理解，從而指導進一步的研究。​

　　

　　GNN可解釋性主要有兩大類方法：

  1. 固有的可解釋模型（Inherently Interpretable Models）；
  2. 事後解釋方法（Post-hoc Interpretation Methods）；

　　第一類方法主要旨在設計自身即可提供解釋性的GNN模型。這些模型的良好可解釋性往往以其預測精度為代價，如注意力機制，多篇研究顯示其無法為GNN帶來值得信任的可解釋結果；

　　第二類方法，這些工作通常假設人們會提供一個預先訓練好的GNN。隨後它們會將該GNN的引數固定，然後訓練一個新的模型，即直譯器（Explainer），來從輸入圖中找出一個子圖。它們希望這些子圖能夠：1）儘可能小；2）儘可能保持原有預測分數。最後這些子圖即被認為是GNN捕捉到的資料的關鍵特徵。

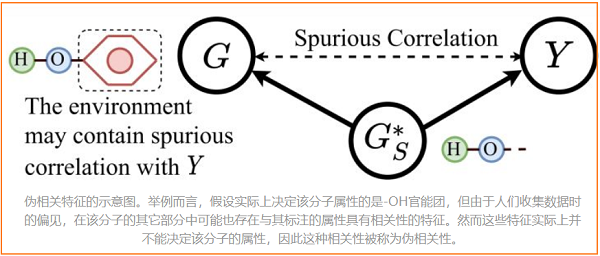
　　最近，基於不變因果特徵學習（Invariant Learning）的工作也逐漸被提出。這些工作認為訓練資料中可能會存在資料偏見（Data Bias），使得模型最終學習到一些和標籤具有偽相關性（Spurious Correlations）的特徵，並因此遭受嚴重的泛化問題。下圖展示了偽相關特徵的一個例子。這些特徵可能是收集或生成訓練資料時的偏見造成的，它們實質上並不是真正決定樣本類別的特徵。而當測試集不存在這些偽相關的特徵時，模型的效果將大打折扣。因此，這些工作引入了因果分析理論（Causality Analysis），希望迫使模型學習資料中不變的、與標籤具有因果關係的特徵（Invariant Causal Patterns），來解決上述 OOD 泛化問題（Out-of-distribution Generalization）。這類方法在尋找那些不變的因果特徵時，也能提供一定程度的自身可解釋性。不過也由於這些方法引入了因果分析，它們的架構往往十分複雜且需要大量的計算。

　　

　　而在這篇工作中，作者們指出了事後解釋方法的諸多問題，並同樣專注於設計自身可解釋模型。這篇工作提出了一種全新的隨機注意力機制（Stochastic Attention Mechanism），該機制顯示出了強大的可解釋能力和泛化能力。對比過去的可解釋工作，該機制在6個資料集上提升了至多20%、平均12%的可解釋效能；在11個資料集上提升了平均3%的模型準確率，並且在OGBG-MolHiv榜單上達到SOTA（在不使用手工設計的專家特徵的模型中）。

　　除此之外，該機制對可解釋能力和泛化能力的提升同樣具有理論保障。在一定假設下，該機制天然的不受偽相關特徵的影響，從而能夠抓取出真正重要的資料特徵。在去除偽相關特徵的能力上，該機制以遠遠更小的複雜度，對比基於因果分析的方法提升了平均12%的OOD泛化能力。

1.2 事後解釋方法的問題

　　作者們在文中首先指出了事後可解釋方法的四個問題，並認為這些事後解釋方法擅長於檢查預先訓練好的模型對一些特徵的敏感程度，但它們並不能提取出對預測真正重要的資料特徵，而這才應該是可解釋方法需要解決的最有趣的問題。具體來說，作者們指出的四個問題是：

1. 資料分佈偏移（Data Distribution Shifts）

　　首先，事後解釋方法將不可避免的遭受資料分佈偏移的影響。直覺上，這是因為給定的預先訓練好的模型（記作），總是在原始輸入圖上進行訓練的：它從來沒有在任何子圖上進行過訓練。因而極有可能在上是欠擬合的，故而導致並不能真正反應各個子圖的重要性。

2. 與標籤偽相關的資料特徵（Spuriously Correlated Patterns）

　　其次，預先訓練得到的模型可能會過擬合訓練資料中與標籤資訊偽相關，甚至是無關的特徵。這是由於大多數模型本身是基於最大化互資訊法則（Maximum Mutual Information Principle）來進行訓練的，因此在訓練中自然會捕捉儘可能多的輸入特徵，而這也是不變因果特徵學習這個方向產生的主要動機。

　　在這種情況下，事後解釋方法很可能會將這些偽相關或者無關的特徵提取出來，當作資料中的關鍵特徵，而這可能會將人們引入到一個錯誤的方向。【自編碼器預訓練 接 線性分類器.....】

3. 初始化問題（Initialization Issuses）

　　隨後，作者們從優化和資訊瓶頸理論切入，指出事後解釋方法對不同的的初始化是敏感的。在同一個資料集上，基於不同的隨機種子訓練得到的，事後解釋方法可能會得出差異較大解釋結果。而過去的事後解釋方法，在評估時往往會忽略這一點，只基於某一個固定的，僅在不同的隨機種子上訓練直譯器。這可能會得到過於樂觀的結果，而使得事後解釋方法的效能沒有得到全面的評估。【使用不同隨機種子訓練的，我就看到一個論文這樣用......】

4. 潛在的有偏見的約束（Potentially Biased Constraints）

　　最後，由於上述各種問題，事後解釋方法有時很難得出符合人們直覺的解釋子圖。故這些方法中往往嵌入稀疏化約束（Sparsity Constraint），或連線性約束（Connectivity Constraint）等，來得到人們更能理解的資料特徵。這些約束極大的要求人們對資料集和任務自身具有一定的先驗知識，否則這些約束很可能極大的影響模型的解釋結果。一個優秀的可解釋模型應當自身即能夠抓取適當的資料關鍵特徵而不用附加其它約束。本文提出的隨機注意力機制能夠在沒有上述約束的情況下，取得遠遠更好的可解釋效能。【圖結構學習吧，很重要的一點就是加圖正則化.......】

1.3 Preliminaries

Label-relevant Subgraph

　　指：子圖和圖示籤相關。如：為確定分子的溶解度，羥基-OH 是一個正相關的子圖，就好像它存在，分子通常溶於水。尋找與標籤相關的子圖是可解釋圖學習的一個共同目標。

Attention Mechanism

　　具有注意力的 GNN 經常會產生低保真度的注意力權重，因為它為每條邊學習多個權值，因此將這些權值與不規則的圖結構結合起來，進行與圖示籤相關的特徵選擇是有問題的。

　　兩種型別的注意力模型：

    • 注意力權重歸一化，求和為 1 ，如 GAT；
    • 在沒有歸一化的情況下學習 $[0,1]$ 之間的權重，如 GGNN；

Learning to Explain (L2X)

　　L2X [ 2018 ] 研究了正則特徵空間中的特徵選擇問題，並提出了一種互資訊(MI)最大化規則來選擇固定數量的特徵。

　　具體來說，讓 $I(a ; b) \triangleq \sum\limits _{a, b} \mathbb{P}(a, b) \log \frac{\mathbb{P}(a, b)}{\mathbb{P}(a) \mathbb{P}(b)}$  表示兩個隨機變數 $a$ 和 $b$ 之間的 MI。較大的 MI 表明兩個隨機變數之間存在一定的高相關性。因此，根據輸入特徵 $X \in \mathbb{R}^{F}$，L2X 是搜尋一組大小為 $k$  的索引 $S \subseteq\{1,2, \ldots, F\}$，其中 $k=|S|<F$。使由索引 $S$ (用 $X_{S}$ 表示) 的子空間中的特徵與標籤 $Y$ 的互資訊最大化，即，

　　　　$\underset{S \subseteq\{1,2, \ldots, F\}}{\text{max}}I\left(X_{S} ; Y\right), \quad \text { s.t. }|S| \leq k .\quad\quad\quad(1)$

　　本文模型的靈感來自於 L2X ，由於 圖特徵 及 可解釋的特徵 並沒有固定的維數，所以不能直接應用 L2X ，因此，本文建議使用 Sec 3.1 中使用資訊約束。

　　熵定義為 ：$H(a)   \triangleq-\sum\limits _{a} \mathbb{P}(a) \log \mathbb{P}(a)$

　　KL 散度定義為： $\mathrm{KL}(\mathbb{P}(a) \| \mathbb{Q}(a)) \triangleq \sum\limits _{a} \mathbb{P}(a) \log \frac{\mathbb{P}(a)}{\mathbb{Q}(a)}$ 

　　資訊瓶頸 IB ：$\underset{Z}{\text{max }} \mathcal{L}_{I B}=I(Z ; Y)-\beta I(X ; Z)$

3 Graph Learning Interpretation via GIB

3.1 GIB-based Objective for Interpretation

　　關鍵子圖可能具有不用的大小，以及高度不規則，所以本文建議使用資訊約束來選擇與標籤相關的子圖：

　　　　$\begin{array}{l}\underset{G_{S}}{\text{max}} &  \quad I\left(G_{S} ; Y\right) \\\text {s.t. }&  \quad I\left(G_{S} ; G\right) \leq \gamma,\quad G_{S} \in \mathbb{G}_{s u b}(G)\end{array}\quad\quad\quad(2)$

　　其中 $\mathbb{G}_{s u b}(G)$ 表示 $G$ 的子圖的集合。

　　注意，GIB 不施加任何潛在的偏差約束，如所選子圖的大小或連通性。相反，GIB 使用資訊約束 $I\left(G_{S} ; G\right) \leq \gamma$ 來選擇只從 $G$ 中繼承了最具指示性的資訊的 $G_{S}$，通過最大化 $I\left(G_{S} ; Y\right)$ 來預測標籤 $Y$。因此，GS提供了模型解釋。

3.2 Issues of Post-hoc GNN Interpretation Methods

　　幾乎所有之前的方法都是事後方法，如 GNNExplainer [2019 ]，PGExplainer [2020] 和 GraphMask [2021 ]。給定一個預先訓練的預測器 $f_{\theta}(\cdot): \mathcal{G} \rightarrow \mathcal{Y}$，他們試圖找出影響模型預測最大的子圖 $G_{S}$，同時保持預先訓練的模型不變。這個過程首先最大化了 $f_{\theta}(G)$ 和 $Y$ 之間的 MI，並得到模型引數：

　　　　$\tilde{\theta} \triangleq \arg \underset{\theta}{\text{max }} I\left(f_{\theta}(G) ; Y\right)\quad\quad\quad(3)$

　　然後優化子圖提取器 $g_{\phi}$ ：

　　　　$\begin{array}{l}\tilde{\phi} \triangleq \arg   \underset {\phi}{\text{max }}  I\left(f_{\tilde{\theta}}\left(G_{S}\right) ; Y\right) \\\text {s.t. } G_{S}=g_{\phi}(G) \in \Omega \text {. }\end{array}\quad\quad\quad(4)$

　　其中，$\Omega$ 表示滿足一些約束的子圖子集$\mathbb{G}_{s u b}(G)$。例如，GNNExcrener 和 PGExplainer 採用的基數約束。讓我們暫時忽略不同約束之間的差異，只關注優化目標。

　　事後方法的目標函數 $\text{Eq.4}$ 和 GIB（$\text{Eq.2}$）有些類似。然而，事後方法可能不能給出，甚至不能近似於 $\text{Eq.2}$ 的最優解，因為 $f_{\theta} \circ g_{\phi}$ 並不是經過聯合訓練的。從優化的角度來看，事後方法只從無約束空間的模型 $f_{\tilde{\theta}}$ 到資訊約束空間 $\Omega$ 的單步投影到 $f_{\tilde{\theta}} \circ g_{\tilde{\phi}} $（見 Fig. 4），投影規則遵循誘導的 MI 降低最小化 $I\left(f_{\tilde{\theta}}(G) ; Y\right)-I\left(f_{\tilde{\theta}}\left(g_{\tilde{\phi}}(G)\right) ; Y\right)$ 的 。

　　

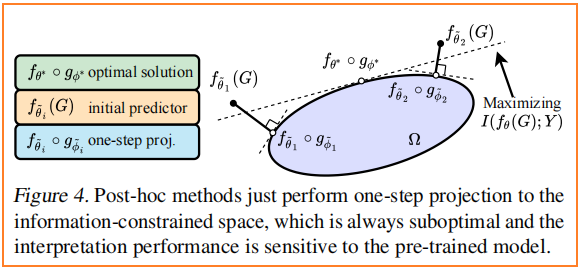
　　後果：

  • 首先，$f_{\tilde{\theta}}$ 可能不能完全從 $G_{S}=g_{\phi}(G)$ 中提取資訊來預測 $Y$，因為 $f_{\tilde{\theta}}$ 最初被訓練使 $I\left(f_{\tilde{\theta}}(G) ; Y\right)$ 近似 $I(G, Y)$ ，而 $\left(G_{S}, Y\right)=\left(g_{\phi}(G), Y\right)$ 遵循不同的 $(G, Y)$ 的分佈。因此，$I\left(f_{\tilde{\theta}}\left(G_{S}\right) ; Y\right)$ 可能不能很好地近似 $I\left(G_{S} ; Y\right)$，從而可能誤導 $g_{\phi}$ 的優化，並使 $g_{\phi}$ 不能選擇真實表示 $Y$ 的 $G_{S}$。 　　
  • 其次，對 $g_{\phi}$ 的積極優化可能會給出一個大的 MI ：$\hat{I}\left(f_{\tilde{\theta}}\left(g_{\phi}(G)\right) ; Y\right)$ （或者 相當小的訓練損失）通過選擇有助於區分訓練標籤的特徵，但本質上與標籤無關或與總體水平上的標籤虛假相關。即：無用的特徵有時也能很好的區分圖示籤。根據經驗，我們確實觀察到 Mutag 上的過擬合問題，如 Fig.5 所示，特別是 PGExplainer 和 GraphMask。在前 5 到 10 個epoch，這兩種模型成功地選擇了良好的解釋，同時有很大的訓練損失。進一步的訓練成功地減少了損失（在 10 個 epoch 之後），但卻大大降低了解釋效能。這也可能是為什麼在這些事後方法的原始文獻中，只建議在少數epoch上進行訓練的原因。然而，在實際任務中，很難有地面真實解釋標籤來驗證結果，並確定一個可靠的停止標準。

　　

　　事後方法存在初始化問題。它們的可解釋性對預先訓練好的模型$f_{\tilde{\theta}}$ 高度敏感，Fig.5 中的大方差證明了這一點。只有當預訓練的 $f_{\tilde{\theta}}$ 近似於最優 $f_{\theta^{*}}$ 時，才能大致保證其效能。因此，根據 GIB 原理等式對 $f_{\theta} \circ g_{\phi}$ 進行聯合訓練通常需要根據 $\text{Eq.}$ 的 GIB 準則。

4 Stochastic Attention Mechanism for GIB

　　在本節中，首先給出 GIB 目標的變分界（$\text{Eq.2}$），然後引入帶有隨機注意機制的模型GSAT。

4.1 A Tractable Objective for GIB

　　GSAT 是學習一個引數 $\phi$ 的子圖提取器來提取 $G_{S} \in \mathbb{G}_{\text {sub }}(G)$。$g_{\phi}$ 通過注入的隨機性阻斷資料 $G$ 中與標籤無關的資訊，同時允許 $G_{S}$ 中儲存的與標籤相關的資訊做出預測。

　　在 GSAT中，$g_{\phi}(G)$ 本質是 $\mathbb{G}_{\text {sub }}(G)$ 上的分佈，將該分佈表示為 $\mathbb{P}_{\phi}\left(G_{S} \mid G\right)$。$g_{\phi}(G)$ 即為 $\mathbb{P}_{\phi}\left(G_{S} \mid G\right)$ 。

　　對於一些 $\beta>0$，通過 GIB 得到了 $g_{\phi}$ 的優化：

　　　　$\underset{\phi}{\text{min}} -I\left(G_{S} ; Y\right)+\beta I\left(G_{S} ; G\right) \text {, s.t. } G_{S} \sim g_{\phi}(G) \quad\quad\quad(5)$

　　接下來，我們推匯出 $\text{Eq.5}$ 中這兩項的一個可處理的變分上界。詳細的推導在附錄 B 中給出。

　　對於項 $I\left(G_{S} ; Y\right)$，引入針對 $\mathbb{P}\left(Y \mid G_{S}\right)$ 的引數化變分近似 $\mathbb{P}_{\theta}\left(Y \mid G_{S}\right)$，得到一個下界：

　　　　$I\left(G_{S} ; Y\right) \geq \mathbb{E}_{G_{S}, Y}\left[\log \mathbb{P}_{\theta}\left(Y \mid G_{S}\right)\right]+H(Y)\quad\quad\quad(6)$

　　在本文模型，$\mathbb{P}_{\theta}\left(Y \mid G_{S}\right)$ 本質上可以作為引數 $\theta$ 的預測器 $f_{\theta}: \mathcal{G} \rightarrow \mathcal{Y}$。

　　對於項 $I\left(G_{S} ; G\right)$，引入邊際分佈 $\mathbb{P}\left(G_{S}\right)=   \sum_{G} \mathbb{P}_{\phi}\left(G_{S} \mid G\right) \mathbb{P}_{\mathcal{G}}(G)$ 的變分近似 $\mathbb{Q}(G_{S})$。並得到上界：

　　　　$I\left(G_{s} ; G\right) \leq \mathbb{E}_{G}\left[\operatorname{KL}\left(\mathbb{P}_{\phi}\left(G_{S} \mid G\right) \| \mathbb{Q}\left(G_{S}\right)\right)\right]\quad\quad\quad(7)$

　　插入上述兩個不等式，得到了 $\text{Eq.5}$ 的一個變分上界作為 GSAT 的目標：

　　　　$\begin{array}{l}  \underset{\theta, \phi}{\text{min}}   -\mathbb{E}\left[\log \mathbb{P}_{\theta}\left(Y \mid G_{S}\right)\right]+\beta \mathbb{E}\left[\operatorname{KL}\left(\mathbb{P}_{\phi}\left(G_{S} \mid G\right) \| \mathbb{Q}\left(G_{S}\right)\right)\right] \\\text { s.t. } \quad G_{S} \sim \mathbb{P}_{\phi}\left(G_{S} \mid G\right)\end{array}\quad\quad\quad(8)$

　　接下來，在 GSAT 中指定 $\mathbb{P}_{\theta}$（又名 $f_{\theta}$）、$\mathbb{P}_{\phi}$（又名 $g_{\phi}$）和 $Q$。

4.2 GSAT and Stochastic Attention Mechanism

Stochastic Attention via $\mathbb{P}_{\phi}$

　　提取器 $g_{\phi}$ 首先通過GNN將輸入圖 $G$ 編碼為一組節點表示形式 $\left\{h_{v} \mid v \in V\right\}$。對於每條邊 $(u, v) \in E$ ，$g_{\phi}$ 包含一個 MLP 層後接 $sigmoid$，它將邊連線 $\left(h_{u}, h_{v}\right)$ 對映到 $p_{u v} \in[0,1]$。然後，對於訓練的每一次向前傳遞，從伯努利分佈 $\alpha_{u v} \sim \operatorname{Bern}\left(p_{u v}\right)$ 中抽取隨機注意。為確保梯度 $p_{u v}$ 是可計算的，應用 gumbel-softmax 重新引數化技巧。提取的圖 $G_{S}$ 將有一個被注意選擇的子圖為 $A_{S}=\alpha \odot A$。這裡 $\alpha$ 是 $(u, v) \in E$ 項為 $\alpha_{u v}$ 的矩陣，或者非邊項為零。上述程式給出 $G$ 的 $G_{S}$ 的分佈，描述了 $\mathbb{P}_{\phi}\left(G_{S} \mid G\right) $，所以 $\mathbb{P}_{\phi}\left(G_{S} \mid G\right)=\prod\limits _{u, v \in E} \mathbb{P}\left(\alpha_{u v} \mid p_{u v}\right)$，其中 $p_{u v}$ 是 $G$ 的一個函數，這本質上使得注意 $\alpha_{u v}$ 在給定輸入圖 $G$ 的不同邊上是有條件地獨立的。

Prediction via $\mathbb{P}_{\theta}$

　　預測器 $f_{\theta}$ 採用相同的 GNN 將提取的圖 $G_{S}$ 編碼為圖表示，最後將該表示通過 MLP 層加 softmax 對 $Y$ 的分佈進行建模。該過程給出了變分分佈 $\mathbb{P}_{\theta}\left(Y \mid G_{S}\right)$。

Marginal Distribution Control via $\mathbb{Q}$

　　$\text{Eq.7}$ 對於任何 $\mathbb{Q}\left(G_{S}\right)$ 都總是正確的。我們對 $\mathbb{Q}\left(G_{S}\right)$ 的定義如下。

　　對於 $G$ 中的每個圖 $G \sim \mathbb{P}_{\mathcal{G}}$ 和 $G$ 中的每兩個有向節點對 $(u, v)$，我們取樣 $\alpha_{u v}^{\prime} \sim \operatorname{Bern}(r)$，其中 $r \in[0,1]$ 是一個超引數。如果 $\alpha_{u v}^{\prime}=1$，我們刪除 $G$ 中的所有邊，並新增所有邊 $(u，v)$。假設得到的圖為 $G_{S}$。此過程定義了分佈 $\mathbb{Q}\left(G_{S}\right)= \sum_{G} \mathbb{P}\left(\alpha^{\prime} \mid G\right) \mathbb{P}_{\mathcal{G}}(G)$ 。由於 $\alpha^{\prime}$ 獨立於圖 $G$，假設其大小為 $n$，$\mathbb{Q}\left(G_{S}\right)=\sum_{n} \mathbb{P}\left(\alpha^{\prime} \mid n\right) \mathbb{P}_{\mathcal{G}}(G=n)= \mathbb{P}(n) \prod_{u, v=1}^{n} \mathbb{P}\left(\alpha_{u v}^{\prime}\right)$。一個大小為 $n$ 的圖的概率 $\mathbb{P}(n)$ 是一個常數，因此不會影響模型。請注意，我們對 $\mathbb{Q}\left(G_{S}\right)$ 的選擇具有使用標準高斯分佈作為變分自動編碼器的潛在分佈的相似精神。

　　使用上面的 $\mathbb{P}_{\theta}$，$\text{Eq.8}$ 中的第一項減少為一個標準的交叉熵損失。使用 $\mathbb{P}_{\phi}$ 和 $\mathbb{Q}$ ，對於每一個 $G \sim \mathbb{P}_{\mathcal{G}}$，$n$ 為 $G$ 的大小，kl-散度項變為

　　　　$\begin{array}{l}\mathrm{KL}\left(\mathbb{P}_{\phi}\left(G_{S} \mid G\right) \| \mathbb{Q}\left(G_{S}\right)\right)= \\\sum\limits_{(u, v) \in E} p_{u v} \log \frac{p_{u v}}{r}+\left(1-p_{u v}\right) \log \frac{1-p_{u v}}{1-r}+c(n, r)\end{array}\quad\quad\quad(9)$

　　其中 $c(n，r)$ 是一個沒有任何可訓練引數的常數。

4.3 The Interpretation Mechanism of GSAT

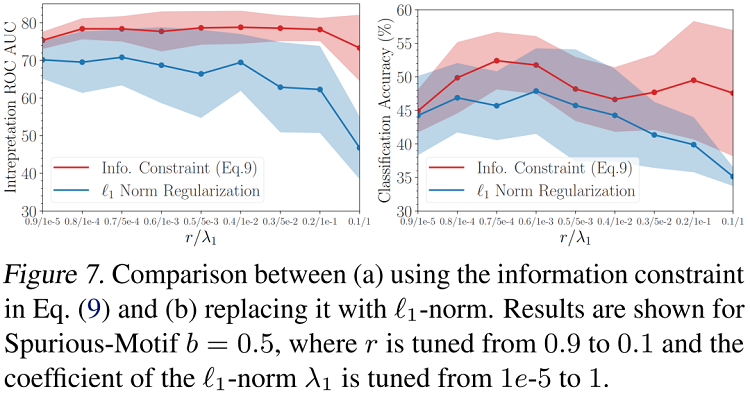
　　GSAT 的可解釋性本質上來自於資訊控制：GSAT通過注意向 $G_{S}$ 中注入隨機性來減少輸入圖中的資訊。在訓練中，$\text{Eq.9}$ 中的正則項將嘗試為所有邊緣分配較大的隨機性，但在分類損失 $\min -I\left(G_{S} ; Y\right)$（相當於交叉熵損失）的驅動下，GSAT 可以學習減少在任務相關子圖上的注意力的隨機性。因此，提供模型解釋的不是整個 $G_{S}$，而是具有隨機減少注意力的部分，又名 $p_{u v} \rightarrow 1$。因此，當 GSAT 提供解釋時，在實踐中，我們可以根據 $p_{u v}$ 對所有的邊進行排序，並使用那些排名靠前的邊（如果需要，給定一定的預算）作為檢測到的子圖進行解釋。正如實驗中（Table 5）所示的那樣，注入隨機性對效能的貢獻非常顯著，而我們的正則化項的貢獻( $\text{Eq.9}$ )，當我們將其與稀疏性驅動的 $\ell_{1}-\text { norm }$ 進行比較時（Fig. 7）。

　　GSAT與以前的方法有本質的不同，因為我們沒有使用任何稀疏性約束，如 $\ell_{1}-\text { norm }$ ，$\ell_{0}-\text { norm }$或 $\ell_{2}-\text { norm-regression}$ 到 {0,1}來選擇大小約束（或連通性約束）子圖。我們實際上觀察到，在邊緣正則化( $\text{Eq.9}$ )中，設定 $r$ 遠離 $0$ ，也就是說，使 $G_{S}$ 遠離稀疏，通常會提供更穩健的解釋。這與我們的直覺相吻合，即GIB根據定義並不對選定的子圖做出任何假設，而只是限制了來自原始圖的資訊。我們的實驗表明，即使在優化過程中沒有利用這些假設，GSAT也顯著優於基線，即使與標籤相關的子圖滿足這些假設。如果與標籤相關的子圖確實斷開或大小變化，GSAT的改進預計會更大。

4.4. Further Comparison on Interpretation Mechanism

　　PGExcwaner 和 GraphMask 在他們的模型中也具有隨機性。然而，他們的主要目標是在一個離散的子圖選擇空間上實現基於梯度的搜尋，而不是像 GSAT 那樣控制資訊。因此，他們在原則上並沒有像我們的那樣得出資訊正則化( $\text{Eq.9}$ )，但採用稀疏性約束來提取一個直接用於解釋的小子圖 $G_{S}$。

　　IB-subgraph 考慮使用 GIB 作為目標，但不注入任何隨機性來生成 $G_{S}$，因此其選擇的子圖 $G_{S}$ 是 $G$ 的確定性函數。具體來說，IB-subgraph 取樣圖 $G$ 來估計 $I(GS；G)$ 並優化確定性函數 $G_{S}=g_{\phi}(G)$ 以最小化這種MI估計。在這種情況下，$I\left(G_{S} ; G\right)\left(=H\left(G_{S}\right)-H\left(G_{S} \mid G\right)\right)$ 簡化為熵 $H\left(G_{S}\right)$，這傾向於給出一個小尺寸的 $G_{S}$，因為小圖的空間很小，並且有一個熵的下上界。相比之下，$G_{S} \sim g_{\phi}(G)$ 在GSAT中是隨機的，而 GSAT 主要通過注入隨機性來增加 $H\left(G_{S} \mid G\right)$ 來實現GIB。

4.5 Guaranteed Spurious Correlation Removal

　　GSAT可以消除訓練資料中的虛假相關性，並保證了可解釋性。我們可以證明，如果子圖模式 $G_{S}^{*}$ 與標籤 $Y$ 之間存在對應關係，則模式 $G_{S}^{*}$ 是 GIB 目標的最優解( $Eq.2$)。

　　Theorem 4.1. Suppose each $G$ contains a subgraph $G_{S}^{*}$ such that $Y$ is determined by $G_{S}^{*}$ in the sense that $Y= f\left(G_{S}^{*}\right)+\epsilon$ for some deterministic invertible function $f$ with randomness $\epsilon$ that is independent from $G$ . Then, for any $\beta \in[0,1]$, $G_{S}=G_{S}^{*}$ maximizes the GIB $I\left(G_{S} ; Y\right)- \beta I\left(G_{S} ; G\right)$ , where $G_{S} \in \mathbb{G}_{\text {sub }}(G)$ .

　　Proof. Consider the following derivation:

　　　　$\begin{aligned}& I\left(G_{S} ; Y\right)-\beta I\left(G_{S} ; G\right) \\=& I\left(Y ; G, G_{S}\right)-I\left(G ; Y \mid G_{S}\right)-\beta I\left(G_{S} ; G\right) \\=& I\left(Y ; G, G_{S}\right)-(1-\beta) I\left(G ; Y \mid G_{S}\right)-\beta I\left(G ; G_{S}, Y\right) \\=& I(Y ; G)-(1-\beta) I\left(G ; Y \mid G_{S}\right)-\beta I\left(G ; G_{S}, Y\right) \\=&(1-\beta) I(Y ; G)-(1-\beta) I\left(G ; Y \mid G_{S}\right)-\beta I\left(G ; G_{S} \mid Y\right)\end{aligned}$

　　其中第三個相等式是由於 $G_{S} \in \mathbb{G}_{s u b}(G)$，那麼 $\left(G_{S}, G\right)$ 沒有比 $G$ 持有更多的資訊。

　　如果 $\beta \in[0,1]$，$G_{S}$ 的最大化 $I\left(G_{S}, Y\right)-\beta I\left(G_{S} ; G\right)$ 也可以最小化 $(1-\beta) I\left(G ; Y \mid G_{S}\right)+\beta I\left(G ; G_{S} \mid Y\right)$，$(1-\beta) I\left(G ; Y \mid G_{S}\right)+\beta I\left(G ; G_{S} \mid Y\right)$ 的下界為 0。

　　$G_{S}^{*}$ 是生成 $(1-\beta) I\left(G ; Y \mid G_{S}^{*}\right)+   \beta I\left(G ; G_{S}^{*} \mid Y\right)=0$ 的子圖。這是因為(a) $Y=f\left(G_{S}^{*}\right)+\epsilon$，其中 $\epsilon$ 獨立於 $G$，所以 $I\left(G ; Y \mid G_{S}^{*}\right)=0$ 和 (b) $G_{S}^{*}=f^{-1}(Y-\epsilon)$，其中 $\epsilon$ 獨立於 $G$，所以 $I\left(G ; G_{S}^{*} \mid Y\right)=0$。因此，$G_{S}=G_{S}^{*}$ 最大限度地提高了GIB $I\left(G_{S} ; Y\right)-\beta I\left(G_{S} ; G\right)$，其中 $G_{S} \in \mathbb{G}_{\mathrm{sub}}(G)$。

　　雖然 $G_{S}^{*}$ 決定了 $Y$，但在訓練資料集中，資料 $G$ 和 $Y$ 可能存在一些由環境造成的虛假相關性。也就是說，$G\text{\ }G∗S$ 可能與標籤有一定的相關性，但這種相關性是虛假的，並不是決定其標籤的真正原因（如 $Fig.6$ 所示）。一個經過訓練的 $G$，通過MI最大化來預測 $Y$ 的模型可以捕捉到這種虛假的相關性。如果這種相關性在測試階段發生變化，模型就會出現效能下降。

　　然而，Theorem 4.1 表明，GSAT通過優化GIB目標，能夠僅通過提取 $G_{S}^{*}$ 來解決上述問題，從而消除了虛假的相關性，也提供了有保證的可解釋性。

4.6. Fine-tuning and Interpreting a Pre-trained Model

　　GSAT還可以微調和解釋一個預先訓練好的GNN。給定一個由 $\max _{\theta} I\left(f_{\theta}(G) ; Y\right)$ 預先訓練的 $f_{\tilde{\theta}}$，GSAT 可以通過 $\max _{\theta, \phi} I\left(f_{\theta}\left(G_{S}\right) ; Y\right)-\beta I\left(G_{S} ; G\right) $，$G_{S} \sim g_{\phi}(G)$ 進行微調，通過初始化 $g_{\phi}$ 和 $f_{\theta}$ 中使用的GNN作為預先訓練的模型 $f_{\tilde{\theta}}$。

　　我們觀察到，這個框架幾乎永遠不會損害原始的預測效能（有時甚至會提高它）。此外，與從頭開始訓練GNN相比，該框架往往能獲得更好的解釋結果。

5 Experiments

　　由上一節可見，GSAT架構簡單直接，但同時其效能又具有理論保障。這一章節將通過實驗結果具體展示GSAT的可解釋能力、泛化能力和各模組的消融實驗結果。

可解釋性

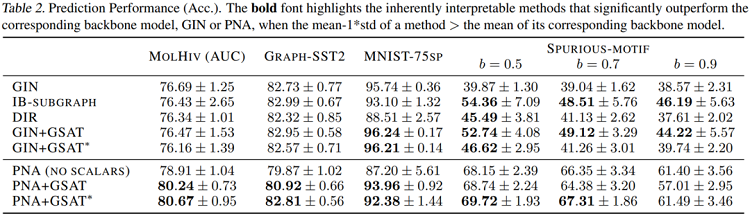
　　作者們在真實資料集和合成資料集上都對GSAT的可解釋性進行了評估。作者們基於這些資料集中已知的解釋標註對每個方法的解釋結果評估了ROC AUC。如下圖，GSAT對比過去的可解釋工作，在6個資料集上提升了至多20%、平均12%的可解釋效能。

　　

泛化效能

　　由於GSAT能夠幫助去除偽相關性，它同時也能幫助提升模型的分類泛化能力。如下圖，GSAT在11個資料集上提升了平均3%的模型準確率，並且在OGBG-MolHiv榜單上達到SOTA（在不使用手工設計的專家特徵的模型中）。

　　

OOD泛化效能（偽相關性移除）

　　為了對比GSAT的移除偽相關特徵的能力，作者們同時提供了和不變因果特徵學習的方法的直接對比。如下圖，可見GSAT能夠在不利用因果分析框架的情況下，以更為簡單的架構提升平均12%的OOD泛化能力。

　　

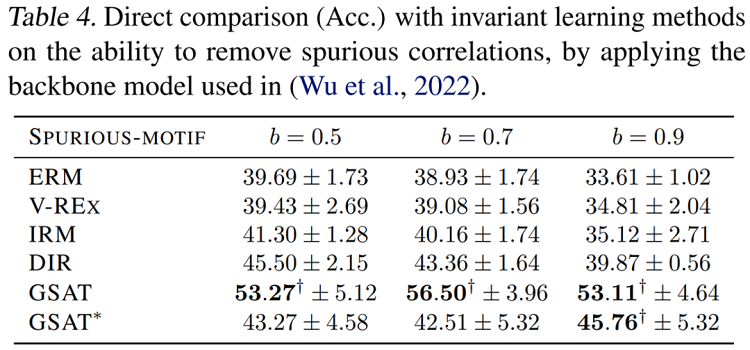
消融實驗

　　作者們提供了GSAT中各個模組的消融實驗結果，如下表，可見當不注入隨機性（NoStoch），或者不新增正則項（$\beta=0$）時，模型效果均會大幅下降。而當不注入隨機性時，模型效果將遭受最大的下降。這一消融實驗展示了注入的隨機性在GSAT中扮演著極其重要的角色。

　　

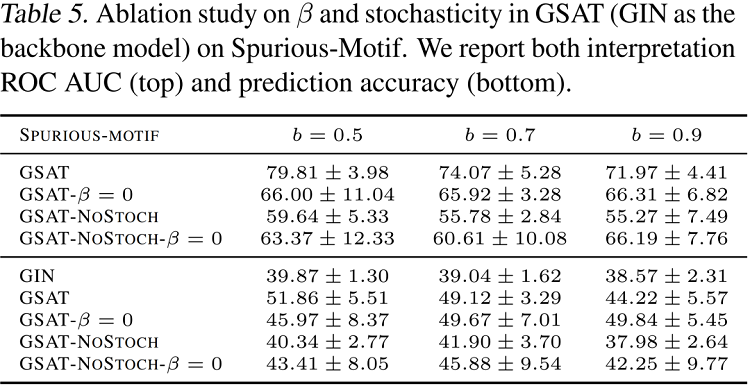
　　作者們同樣實驗了將從資訊瓶頸中推導得來的KL散度正則項替換成過去的方法常用的 $\ell_{1}$ 正則。下圖對各正則項的係數進行了網格搜尋，可見文中提出的資訊正則項顯著優於$\ell_{1}$正則。 

　　

6 Conclusion

　　圖隨機注意(GSAT)是一種建立可解釋圖學習模型的新型注意機制。GSAT注入了隨機性來阻斷與標籤無關的資訊，並利用減少隨機性來選擇與標籤相關的子圖。這種基本原理是基於資訊瓶頸原理建立的。GSAT具有許多具有變革性的特徵。例如，它消除了圖學習解釋中的稀疏性、連續性或其他潛在的偏差假設，而沒有效能衰減。它還可以消除偽相關，更好地提高模型泛化。作為一個副產品，我們還從資訊瓶頸的優化角度揭示了事後解釋方法背後的一個潛在的嚴重問題。

7 GSAT 簡單版

　　在很長的一段時間裡，人們認為注意力機制無法提供較好的可解釋性，尤其是在圖學習領域。而該論文的作者們提出了一種隨機注意力機制，並特別的在圖學習領域進行了推導和評估，作者們稱該機制為GSAT，即圖隨機注意力（Graph Stochastic Attention）。後續實驗表明該機制能夠同時提供強大的可解釋能力和泛化能力。

機制原理

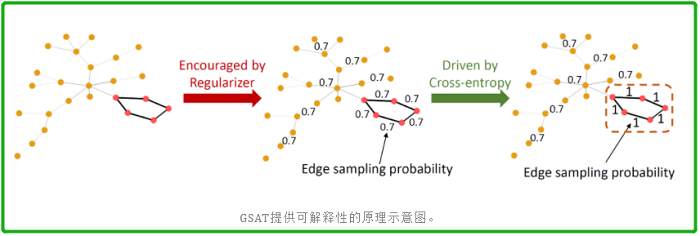
　　隨機注意力機制，顧名思義，即是在學習注意力時注入隨機性。下圖提供了其在圖學習領域的一個例子。該任務目標是預測圖中是否存在五節點環（由圖中粉色節點包圍），這些環中的邊是自然則是對預測結果重要的邊。該機制原理的直覺如下：

  1. 首先，每一條邊將會習得一個 $[0,1]$ 之間的注意力權重，該權重將指代每一條邊在訓練中的抽樣概率。一個正則項需要被引入來鼓勵每一條邊習得較小的抽樣概率，即維持較大的隨機性。如下圖中間樣本。
  2. 隨後，倘若對預測結果重要的邊存在較大的隨機性，那麼它們在訓練中將會被過於頻繁的丟棄，而這將極大的影響分類損失（交叉熵）。因此被分類損失推動，重要的邊最後則會維持較小的隨機性，即習得較大的抽樣概率（理想情況下接近於 $1$）。如下圖右側樣本。
  3. 最後，每條邊的隨機程度指代其對預測效能的重要程度，而越重要的邊應有越大的抽樣概率。如下圖右側樣本虛線框中的子圖即為低隨機性的子圖，它代表著對預測最為重要的子圖。

　　

訓練目標

　　現在的問題即是，上述的正則項應當如何選取呢？事實上這也非常直覺。因為作者們的目標是控制訓練圖中的隨機性，而從資訊理論的角度來說，作者們即是希望控制圖中的資訊量。那麼一個顯而易見的選擇就是資訊瓶頸理論（Information Bottleneck Principle）。通過注入資訊瓶頸，GSAT能夠天然的控制圖中的資訊量，從而達到預期的效果。

　　具體而言，圖資訊瓶頸損失可以寫作：

　　　　$\begin{array}{l}\underset{\theta, \phi}{\text{min}}-I\left(f_{\theta}\left(G_{S}\right), Y\right)+\beta I\left(G_{S} ; G\right) \\\text { s.t. } G_{S} \sim g_{\phi}(G)\end{array}$

　　其中  $I(. ; .)$  代表兩個隨機變數之間的互資訊量（Mutual Information）,  $\beta$ 是一個正則係數, 代表 資訊瓶頸注入的強度。  $g_{\phi}$  是一個負責從原圖  $G$  中提取子圖  $G_{S}$  的模型, 而  $f_{\theta}$  則是負責對提取出的子 圖  $G_{S}$  進行下游任務  $Y$  的預測的模型。

　　互資訊量自身不易優化，作者們為上述目標中的兩項分別推匯出了變分上界（Variational  Upper Bound）來優化該目標。

  1. 對於第一項 $-I\left(f_{\theta}\left(G_{S}\right), Y\right)$ , 易得其變分上界即為 $-\mathbb{E}\left[\log \mathbb{P}_{\theta}\left(Y \mid G_{S}\right)\right]$ , 而這事實上就是 $f_{\theta}$ 基於 $G_{S}$ 進行預測後產生的交叉熵損失。
  2. 對於第二項中的 $I\left(G_{S} ; G\right)$ , 易得其變分上界為 $\mathbb{E}\left[\operatorname{KL}\left(\mathbb{P}_{\phi}\left(G_{S} \mid G\right) \| \mathbb{Q}\left(G_{S}\right)\right)\right]$ , 其中 $\mathbb{P}_{\phi}\left(G_{S} \mid G\right)$ 即 為 $g_{\phi}$ 基於 $G$ 得到的每條邊的取樣概率; 而 $\mathbb{Q}\left(G_{S}\right)$ 即是對各邊取樣概率分佈的一個正則, 因為該 $\mathrm{KL}$ 散度本質上將鼓勵習得的每條邊的取樣分佈逼近 $\mathbb{Q}\left(G_{S}\right)$ 的分佈。舉例來說, 倘若 $\mathbb{Q}\left(G_{S}\right)$ 是 一個引數為 $0.7$ 的伯努利分佈, 那麼這一項則將鼓勵每條邊的取樣概率接近 $0.7$ , 而這正好符合 作者們對隨機注意力機制中正則項工作原理的期待。

有保障的可解釋性和OOD泛化（偽相關性去除）能力

　　由上文可知，最終GSAT的訓練目標即是一個分類損失（鼓勵高分類效能），加上一個KL散度的正則項（鼓勵高隨機性）。理想情況下，我們期待當模型僅將重要的邊維持較小的隨機性時，該訓練目標應該被最小化，因為在這種情況下我們可能可以在達到最高分類效能的同時，取得最高的整體隨機性。而作者們則在論文的定理4.1中證明了這一點，使得GSAT的效能具有理論保障。

　　具體來說，論文中定理4.1表明: 給定一個任務，如果我們假設輸入圖 $G$ 中包含一個子圖 $G_{S}^{*}$ , 並 且其標籤 $Y$ 將由下式決定: $Y=f\left(G_{S}^{*}\right)+\epsilon$ , 其中 $f$ 是一個可逆的且無隨機性的函數，$\epsilon$ 是與 $G$ 無關的隨機噪聲。那麼對於任何的 $\beta \in[0,1]$，$G_{S}=G_{S}^{*}$ 能夠最小化上文提出的資訊瓶頸損失。

　　這意味著GSAT能夠在不利用因果分析工具的情況下，天然的找出真正重要的子圖 $G_{S}^{*}$ ，並且移除可能存在的偽相關特徵，從而提供有保障的可解釋性和OOD泛化能力。

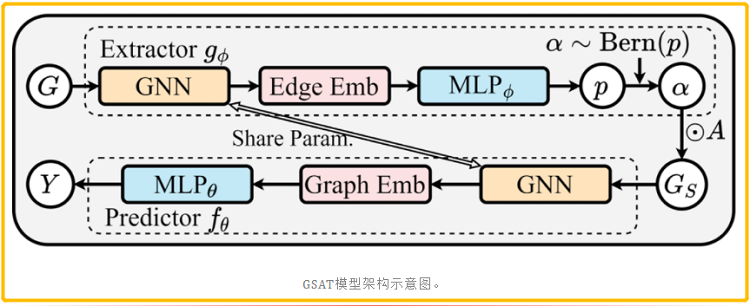
GSAT 模型架構

　　有了文中提出的兩個變分上界, 那麼GSAT的模型架構問題則變得一目瞭然。現在只需要對  $\mathbb{P}_{\theta}\left(Y \mid G_{S}\right)$  和  $\mathbb{P}_{\phi}\left(G_{S} \mid G\right)$  進行適當的引數化。

　　直覺來說，如下圖：

  1. $\mathbb{P}_{\phi}\left(G_{S} \mid G\right)$ 的輸入是原始圖 $G$ ，其對每一條邊輸出一個注意力權重，那麼 $g_{\phi}$ 顯然可以是一個這 樣工作的GNN。
  2. $\mathbb{P}_{\theta}\left(Y \mid G_{S}\right)$ 的輸入是子圖 $G_{S}$ ，其輸出對該樣本的標籤預測，那麼 $f_{\theta}$ 顯然可以是一個這樣工作的 GNN。
  3. 因此，在GSAT中， $g_{\phi}$ 將會接受原圖 $G$ 作為輸入，然後輸出每一條邊的隨機注意力的值。緊接 著，基於隨機注意力的取值，一個子圖 $G_{S}$ 將會被取樣出來。最後 $G_{S}$ 將會被餵給 $f_{\theta} $ 進行最後的 標籤預測。
  4. 儘管 $f_{\theta}$ 和 $g_{\phi}$ 可以是兩個不同的 $\mathrm{GNN}$ ，但作者們發現這裡用同一個 GNN 效果就足夠好。另外，架構中 $g_{\phi}$ 最後的取樣操作本身是不可導的，因此作者們提出利用Gumbel-softmax Trick來重 引數化這一步驟，使其可導。