技術文章 » Multi-Party Threshold Private Set Intersection with Sublinear Communication-2021:解讀

Multi-Party Threshold Private Set Intersection with Sublinear Communication-2021:解讀

2022-08-01 18:00:45

記錄閱讀論文的筆記。

摘要


總結：
（1）CRYPTO 2019:The Communication Complexity of Threshold Private Set Intersection-2019：解讀提出任何閾值PSI得通訊複雜度為\(\Omega(T)\)；基於FHE的兩方閾值PSI通訊複雜度為\(O(T)\)，但計算消耗很大麼；基於GC的了；兩方閾值PSI得通訊複雜度為\(O(T^3)\)，並給出了一個通訊複雜度為\(O(T^2)\)的基於AHE的兩方閾值PSI協定。

（2）本文和Multiparty Cardinality Testing for Threshold Private Set-2021：解讀在同一年提出，難免相似。
（3）在本文中，研究多方閾值PSI的通訊複雜度，分為兩個功能：
第一，參與方檢測資料集與交集的最大相差是否為\(T\)？
即對於\(I=S_{\cap}\)，判斷\(|S_i \setminus I|\leq T\)，或\(|I|\geq m-T\)是否成立？（\(m\)是資料集大小）
關注的是交集（相同資料的個數）是否足夠大！，記做\(F_{TPSI-int}\)。

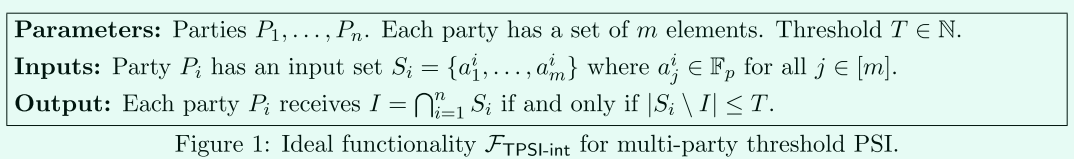
第二，參與方檢測並集與交集的最大相差是否為\(T\)？
即判斷\(|\bigcup_{i=1}^{n}S_i\setminus I|\leq T\)是否成立？
關注的是差集（不同資料的個數）是否足夠小！記做\(F_{TPSI-diff}\)

這兩個功能在兩方下是等效的，在多方下不是。
因為在兩方中，要求\(|\bigcup_{i=1}^{n}S_i\setminus I|=2|S_i\setminus I|\)，所以不用區分。在多方中，我們知道\(2|S_i\setminus I|\leq |\bigcup_{i=1}^{n}S_i\setminus I|\leq n.|S_i\setminus I|\)，因此和兩方的不同！

（4）本文中，給出任何協定的通訊複雜度為\(\Omega(nT)\)；在閾值FHE下的協定最大通訊複雜度為\(O(nT)\)，本文設計的協定的通訊複雜度只依賴於（only資料），而不依賴集合的輸入。
（5）在本文中，給出以上兩個功能函數的通訊複雜度的上限和下限。

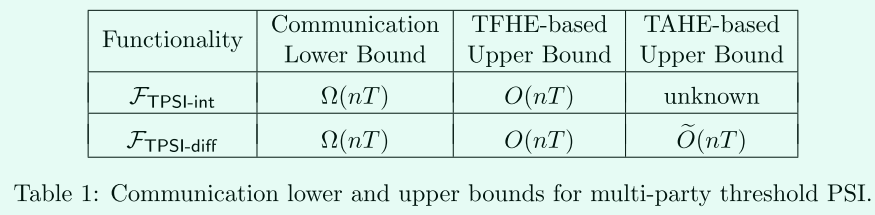
其中TFHE是全同態加密方案，TAHE是加法同態性的加密方案；安全性是半誠實的。
下面是對通訊複雜度的上限分析，閾值PSI一般分為兩個階段：
第一階段：

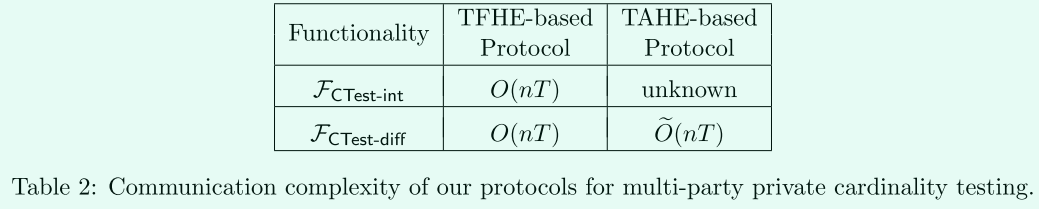
主要就是進行cardinality testing，判斷交集是否足夠大，詳細點說可以分為兩種：
對於\(F_{TPSI-int}\)，即判斷\(|I|\geq m-T\)是否成立？，記做\(F_{CTest-diff}\)。

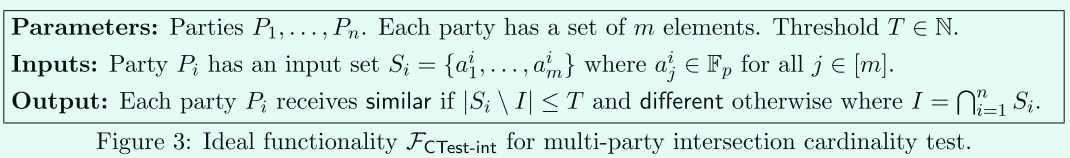
對於\(F_{TPSI-diff}\)，即判斷\(|\bigcup_{i=1}^{n}S_i\setminus I|\leq T\)是否成立？，記做\(F_{CTest-diff}\)。

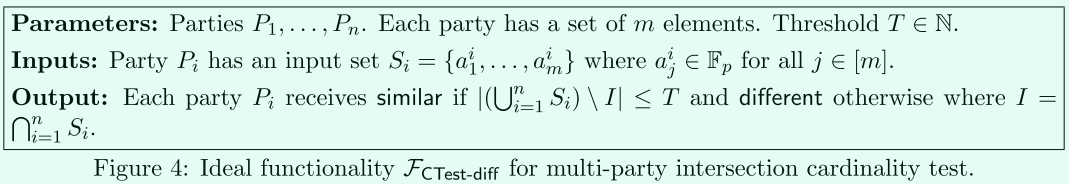
第二階段：
如果交集足夠大，即通過了cardinality testing，就會進入第二階段，各方找到他們的差集\(S_i\setminus I\)。
該階段只使用TAHE，通訊複雜度為\(O(nT)\)，再結合第一階段（表2）就會得到最終的通訊複雜度（表1）。

介紹


1、PSI的應用：
（1）DNA測試和圖形識別
（2）遠端診斷
（3）殭屍網路檢測
（4）線上廣告
2、PSI模式：
（1）兩方
（2）多方
（3）雲輔助
3、PSI安全模型：
（1）半誠實
（2）惡意

設計結構

這裡也是多方參與的協定，使用的是星型拓撲結構（star network），即一個leader方（designated party）和其他方互動，該結構的優點就是，無需所有方都同時線上。用於分析通訊複雜度上限時。

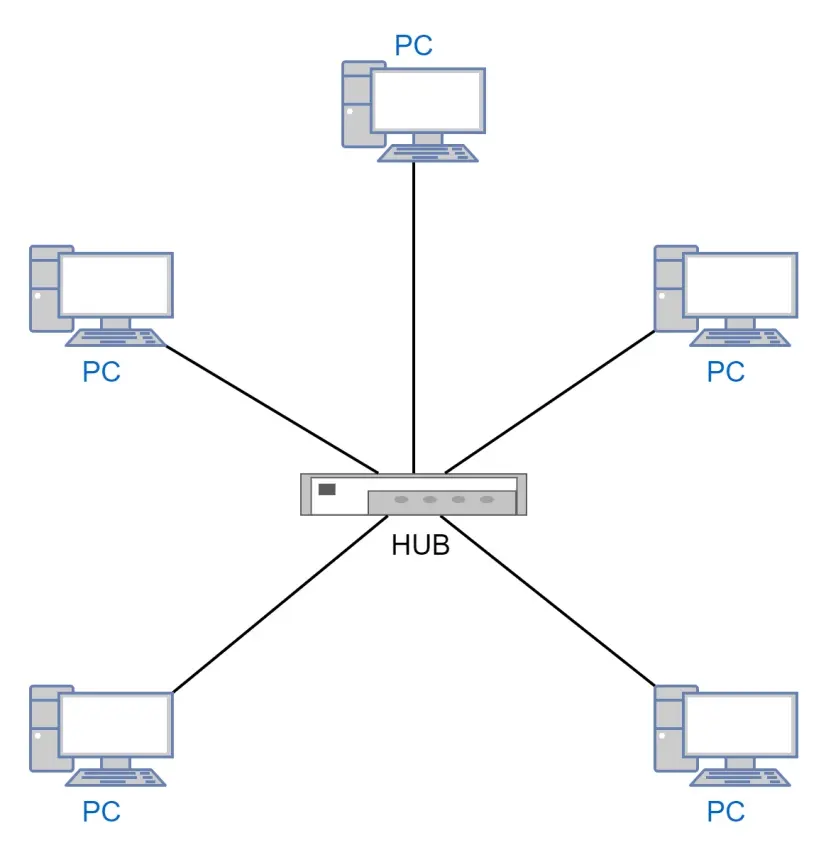
對等結構（point-to-point），這是星型拓撲的擴充套件，在本文中用於分析通訊複雜度下限時。

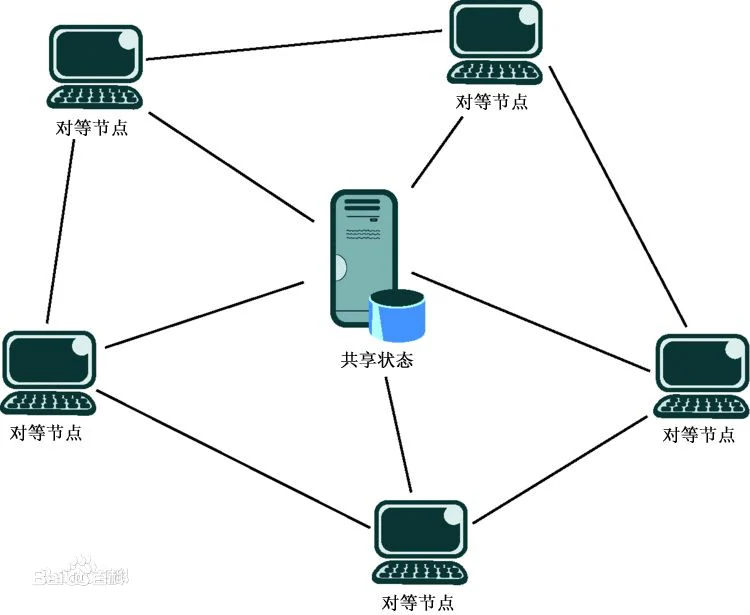
另外還有廣播型場景：
。。。待補充

其他介紹

兩方閾值PSI

在CRYPTO 2019中已經介紹很清晰了，使用的是AHE構造的兩方閾值PSI，通訊複雜度為\(\widetilde{O}(T^2)\)。

亞線性通訊PSI

本文設計的多方閾值PSI可以用於設計多方PSI，其通訊複雜度只與差值大小相關。具體說，對於多方閾值PSI，閾值\(T=2^0,...,2^k\)，其通訊複雜度是單個範例的\(logT\)倍，所以實現了通訊複雜度為亞線性（對於集合大小）的多方PSI。

單個範例是啥？

緊湊型MPC

緊湊型的MPC，即通訊複雜度不隨函數的輸入增長而增長。

當前發展

1、CRYPTO 2019中最後給出擴充套件為多方的構想，但只要考慮了\(F_{TPSI-int}\)，首次使用TFHE用於cardinality testing，通訊複雜度為\(O(nT)\)，在求交階段使用 MPC 協定來計算隨機多項式，其中通訊複雜度取決於 MPC 。
2、Multiparty Cardinality Testing for Threshold Private Set-2021：解讀中給出了多方閾值PSI的方案，也同樣沒有介紹\(F_{CTest-diff}\)。

基礎知識

符號

1、\(\lambda\)是安全引數；\(poly(\lambda)\)是關於\(\lambda\)的多項式函數；\(negl(\lambda)\)是不可忽略函數，即對於一個函數\(f(.)\)、任意的多項式\(p(.)\)和足夠大的\(\lambda\)，使得\(f(\lambda)<1/p(\lambda)\)成立。
2、\([x]\)，表示加密的\(x\)。
3、\(\widetilde{O}(x)=O(x.poly(x))\)：隱藏polylog因子。

多方計算的安全性

UC安全參考：安全性證明



下面做簡單描述：
\(\Pi\)是協定，\(n\)個參與者，\(F\)是理想函數。
1、真實世界執行
各方執行協定\(\Pi\)，可以呼叫功能函數\(G\)，環境\(Z\)選擇各方的輸入，代替敵手，可以破壞參與方的任何集合以獲得額外資訊。\([Z,\Pi,G]\)是真實世界中\(Z\)的輸出

2、理想世界執行
\(n\)個參與方將輸入傳送給理想函數\(F\)，返回計算結果，其中\(SIM\)作為理想世界中的敵手，可以模模擬實世界中執行中的環境\(Z\)，能夠完全控制被腐敗的參與者並模仿參與者對\(Z\)的view。\([Z,SIM,F]\)是理想世界中\(Z\)的輸出

協定\(\Pi\)是安全的，需滿足：對於任意的PPT的\(Z\)，都存在PPT的\(SIM\)，滿足：

TFHE

本文中使用的是【Threshold cryptosystems from threshold fully homomorphic encryption-2018】

方案如下：

總結：
（1）這裡的公鑰和私鑰都是多個
（2）這裡的解密是部分解密，然後通過聚合全部解密結果才能完全恢復明文。

緊湊性

如果一個同態加密方案的解密電路是獨立於計算函數的，即密文的長度與計算電路的深度無關，則稱該同態加密方案是緊湊的。


總結：
（1）這裡的\(Eval和ParticalDec\)都是同態計算，輸出的計算密文與電路深度無關。

正確性

正確性，就是檢測計算後的密文解密和對明文計算一樣。

安全性

分為語意安全（Semantic Security）和模擬安全（Simulation Security）

1、語意安全

語意安全就是任意PPT的敵手不能區分任意兩個明文的密文。


具體來講：
（1）敵手任意模擬一個參與者\(S_i\)，對於兩個任意明文\((m_0,m_1)\)，傳送\((S_i,{pk_i,sk_i},(m_0,m_1)\)給挑戰者
（2）挑戰者任選一個\(m_b\)加密發給敵手
（3）敵手輸出猜測值\(b'\)，若\(b=b'\)，則敵手獲勝，輸出1，否則，相反。

2、模擬安全

模擬安全，是存在一個模擬器SIM，對於任意PPT的敵手\(A\)，使得兩個方案\(Expt_{TFHE.Real}(1^{\lambda })\)和\(Expt_{TFHE.Ideal}(1^{\lambda })\)在計算上是不區分的。

TAHE

1、和TFHE不同之處：
（1）\(Eval\)中的計算電路\(C\)是線性的，即只能進行\(ax+b\)之類的計算
（2）只有加法同態性
2、給出常用的TAHE方案：

來源於：Scalable multi-party private set-intersection

（1）Paillier變體：https://github.com/niclabs/tcpaillier
（2）ElGamal變體：https://github.com/aistcrypt/Lifted-ElGamal

3、密文具有隨機性，不可區分

引理


總結：
（1）2.3說的是在計算\(V(x)\)時，所選的\(R(x)\)和編碼後的多項式\(p(x)\)時互素的。
（2）2.4說的是若\((p_1(x),...,p_n(x))\)是互素的，那麼\((p_1‘(x),...,p_n’(x))\)也是互素的，其中\(p_j'(x)=p(x).(x-r_i)\)。
（3）2.5說的是若\((p_1(x),...,p_n(x))\)是互素的，且\(deg(p_i(x))=\alpha\)，則對於隨機選取的\((R_1(X),...,R_n(X)\)（其\(deg(R_j(x))=\beta\geq \alpha\)），那麼\(U(x)=\sum_{i=1}^{n}(p_i(x).R_i(x)\)也是隨機的。

主要技術

這裡選用\(P_1\)作為leader方（designated party）

基於TFHE的\(F_{CTest-int}\)

即使用TFHE去判斷交集是否足夠大！


（1）這裡\(p(x)\)的分子分母（消去後的）的degree為\(m-|I|\)，如果\(m-|I|=|S_A\setminus I|\leq T\)，則\(deg(p(x))\leq 2T\)，即可以用\(2T+1\)個點值對插值出\(p(x)\)。
（2）求出\(p(x)\)後，就可以求出其分母\(p_{A\setminus I}(x)\)，其根就是集合\(S_{A}\setminus I\)

下面是具體的兩方協定：

（1）通過\(2T+1\)個陣列成\(2T+1\)個點值對，從而插值出有理函數\(p(x)\)
（2）這裡使用的是FHE，通過同態的判斷\(Enc(p(z))\)是否和\(p_B(z)/Enc(p_A(z))\)相等，決定兩方資料集是否相似。為什麼呢？因為若\(Enc(p(z))=p_B(z)/Enc(p_A(z))\)，則\(deg(p(x))\leq 2T\)，從而\(m-|I|=|S_A\setminus I|\leq T\)，則差集最大為\(T\)，兩集合相似。

以上兩方協定是CRYPTO 2019:The Communication Complexity of Threshold Private Set Intersection-2019：解讀中給出的，下面根據這個兩方協定，擴充套件為多方。


（1）擴充套件為多方後，就需要使用TFHE了
（2）決定多方資料集是否相似，還是通過判斷\(Enc(p(z))\)是否和\(Dec(p_2(z))+...+Enc(p_n(z))/p_1(z)\)相等。
（3）注意這裡是\(P_i\)方加密，發給\(P_1\)，在兩方中，是\(P_1\)加密，傳送給其他方。

這樣簡單改造為多方是有問題的：分子分母中不屬於交集的項也能消去！


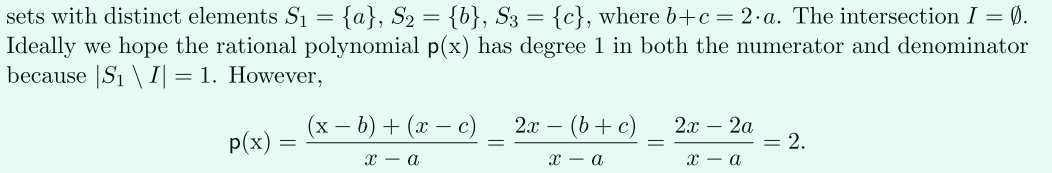
（1）這裡元素\(a\)不屬於交集，但還是消去了。

如何解決呢？CRYPTO 2019中給出的方法是，加亂數！


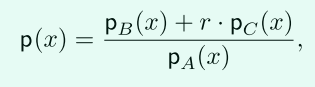
這裡給出的方法是加入亂數構成的隨機項：

（1）在每一個多項式中加入一個隨機項，這樣不相同的元素就不會通過某些計算結合消去了。

基於TFHE的\(F_{CTest-diff}\)

即使用TFHE判斷差集是否足夠小！


（1）\(P_i\)與其他參與方\(P_i\)互動後都會插值出一個\(\widetilde{p_i}(x)\)，從而可以得到\(p_{i\setminus 1}(x)\)和\(p_{1\setminus i}(x)\)，所以能計算出差集\(D_{1,i}=S_1\setminus S_i\)和\(D_{i,1}=S_i\setminus S_1\)。
（2）這裡存在一個等價關係：\(|\bigcup S_i\setminus I|\leq T \approx |S_i\setminus I|\leq T \approx deg(\widetilde{p_i}(x))\leq 2T\) 。
（3）因為\(\bigcup S_i\setminus I\)中的資料，存在兩種情況，所以\(P_1\)不僅需要計算出差集，還要判斷\(|\bigcup S_i\setminus I|\)和\(T\)的大小。

基於TAHE的\(F_{CTest-diff}\)

即使用TAHE判斷差集是否足夠小！
本文給出的方法能將兩方的通訊複雜度降為\(\widetilde{O}(T)\)。

1、兩方場景下：


（1）現在cardinality testing的問題是，判斷\(deg(p(x))\leq 2T\)是否成立？CRYPTO 2019給出的方法判斷\(p(x)\)是否是「稀疏」的（該思想來自【A local decision test for sparse
polynomials】），即通過判斷漢克爾矩陣\(H\)的奇異性（判斷方法來自【Secure linear algebra using linearly recurrent sequences】）
（2）該方法的通訊複雜度為\(\widetilde{O}(T^2)\)。

2、該文中給出的方法：

（1）使用另外一種方法（half-GCD）去檢測漢克爾矩陣奇異性（來自【Fast solution of Toeplitz
systems of equations and computation of pad´e approximants】），能將通訊複雜度降低為\(\widetilde{O}(T)\)。
（2）如何使用：Alice和Bob各自計算出矩陣的分享份\(H_i\)，然後通過2PC或者GC聯合計算出\(H\)，再去判斷奇異性。

3、擴充套件為多方的思路：

（1）首先要設計一個多項式\(f(x)\)，使其\(deg(f(x))=|\bigcup S_i\setminus I|\)。
（2）然後在各方運算是線性的，各方可以從這個多項式中獲取矩陣的分享份。
（3）最後各方執行MPC，檢測矩陣的奇異性。

計算交集

這部分是在cardinality testing通過後，如何計算交集。

1、兩方場景

這是CRYPTO 2019中給出的方法



（1）Alice根據\(2T+1\)個點插值出\(p(x)\)。
（2）再根據\(f(x)=p_B(x)/p_A(x)=p_{B\setminus A}/p_{A\setminus B}\)，恢復出分母\(p_{A\setminus B}\)
（3）但是不安全：Alice不僅可以恢復出分母，也能恢復出分子，洩漏Bob的資料。正如上面介紹的，這裡給出的解決辦法是加入噪音多項式\(V(x)\)：

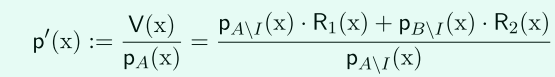
這樣\(deg(p'(x))\leq 3T\)，這裡給出\(3T+1\)個點插值出\(p'(x)\)，此時Alice就不能從分子中得到額外的Bob資訊了。
（4）重要的就是\(V(x)\)是如何構造出的來的！

2、多方場景

這部分是沿著CRYPTO 2019兩方擴充套件為多方的思想構造的。


（1）這裡要求各方\(P_i\)選取degree為\(T\)的\(n\)個隨機多項式\((R_{i,1},...,R_{i,n})\)
（2）然後\(P_1\)也根據\(3T+1\)個點插值出\(p'(x)\)，進而得到分母，這樣由於\(V(x)\)足夠隨機，不會洩漏其他方的資料，能得到交集。

3、存在的問題

（1）上述介紹多方場景，其通訊複雜度為\(O(n^2T)\)，存在的消耗主要是，各方\(P_i\)選取degree為\(T\)的\(n\)個隨機多項式\((R_{i,1},...,R_{i,n})\)。
（2）經過分析，各方只需要選取兩個隨機多項式就能達到效果，第一個多項式用於隨機化自己插值出來的多項式，第二個用於隨機化其他方插值出來的多項式。
（3）下面根據該思想，基於TFHE設計的協定通訊複雜度可以降低為\(O(nT)\)

低通訊量



（1）在對等網路模型下，多方閾值PSI的通訊複雜度的下限為\(\Omega(nT)\)
（2）在廣播模型下，多方閾值PSI的通訊複雜度的下限為\(\Omega(Tlogn+n)\)

下面分析在對等模型下的兩種情況的通訊複雜度下限。

1、求交集\(F_{TPSI-int}\)

（1）意思是在一個能抵抗半誠實攻擊的多方閾值PSI中，兩兩互動的通訊複雜度為\(\Omega(T)\)

（1）很明顯，多個一起互動的總通訊複雜度為\(\Omega(nT)\)
2、求差集\(F_{TPSI-diff}\)

這裡說，\(F_{TPSI-diff}\)和\(F_{TPSI-int}\)不同之處是，前者是當\(|(X_1\setminus X_2)\cup (X_2\setminus X_1)|\leq T\)時，各方才會求交。【嗯，，為什麼呢。。】


（1）意思是在一個能抵抗半誠實攻擊的多方閾值PSI中，兩兩互動的通訊複雜度為\(\Omega(T)\)

（1）很明顯，多個一起互動的總通訊複雜度為\(\Omega(nT)\)

基於TFHE的測試

這部分，給出關於cardinality testing的兩種協定，即\(F_{CTest-int}\)測試交集是否足夠大(大於\(m-T\))，和\(F_{CTest-diff}\)測試差集是否足夠小（小於\(T\)）！

\(F_{CTest-int}\)

判斷交集是否足夠大！


（1）各方編碼得到自己的多項式後，乘以一個隨機項，以隨機化分子分母，解決「分子分母可以相互消去不相同的項」的問題。
（2）leader方（\(P_1\)）選取一個隨機值\(z\)共用給其他方
（3）各方（不含leader）將\(2T+3\)個點和\(z\)帶入到各自的多項式\(p_i'(x)\)中，在加密得到得到\([e_{i,j}]\)和\([e'_i]\)發給leader
（4）leadre根據：

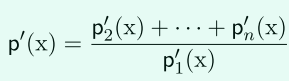
計算出\(2T+3\)個點值對：

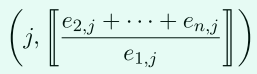
然後leader根據這些點插值出\([p^*(x)]\)。
（5）若\(deg([p^*(x)])\leq 2T+2\)，則\(p^*(x)=p(x)\)，所以這裡需要判斷\(p^*(x)=p(x)\)是否成立，這裡是判斷
\(p^*(z)\)和\(e'_2+...+e'_n/e'_1\)是否相等？

下面分析一波正確性：

1、這是符合條件的，即交集足夠大，\(|I|\geq m-T\)

（1）經過相同項消去後，分子和分母的最大級數（degree）為\(T+1\)，所以\(p'(x)\)最大級數為\(2(T+1)\)，即需要\(2T+3\)個點才能插值出來。

2、這是不符合條件的，即交集不足夠大，\(|I|< m-T\)


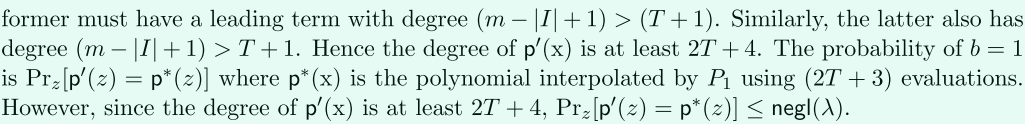
（1）對於分子和分母的級數，有\((m-|I|+1)>(T+1)\)，（因為，\(|I|< m-T\)，說明差集大於\(T\)，即\((m-|I|)>T\)），則\(p'(x)\)最大級數大於\(2(T+1)\)，即最小為\(2T+3\)，至少需要\(2T+4\)個點才能插值出來，這裡只有\(2T+3\)點。

下面是通訊量


（1）\(O(1)\)輪，通訊量為\(O(nTpoly(\lambda ))\)

總的來說，這裡是想要判斷交集是否足夠大，即\(|S_i\setminus I|\leq T\)是否成立？規約到\(deg([p^*(x)])\leq 2T+2\)是否成立？再規約到判斷\(p^*(z)\)和\(e'_2+...+e'_n/e'_1\)是否相等？

這裡留一個疑問：4-(b)中如何判斷密態的\(p^*(z)\)和\(e'_2+...+e'_n/e'_1\)是否相等？

\(F_{CTest-diff}\)

判斷差集是否足夠小！即判斷\(|\bigcup S_i\setminus I|<T\)是否成立，實現方法是各方與leader互動，leader知道兩方差集的加密，根據判斷所有差集的交集大小是不是不大於\(T\)來實現的。


（1）首先各方先將自己資料編碼為多項式\(p_i(x)\)，然後將\(2T+1\)個點和\(z\)帶入得到\(e_{i,j}\)和\(e'_i\)（\(z\)是\(P_1\)隨機選取的）
（2）各方（除leader外）將\(e_{i,j}\)和\(e'_i\)加密，發給leader；leader就可以根據：

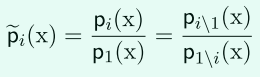
計算出\(2T+1\)個點\((j,[e_{i,j}/e'_i])\)，從而插值出\(\widetilde{p^*}(x)\)，從而得到分子和分母，所以就能得到兩方各自的差集\([D^*_{i,1}],[D^*_{1,i}]\)。若\(deg(\widetilde{p^*}(x))\leq 2T\)，則\(\widetilde{p^*}(x)=\widetilde{p}(x)\)；反過來說，只需要判斷\(\widetilde{p^*}(x)=\widetilde{p}(x)\)是否成立，就能判斷\(deg(\widetilde{p^*}(x))\leq 2T\)？

這時\(z\)就上場了，leader通過判斷\(\widetilde{p^*}(z)=e'_i/e'_1\)是否成立，進而判斷\(deg(\widetilde{p^*}(x))\leq 2T\)？若相等，\(b_i=1\)，否則為0
（3）leader得到了各方與自己相比的所有差集，這時需要判斷所有差集並在一起的數量是否不大於\(T\)，若是，則\(b'=1\)，否則為0。
（4）最後leader將密態的\(b'\)和\(b_i\)相乘得到密態的\(b\)，然後聯合解密判斷差集是否足夠小！

總結

  • 給出了兩種閾值判斷標準：（1）交集足夠大（2）差集足夠小 時才去求交
  • 分別基於TFHE和TAHE構造以上兩種情況
  • 基於TFHE的是基於CRYPTO 2019中的思想
  • 該文章有程式實現：https://www.cnblogs.com/pam-sh/p/16479540.html
  • 基於同態的還是太慢，通訊複雜度沒有較大提升。