深入淺出零錢兌換問題——揹包問題的套殼
深入淺出零錢兌換問題——揹包問題的套殼
前言
在本篇文章當中主要通過介紹兩個演演算法題,從最基本的問題開始深入淺出零錢兌換問題,幫助大家從動態規劃的本源深入理解問題當中的原理,並且學會自己分析問題,分析資料之間的依賴關係,通過分析這種關係自己推導演演算法的優化過程,再也不怕類似於揹包問題的演演算法題了。
零錢兌換
題目
給你一個整數陣列 coins ,表示不同面額的硬幣;以及一個整數 amount ,表示總金額。
計算並返回可以湊成總金額所需的 最少的硬幣個數 。如果沒有任何一種硬幣組合能組成總金額,返回 -1 。
你可以認為每種硬幣的數量是無限的。
範例
範例1
輸入:coins = [1, 2, 5], amount = 11
輸出:3
解釋:11 = 5 + 5 + 1
範例2
輸入:coins = [2], amount = 3
輸出:-1
狀態表示和狀態轉移方程
在求解動態規劃問題的時候通常的步驟有以下幾個:
- 尋找能夠表示狀態的陣列
dp,即我們需要尋找dp的含義,分析需要用幾緯陣列表示具體的狀態。 - 通過分析問題,尋找動態轉移公式。
- 初始化狀態陣列。
- 通過分析動態轉移方程,確定陣列的遍歷順序。
狀態表示陣列
在揹包問題當中通常都是用一個二維陣列表示資料的狀態,在這個問題當中我們使用一個二維陣列dp表示我們需要的狀態:
dp[i][j]表示使用coins前i種面額的硬幣表示金額等於j時使用的最少的金幣,那麼我們最終答案就是dp[N][amount],他表示使用coins陣列當中所有面額的硬幣表示amount需要的最少的硬幣個數。
尋找動態轉移方程
在確定了狀態表示的陣列之後,現在我們就需要分析出動態轉移方程了,在這個問題當中對於每一種面額的硬幣我們都有兩種選擇:選和不選,但是在這個問題當中題目已經說明了對於每一種貨幣都可以認為是無限的,如果我們不選擇,那這種情況比較簡單,但是如果選擇了這種情況就比較複雜了:
- 不選,這種情況比較簡單,比如對於
dp[i][j],如果第i種面額的貨幣不選擇,那麼說明只使用前i - 1種面額的貨幣,那麼dp[i][j] = dp[i - 1][j],也就是說明如果使用前i種面額的貨幣去表示總額為j,但是不選擇第i種面額的貨幣,就相當於使用前i-1種貨幣去表示j,那麼需要的貨幣個數跟使用前i-1種貨幣去表示j需要的貨幣數目是相等的。 - 選,這種情況看起來就比較複雜了,因為我們需要確定是選一次,還是選兩次,......,還是選N次,但是其實仔細思考一下我們可以使用一個類似遞迴的形式去解決這個問題,如果選擇那麼
dp[i][j] = dp[i][j - coins[i]] + 1,我們仔細分析一下這個公式,相當於在總金額等於j的情況下先使用一次第i個面額的硬幣,但是因為我們的硬幣是無限的,現在我們還是可以選擇第i個硬幣,相當於總金額等於j - coins[i]而且可以使用前i個硬幣的情況下,需要的最少的硬幣個數,這就解決了是選一次還是選N次的問題了,而在上面的公式當中加一的原因是使用了一次第i種硬幣。
很顯然我們需要從上面兩種情況當中選擇需要的硬幣最少的一種方法,因此綜合上面的結果又如下的動態轉移方程:
其實上面這個問題的分析過程跟完全揹包可以說是一模一樣,如果你對完全揹包感興趣,你可以閱讀這篇文章完全揹包。
初始化狀態陣列
上面的問題分析過程當中,我們已經分析出來了動態轉移方程,這個過程和完全揹包非常相似,但是這個問題比完全揹包還稍微複雜一點,因為不一定能夠尋找到這樣一種組合湊成的總金額等於題目當中規定的數目。我們用-1表示找不到這樣一種組合能夠表示。
- 在正式初始化之前先將
dp陣列第一行當中的資料全部初始化為-1。 - 初始化第一行程式碼如下:
for (int i = 0; i * coins[0] <= amount; i++) {
dp[0][i * coins[0]] = i;
}
dp陣列的第一行表示只使用第一種面額的硬幣,因此只有第一種硬幣面額的整數倍總金額才能使用第一種硬幣進行表示,而且對應的硬幣個數等於\(\frac{amout}{coins[0]}\)。
再看狀態轉移陣列:
- 如果
dp[i][j - coins[i]] == -1,那麼就不能通過選擇第i種硬幣進行表示,在這種情況下,我們只能通過選擇前i-1一種貨幣進行表示,即dp[i][j] = dp[i - 1][j]。可你你會有疑問,如果也不能使用前i-1種物品進行表示呢?沒關係,如果不能表示那麼dp[i - 1][j] == -1,那麼賦值之後dp[i][j]也等於-1,也是不能表示的。 - 如果
dp[i][j - coins[i]]不等於-1,但是dp[i - 1][j]等於-1,那麼dp[i][j] = dp[i][j - coins[i]] + 1。 - 如果兩者都不等於-1,那麼我們就有如下的狀態轉移公式了:
程式碼
class Solution {
public int coinChange(int[] coins, int amount) {
int[][] dp = new int[coins.length][amount + 1];
Arrays.fill(dp[0], -1);
for (int i = 0; i * coins[0] <= amount; i++) {
dp[0][i * coins[0]] = i;
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
// 如果要使用對應的硬幣
// 總金額數目肯定要大於硬幣的面額
if (j >= coins[i]) {
if (dp[i][j - coins[i]] == -1)
dp[i][j] = dp[i - 1][j];
else if (dp[i - 1][j] == -1)
dp[i][j] = dp[i][j - coins[i]] + 1;
else
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - coins[i]] + 1);
} else {
// 否則只能使用前 i-1 種硬幣
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[coins.length - 1][amount];
}
}
上面的程式碼體現的就是完全揹包 的思想,在題目當中硬幣可以使用無限次,如果只能使用一次的話,問題就轉換成01揹包了,那麼動態轉移方程就為:
單行陣列優化
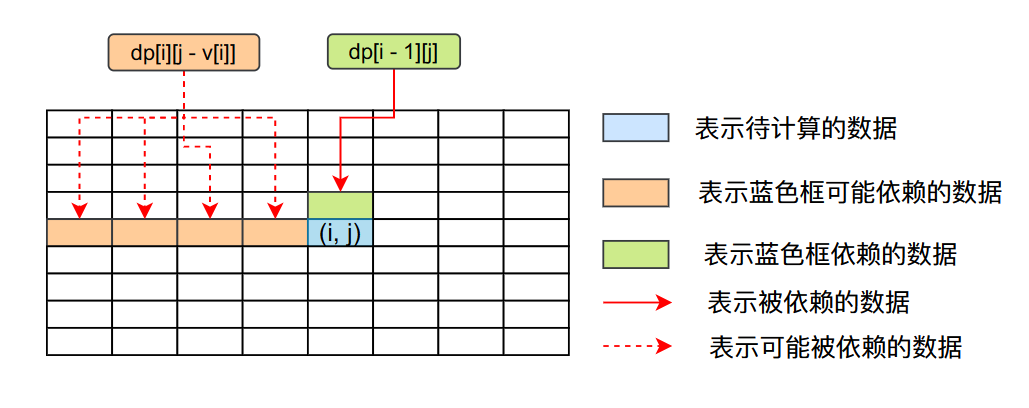
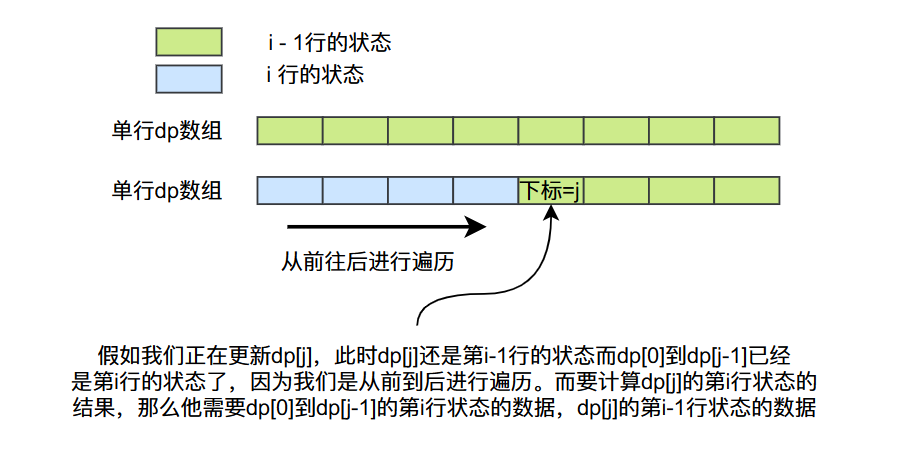
根據動態轉移方程\(dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i]] + 1)\),我們可以得到dp陣列當中資料之間的依賴關係,他們的關係如上圖所示,dp[i][j]依賴的資料為它上一行同列的位置,和第i行前面的某些資料,事實上我們可以使用單行陣列去進行實現,我們使用的迴圈還是一樣的,但是使用的陣列有所變化,從之前的二維陣列變成一維陣列。當我們遍歷到單行陣列第j個資料的時候,第j個資料還是上一行的狀態,但是單行陣列的下標從0到j-1的位置資料的狀態已經從上一行更新了,這些資料的狀態相當於二維陣列的dp[i]這一行的狀態,而這正好可以滿足動態轉移方程的需求,因為在動態轉移方程當中,dp[i-1][j]依賴的資料全部符合條件,單行陣列當中的下標為j資料等於dp[i][j],單行陣列下標為x的資料等於dp[i][x],其中\(0 \le x \le j\),這裡你可以結合程式碼、文字和圖片進行理解,理解效果會更加好一點。
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, -1);
dp[0] = 0;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
if (dp[j - coins[i]] != -1) {
if (dp[j] == -1) {
dp[j] = dp[j - coins[i]] + 1;
}else
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount];
}
}
另一種角度思考問題
在上面的文章當中,我們是使用-1去表示不能夠找到一個組合滿足總金額數目。我們可以先將陣列當中所有的資料全部初始化成amount + 1,這個是硬幣的上界,如果我們全部使用一塊的硬幣進行兌換,結果是amount,因此最大的值不會超過amount + 1,因為在動態轉移方程當中求的是最小值,因此在進行狀態轉移的時候不會選擇這個值,因此下面的程式碼也是正確的!!!
class Solution {
public int coinChange(int[] coins, int amount) {
int max = amount + 1;
int[] dp = new int[amount + 1];
for (int j = 0; j < dp.length; j++) {
dp[j] = max;
}
dp[0] = 0;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
if (dp[j - coins[i]] != max) {
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == max ? -1 : dp[amount];
}
}
零錢兌換 II
題目
給你一個整數陣列 coins 表示不同面額的硬幣,另給一個整數 amount 表示總金額。
請你計算並返回可以湊成總金額的硬幣組合數。如果任何硬幣組合都無法湊出總金額,返回 0 。
假設每一種面額的硬幣有無限個。
題目資料保證結果符合 32 位帶符號整數。
範例
範例1
輸入:amount = 5, coins = [1, 2, 5]
輸出:4
解釋:有四種方式可以湊成總金額:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
範例2
輸入:amount = 3, coins = [2]
輸出:0
解釋:只用面額 2 的硬幣不能湊成總金額 3 。
狀態表示和狀態轉移方程
狀態表示陣列
在這個問題當中我們也是使用一個二維陣列表示我們的狀態dp[i][j]。這個表示使用前i個硬幣,總金額為j的情況下,能夠找到多少種組合方式,是硬幣的和等於總金額數。
在這道題目當中我們也可以使用無數次硬幣,因此這也是一個完全揹包問題。
尋找動態轉移方程
對於每一種硬幣同樣的有兩種情況選擇和不選擇,每一種情況都有不同的組合,因此最終的組合數目就是將這兩個結果相加:
- 選擇,在這個情況下我們能夠獲得不同的組合數就是
dp[i][j - coins[i]],這個程式碼的含義就是選擇一次第i個硬幣,因為有無數個硬幣,因此這個結果就等於使用前i個硬幣組合總金額為j-coins[i]時,一共有多少個組合。 - 不選擇,如果不進行選擇,那麼就相當於使用前
i - 1個硬幣,組合總金額為j時,一共有多少個組合。
因此最終的組合數的個數就是上面兩種方式的不同組合個數相加,因此我們的動態轉移方程為:
初始化狀態陣列
在初始化dp陣列的第一行的時候,只有是第一個硬幣的整數倍的總金額才能進行匹配,如果不能匹配,那麼不同的組合的數目就等於0,能夠進行匹配的組合數也只有一個,那就是使用的硬幣全是第一種硬幣。在這裡需要注意的是當總金額等於0的時候,也是有一種組合方式的,那就是沒有一個硬幣,這也是一種組合方式,就相當於集合的空基,因此初始化程式碼如下:
for (int i = 0; i * coins[0] <= amount; i++) {
dp[0][i * coins[0]] = 1;
程式碼
class Solution {
public int change(int amount, int[] coins) {
int[][] dp = new int[coins.length][amount + 1];
// dp[i][j] 的含義:前 i 個錢 容量 j 有多少種方法
for (int i = 0; i * coins[0] <= amount; i++) {
dp[0][i * coins[0]] = 1;
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
if (j >= coins[i]) {
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
} else
dp[i][j] = dp[i - 1][j];
}
}
return dp[coins.length - 1][amount];
}
}
其實這道題也有對應的01揹包問題,在這道題目當中是完全揹包問題的變種,如果所有的硬幣只能夠使用一次的話,那麼動態轉移方程如下:
單行陣列優化
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
// dp[i][j] 的含義:前 i 個錢 容量 j 有多少種方法
dp[0] = 1;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++)
dp[j] += dp[j - coins[i]];
}
return dp[amount];
}
}
這個優化的原理和第一題也是一樣的,通過分析動態轉移方程,看單行陣列是否能夠滿足動態轉移方程的要求,如果能夠滿足的話,那就能夠進行單行陣列優化,反之不能進行優化,而在這個問題當中,資料依賴關係和第一題是一樣的,dp[i][j]依賴的資料是dp[i - 1][j]和dp陣列第i行前j - 1個資料,根據第一題的分析,我們是可以使用單行陣列進行優化的!!!
總結
在本篇文章當中主要給大家介紹了兩道零錢兌換的問題,在本文當中的這兩道題目都是屬於完全揹包的變種,如果要徹底弄懂這個問題的話就需要好好分析動態轉移方程和資料之間的依賴關係,通過分析資料之間的依賴關係,我們自己也可以從零推導優化過程。在這兩道問題當中硬幣都可以使用無數次,如果將能夠使用的硬幣只能夠使用一次的話,那麼這個問題就變成01揹包的變種問題了。
更多精彩內容合集可存取專案:https://github.com/Chang-LeHung/CSCore
關注公眾號:一無是處的研究僧,瞭解更多計算機(Java、Python、計算機系統基礎、演演算法與資料結構)知識。