AlexNet—論文分析及復現
AlexNet折積神經網路是由Alex Krizhevsky等人在2012年的ImagNet影象識別大賽獲得冠軍的一個折積神經網路,該網路放到現在相對簡單,但也是深度學習不錯的折積神經網路。論文:《ImageNet Classification with Deep Convolutional Neural Networks》

論文結構
-
Abstruct:簡單介紹了AlexNet的結構及其成果
-
Introduction:神經網路要是有更快的GPU和更大的資料集我們的結果就會得到改善
-
The Dataset:介紹ILSVRC-2010和ImageNet資料集
-
The Architecture:ReLU非線性函數介紹、兩個GPU進行訓練、區域性響應歸一化、 Overlapping Pooling、整體架構
-
Reducing Overfitting:對抗過度擬合的方法,資料增強和Dropout
-
Details of learning:超引數的設定,權重及偏置的初始化
-
Results:介紹了AlexNet在比賽中獲得的成果,效能評估(Qualitative Evaluations):顯示預測正確的概率,同一類的影象特徵的歐式距離更近
-
Discussion:結果有了很大的改善,但是在某些方面還是有很多工作要做
AlexNet折積神經網路的特點
1.非線性啟用函數ReLu
在AlexNet出現之前,sigmoid是最為常用的非線性啟用函數。sigmoid函數能夠把輸入的連續實值壓縮到0和1之間。但是,它的缺點也非常明顯:當神經網路層數過多或輸入值非常大或者非常小的時候會出現飽和現象,即這些神經元的梯度接近0,因此存在梯度消失問題。
影象程式碼:
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
影象:
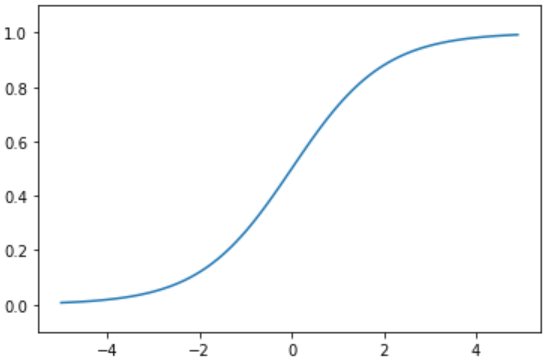
tanh函數(雙曲正切啟用函數)很像是sigmoid函數的放大版。在實際使用中要略微優於sigmoid函數,因為它解決的中心對稱問題。指數的計算複雜,計算成本高。梯度消失(梯度彌散)的特點依舊保留,因為兩邊的飽和性使得梯度消失,進而難以訓練。
影象程式碼:
import numpy as np
import matplotlib.pyplot as plt
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y=tanh(x)
plt.plot(x,y)
plt.show()
影象:
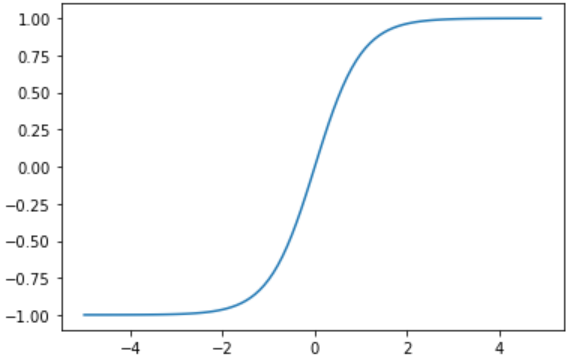
具體來說ReLU的好處有以下幾點:
1.可以使神經網路訓練更快
相比較於sigmoid和tanh,relu的求導速度更快
2.增加神經網路的非線性
ReLU是非線性函數
影象程式碼:
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0,x)
x=np.arange(-5.0,5.0,0.1)
y=relu(x)
plt.plot(x,y)
plt.show()
影象:
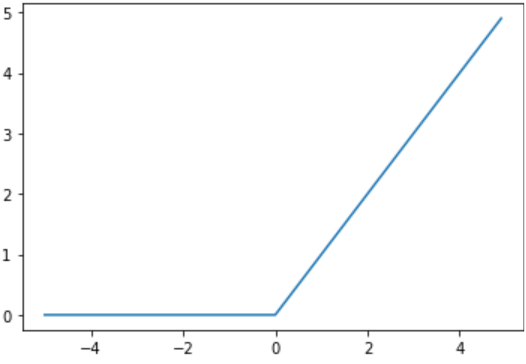
3.使神經網路具有稀疏性
可以使一些神經元輸出為0,可以增加網路的稀疏性
4.防止梯度消失
當數值過大或者過小時,sigmoid, tanh導數接近0, 會導致方向傳播時梯度消失的問題,relu為非飽和啟用函數不存在此問題
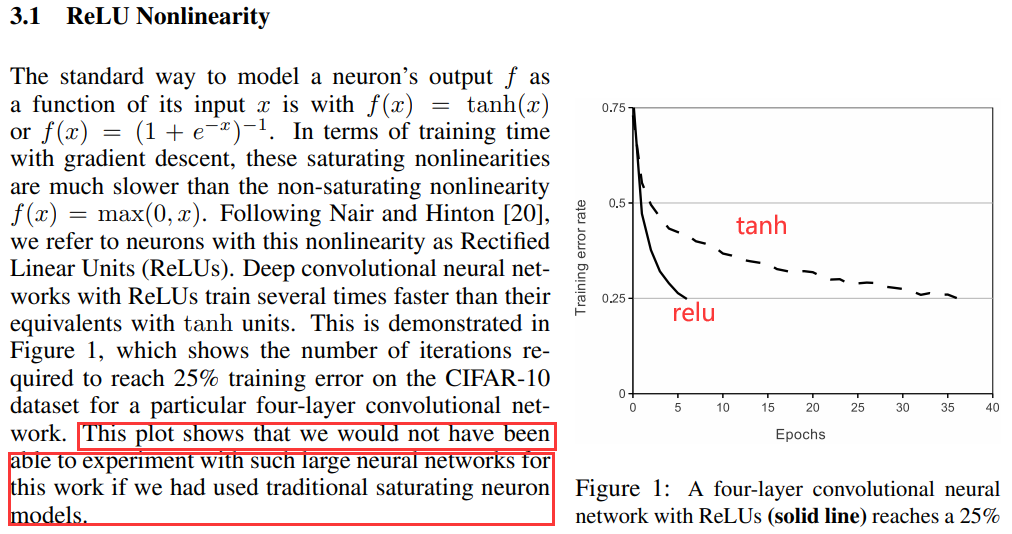
該圖表明,如果我們使用傳統的飽和神經元模型,我們將無法進行有如此大的神經網路的實驗
2.Local Response Normalization(區域性響應歸一化)
區域性響應歸一化(local response normalization,LRN)的思想來源於生物學中的「側抑制」,是指被啟用的神經元抑制相鄰的神經元。採用LRN的目的是,將資料分佈調整到合理的範圍內,便於計算處理,從而提高泛化能力。在神經網路中,我們用啟用函數將神經元的輸出做一個非線性對映,但是tanh和sigmoid這些傳統的啟用函數的值域都是有範圍的,但是ReLU啟用函數得到的值域沒有一個區間,可以在[ 0 , ∞ ] \lbrack 0,\infty \rbrack[0,∞],所以要對ReLU得到的結果進行歸一化。簡單理解,就是將利用當前第i ii個kernel的相鄰n − 1 n-1n−1個kernel對應( x , y ) (x,y)(x,y) 的值來做歸一化。論文中也給出了公式及介紹:

在2015年 Very Deep Convolutional Networks for Large-Scale Image Recognition.提到LRN基本沒什麼用,故這裡不做敘述。

在後來出現的一些CNN架構模型中LRN已不再使用,因為出現了更有說服力的歸一化——批次歸一化,即BN。
3.兩個GPU同時訓練

經過上述可知,兩 GPU 網路的訓練時間比單 GPU 網路略短。
4.Overlapping Pooling(重疊池化)
相對於傳統的no-overlapping pooling,採用Overlapping Pooling不僅可以提升預測精度,同時一定程度上可以減緩過擬合

相比於正常池化(步長s=2,視窗z=2) 重疊池化(步長s=2,視窗z=3) 可以減少top-1, top-5分別為0.4% 和0.3%;重疊池化可以避免過擬合。
5.Data Augmentation(資料增強)
論文中提到了兩種形式的Data Augmentation


隨機地從256 × 256的原始影象中擷取224 × 224大小的區域(以及水平翻轉的映象),相當於增加了\(2×(256-224)^{2}=2048\)倍的資料量,大大減輕過擬合,提升泛化能力。在進行測試的時候,取圖片的四個角加中間一共5個位置,並進行左右翻轉,一共獲得10張圖片,對他們在softmax層進行10次預測結果並求均值。
對影象的RGB資料進行PCA處理,並對主成分做一個標準差為0.1的高斯擾動,增加一些噪聲,可以讓錯誤率再下降1%。其中 pi 和 λi 是 RGB 畫素值的 3 × 3 協方差矩陣的第 i 個特徵向量和特徵值,對於特定訓練影象的所有畫素,每個 αi 僅繪製一次,直到該影象再次用於訓練,此時將重新繪製它。
6.Dropout
dropout可以讓模型訓練時,隨機讓網路上的一些節點失效(輸出置零),此時的權重值不會更新,但會儲存下來,因為這個過程只是對於本次訓練。
通常會給dropout設定一個比率為p,也就是說每個節點都有p的概率將會失效,這種技術減少了神經元的複雜協同適應,因為一個神經元不能依賴於特定其他神經元的存在。

如果沒有 dropout,我們的網路將表現出嚴重的過擬合。
AlexNet網路結構
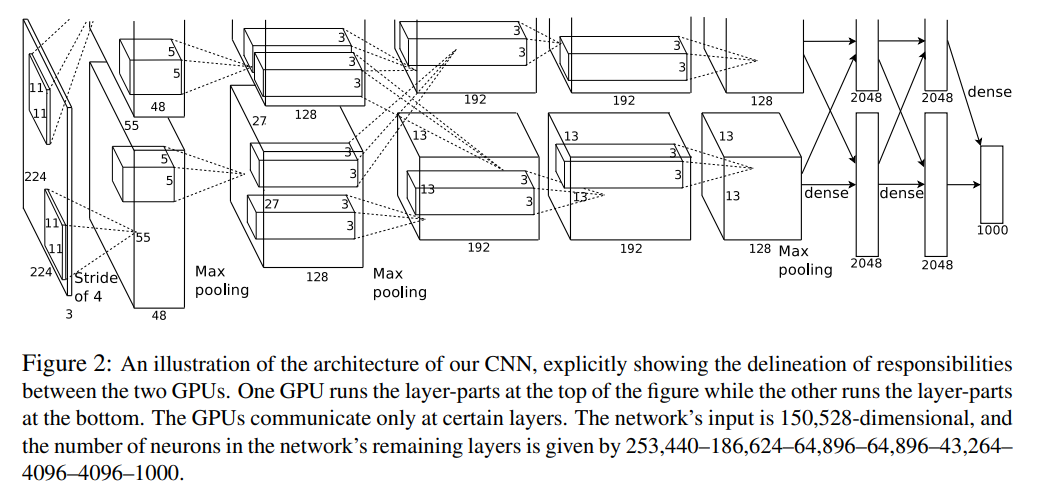
第一層折積
原論文中,AlexNet的輸入影象尺寸是224x224x3。但是實際影象尺寸為227x227x3,具體原因就不深究了,反正224x224x3不能推,227x227x3可以推。
第一個折積層為11x11x3,即折積核尺寸為11x11,有96個折積核,步長為4,折積層後緊跟ReLU,因此輸出的尺寸為 (227-11)/4+1=55,因此其輸出的每個特徵圖為 55x55x96,同時後面經過LRN層處理,尺寸不變。
最大池化層,池化核大小為3x3,步長為2,輸出的尺寸為 (55-3)/2+1=27,因此特徵圖的大小為:27x27x96。由於雙gpu處理,故每組資料有27x27x48個特徵圖,共兩組資料,分別在兩個gpu中進行運算。
第二層折積
每組輸入的資料為27x27x48,共兩組資料,在兩個GPU上訓練
每組資料都被128個折積核大小為: 5x5x48進行折積運算,步長為1,尺寸不會改變,同樣緊跟ReLU,和LRN層進行處理
最大池化層,池化核大小為3x3,步長為2,因此輸出兩組特徵圖:13x13x128
第三——五層折積
輸入的資料為13x13x128,共兩組,分別在兩個GPU上
第三層每組資料都被尺寸為 3x3x192的折積核進行折積運算,步長為1,加上ReLU,得到兩組13x13x192的畫素層
第四層經過padding=1填充後,每組資料都被尺寸大小為 3x3x192的折積核折積運算,步長為1,加上ReLU,輸出兩組13x13x192的畫素層
第五層經過padding=1填充後,每組資料都被尺寸大小為 3x3x128的折積核進行折積運算,步長為1,加上ReLU,輸出兩組13x13x128的畫素層
經過3x3池化視窗,步長為2,池化後輸出兩組6x6x256的畫素層
第六——八層全連線層
第六層:4096 個神經元+ ReLU
第七層:4096個神經元 + ReLU
第八層:1000 個神經元,最後一層為softmax為1000類的概率值
實現程式碼
採用的資料集為Fashion-MNIST,資料集地址為:Fashion-MNIST
利用tensorflow對AlexNet神經網路進行簡易實現
import tensorflow as tf
import numpy as np
# 載入資料
class DataLoader():
def __init__(self):
fashion_mnist = tf.keras.datasets.fashion_mnist
(self.train_images, self.train_labels), (self.test_images, self.test_labels) = fashion_mnist.load_data()
self.train_images = np.expand_dims(self.train_images.astype(np.float32)/255.0,axis=-1)
self.test_images = np.expand_dims(self.test_images.astype(np.float32)/255.0,axis=-1)
self.train_labels = self.train_labels.astype(np.int32)
self.test_labels = self.test_labels.astype(np.int32)
self.num_train, self.num_test = self.train_images.shape[0], self.test_images.shape[0]
def get_batch_train(self, batch_size):
index = np.random.randint(0, np.shape(self.train_images)[0], batch_size)
#need to resize images to (224,224)
resized_images = tf.image.resize_with_pad(self.train_images[index],224,224,)
return resized_images.numpy(), self.train_labels[index]
def get_batch_test(self, batch_size):
index = np.random.randint(0, np.shape(self.test_images)[0], batch_size)
#need to resize images to (224,224)
resized_images = tf.image.resize_with_pad(self.test_images[index],224,224,)
return resized_images.numpy(), self.test_labels[index]
dataLoader = DataLoader()
# 搭建模型
net = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(filters=96,kernel_size=11,strides=4,activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.MaxPool2D(pool_size=3, strides=2),
tf.keras.layers.Conv2D(filters=256,kernel_size=5,padding='same',activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.MaxPool2D(pool_size=3, strides=2),
tf.keras.layers.Conv2D(filters=384,kernel_size=3,padding='same',activation='relu'),
tf.keras.layers.Conv2D(filters=384,kernel_size=3,padding='same',activation='relu'),
tf.keras.layers.Conv2D(filters=256,kernel_size=3,padding='same',activation='relu'),
tf.keras.layers.MaxPool2D(pool_size=3, strides=2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(4096,activation='relu'),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(4096,activation='relu'),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(10,activation='sigmoid')
])
# 超引數
batch_size = 128
learning_rate = 0.01
momentum=0.0
epoch=20
checkpoint = 20
# 訓練
def train_alexnet():
num_iter = dataLoader.num_train//batch_size
for e in range(epoch):
for n in range(num_iter):
x_batch, y_batch = dataLoader.get_batch_train(batch_size)
net.fit(x_batch, y_batch)
if n%checkpoint == 0:
net.save_weights("alexnet_weights.h5")
optimizer = tf.keras.optimizers.SGD(learning_rate=learning_rate, momentum=momentum, nesterov=False)
net.compile(optimizer=optimizer,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
train_alexnet()
# 載入並評估
net.load_weights("alexnet_weights.h5")
x_test, y_test = dataLoader.get_batch_test(2000)
net.evaluate(x_test, y_test, verbose=2)
執行中:

比較詳細的程式碼:
# -*- coding=UTF-8 -*-
import tensorflow as tf
# 輸入資料
import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# 定義網路超引數
learning_rate = 0.001
training_iters = 200000
batch_size = 64
display_step = 20
# 定義網路引數
n_input = 784 # 輸入的維度
n_classes = 10 # 標籤的維度
dropout = 0.8 # Dropout 的概率
# 預留位置輸入
x = tf.placeholder(tf.types.float32, [None, n_input])
y = tf.placeholder(tf.types.float32, [None, n_classes])
keep_prob = tf.placeholder(tf.types.float32)
# 折積操作
def conv2d(name, l_input, w, b):
return tf.nn.relu(tf.nn.bias_add( \
tf.nn.conv2d(l_input, w, strides=[1, 1, 1, 1], padding='SAME'),b) \
, name=name)
# 最大下取樣操作
def max_pool(name, l_input, k):
return tf.nn.max_pool(l_input, ksize=[1, k, k, 1], \
strides=[1, k, k, 1], padding='SAME', name=name)
# 歸一化操作
def norm(name, l_input, lsize=4):
return tf.nn.lrn(l_input, lsize, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name=name)
# 定義整個網路
def alex_net(_X, _weights, _biases, _dropout):
_X = tf.reshape(_X, shape=[-1, 28, 28, 1]) # 向量轉為矩陣
# 折積層
conv1 = conv2d('conv1', _X, _weights['wc1'], _biases['bc1'])
# 下取樣層
pool1 = max_pool('pool1', conv1, k=2)
# 歸一化層
norm1 = norm('norm1', pool1, lsize=4)
# Dropout
norm1 = tf.nn.dropout(norm1, _dropout)
# 折積
conv2 = conv2d('conv2', norm1, _weights['wc2'], _biases['bc2'])
# 下取樣
pool2 = max_pool('pool2', conv2, k=2)
# 歸一化
norm2 = norm('norm2', pool2, lsize=4)
# Dropout
norm2 = tf.nn.dropout(norm2, _dropout)
# 折積
conv3 = conv2d('conv3', norm2, _weights['wc3'], _biases['bc3'])
# 下取樣
pool3 = max_pool('pool3', conv3, k=2)
# 歸一化
norm3 = norm('norm3', pool3, lsize=4)
# Dropout
norm3 = tf.nn.dropout(norm3, _dropout)
# 全連線層,先把特徵圖轉為向量
dense1 = tf.reshape(norm3, [-1, _weights['wd1'].get_shape().as_list()[0]])
dense1 = tf.nn.relu(tf.matmul(dense1, _weights['wd1']) + _biases['bd1'], name='fc1')
# 全連線層
dense2 = tf.nn.relu(tf.matmul(dense1, _weights['wd2']) + _biases['bd2'], name='fc2')
# Relu activation
# 網路輸出層
out = tf.matmul(dense2, _weights['out']) + _biases['out']
return out
# 儲存所有的網路引數
weights = {
'wc1': tf.Variable(tf.random_normal([3, 3, 1, 64])),
'wc2': tf.Variable(tf.random_normal([3, 3, 64, 128])),
'wc3': tf.Variable(tf.random_normal([3, 3, 128, 256])),
'wd1': tf.Variable(tf.random_normal([4*4*256, 1024])),
'wd2': tf.Variable(tf.random_normal([1024, 1024])),
'out': tf.Variable(tf.random_normal([1024, 10]))
}
biases = {
'bc1': tf.Variable(tf.random_normal([64])),
'bc2': tf.Variable(tf.random_normal([128])),
'bc3': tf.Variable(tf.random_normal([256])),
'bd1': tf.Variable(tf.random_normal([1024])),
'bd2': tf.Variable(tf.random_normal([1024])),
'out': tf.Variable(tf.random_normal([n_classes]))
}
# 構建模型
pred = alex_net(x, weights, biases, keep_prob)
# 定義損失函數和學習步驟
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# 測試網路
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# 初始化所有的共用變數
init = tf.initialize_all_variables()
# 開啟一個訓練
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# 獲取批資料
sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys, keep_prob: dropout})
if step % display_step == 0:
# 計算精度
acc = sess.run(accuracy, feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.})
# 計算損失值
loss = sess.run(cost, feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.})
print "Iter " + str(step*batch_size) + ", Minibatch Loss= " + "{:.6f}".format(loss) + ", Training Accuracy= " + "{:.5f}".format(acc)
step += 1
print "Optimization Finished!"
# 計算測試精度
print "Testing Accuracy:", sess.run(accuracy, feed_dict={x: mnist.test.images[:256], y: mnist.test.labels[:256], keep_prob: 1.})
# 以上程式碼忽略了部分折積層,全連線層使用了特定的權重。
注:此來源於百度,僅供學習參考
參考文獻:
《ImageNet Classification with Deep Convolutional Neural Networks》
本文寫於2022年7月27日00:41