圖論的小技巧以及擴充套件
圖論,其實是數學的一門分支,它以圖為研究物件。最基礎的圖論應該是著名的哥尼斯堡七橋問題,那是一個經典的一筆畫問題。
競賽中我們比較常見的是 最短路演演算法 最小生成樹演演算法 拓撲排序 等等。
本篇文章我們不說那些大家都懂爛了的圖論演演算法,講一些實用的 (沒什麼用的) 圖論小技巧。
鏈式前向星存圖
最最基礎的存圖的基本分為兩種,使用二維陣列和使用 \(vector\) ,但這兩種方法都有所缺陷。
使用二維陣列查詢速度很快,但空間複雜度是 \(O(n^2)\) 的,一般的題目都接受不了。
使用 \(vector\) 可以減少空間複雜度,但是時間就比較不確定了。
所以就出現了一種神奇的存圖方式,連結串列思想的鏈式前向星。
我們通常使用以下陣列來完成
$Codes$
int w[i]//第 i 條邊的權值
int to[i]//第 i 條邊的終點
int nxt[i]//下一條的邊的編號,不建議叫 next,會掛
int head[i]//以 i 為起始點的第一條邊
int tot//邊的編號
新增加一條邊的時候我們進行如下操作
$Codes$
void add(int x,int y,int z){
tot++;//新邊的編號
to[tot]=y;//新一條邊的資訊
w[tot]=z;
nxt[tot]=head[x];
head[x]=tot;//更新以 x 為起始點的第一條邊
}
//這樣是單向邊,雙向邊要再來一次
用下面這種方式就可以列舉出所有以 xx 為起始點的邊。
$Codes$
for(int i=head[x];i;i=nxt[i]){// i 即為該邊編號
//to[i]為可以到達的點頭
//w[i]為這條邊的權值
}
大致思想就是將所有以 \(x\) 為起始點的邊以連結串列的形式儲存,列舉的時候遍歷連結串列,直到邊的編號為 \(0\) (為 \(0\) 表示沒有其他的邊了)
這樣就可以滿足我們從某個點遍歷列舉下個點的需要。
前向星連結串列被瘋狂應用在各個圖論題目中,基本上是一個圖論題都可以用到吧,屬於非常基礎的圖論技能。
需要注意的是對於雙向邊的題目,鏈式前向星的陣列需要開邊數的兩倍,不然會 \(RE\) 。
反向建邊
對於一個有向圖,某些問題中我們需要反向建邊來完成操作
比如求其他 \(n\) 個點到 \(k\) 點的最短路。
對每個點跑一遍最短路不就好了嗎?
事實上我們只需要跑一遍最短路就可以了,只需要把邊反向建。
反向建圖情況下 \(k\) 點到每個點的最短路就是正常情況下該點到 \(k\) 點的最短路。
例題 P1629 郵遞員送信
不只是最短路問題,在遍歷問題上也可以使用反向建邊來完成
例題 P3916 圖的遍歷
是否需要反向建邊,根據題意判斷即可。
反向建邊還可以來判斷某條邊是否在最短路上。
對於一個有向圖,我們從 11 號點跑一遍正向的最短路 \(dis[]\) ,從 \(n\) 號點跑一遍反向的最短路 \(dis1[]\)
如果 \(dis[x]+w(x,y)+dis1[y]=dis[n]\) 那麼我們就可以得出,這條邊是在 \(1\) 到 \(n\) 的最短路上的。
當然如果是無向圖的話直接跑就可以了。
虛點連邊
虛點連邊是一種很有效的優化建邊複雜度的方式
我們可能會遇見這樣一種題,給你幾個點,其他的點離這些給出的點的最近距離是多少。
我們可以對於每一個點進行 \(Spfa\),但似乎這樣並不是很好操作。
我們可以自己給出一個點,然後向每個被標記的點連一條單向邊,這樣就只需要進行一次 \(Spfa\) 就可以了。
舉個例子,橙色為標記點,數位為最近距離。
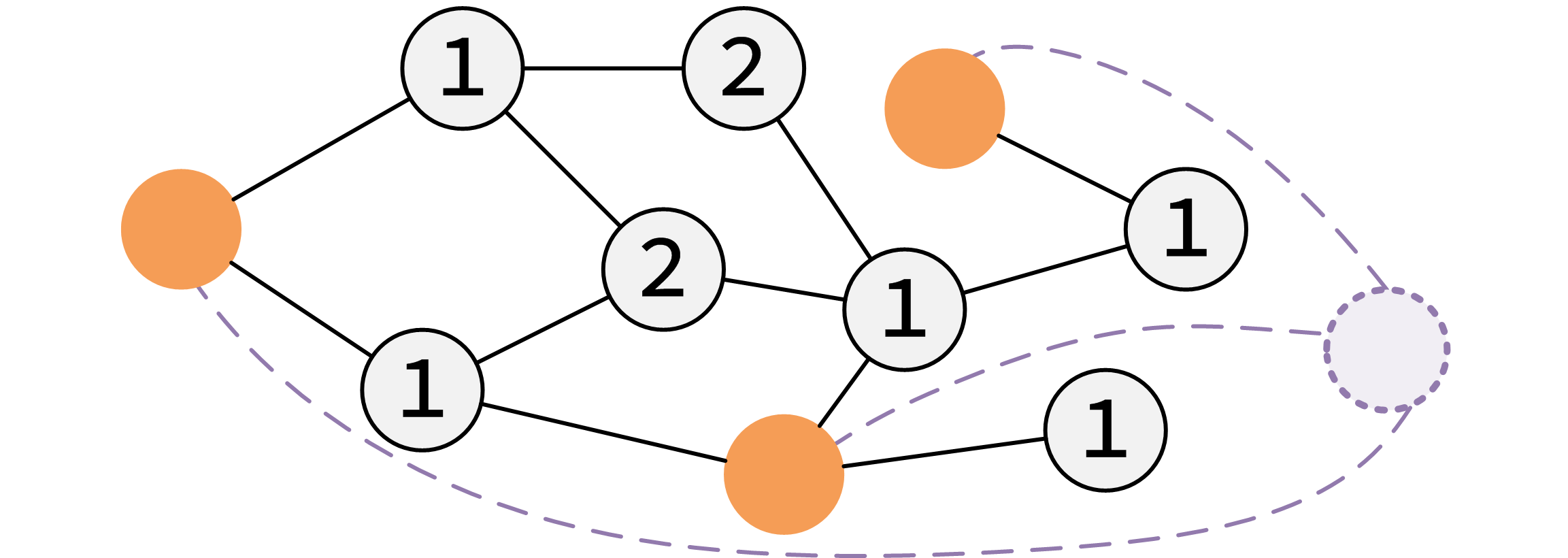
例題 P3393 逃離殭屍島
但似乎這個直接廣搜也可以。
如果對於兩個點集 \(A\) 和 \(B\),你需要對 \(A\) 中的每一個點向 \(B\) 中的每一個點都建一條邊,如果直接操作,複雜度很明顯是 \(O(n^2)\) 的,有沒有更快的方法呢?
我們可以建一個虛點 \(P\) ,然後對 \(A\) 裡的每一個點向 \(P\) 連一條單向邊邊,然後對 \(P\) 向 \(B\) 中的每一個點建一條單向邊,這樣只需要 \(O(2n)\) 的複雜度就可以完成了。
畫個圖理解一下。
(優化前)
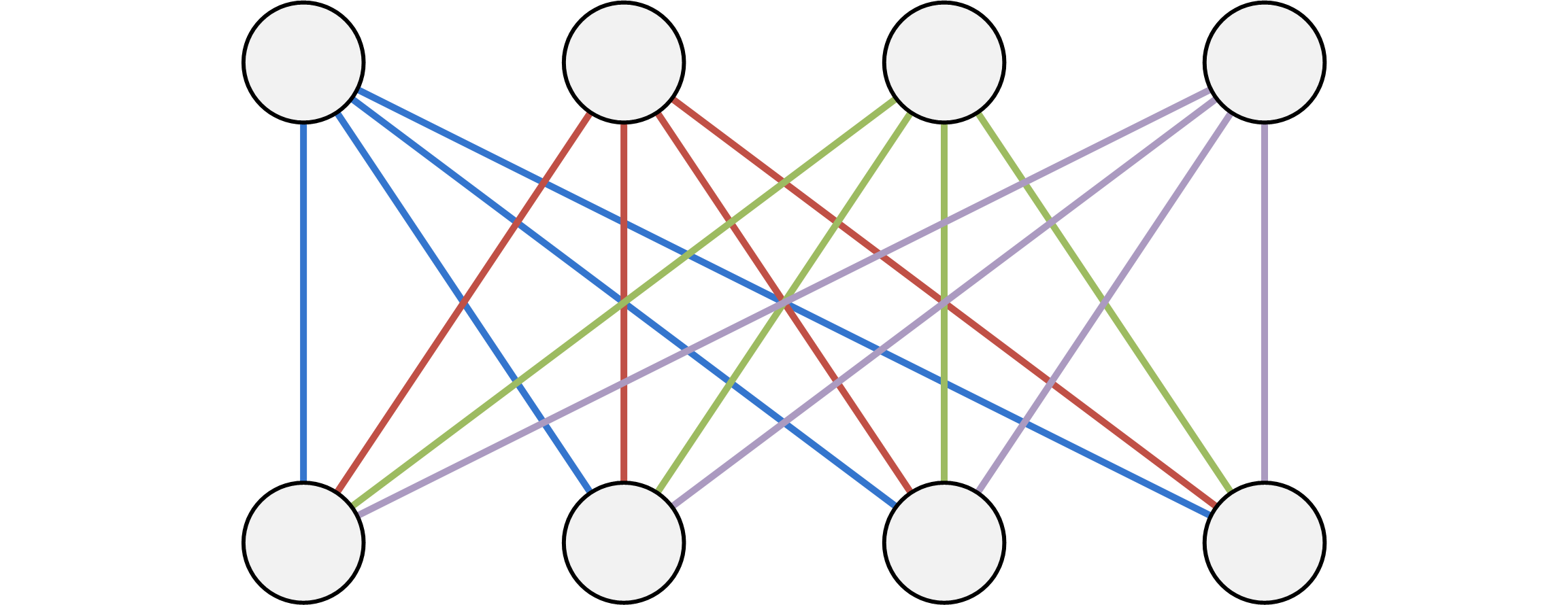
(優化後)
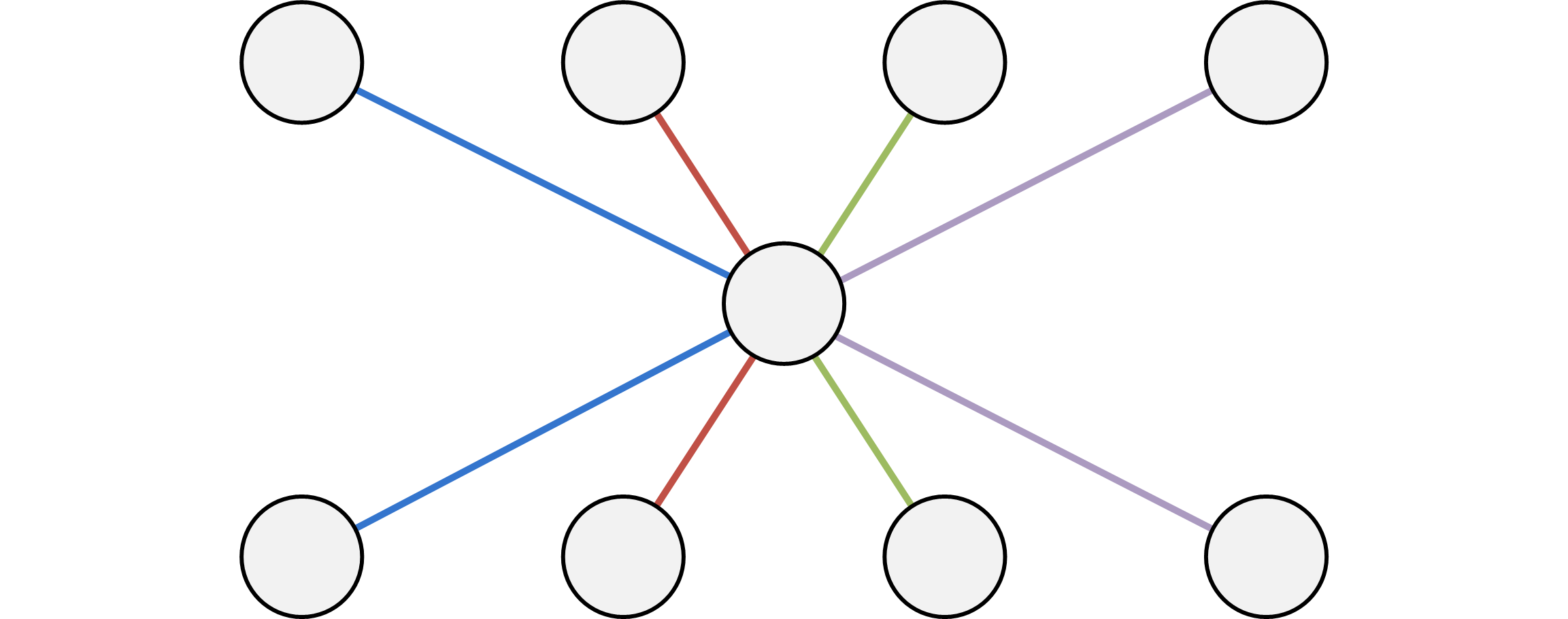
例題 P1983 車站分級
虛點連邊只是聽起來很高大上的操作,但實際上很簡單。
對於有邊權的情況,虛點連得邊的邊權需要注意(一般為 \(0\) )
線段樹優化建邊
說到優化建邊,就一定要介紹一下線段樹優化建邊了。
這也是一個聽起來非常高大上但實際上不是很難的技巧。
給你一個點 \(X\) ,讓你和一個點集裡的每一個點都連一條邊。看起來並沒有什麼好方法,只能乖乖地一個一個連
如果這個點集是連續的呢?我們就可以用線段樹來優化建邊了。
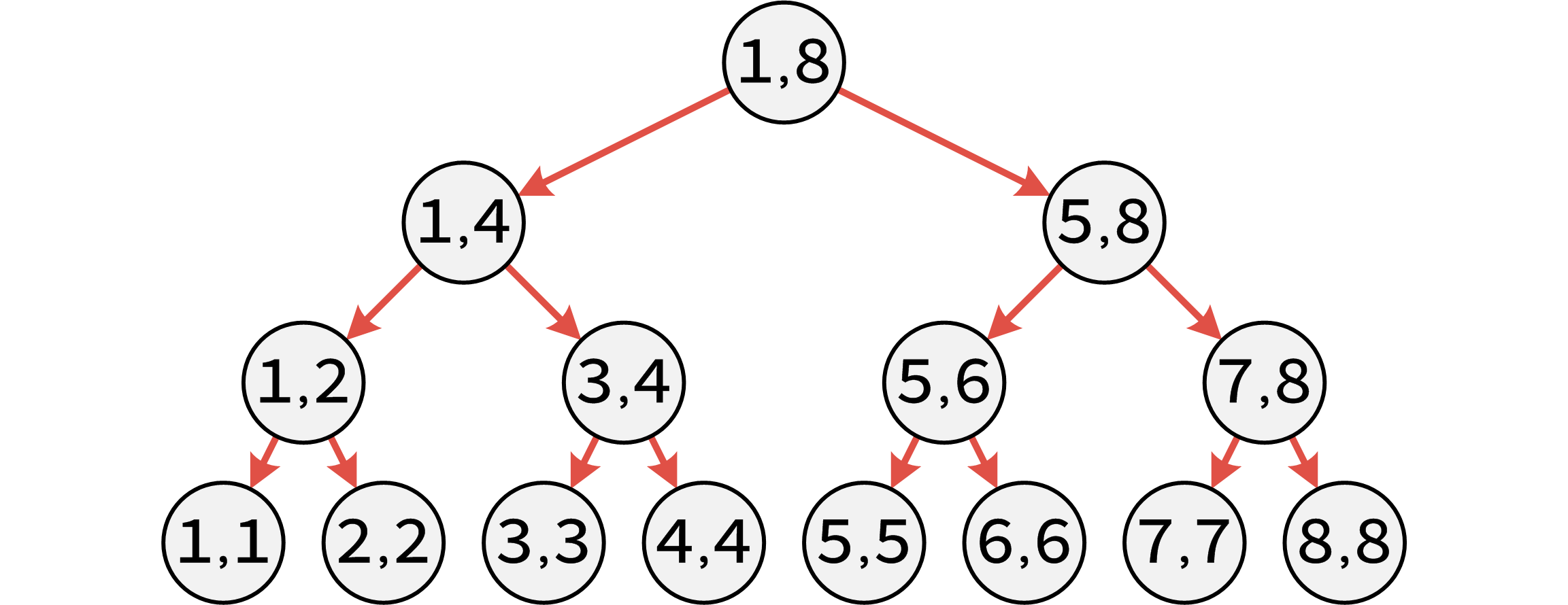
我們知道線段樹是這個結構的
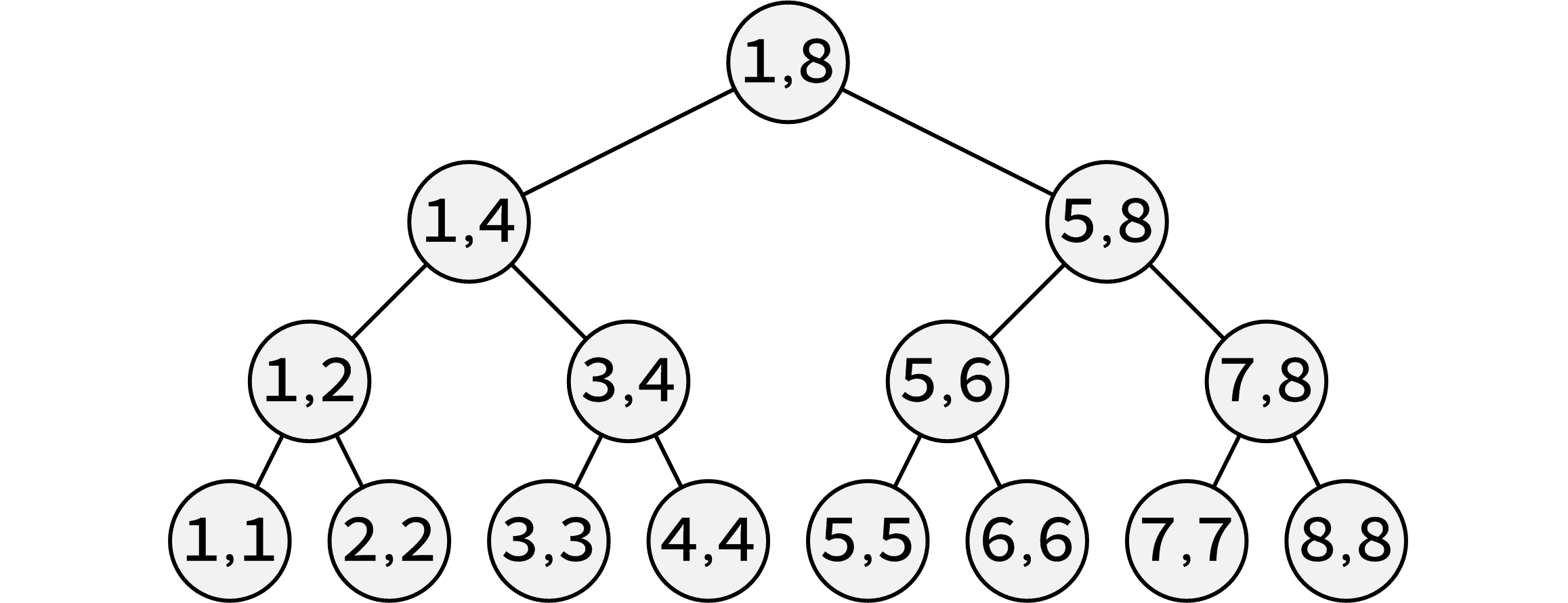
我們知道,線段樹的點是能夠代表一段區間的,那麼我們怎樣應用這個性質呢?
首先,我們需要對於線段樹的每個父親與他的兒子建一條單向邊,效果如下
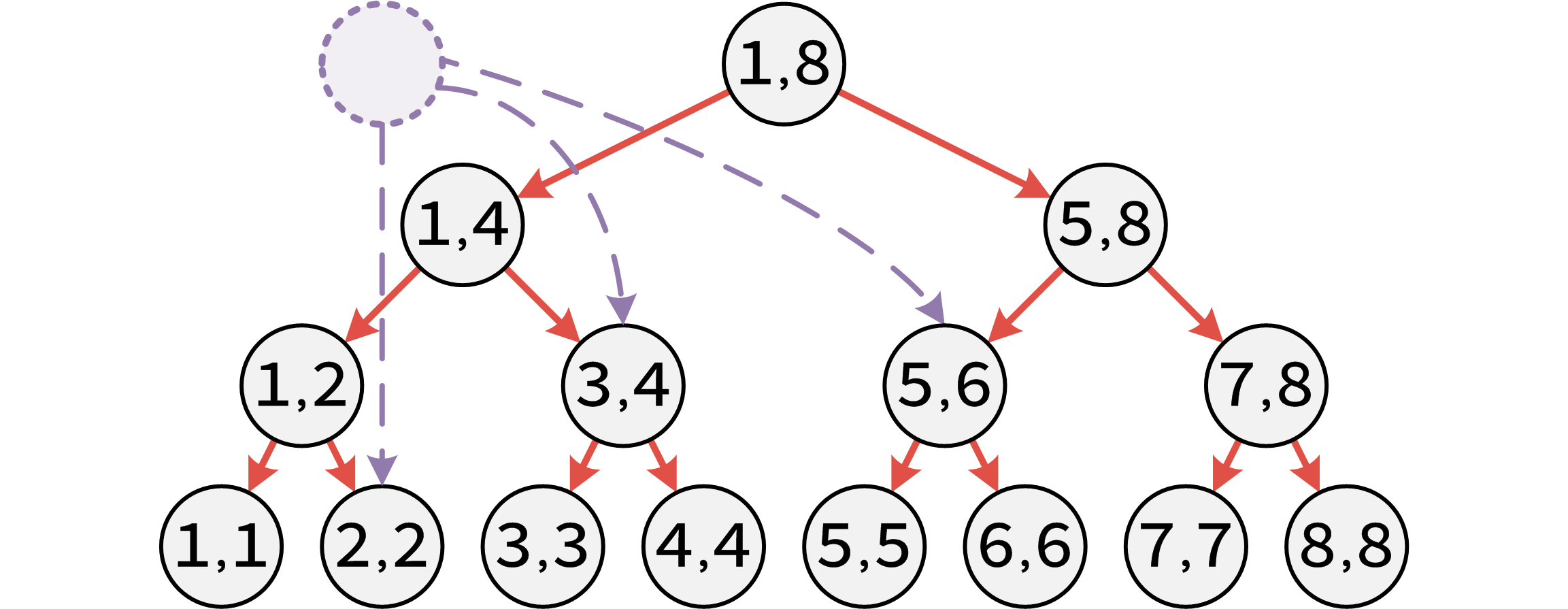
這有什麼用呢?因為我們所要求的點集是一段連續的區間,而線段樹的結點可以表示某一段區間,我們可以線上段樹上找到對應的區間,然後向線段樹上的點建邊,就可以加快建邊速度了。
例如我們要向 \([1,8]\) 裡的所有點建邊,我們只需要將 \(X\) 和線段樹上 \([1,8]\) 那個點連一條單向邊就可以了。
\([2,6]\) 的例子
我們線上段樹上的邊邊權一般都是 \(0\) ,邊權直接賦給 \(X\) 連到線段樹上的那條邊即可
建樹和尋找的程式碼和普通線段樹差不多。需要注意的是線段樹上結點的編號不要和已有的點重複,最後的結點直接連上該點就好。
$Codes$
void build(int &p,int l,int r){
if(l==r){
p=l;
return ;
}
p=++cnt;//點的編號
int mid=l+r>>1;
build(lc[p],l,mid);build(rc[p],mid+1,r);
add(lc[p],p,0);add(rc[p],p,0);
}
void update(int p,int l,int r,int x,int L,int R,int z){
if(L<=l && r<=R){
add(x,p,z);
return ;
}
int mid=l+r>>1;
if(L<=mid){
update(lc[p],l,mid,x,L,R,z);
}
if(R>mid) {
update(rc[p],mid+1,r,x,L,R,z);
}
}
這道題還涉及到了區間向某一個點連邊的情況,我們再建一個棵線段樹在樹上反向建邊就可以了
拆點構圖
有些時候我們並不能用一個點來代表一個點(霧)
誒我不是這個意思。我的意思是用幾個點來表示一個點的不同情況。
隨機口胡的一道題
一個圖,每條邊上有 \(k\) 個權值,第 \(i\) 次行走消耗的代價是第 \(i\%k+1\) 個權值,求某一個點的單源最短路徑。 \(( k\)很小\()\)
看起來直接跑 \(dij\) 和 \(spfa\) 是不對的,可以自舉反例。
可以使用 \(dfs\) ,用 \(dis[i][j]\) 表示到第 \(i\) 個點走了 \(m\) 步且 \(m\%k+1=j\) 的最短方案,但這樣太慢了。
我們可以使用拆點的思想,對於一個點 \(i\) ,將它拆為 \(i , i+n , i+2*n , ...\) 這樣的 \(k\) 個點,作為到這個點的步數模 \(k\) 不同情況的替代點。
然後我們連邊的時候對某一種情況賦不同情況的權值,大概下面這樣?
//我們要對 x 到 y 連三種邊 w1 w2 w3
add(x,y+n,w1);
add(x+n,y+2*n,w2);
add(x+2*n,y,w3);
來一張圖

然後在得到的圖上跑最短路就可以了,答案要列舉到終點的情況。
類似的例題 P4568 飛行路線
圖論建模
似乎……一些揹包問題可以用最短路解決,只是沒什麼必要。
\(Let us AC it--\)題面
\(Kodak\)開了一家小店賺外快,因為店小,所以只有 \(n\) 種不同價格的商品賣,不過好在批發商給力,貨源充足,所以每種商品都有無限件。
因為各種原因,有時候顧客會對購買的總價有特殊的要求,比如電腦科學家泰瑪仕一定要總價 \(1024\) ,給小姐姐買禮物的麵包需要總價 \(520\) 或者 \(1314\) ,或者純粹來找茬的張三要買\(0\)元商品
但是\(Kodak\)店裡不一定有 \(1\) 元的商品,所以並不是所有價格都湊得出來,所以他需要一個程式解決能知道某一個總價能否湊出
看起來可以用完全揹包解決這個問題,但是這道題的資料範圍不太友好。
商品數 \(N <= 1000\) \ 商品價格 \(a_i <= 20000\)
顧客數 \(M <= 300000\) \ 需求價格 \(b_i <= 40000000\)
如果打完全揹包,複雜度會爆炸。\(TAT\)
其實這個問題就是 \(a_1*x_1+a_2*x_2+a_3*x_3+...?=k\) 的問題。我們考慮 \(「\)同餘 \(+\) 最短路\(」\)
依題意得,如果 \(k\) 滿足要求,那麼 \(a_m*k\) 必定也滿足條件。我們可以先給它填一堆 \(a_m\) ,然後減去 \(p\) 個 \(a_m\) ,用剩下的 \(a_i\) 表示 \(p*a_m+k\%a_m\) 設當 \(b\%a_m=i\)時,需要的最小的 \(k×a_m+i\) 為 \(dis[i]\) ,剩下的即可用最短路的思想來更新,
跑最短路的過程基本如下
memset(dis,0x3f,sizeof(dis));
dis[0]=0;
q.push(0);
while(q.size()){
int x=q.top();
q.pop();
if(v[x]) continue;
v[x]=1;
for(int i=1;i<=n;i++){
int y=(x+a[i])%mod;
if(dis[y]>dis[x]+a[i]){
dis[y]=dis[x]+a[i];
q.push(y);
}
}
}
可能不是太好理解,結合樣例手推一下吧
又一道例題
給出 \(n\) 個 長度為 \(m\) 的 \(01\) 串,讓你確定一個長度相同的 \(01\) 串,該串和給出的串中不同的位數最多。
一道看起來跟圖論毫無關係的題,其實也可以當作圖論來做
我們可以建一個 \(2^m\) 的圖,每個點都與和自身不同位數為 \(1\) 的點連一條長度為 \(1\) 的邊,然後跑 \(bfs\),得到最遠距離的那個點即為所求。
廣搜程式碼
while(h<=t){
int x=v[h];
for(int i=1;i<=m;i++){
int z=x^(1<<(i-1));
if(f[z]==0){
f[z]=1;
t++;
v[t]=z;
dis[z]=dis[x]+1;
}
}
h++;
}
這有點類似於前面講的虛點連邊的那道題。
我講的可能比較菜,可以畫圖理解。
圖論中要注意的坑
簡單列述幾個小問題
\(1.\) 先看眼是有向圖還是無向圖,無向圖陣列開兩倍。
\(2.\) 如果題目中沒有宣告無自環和重邊,需要注意
\(3.\) 有些遍歷的題要考慮環,否則可能死迴圈,可以使用縮點
\(4.\) 如果題目中邊權小於等於零,要考慮負環、零環的情況
\(5.\) 跑最短路的時候要賦初值。
\(6.\) 關於 \(Spfa\) ,能不用還是不用吧,畢竟容易被卡。