詳細介紹JavaScript二元樹及各種遍歷演演算法

本篇文章給大家帶來了關於的相關知識，主要介紹了JavaScript二元樹及各種遍歷演演算法詳情，文章圍繞主題展開詳細的內容介紹，具有一定的參考價值，需要的小夥伴可以參考一下，希望對大家有幫助。

【相關推薦：、】

什麼是二元樹

二元樹是每個節點最多隻能有兩個子節點的樹，如下圖所示：

一個二元樹具有以下幾個特質：

第i層的節點最有隻有2^(i-1)個；
如果這顆二元樹的深度為k，那二元樹最多有2^k-1個節點；
在一個非空的二元樹中，若使用n0表示葉子節點的個數，n2是度為2的非葉子節點的個數，那麼兩者滿足關係n0 = n2 + 1。

滿二元樹

如果在一個二元樹中，除了葉子節點，其餘的節點的每個度都是2，則說明該二元樹是一個滿二元樹，

如下圖所示：

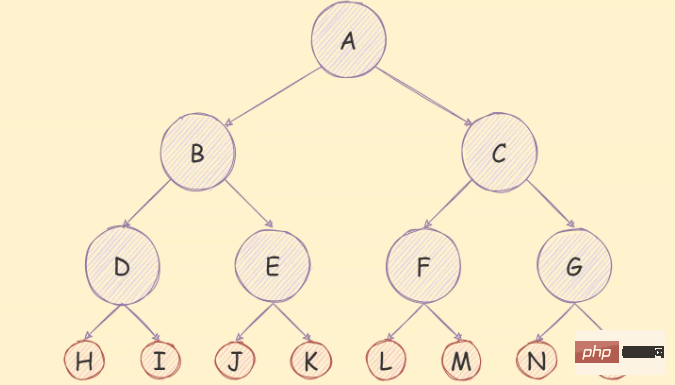
滿二元樹除了滿足普通二元樹特質，還具有如下幾個特質：

滿二元樹的的第n層具有2^(n-1)個節點；
深度為k的滿二元樹一定存在2^k-1個節點，葉子節點的個數為2^(k-1)；
具有n個節點的滿二元樹的深度為log_2^(n+1)。

完全二元樹

如果一個二元樹去掉最後一次層是滿二元樹，且最後一次的節點是依次從左到右分佈的，則這個二元樹是一個完全二元樹，

如下圖所示：

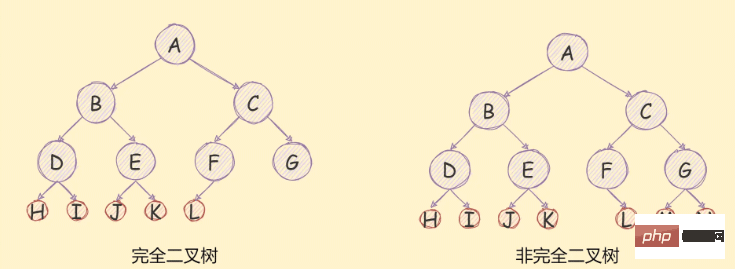
二元樹的儲存

儲存二元樹的常見方式分為兩種，一種是使用陣列儲存，另一種使用連結串列儲存。

陣列儲存

使用陣列儲存二元樹，如果遇到完全二元樹，儲存順序從上到下，從左到右，如下圖所示：

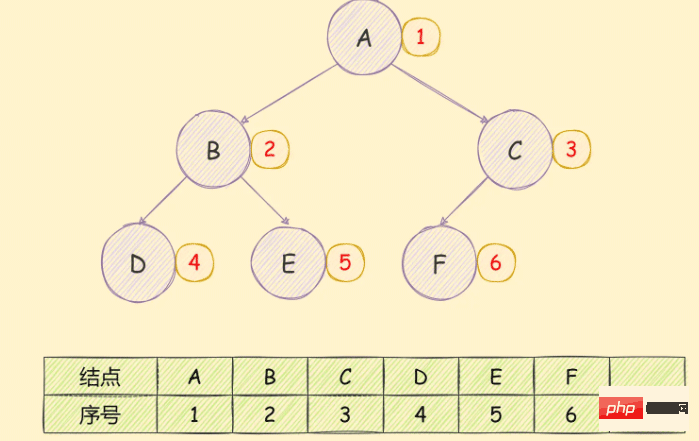
如果是一個非完全二元樹，如下圖所示：

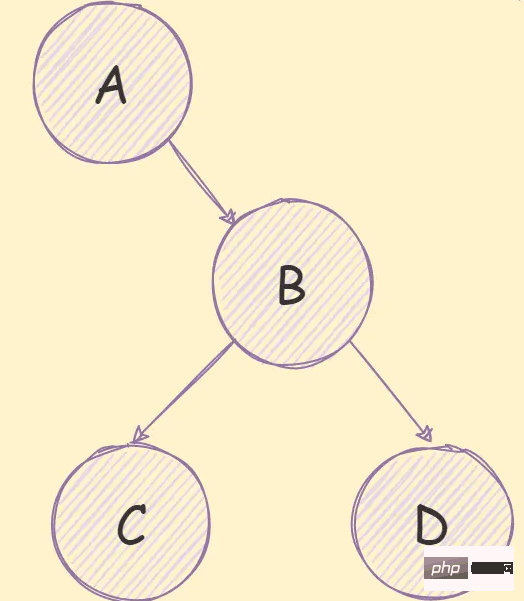
需要先將其轉換為完全二元樹，然後在進行儲存，如下圖所示：

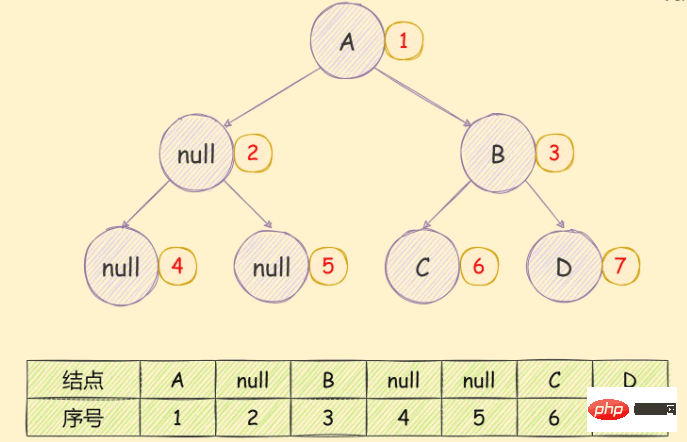
可以很明顯的看到儲存空間的浪費。

連結串列儲存

使用連結串列儲存通常將二元樹中的分為3個部分，如下圖：

這三個部分依次是左子樹的參照，該節點包含的資料，右子樹的參照，儲存方式如下圖所示：

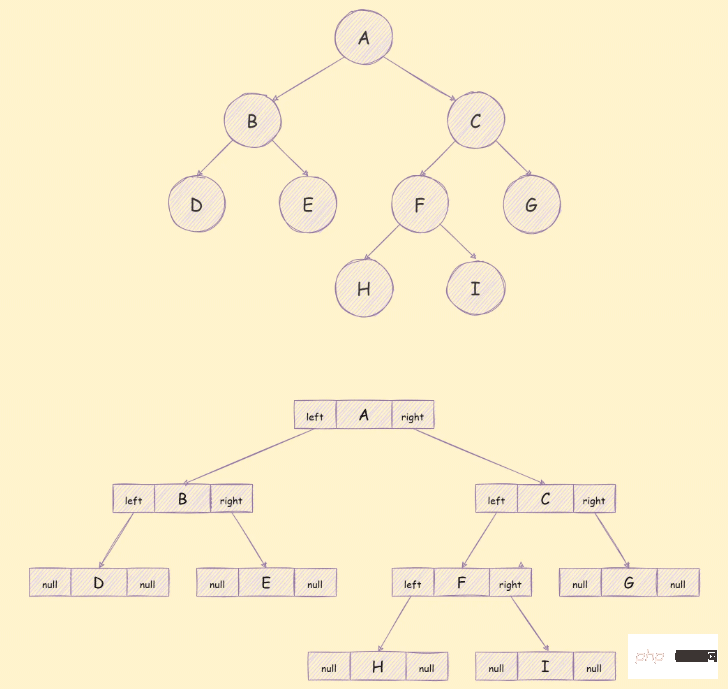
與二元樹相關的演演算法

以下演演算法中遍歷用到的樹如下：

// tree.js
const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}
module.exports = bt

深度優先遍歷

二元樹的深度優先遍歷與樹的深度優先遍歷思路一致，思路如下：

存取根節點；
存取根節點的left
存取根節點的right
重複執行第二三步

實現程式碼如下：

const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}

function dfs(root) {
  if (!root) return
  console.log(root.val)
  root.left && dfs(root.left)
  root.right && dfs(root.right) 
}
dfs(bt)
/** 結果
A B D E C F H I G
*/

廣度優先遍歷

實現思路如下：

建立佇列，把根節點入隊
把對頭出隊並存取
把隊頭的left和right依次入隊
重複執行2、3步，直到佇列為空

實現程式碼如下：

function bfs(root) {
  if (!root) return
  const queue = [root]
  while (queue.length) {
    const node = queue.shift()
    console.log(node.val)
    node.left && queue.push(node.left)
    node.right && queue.push(node.right)
  }
}
bfs(bt)
/** 結果
A B C D E F G H I
 */

先序遍歷

二元樹的先序遍歷實現思想如下：

存取根節點;
對當前節點的左子樹進行先序遍歷；
對當前節點的右子樹進行先序遍歷；

如下圖所示：

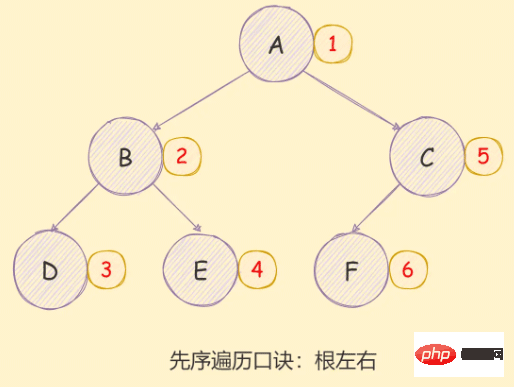
遞迴方式實現如下：

const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 結果
A B D E C F H I G
*/

迭代方式實現如下：

// 非遞迴版
function preorder(root) {
  if (!root) return
  // 定義一個棧，用於儲存資料
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由於棧存在先入後出的特性，所以需要先入右子樹才能保證先出左子樹 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 結果
A B D E C F H I G
*/

中序遍歷

二元樹的中序遍歷實現思想如下：

對當前節點的左子樹進行中序遍歷；
存取根節點;
對當前節點的右子樹進行中序遍歷；

如下圖所示：

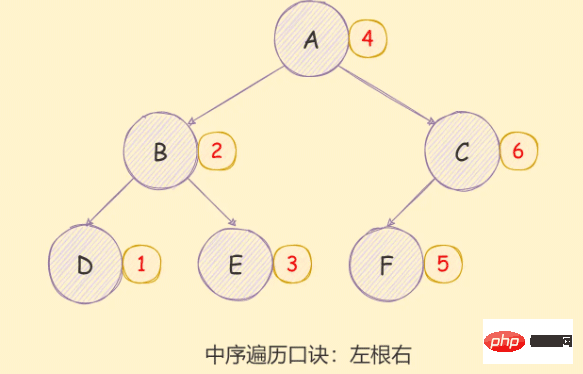
遞迴方式實現如下：

const bt = require('./tree')

// 遞迴版
function inorder(root) {
  if (!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}
inorder(bt)

/** 結果
D B E A H F I C G
*/

迭代方式實現如下：

// 非遞迴版
function inorder(root) {
  if (!root) return
  const stack = []
  // 定義一個指標
  let p = root
  // 如果棧中有資料或者p不是null，則繼續遍歷
  while (stack.length || p) {
    // 如果p存在則一致將p入棧並移動指標
    while (p) {
      // 將 p 入棧，並以移動指標
      stack.push(p)
      p = p.left
    }

    const node = stack.pop()
    console.log(node.val)
    p = node.right
  }
}
inorder(bt)
/** 結果
D B E A H F I C G
*/

後序遍歷

二元樹的後序遍歷實現思想如下：

對當前節點的左子樹進行後序遍歷；
對當前節點的右子樹進行後序遍歷；
存取根節點;

如下圖所示：

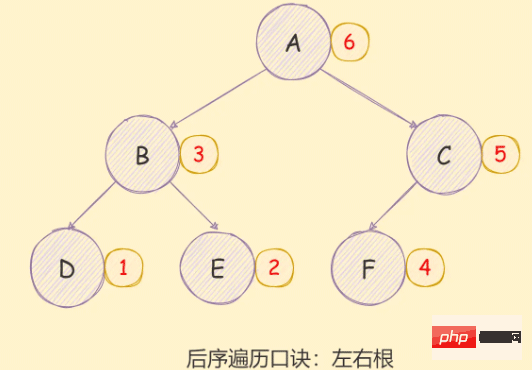
遞迴方式實現如下：

const bt = require('./tree')

// 遞迴版
function postorder(root) {
  if (!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}
postorder(bt)
/** 結果
D E B H I F G C A
*/

迭代方式實現如下：

// 非遞迴版
function postorder(root) {
  if (!root) return
  const outputStack = []
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    outputStack.push(node)
    // 這裡先入left需要保證left後出，在stack中後出，就是在outputStack棧中先出
    node.left && stack.push(node.left)
    node.right && stack.push(node.right)
  }
  while (outputStack.length) {
    const node = outputStack.pop()
    console.log(node.val)
  }
}
postorder(bt)
/** 結果
D E B H I F G C A
*/

【相關推薦：、】

以上就是詳細介紹JavaScript二元樹及各種遍歷演演算法的詳細內容，更多請關注TW511.COM其它相關文章！