四大經典演演算法思想
最經典的演演算法思想有以下幾種:
- 貪婪演演算法:每一步都採用最優的選擇,從而希望結果是最好的
- 分治演演算法:將原問題拆分成多個結果類似的子問題,遞迴解決後再合併其結果
- 回溯演演算法:類似於試探性列舉搜尋,用於指導深度優先搜尋這樣的經典演演算法
- 動態規劃:優化自頂向下的重複子問題,自底向上地推算出問題的最優解
貪婪演演算法
理論
貪婪演演算法是一種在每一步選擇當中都採取當前狀態下最好或最優(即最有利)的選擇,從而希望導致結果是最好或最優的演演算法。
貪婪演演算法在有最優子結構的問題中尤為有效,簡單地說,就是問題能夠分解成子問題來解決,子問題的最優解就能遞推到最終問題的最優解。
細節
- 建立數學模型來描述問題;
- 把問題分成若干個子問題;
- 對每一子問題求解,得到子問題的區域性最優解;
- 把子問題的區域性最優解合併成原來問題的一個解。
案例
對於零錢的問題:假設有 25 分、10 分、5 分、1 分這 4 種硬幣,現在要從中取出 41 分錢的硬幣,並且要求硬幣的個數最少。
通過貪婪演演算法,我們每次都拿出最大額度的硬幣,直到此額度超過了所需的額度。詳細的過程如下:
- 對於 41 分錢,拿出 25 分的硬幣,此時還差 16 分錢,25 分的硬幣超過了所需的額度,自然需要往更優、更小的額度去取;
- 對於 16 分錢,拿出 10 分的硬幣,此時還差 6 分錢,10 分的硬幣超過了所需的額度,自然需要往更優、更小的額度去取;
- 對於 6 分錢,拿出 5 分的硬幣,此時還差 1 分錢,5 分的硬幣超過了所需的額度,自然需要往更優、更小的額度去取;
- 對於 1 分錢,拿出 1 分的硬幣,此時還差 0 分錢;
- 最終,41 分錢拆分成了 1 個 25 分、1 個 10分、1 個 5 分、1 個 1 分,總共 4 個硬幣。
分治演演算法
理論
分治演演算法字面上的解釋是「分而治之」,就是把一個複雜的問題拆分成兩個或多個相同或相似的子問題,再把子問題拆分成更小的子問題......直到最後子問題可以簡單地求解,原問題的解即子問題的解的合併。
在廣義的定義下,所有遞迴或迴圈的演演算法均被視為「分治演演算法」,也有隻將具有最少兩個子問題的演演算法作為「分治演演算法」。
細節
在每一層遞迴上都有三個步驟:
- 分解:將原問題分解成若干個規模較小,相對獨立,與原問題形式相同的子問題;
- 解決:若子問題規模較小且易於解決時,則直接解。否則,遞迴地解決各子問題;
- 合併:將各子問題的解合併為原問題的解。
案例
分治演演算法最讓人熟知的應用案例就是歸併排序,以下歸併排序的部分程式碼能一一對應分治演演算法的細節步驟:
void merge_sort(int array[], unsigned int first, unsigned int last) {
int mid = 0;
if (first < last) {
mid = (first + last) / 2;
merge_sort(array, first, mid);
merge_sort(array, mid + 1,last);
merge(array,first,mid,last);
}
}
在 merge_sort() 函數中,將原本一個序列的排序問題從中間位置拆分成了兩個子序列的的排序問題:
- 對
first到mid的子序列排序; - 在對
mid+1到last的子序列排序; - 並且是遞迴呼叫
merge_sort()進行排序,最終將兩個有序子序列合併。
回溯演演算法
理論
回溯演演算法是一種擇優選擇的演演算法思想,又稱為試探法,按擇優條件向前搜尋,以達到目標。
將回溯演演算法對映到一個現實的例子就是:在迷宮當中,通過選擇不同的岔路口尋找出口,一個岔路口一個岔路口地去嘗試找到出口,如果在中途走錯了路,則返回到岔路口的另一條路,直到找到出口。
細節
用回溯演演算法解決問題的一般步驟:
- 針對所給問題,定義問題的解空間,它至少包含問題的一個(最優)解;
- 確定易於搜尋的解空間結構,使得能用回溯法方便地搜尋整個解空間;
- 以深度優先的方式搜尋解空間,並且在搜尋過程中用剪枝函數避免無效搜尋。
案例
在 8 x 8 的棋盤上,每一個空格可以放一個皇后,皇后可以攻擊與它同行、同列或同一斜線的其他皇后,在該棋盤上擺放 8 個皇后,使其不能互相攻擊。這就是「八皇后」問題,該問題就是典型的回溯演演算法案例,
對於一個 4 x 4 的棋盤結構,應該叫作「四皇后」問題,下述樹形結構是其解題思路:
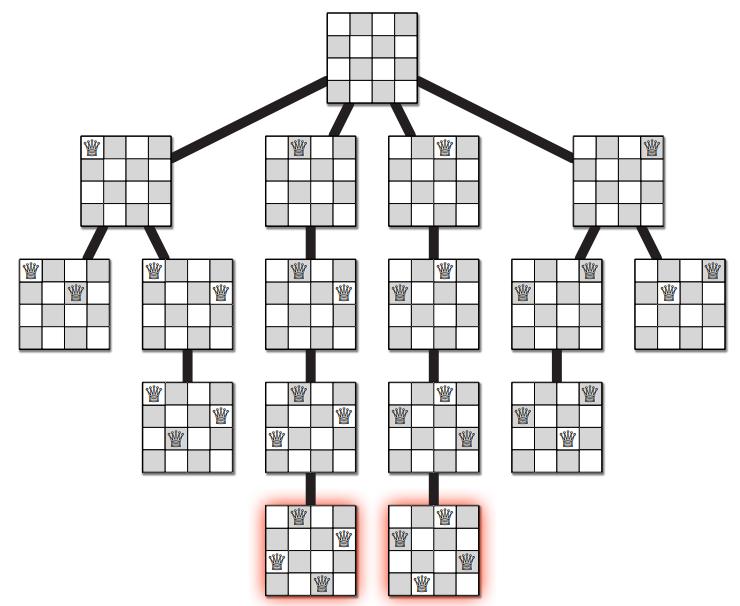
上圖就是一個回溯演演算法的思路,即先在第一行放置一個皇后,然後再試探性地再第二行放置一個皇后,以此類推,如果出現不滿足要求的情況,則及時止損,返回上一行繼續試探性地選擇不同的方案,直到所有的方案都被列舉出來位置。
這裡說的回溯演演算法有點像是窮舉法,其實它們是有點類似的,對於像「八皇后」問題需要所有解答時就可以將回溯演演算法認為是試探性窮舉法。
動態規劃
理論
動態規劃的思想是,若要解決一個給定問題,我們需要解其不同部分(即子問題),再根據子問題的解以得出原問題的解。
在各種場景中,動態規劃在對重複子問題求最優解時非常有效。其使用的方法是,在求解的過程中將子問題的結果儲存下來重複利用,從簡單的問題直到整個問題都被解決。
細節
使用動態規劃優化演演算法,基本上遵循一個固定的流程:
- 遞迴的暴力破解:將一個問題拆解成子問題,使用遞迴的思路解決問題;
- 帶備忘錄的遞迴解法:在遞迴的過程中,將子問題的結果儲存下來重複利用,減少時間耗費;
- 非遞迴的動態規劃解法:遵循自底向上的推算思路,將遞迴轉換成非遞迴的迴圈解法。
案例
如果想要求解斐波那契數列,使用遞迴的思路非常簡單,只要推算出遞迴的入口即可。
當想要優化的時候,也可以使用備忘錄儲存中間結果集,當然,對於求解斐波那契數列,此優化思路提升得並不多。
引入動態規劃的思路之後,自底向上求解斐波那契數列的思路就會有點與眾不同,如下是求解的程式碼:
int fib(int N) {
vector<int> dp(N + 1, 0);
dp[1] = dp[2] = 1;
for (int i = 3; i <= N; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[N];
}
其實,拿求解斐波那契數列的例子來說明並不能展現出動態規劃的優勢,但卻能展示出從一個遞迴演演算法改成動態規劃演演算法的過程。