作者：vivo 網際網路伺服器團隊-Tang Shutao

現如今推薦無處不在，例如抖音、淘寶、京東App均能見到推薦系統的身影，其背後涉及許多的技術。本文以經典的協同過濾為切入點，重點介紹了被工業界廣泛使用的矩陣分解演演算法，從理論與實踐兩個維度介紹了該演演算法的原理，通俗易懂，希望能夠給大家帶來一些啟發。筆者認為要徹底搞懂一篇論文，最好的方式就是動手復現它，復現的過程你會遇到各種各樣的疑惑、理論細節。

一、背景

1.1 引言

在資訊爆炸的二十一世紀，人們很容易淹沒在知識的海洋中，在該場景下搜尋引擎可以幫助我們迅速找到我們想要查詢的內容。在電商場景，如今的社會物質極大豐富，商品琳琅滿目，種類繁多。消費者很容易挑花眼，即使用者將會面臨資訊超載的問題。為了解決該問題，推薦引擎應運而生。例如我們開啟淘寶App，JD app，B站視訊app，每一個場景下都有推薦的模組。那麼此時有一個幼兒園小朋友突然問你，為什麼JD給你推薦這本《程式設計師頸椎康復指南》？你可能會回答，因為我的職業是程式設計師。接著小朋友又問，為什麼《Spark巨量資料分析》這本書排在第6個推薦位，而《Scala程式設計》排在第2位？這時你可能無法回答這個問題。

為了回答該問題，我們設想下面的場景：

在JD的電商系統中，存在著使用者和商品兩種角色，並且我們假設使用者都會對自己購買的商品打一個0-5之間的分數，分數越高代表越喜歡該商品。

基於此假設，我們將上面的問題轉化為使用者對《程式設計師頸椎康復指南》，《Spark巨量資料分析》，《Scala程式設計》這三本書打分的話，使用者會打多少分（使用者之前未購買過這3本書）。因此物品在頁面的先後順序就等價於預測使用者對這些物品的評分，並且根據這些評分進行排序的問題。

為了便於預測使用者對物品的評分問題，我們將所有三元組(User, Item, Rating)，即使用者User給自己購買的商品Item的評分為Rating，組織為如下的矩陣形式：

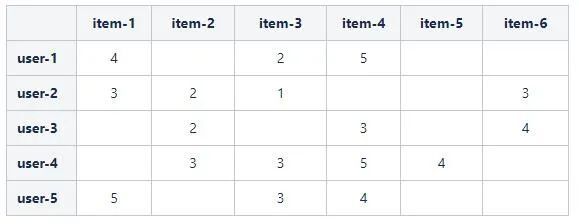
其中，表格包含\(m\)個使用者和\(n\)個物品，將表格定義為\({\bf{R}}_{m \times n}\)評分矩陣_，其中的元素\(r_{u,i})\)表示第\(u\)個使用者對第\(i\)個物品的評分。

例如，在上面的表格中，使用者user-1購買了物品 item-1， item-3， item-4，並且分別給出了4，2，5的評分。最終，我們將原問題轉化為預測白色空格處的數值。

1.2 協同過濾

協同過濾，簡單來說是利用與使用者興趣相投、擁有共同經驗之群體的喜好來推薦給使用者感興趣的物品。興趣相投使用數學語言來表達就是相似度 (人與人，物與物)。因此，根據相似度的物件，協同過濾可以分為基於使用者的協同過濾和基於物品的協同過濾。

以評分矩陣為例，以行方向觀測評分矩陣，每一行代表每個使用者的向量表示，例如使用者user-1的向量為 4, 0, 2, 5, 0, 0。以列方向觀測評分矩陣，每一列表示每個物品的向量表示，例如物品item-1的向量為4, 3, 0, 0, 5。

基於向量表示，相似度的計算有多種公式，例如餘弦相似度，歐氏距離，皮爾森。這裡我們以餘弦相似度為例，它是我們中學學過的向量夾角 (中學只涉及2維和3維) 的高維推廣，餘弦相似度公式很容易理解和使用。給定兩個向量\(\mathbf{A}=\{a_1, \cdots, a_n\}\)和\(\mathbf{B}=\{b_1, \cdots, b_n\}\)，其夾角定義如下：

\(\cos(\theta)=\frac{\bf{A}\cdot \bf{B}}{{|\bf{A}}|{|\bf{B}}|}=\frac{a_1 b_1 + \cdots + a_n b_n}{\sqrt{a_1^2+\cdots a_n^2}\sqrt{b_1^2 + \cdots b_n^2}}\)

例如，我們計算user-3和user-4的餘弦相似度，二者對應的向量分別為 0, 2, 0, 3, 0, 4，0, 3, 3, 5, 4, 0

\(\text{cos_sim}(u_3, u_4)=\frac{2 \times 3 + 3 \times 5}{\sqrt{2^2+3^2+4^2}\sqrt{3^2+3^2+5^2+4^2}} \approx 0.507685\)

向量夾角的餘弦值越接近1代表兩個物品方向越接近平行，也就是越相似，反之越接近-1代表兩個物品方向越接近反向，表示兩個物品相似度接近相反，接近0，表示向量接近垂直/正交，兩個物品幾乎無關聯。顯然，這和人的直覺完全一致。

例如，我們在視訊App中經常能看到"相關推薦"模組，其背後用到的原理之一就是相似度計算，下圖展示了一個具體的例子。

我們用《血族第一部》在向量庫 (儲存向量的資料庫，該系統能夠根據輸入向量，用相似度公式在庫中進行檢索，找出TopN的候選向量) 裡面進行相似度檢索，找到了前7部高相似度的影片，值得注意的是第一部是自己本身，相似度為1.0，其他三部是《血族》的其他3部同系列作品。

1.2.1 基於使用者的協同過濾 (UserCF)

基於使用者的協同過濾分為兩步

找出使用者相似度TopN的若干使用者。
根據TopN使用者評分的物品，形成候選物品集合，利用加權平均預估使用者u對每個候選物品的評分。

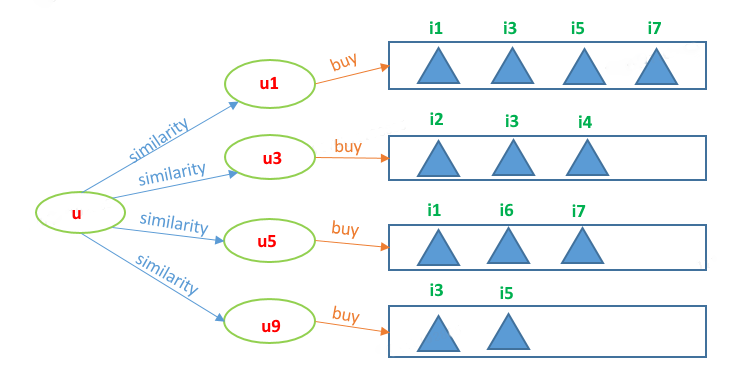
例如，由使用者u的相似使用者{u1, u3, u5, u9}可得候選物品為

\(\{i_1, i_2, i_3, i_4, i_5, i_6, i_7\}\)

我們現在預測使用者u對物品i1的評分，由於物品在兩個使用者{u1, u5}的購買記錄裡，因此使用者u對物品i1的預測評分為：

\({r}_{u,i_1} = \frac{\text{sim}{(u,u_1)}\times {r}_{u_1,i_1}+\text{sim}{(u,u_5)}\times {r}_{u_5,i_1}}{\text{sim}{(u,u_1)}+\text{sim}{(u,u_5)}}\)

其中\(\text{sim}{(u,u_1)}\)表示使用者\(u\)與使用者\(u_1\)的相似度。

在推薦時，根據使用者u對所有候選物品的預測分進行排序，取TopM的候選物品推薦給使用者u即可。

1.2.2 基於物品的協同過濾 (ItemCF)

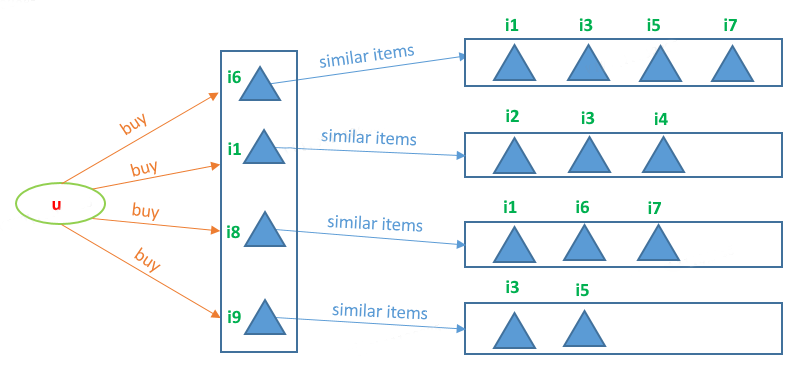
基於物品的協同過濾分為兩步：

在使用者u購買的物品集合中，選取與每一個物品TopN相似的物品。
TopN相似物品形成候選物品集合，利用加權平均預估使用者u對每個候選物品的評分。

例如，我們預測使用者u對物品i3的評分，由於物品i3與物品{i6, i1, i9}均相似，因此使用者u對物品i3的預測評分為：

\({r}_{u,i_3} = \frac{\text{sim}{(i_6,i_3)}\times {r}_{u,i_6}+\text{sim}{(i_1,i_3)}\times {r}_{u,i_1}+\text{sim}{(i_9,i_3)}\times {r}_{u,i_9}}{\text{sim}{(i_6,i_3)}+\text{sim}{(i_1,i_3)}+\text{sim}{(i_9,i_3)}}\)

其中\(\text{sim}{(i_6,i_3)}\)表示物品\(i_6\)與物品\(i_3\)的相似度，其他符號同理。

1.2.3 UserCF與ItemCF的比較

我們對ItemCF和UserCF做如下總結：

UserCF主要用於給使用者推薦那些與之有共同興趣愛好的使用者喜歡的物品，其推薦結果著重於反映和使用者興趣相似的小群體的熱點，更社會化一些，反映了使用者所在的小型興趣群體中物品的熱門程度。在實際應用中，UserCF通常被應用於用於新聞推薦。ItemCF給使用者推薦那些和他之前喜歡的物品類似的物品，即ItemCF的推薦結果著重於維繫使用者的歷史興趣，推薦更加個性化，反應使用者自己的興趣。在實際應用中，圖書、電影平臺使用ItemCF，比如豆瓣、亞馬遜、Netflix等。除了基於使用者和基於物品的協同過濾，還有一類基於模型的協同過濾演演算法，如上圖所示。此外基於使用者和基於物品的協同過濾又可以歸類為基於鄰域 (K-Nearest Neighbor, KNN) 的演演算法，本質都是在找"TopN鄰居"，然後利用鄰居和相似度進行預測。

二、矩陣分解

經典的協同過濾演演算法本身存在一些缺點，其中最明顯的就是稀疏性問題。我們知道評分矩陣是一個大型稀疏矩陣，導致在計算相似度時，兩個向量的點積等於0 (以餘弦相似度為例)。為了更直觀的理解這一點，我們舉例如下：

我們從評分矩陣中抽取item1 - item4的向量，並且利用餘弦相似度計算它們之間的相似度

rom sklearn.metrics.pairwise import cosine_similarity
 
a = [
  [  0,   0,   0,   3,   2,  0, 3.5,  0,  1 ],
  [  0,   1,   0,   0,   0,  0,   0,  0,  0 ],
  [  0,   0,   1,   0,   0,  0,   0,  0,  0 ],
  [4.1, 3.8, 4.6, 3.8, 4.4,  3,   4,  0, 3.6]
]
 
cosine_similarity(a)
 
# array([[1.        , 0.        , 0.        , 0.66209271],
#        [0.        , 1.        , 0.        , 0.34101639],
#        [0.        , 0.        , 1.        , 0.41280932],
#        [0.66209271, 0.34101639, 0.41280932, 1.        ]])

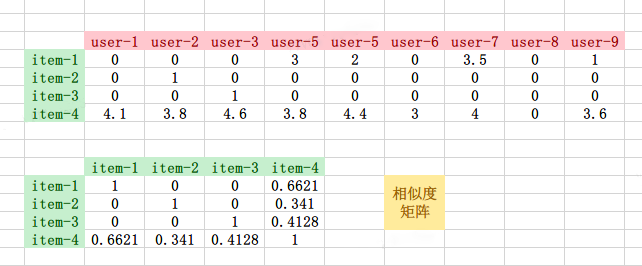
我們從評分矩陣中抽取item1 - item4的向量，並且利用餘弦相似度計算它們之間的相似度。

通過相似度矩陣，我們可以看到物品item-1, item-2, item-3的之間的相似度均為0，而且與item-1, item-2, item-3最相似的物品都是item-4，因此在以ItemCF為基礎的推薦場景中item-4將會被推薦給使用者。

但是，物品item-4與物品item-1, item-2, item-3最相似的原因是item-4是一件熱門商品，購買的使用者多，而物品item-1, item-2, item-3的相似度均為0的原因僅僅是它們的特徵向量非常稀疏，缺乏相似度計算的直接資料。

綜上，我們可以看到經典的基於使用者/物品的協同過濾演演算法有天然的缺陷，無法處理稀疏場景。為了解決該問題，矩陣分解被提出。

2.1 顯示反饋

我們將使用者對物品的評分行為定義為顯示反饋。基於顯示反饋的矩陣分解是將評分矩陣\({\bf{R}}_{m \times n}\)用兩個矩陣\({\bf{X}}_{m \times k}\)和\({\bf{Y}}_{n \times k}\)的乘積近似表示，其數學表示如下：

\({\bf{R}}_{m \times n} \approx {\bf{X}}_{m \times k}\left({\bf{Y}}_{n \times k}\right)^{\text T}\)

其中，\(k \ll m/n\)表示隱性因子，以使用者側來理解，\(k=2\)表示的就是使用者的年齡和性別兩個屬性。此外有個很好的比喻就是物理學的三稜鏡，白光在三稜鏡的作用下被分解為7種顏色的光，在矩陣分解演演算法中，分解的作用就類似於"三稜鏡"，如下圖所示，因此，矩陣分解也被稱為隱語意模型。矩陣分解將系統的自由度從\(\mathcal{O}(mn)\)降到了\(\mathcal{O}((m+n)k)\)，從而實現了降維的目的。

為了求解矩陣\({\bf{X}}_{m \times k}\)和\({\bf{Y}}_{n \times k}\)，需要最小化平方誤差損失函數，來儘可能地使得兩個矩陣的乘積逼近評分矩陣\({\bf{R}}_{m \times n}\)，即

\(\min\limits_{{\bf{x}}^*,{\bf{y}}^*} L({\bf{X}},{\bf{Y}})=\min\limits_{{\bf{x}}^*,{\bf{y}}^*}\sum\limits_{r_{u,i} \text{ is known}}(r_{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i)^2+\lambda \left( \sum\limits_{u}{\bf{x}}_u^{\text T}{\bf{x}}_u+\sum\limits_{i}{\bf{y}}_i^{\text T}{\bf{y}}_i\right)\)

其中，\(\lambda \left( \sum\limits_{u}{\bf{x}}_u^{\text T}{\bf{x}}_u+\sum\limits_{i}{\bf{y}}_i^{\text T}{\bf{y}}_i\right)\)為懲罰項，\(\lambda\)為懲罰係數/正則化係數，\(\mathbf{x}_u\)表示第\(u\)個使用者的\(k\)維特徵向量，\(\mathbf{y}_i\)表示第\(i\)個物品的\(k\)維特徵向量。

\({\bf{x}}_u = \begin{pmatrix} x_{u,1} \ \vdots \ x_{u,k} \ \end{pmatrix} \qquad {\bf{y}}_i = \begin{pmatrix} y_{i,1} \ \vdots \ y_{i,k} \ \end{pmatrix}\)

全體使用者的特徵向量構成了使用者矩陣\({\bf{X}}_{m \times k}\)_，全體物品的特徵向量構成了物品矩陣\({\bf{Y}}_{n \times k}\)。

\({\bf{X}}_{m \times k}= \begin{pmatrix} {\bf{x}}_{1}^{\text T} \ \vdots \ {\bf{x}}_{m}^{\text T} \ \end{pmatrix} \qquad {\bf{Y}}_{n \times k}= \begin{pmatrix} {\bf{y}}_{1}^{\text T} \ \vdots \ {\bf{y}}_{n}^{\text T} \ \end{pmatrix}\)

我們訓練模型的時候，就只需要訓練使用者矩陣中的\(m \times k\)引數和物品矩陣中的\(n \times k\)個引數。因此，協同過濾就成功轉化成了一個優化問題。

2.2 預測評分

通過模型訓練 (即求解模型係數的過程)，我們得到使用者矩陣\({\bf{X}}_{m \times k}\)和物品矩陣\({\bf{Y}}_{n \times k}\)，全部使用者對全部物品的評分預測可以通過\({\bf{X}}_{m \times k}\left({\bf{Y}}_{n \times k}\right)^{\text T}\)獲得。如下圖所示。

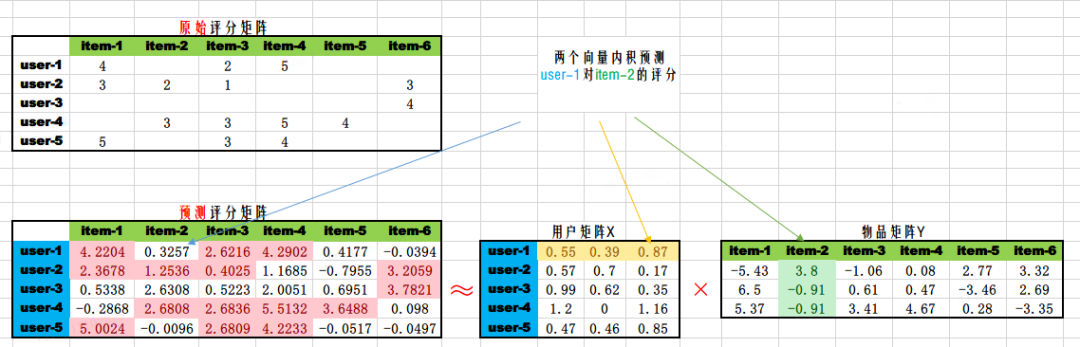
得到全部的評分預測後，我們就可以對每個物品進行擇優推薦。需要注意的是，使用者矩陣和物品矩陣的乘積，得到的評分預估值，與使用者的實際評分不是全等關係，而是近似相等的關係。如上圖中兩個矩陣粉色部分，使用者實際評分和預估評分都是近似的，有一定的誤差。

2.3 理論推導

矩陣分解ALS的理論推導網上也有不少，但是很多推導不是那麼嚴謹，在操作向量導數時有的步驟甚至是錯誤的。有的博主對損失函數的求和項理解出現錯誤，例如

\(\sum\limits_{\color{red}{u=1}}^{\color{red} m}\sum\limits_{\color{red}{i=1}}^{\color{red} n}(r_{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i)^2\)

但是評分矩陣是稀疏的，求和並不會貫穿整個使用者集和物品集。正確的寫法應該是

\(\sum\limits_{\color{red}{(u,i) \text{ is known}}}(r_{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i)^2\)

其中，\({(u,i) \text{ is known}}\)表示已知的評分項。

我們在本節給出詳細的、正確的推導過程，一是當做數學小練習，其次也是對演演算法有更深層的理解，便於閱讀Spark ALS的原始碼。

將\({(u,i) \text{ is known}}\)使用數學語言描述，矩陣分解的損失函數定義如下：

\(L({\bf{X}},{\bf{Y}})=\sum\limits_{\color{red}{(u,i) \in K}}(r_{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i)^2+\lambda \left( \sum\limits_{u}{\bf{x}}_u^{\text T}{\bf{x}}_u+\sum\limits_{i}{\bf{y}}_i^{\text T}{\bf{y}}_i\right)\)

其中\(K\)為評分矩陣中已知的\((u, i)\)集合。例如下面的評分矩陣對應的\(K\)為

\({\bf{R}}_{4 \times 4} = \begin{pmatrix} 0 & r{1,2} & r{1,3} & 0 \ r{2,1} & 0 & r{2,3} & 0 \ 0 & r{3,2} & 0 & r{3,4} \ 0 & r{4,2} & r{4,3} & r_{4,4} \end{pmatrix} \ \Rightarrow \color{red}{K = {(1,2), (1,3), (2,1), (2,3), (3,2), (3,4), (4,2), (4,3), (4,4)}}\)

求解上述損失函數存在兩種典型的優化方法，分別為

交替最小二乘 (Alternating Least Squares, ALS)
隨機梯度下降 (Stochastic Gradient Descent, SGD)

交替最小二乘，指的是固定其中一個變數，利用最小二乘求解另一個變數，以此交替進行，直至收斂或者到達最大迭代次數，這也是「交替」一詞的由來。

隨機梯度下降，是優化理論中最常用的一種方式，通過計算梯度，然後更新待求的變數。

在矩陣分解演演算法中，Spark最終選擇了ALS作為官方的唯一實現，原因是ALS很容易實現並行化，任務之間沒有依賴。

下面我們動手推導一下整個計算過程，在機器學習理論中，微分的單位一般在向量維度，很少去對向量的分量為偏微分推導。

首先我們固定物品矩陣\({\bf{Y}}\)，將物品矩陣\({\bf{Y}}\)看成常數。不失一般性，我們定義使用者\(u\)評分過的物品集合為\(I_u\)，利用損失函數對向量\(\mathbf{x}_u\)求偏導，並且令導數等於0可得：

\(\displaystyle \frac{\partial L}{\partial {\bf{x}}u}=-2\sum\limits{i \in Iu}(r{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i)\frac{\partial {(\bf{x}}_u^{\text T}{\bf{y}}_i)}{\partial {\bf{x}}_u}+2\lambda \frac{\partial {(\bf{x}}_u^{\text T}{\bf{x}}_u)}{\partial {\bf{x}}_u}=0, \quad u=1, \cdots, m \ \begin{split} & \quad \Rightarrow \sum\limits{i \in I_u}(r{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i){\bf{y}}_i^{\text T}=\lambda {\bf{x}}_u^{\text T} \ & \quad \Rightarrow \sum\limits{i \in I_u}r{u,i}{\bf{y}}i^{\text T}-\sum\limits{i \in I_u}{\bf{x}}_u^{\text T}{\bf{y}}_i{\bf{y}}_i^{\text T}=\lambda {\bf{x}}_u^{\text T} \ & \quad \Rightarrow \sum\limits{i \in I_u}{\bf{x}}_u^{\text T}{\bf{y}}_i{\bf{y}}_i^{\text T}+\lambda {\bf{x}}_u^{\text T}=\sum\limits{i \in Iu}r{u,i}{\bf{y}}_i^{\text T} \end{split}\)

因為向量\(\mathbf{x}_u\)與求和符號\(\sum\limits_{i \in I_u}\)無關，所有將其移出求和符號，因為\({\bf{x}}_u^{\text T}{\bf{y}}_i{\bf{y}}_i^{\text T}\)是矩陣相乘 (不滿足交換性)，因此\(\mathbf{x}_u\)在左邊\(\begin{split} & {\bf{x}}u^{\text T}\sum\limits{i \in Iu}{\bf{y}}_i{\bf{y}}_i^{\text T}+\lambda {\bf{x}}_u^{\text T}=\sum\limits{i \in Iu}r{u,i}{\bf{y}}_i^{\text T} \ \end{split}\) 等式兩邊取轉置，我們有

\(\begin{split} & \quad \Rightarrow \left({\bf{x}}u^{\text T}\sum\limits{i \in Iu}{\bf{y}}_i{\bf{y}}_i^{\text T}+\lambda {\bf{x}}_u^{\text T}\right)^{\text T}=\left(\sum\limits{i \in Iu}r{u,i}{\bf{y}}_i^{\text T}\right)^{\text T} \ & \quad \Rightarrow \left(\sum\limits{i \in I_u}{\bf{y}}_i{\bf{y}}_i^{\text T}\right){\bf{x}}_u+\lambda {\bf{x}}_u=\sum\limits{i \in Iu}r{u,i}{\bf{y}}_i \ & \quad \Rightarrow \left(\sum\limits{i \in I_u}{\bf{y}}_i{\bf{y}}_i^{\text T}+\lambda {\bf{I}}_k\right){\bf{x}}_u=\sum\limits{i \in Iu}r{u,i}{\bf{y}}_i \end{split}\)

為了化簡\(\sum\limits_{i \in I_u}{\bf{y}}_i{\bf{y}}_i^{\text T}\)與\(\sum\limits_{i \in I_u}r_{u,i}{\bf{y}}_i\)，我們將\(I_u\)展開。

假設\(I_u=\{i_{c_1}, \cdots, i_{c_N}\}\), 其中\(N\)表示使用者\(u\)評分過的物品數量，\(i_{c_i}\)表示第\(c_i\)個物品對應的索引/序號，藉助於\(I_u\)，我們有

\(\sum\limits_{i \in I_u}{\bf{y}}_i{\bf{y}}_i^{\text T}= \begin{pmatrix} {\bf{y}}_{c_1}, \cdots,{\bf{y}}_{c_N} \end{pmatrix} \begin{pmatrix} {\bf{y}}_{c_1}^{\text T} \\ \vdots \\{\bf{y}}_{c_N}^{\text T} \end{pmatrix}={\bf{Y}}_{I_u}^{\text T}{\bf{Y}}_{I_u} \\ \sum\limits_{i \in I_u}r_{u,i}{\bf{y}}_i= \begin{pmatrix}{\bf{y}}_{c_1}, \cdots,{\bf{y}}_{c_N} \end{pmatrix} \begin{pmatrix} r_{u,c_1} \\ \vdots \\ r_{u,c_N} \end{pmatrix}={\bf{Y}}_{I_u}^{\text T}{\bf{R}}_{u,I_u}^{\text T}\)

其中，\({\bf{Y}}_{I_u}\)為以\(I_u=\{i_{c_1}, \cdots i_{c_N}\}\)為行號在物品矩陣\({\bf{Y}}\)中選取的\(N\)個行向量形成的子矩陣

\({\bf{R}}_{u,I_u}\)為以\(I_u=\{i_{c_1}, \cdots i_{c_N}\}\)為索引，在評分矩陣\({\bf{R}}\)的第\(u\)行的行向量中選取的\(N\)個元素，形成的子行向量

因此，我們有

\(\left({\bf{Y}}{I_u}^{\text T}{\bf{Y}}{Iu}+\lambda {\bf{I}}_k\right){\bf{x}}_u={\bf{Y}}{Iu}^{\text T}{\bf{R}}{u,I_u}^{\text T} \ \quad \Rightarrow {\bf{x}}u=\left({\bf{Y}}{Iu}^{\text T}{\bf{Y}}{Iu}+\lambda {\bf{I}}_k\right)^{-1}{\bf{Y}}{Iu}^{\text T}{\bf{R}}{u,I_u}^{\text T}\)

網上的部落格，許多博主給出類似下面形式的結論不是很嚴謹，主要是損失函數的理解不到位導致的。

\({\bf{x}}_u=\left({\bf{\color{red} Y}}^{\text T}{\bf{\color{red} Y}}+\lambda {\bf{I}}_k\right)^{-1}{\bf{\color{red} Y}}^{\text T}{\bf{\color{red} R}}_{u}^{\text T}\)

同理，我們定義物品\(i\)被評分的使用者集合為\(U_i=\{u_{d_1}, \cdots u_{d_M}\}\)

根據對稱性可得

\({\bf{y}}_i=\left({\bf{X}}_{U_i}^{\text T}{\bf{X}}_{U_i}+\lambda {\bf{I}}_k\right)^{-1}{\bf{X}}_{U_i}^{\text T}{\bf{R}}_{i,U_i}\)

其中，\({\bf{X}}_{U_i}\)為以\(U_i=\{u_{d_1}, \cdots, u_{d_M}\}\)為行號在使用者矩陣\({\bf{X}}\)中選取的\(M\)個行向量形成的子矩陣

\({\bf{R}}_{i,U_i}\)為以\(U_i=\{u_{d_1}, \cdots, u_{d_M}\}\)為索引，在評分矩陣\({\bf{R}}\)的第\(i\)列的列向量中選取的\(M\)個元素，形成的子列向量

此外，\(\mathbf{I}_k\)為單位矩陣

如果讀者感覺上述的推導還是很抽象，我們也給一個具體範例來體會一下中間過程

\(\begin{pmatrix} 0 & r_{1,2} & r_{1,3} & 0 \\ r_{2,1} & 0 & r_{2,3} & 0 \\ 0 & r_{3,2} & 0 & r_{1,3} \\ 0 & r_{2,2} & r_{2,3} & r_{2,4} \\ \end{pmatrix} \approx \begin{pmatrix} x_{1,1} & x_{1,2} \\ x_{2,1} & x_{2,2} \\ x_{3,1} & x_{3,2} \\ x_{4,1} & x_{4,2} \end{pmatrix} \begin{pmatrix} y_{1,1} & y_{1,2} \\ y_{2,1} & y_{2,2} \\ y_{3,1} & y_{3,2} \\ y_{4,1} & y_{4,2} \end{pmatrix}^{\text T} \\ \Rightarrow {\bf{R}} \approx {\bf{X}} {\bf{Y}}^{\text T}\)

注意到損失函數是一個標量，這裡我們只展開涉及到\(x_{1,1}, x_{1,2}\)的項，如下所示

\(\sum\limits_{\color{red}{(u,i) \text{ is known}}}(r_{u,i} - {\bf{x}}_u^{\text{T}}{\bf{y}}_i)^2 =(\color{blue}{r_{1,2}} - \color{red}{x_{1,1}}y_{2,1} - \color{red}{x_{1,2}}y_{2,2})^2 + (\color{blue}{r_{1,3}} - \color{red}{x_{1,1}}y_{3,1} - \color{red}{x_{1,2}}y_{3,2})^2 + \cdots\)

讓損失函數對\(x_{1,1}, x_{1,2}\)分別求偏導數可以得到

\(\frac{\partial{L}}{\partial{\color{red}{x_{1,1}}}}=2(\color{blue}{r_{1,2}} - \color{red}{x_{1,1}}y_{2,1}-\color{red}{x_{1,2}}y_{2,2})(-y_{2,1}) + 2(\color{blue}{r_{1,3}} - \color{red}{x_{1,1}}y_{3,1}-\color{red}{x_{1,2}}y_{3,2})(-y_{3,1}) = 0 \\ \frac{\partial{L}}{\partial{\color{red}{x_{1,2}}}}=2(\color{blue}{r_{1,2}} - \color{red}{x_{1,1}}y_{2,2}-\color{red}{x_{1,2}}y_{2,2})(-y_{2,2}) + 2(\color{blue}{r_{1,3}} - \color{red}{x_{1,1}}y_{3,1}-\color{red}{x_{1,2}}y_{3,2})(-y_{3,2}) = 0\)

寫成矩陣形式可得

利用我們上述的規則，很容易檢驗我們匯出的結論。

總結來說，ALS的整個演演算法過程只有兩步，涉及2個迴圈，如下圖所示：

演演算法使用RMSE（root-mean-square error）評估誤差。

\(rmse = \sqrt{\frac{1}{|K|}\sum\limits_{(u,i) \in K}(r_{u,i}-{\bf{x}}_u^{\text T}{\bf{y}}_i)^2}\)

當RMSE值變化很小時或者到達最大迭代步驟時，滿足收斂條件，停止迭代。

「Talk is cheap. Show me the code.」作為小練習，我們給出上述虛擬碼的Python實現。

import numpy as np
from scipy.linalg import solve as linear_solve
 
# 評分矩陣 5 x 6
R = np.array([[4, 0, 2, 5, 0, 0], [3, 2, 1, 0, 0, 3], [0, 2, 0, 3, 0, 4], [0, 3, 3,5, 4, 0], [5, 0, 3, 4, 0, 0]])
 
m = 5          # 使用者數
n = 6          # 物品數
k = 3          # 隱向量的維度
_lambda = 0.01 # 正則化係數
 
# 隨機初始化使用者矩陣, 物品矩陣
X = np.random.rand(m, k)
Y = np.random.rand(n, k)
 
# 每個使用者打分的物品集合
X_idx_dict = {1: [1, 3, 4], 2: [1, 2, 3, 6], 3: [2, 4, 6], 4: [2, 3, 4, 5], 5: [1, 3, 4]}
 
# 每個物品被打分的使用者集合
Y_idx_dict = {1: [1, 2, 5], 2: [2, 3, 4], 3: [1, 2, 4, 5], 4: [1, 3, 4, 5], 5: [4], 6: [2, 3]}

# 迭代10次
for iter in range(10):
    for u in range(1, m+1):
        Iu = np.array(X_idx_dict[u])
        YIu = Y[Iu-1]
        YIuT = YIu.T
        RuIu = R[u-1, Iu-1]
        xu = linear_solve(YIuT.dot(YIu) + _lambda * np.eye(k), YIuT.dot(RuIu))
        X[u-1] = xu
 
    for i in range(1, n+1):
        Ui = np.array(Y_idx_dict[i])
        XUi = X[Ui-1]
        XUiT = XUi.T
        RiUi = R.T[i-1, Ui-1]
        yi = linear_solve(XUiT.dot(XUi) + _lambda * np.eye(k), XUiT.dot(RiUi))
        Y[i-1] = yi

最終，我們列印使用者矩陣，物品矩陣，預測的評分矩陣如下，可以看到預測的評分矩陣非常逼近原始評分矩陣。

# X
array([[1.30678487, 2.03300876, 3.70447639],
       [4.96150381, 1.03500693, 1.62261161],
       [6.37691007, 2.4290095 , 1.03465981],
       [0.41680155, 3.31805612, 3.24755801],
       [1.26803845, 3.57580564, 2.08450113]])
# Y
array([[ 0.24891282,  1.07434519,  0.40258993],
       [ 0.12832662,  0.17923216,  0.72376732],
       [-0.00149517,  0.77412863,  0.12191856],
       [ 0.12398438,  0.46163336,  1.05188691],
       [ 0.07668894,  0.61050204,  0.59753081],
       [ 0.53437855,  0.20862131,  0.08185176]])
 
# X.dot(Y.T) 預測評分
array([[4.00081359, 3.2132548 , 2.02350084, 4.9972158 , 3.55491072, 1.42566466],
       [3.00018371, 1.99659282, 0.99163666, 2.79974661, 1.98192672, 3.00005934],
       [4.61343295, 2.00253692, 1.99697545, 3.00029418, 2.59019481, 3.99911584],
       [4.97591903, 2.99866546, 2.96391664, 4.99946603, 3.99816006, 1.18076534],
       [4.99647978, 2.31231627, 3.02037696, 4.0005876 , 3.5258348 , 1.59422188]])
 
# 原始評分矩陣
array([[4,          0,           2,         5,          0,          0],
       [3,          2,           1,         0,          0,          3],
       [0,          2,           0,         3,          0,          4],
       [0,          3,           3,         5,          4,          0],
       [5,          0,           3,         4,          0,          0]])

三、Spark ALS應用

Spark的內部實現並不是我們上面所列的演演算法，但是核心原理是完全一樣的，Spark實現的是上述虛擬碼的分散式版本，具體演演算法參考Large-scale Parallel Collaborative Filtering for the Netflix Prize。其次，查閱Spark的官方檔案，我們也注意到，Spark使用的懲罰函數與我們上文的有細微的差別。

\(\lambda \left( \sum\limits_{u}{\color{red}{n_u}\bf{x}}_u^{\text T}{\bf{x}}_u+\sum\limits_{i}{\color{red}{n_i}\bf{y}}_i^{\text T}{\bf{y}}_i\right)\)

其中\(n_u, n_i\)別表示使用者\(u\)打分的物品數量和物品\(i\)被打分的使用者數量。即

\(\begin{cases} n_u = |I_u| \\ n_i = |U_i| \\ \end{cases}\)

本小節通過兩個案例來了解Spark ALS的具體使用，以及在面對網際網路實際工程場景下的應用。

3.1 Demo案例

以第一節給出的資料為例，將三元組(User, Item, Rating)組織為als-demo-data.csv，該demo資料集涉及5個使用者和6個物品。

userId,itemId,rating
1,1,4
1,3,2
1,4,5
2,1,3
2,2,2
2,3,1
2,6,3
3,2,2
3,4,3
3,6,4
4,2,3
4,3,3
4,4,5
4,5,4
5,1,5
5,3,3
5,4,4

使用Spark的ALS類使用非常簡單，只需將三元組(User, Item, Rating)資料輸入模型進行訓練。

import org.apache.spark.sql.SparkSession
import org.apache.spark.ml.recommendation.ALS
  
val spark = SparkSession.builder().appName("als-demo").master("local[*]").getOrCreate()
 
val rating = spark.read
  .options(Map("inferSchema" -> "true", "delimiter" -> ",", "header" -> "true"))
  .csv("./data/als-demo-data.csv")
 
// 展示前5條評分記錄
rating.show(5)
 
val als = new ALS()          
  .setMaxIter(10)             // 迭代次數，用於最小二乘交替迭代的次數
  .setRank(3)                 // 隱向量的維度
  .setRegParam(0.01)          // 懲罰係數
  .setUserCol("userId")       // user_id
  .setItemCol("itemId")       // item_id
  .setRatingCol("rating")     // 評分列
 
val model = als.fit(rating)   // 訓練模型
 
// 列印使用者向量和物品向量
model.userFactors.show(truncate = false)
model.itemFactors.show(truncate = false)
 
// 給所有使用者推薦2個物品
model.recommendForAllUsers(2).show()

上述程式碼在控制檯輸出結果如下：

+------+------+------+
|userId|itemId|rating|
+------+------+------+
|     1|     1|     4|
|     1|     3|     2|
|     1|     4|     5|
|     2|     1|     3|
|     2|     2|     2|
+------+------+------+
only showing top 5 rows
 
+---+------------------------------------+
|id |features                            |
+---+------------------------------------+
|1  |[-0.17339179, 1.3144133, 0.04453602]|
|2  |[-0.3189066, 1.0291641, 0.12700711] |
|3  |[-0.6425665, 1.2283803, 0.26179287] |
|4  |[0.5160747, 0.81320006, -0.57953185]|
|5  |[0.645193, 0.26639006, 0.68648624]  |
+---+------------------------------------+
 
+---+-----------------------------------+
|id |features                           |
+---+-----------------------------------+
|1  |[2.609607, 3.2668495, 3.554771]    |
|2  |[0.85432494, 2.3137972, -1.1198239]|
|3  |[3.280517, 1.9563107, 0.51483333]  |
|4  |[3.7446978, 4.259611, 0.6640027]   |
|5  |[1.6036265, 2.5602736, -1.8897828] |
|6  |[-1.2651576, 2.4723763, 0.51556784]|
+---+-----------------------------------+
 
+------+--------------------------------+
|userId|recommendations                 |
+------+--------------------------------+
|1     |[[4, 4.9791617], [1, 3.9998217]]|   // 對應物品的序號和預測評分
|2     |[[4, 3.273963], [6, 3.0134287]] |
|3     |[[6, 3.9849386], [1, 3.2667015]]|
|4     |[[4, 5.011649], [5, 4.004795]]  |
|5     |[[1, 4.994258], [4, 4.0065994]] |
+------+--------------------------------+

我們使用numpy來驗證Spark的結果，並且用Excel視覺化評分矩陣。

import numpy as np
 
X = np.array([[-0.17339179, 1.3144133, 0.04453602],
              [-0.3189066, 1.0291641, 0.12700711],
              [-0.6425665, 1.2283803, 0.26179287],
              [0.5160747, 0.81320006, -0.57953185],
              [0.645193, 0.26639006, 0.68648624]])
 
Y = np.array([[2.609607, 3.2668495, 3.554771],
              [0.85432494, 2.3137972, -1.1198239],
              [3.280517, 1.9563107, 0.51483333],
              [3.7446978, 4.259611, 0.6640027],
              [1.6036265, 2.5602736, -1.8897828],
              [-1.2651576, 2.4723763, 0.51556784]])
 
R_predict = X.dot(Y.T)
R_predict

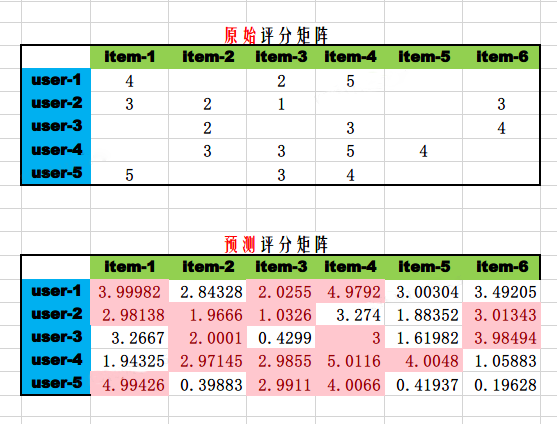
輸出預測的評分矩陣如下：

array([[3.99982136, 2.84328038, 2.02551472, 4.97916153, 3.0030386,  3.49205357],
       [2.98138452, 1.96660155, 1.03257371, 3.27396294, 1.88351875, 3.01342882],
       [3.26670123, 2.0001004 , 0.42992289, 3.00003605, 1.61982132, 3.98493822],
       [1.94325135, 2.97144913, 2.98550149, 5.011649  , 4.00479503, 1.05883274],
       [4.99425778, 0.39883335, 2.99113433, 4.00659955, 0.41937014, 0.19627587]])

從Excel視覺化的評分矩陣可以觀察到預測的評分矩陣非常逼近原始的評分矩陣，以user-3為例，Spark推薦的物品是item-6和item-1, [6, 3.9849386, 1, 3.2667015]，這和Excel展示的預測評分矩陣完全一致。

從Spark函數recommendForAllUsers()給出的結果來看，Spark內部並沒有去除使用者已經購買的物品。

3.2 工程應用

在網際網路場景，使用者數 \(m\)(千萬~億級別) 和物品數 \(n\)(10萬~100萬級別) 規模很大，App的埋點資料一般會儲存在HDFS中，以網際網路的長視訊場景為例，使用者的埋點資訊最終聚合為使用者行為表 t_user_behavior。

行為表包含使用者的imei，物品的content-id，但是沒有直接的使用者評分，實踐中我們的解決方案是利用使用者的其他行為進行加權得出使用者對物品的評分。即

rating = w1 * play_time (播放時長) + w2 * finsh_play_cnt (完成的播放次數) + w3 * praise_cnt (點贊次數) + w4 * share_cnt (分享次數) + 其他適合於你業務邏輯的指標

其中, wi為每個指標對應的權重。

如下的程式碼塊演示了工程實踐中對大規模使用者和商品場景進行推薦的流程。

import org.apache.spark.ml.feature.{IndexToString, StringIndexer}
 
// 從hive載入資料，並利用權重公式計算使用者對物品的評分
val rating_df = spark.sql("select imei, content_id, 權重公式計算評分 as rating from t_user_behavior group by imei, content_id")
 
// 將imei和content_id轉換為序號，Spark ALS入參要求userId, itemId為整數
// 使用org.apache.spark.ml.feature.StringIndexer
val imeiIndexer    = new StringIndexer().setInputCol("imei").setOutputCol("userId").fit(rating_df)
val contentIndexer = new StringIndexer().setInputCol("content_id").setOutputCol("itemId").fit(rating_df)
val ratings = contentIndexer.transform(imeiIndexer.transform(rating_df))
 
// 其他code，類似於上述demo
val model = als.fit(ratings)
 
// 給每個使用者推薦100個物品
val _userRecs = model.recommendForAllUsers(100)
 
// 將userId, itemId轉換為原來的imei和content_id
val imeiConverter    = new IndexToString().setInputCol("userId").setOutputCol("imei").setLabels(imeiIndexer.labels)
val contentConverter = new IndexToString().setInputCol("itemId").setOutputCol("content_id").setLabels(contentIndexer.labels)
val userRecs = imeiConverter.transform(_userRecs)
 
// 離線儲存供線上呼叫
userRecs.foreachPartition {
  // contentConverter 將itemId轉換為content_id
  // 儲存redis邏輯
}

值得注意的是，上述的工程場景還有一種解決方案，即隱式反饋。使用者給商品評分很單一，在實際的場景中，使用者未必會給物品打分，但是大量的使用者行為，同樣能夠間接反映使用者的喜好，比如使用者的購買記錄、搜尋鍵碼，加入購物車，單曲迴圈播放同一首歌。我們將這些間接使用者行為稱之為隱式反饋，以區別於評分對應的顯式反饋。胡一凡等人在論文Collaborative filtering for implicit feedback datasets中針對隱式反饋場景提出了ALS-WR模型 (ALS with Weighted-λ-Regularization)，並且Spark官方也實現了該模型，我們將在以後的文章中介紹該模型。

四、總結

本文從推薦的場景出發，引出了協同過濾這一經典的推薦演演算法，並且由此講解了被Spark唯一實現和維護的矩陣分解演演算法，詳細推導了顯示反饋下矩陣分解的理論原理，並且給出了Python版本的單機實現，能夠讓讀者更好的理解矩陣這一演演算法，最後我們以demo和工程實踐兩個範例講解了Spark ALS的使用，能夠讓沒有接觸過推薦演演算法的同學有個直觀的理解，用理論與實踐的形式明白矩陣分解這一推薦演演算法背後的原理。

參考文獻：

王喆, 深度學習推薦系統
Hu, Yifan, Yehuda Koren, and Chris Volinsky. "Collaborative filtering for implicit feedback datasets." 2008 Eighth IEEE International Conference on Data Mining. IEEE, 2008.
Zhou, Yunhong, et al. "Large-scale parallel collaborative filtering for the Netflix prize." International conference on algorithmic applications in management. Springer, Berlin, Heidelberg, 2008.

推薦系統-協同過濾在Spark中的實現

一、 背景