SVM的另一種解釋

前面已經較為詳細地對SVM進行了推導，前面有提到SVM可以利用梯度下降來進行求解，但並未進行詳細的解釋，本節主要從另一個視角對SVM進行解釋，首先先回顧之前有關SVM的有關內容，然後從機器學習的三步走的角度去對SVM進行一個解釋。

那麼對於傳統的機器學習，每個方法最大區別就是損失函數的選取，因此SVM可以看成是另一種損失函數的方法，這種損失函數就是Hinge Loss。另外SVM另一個特點就是使用了Kenel trick。

0. SVM內容回顧

前面說了SVM（主要是二分類）是希望找一個分離超平面，能夠將資料分開，使得距離分離超平面最近的點的距離越遠越好。

根據優化目標，優化函數變成：

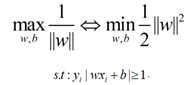
為了使得模型更具有魯棒性和泛化能力，引入一個鬆弛變數ξ：

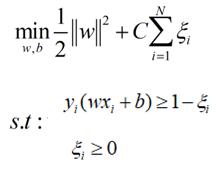
然後就是對這個問題進行求解，主要求解方法就是多目標優化演演算法，引入拉格朗日因子α，問題轉化為求解α，然後最終利用SMO演演算法求解的過程。

因為前面已有這部分內容，這裡就不再贅述了。

下面就是從機器學習通用的方法來解釋SVM演演算法。

1. SVM的另一種解釋

  在前面機器學習中，我們採用三步走：1、找一個function set，2、找一個衡量function好壞的loss function；3、根據loss function找出一個best function。

   也就是我們希望找一個g(x)，使得輸入x使得正類樣本輸出大於0，負類樣本輸出小於0。那麼對於loss function，最理想的情況下，當g(x)=y時，loss=0，當g(x)≠y時，loss=1。但通常δ(g(x)=y)這種loss是不可微的，因此這裡loss function都用l(f(x),y)來表示。通過minimize l(f(x),y)來進行優化求解。具體地loss function也有多種，下面具體看幾個（這裡分類正類為1，負類為-1）：

 

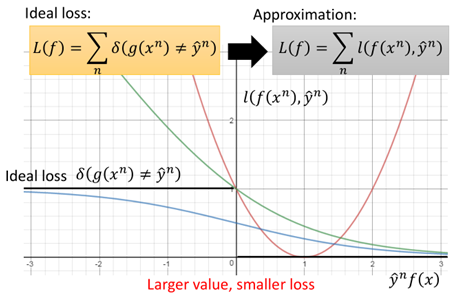
上圖中一共有四種loss function：

①：Ideal loss，就是圖中黑色的那條線，就是理想下的loss function，即當y=1，f(x)>0或y=-1，f(x)<0時loss為0，當二者不同號時loss為1。

②：square loss：也就是圖中紅色的線，其方程形式如下：

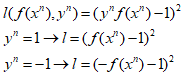
從圖中則可以看出，當y與f(x)不同號時，沒問題，則會有個loss，而當y與f(x)相乘很大時，也會產生一個很大的loss。這也就證明了為什麼在分類時不能使用square loss這樣的損失函數。

③：sigmoid + square loss：也就是圖中藍色的那條線，其方程形式如下：

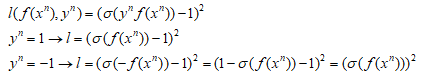
圖中可以看出當y與f(x)不同號時，當這個負數很小時，loss並沒有繼續增加，同樣的當y與f(x)相乘很大時，同樣還是有一個比較小的loss。在LR演演算法中提到過，通常不使用square loss，可能效果不好，這裡可以更容易理解。在LR中往往使用的sigmoid + crossentropy。

④：sigmoid+crossentropy : 就是圖中綠色的那條線，其方程形式及推導如下：

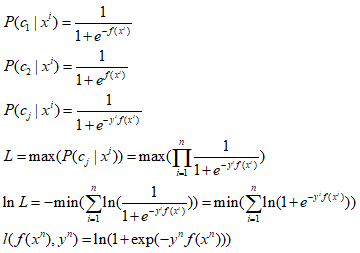
圖中可以看出這個在y與f(x)不同號時，也就是目標值與真實值差距越大，損失也就越大，當y與f(x)相乘很大時，loss是趨於0。因此在分類中更多的是使用crossentropy損失。

  而在SVM中，損失函數使用的則是Hinge Loss損失函數，其函數如圖所示：

Hinge Loss的函數方程為：

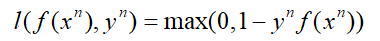
把Hinge Loss與上面的那些損失函數畫在一起進行一個對比：

圖中可以看出，當y與f(x)同號時，且足夠大，則loss=0，而在0~1之間時依然會有一定的損失，而當二者不同號時，loss則持續增大。

相比於cross entropy而言，在二者不同號時，二者基本相似，但是當二者同號，且足夠大時，當大於1時，Hinge loss表現為已經足夠了，不需要再優化了，而對於crossentropy，儘管已經做的很好了，但還是存在一定的loss，還要做的更好。這可能會導致模型的過擬合，因此SVM模型具有更強的泛化能力。

搞定了loss function之後，那麼SVM演演算法的三個步驟如下:

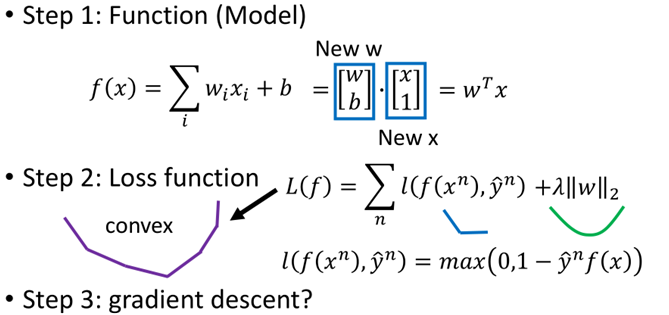
第一步就是一個超平面的集合，這裡將b合併進w中；

第二步就是一個Hinge loss，然後加上一個正則化項，兩個凸函數相加仍然是個凸函數；

第三步就是直接利用梯度下降進行求解，這裡雖然hinge loss存在不可導點，但是並非資料剛好落在不可導的地方，類似於maxpool中的求導。具體求導如下：

至此，SVM另一個角度進行解釋和求解已經完成了，下面我們把這種形式的SVM與傳統的SVM進行一個比較：

這裡令：

那麼損失函數可以寫成：

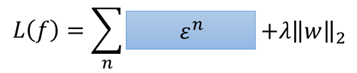
而對於ε這個東西，它與下面這兩個式子：

原本二者不是等價的，因為上面的方框是一個確定的值，而下面的方框則表示的是一個範圍，但是當加上minimize之後，兩個紅色的框上的內容就是等價的。

經過變形yf(x)>1-ε，那麼ε就是鬆弛變數。

2.SVM中的核方法

在說核方法之前，首先是上面問題的求解，在進行梯度下降求解之後，可以得到：

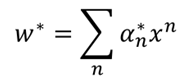
這就是SVM的對偶問題，將求w最後轉化為求α得問題上。而對於上面這個式子，在傳統SVM中，使用的是拉格朗日求極值的方法，從而得到SVM的對偶問題，這裡我們利用梯度下降：

假設初始化w1=0(矩陣)，那麼，最終w則為：

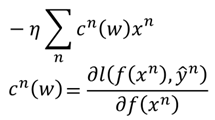
這裡c(w)裡有很多是0的項，因為一部分的求導為0，因此，w*最後就是最開始那個式子，最終問題就變成求解α了，具體求解方法前面SMO演演算法已經說過，這裡就不再說了。

那些不為0的α就是所謂的「支援向量」，這裡也能更好地理解什麼是支援向量。

然後，w就可以寫成下面這樣的形式：

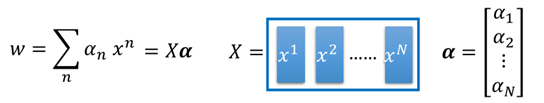
再帶回原方程中f(x)中，則有：

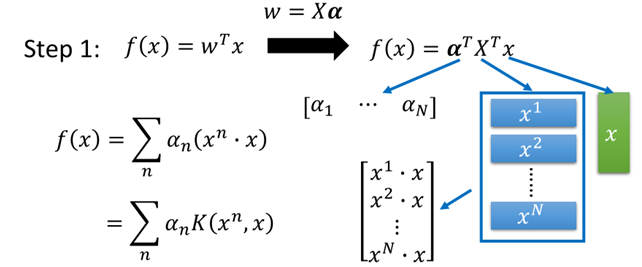
最終f(x)變成了所需要使用核方法的形式：

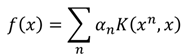
同時，要找一組α={α1，α2，......，αn}，使得損失函數L最小：

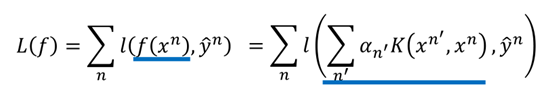
在核技巧中我們並不需要知道x和xn（在高維空間中）是什麼，只需要知道K(xn,x)的值就可以。

直接計算K(x,z)往往比先對映到高維空間再進行內積計算快的多，舉個例子：

有一個x=[x1,x2]，z=[z1,z2]，我們進行轉換，假設先轉換成高維空間中的φ(x)，φ(z)，再相乘：

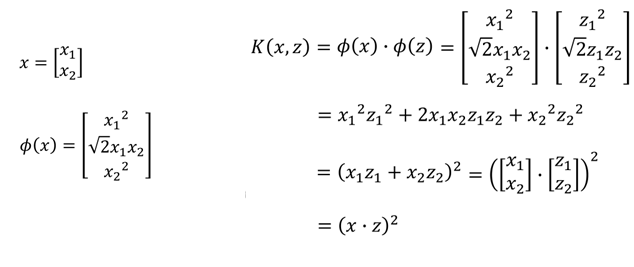
最終可以看到結果和直接進行相乘是一樣的。

假設核函數為tanh函數，那麼就有：

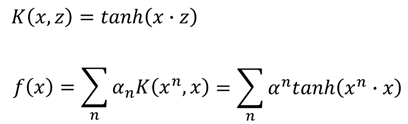
而當核函數是sigmoid函數的時候，那麼此時SVM則可以看成是有一層隱藏層的神經網路：

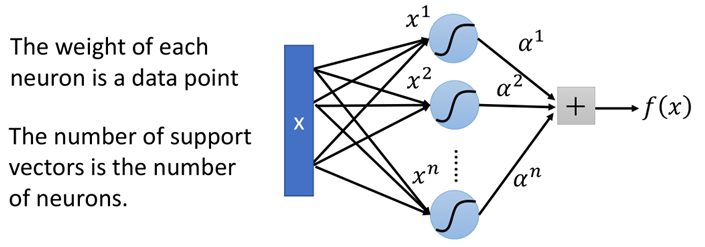
該網路中神經元的個數就是支援向量的個數，而每個權重就是對應的樣本點。

3.小結

上面就是從原始機器學習的角度去看待SVM，從原來求解QP問題的方法轉變為梯度下降的方法，但最終落腳還是要繼續求解α這樣一個問題上。SVM最重要的兩個特點一個是使用了Hinge Loss另一個就是核方法，而核方法在LR中也可以使用，但是由於SVM在進行分類時，只考慮支援向量，因此進行計算時相對較為快速，而LR是所有點參與計算，如果使用核方法則在高維空間中運算量過大，導致效率低，因此LR通常不採用核技巧。此外，相比於LR分類演演算法而言，SVM更具有魯棒性。