技術文章 » 演演算法競賽進階指南 0x52 揹包

演演算法競賽進階指南 0x52 揹包

2022-07-24 12:00:25

揹包問題是線性揹包中的一類重要問題。

0/1揹包

模型：
給定N個物品，每一個物品具有兩種屬性，一個是體積 \(v_i\) ，另一個是容積 \(w_i\) 。
有一個容積為M的揹包，求一種方案，使得選擇的物品的體積不超過揹包體積的情況下，使得獲得的總價值最大。

0/1揹包的時間複雜度是\(O(n*m)\)。

空間複雜度隨著寫法的不同而不同。

方法一：按照定義寫

#include <bits/stdc++.h>
using namespace std;
int n, m;//n表示的是商品的數目，m表示的是揹包的容積。
int f[100][100];
int v[100];//第i個物品的體積
int w[100];//第i個物品的價值
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d", v+i);
    for(int i = 1; i <= n; i++) scanf("%d", w+i);
    memset(f, 0xcf, sizeof(f));
    //求最佳化問題時，把整體全部賦值為無窮大，這樣可以防止不合法的情況對最終的判斷造成干擾
    f[0][0] = 0;
    //只需要賦值這一個就好，隨著DP進行，f[i][0]全部都會是0。
    //雖然f[0][i](i > 0)還是正無窮大，但是對於答案不會造成影響。
    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j <= m; j++) f[i][j] = f[i-1][j];//要注意從0開始進行。
        for(int j = v[i]; j <= m; j++) 
            f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
    }

    return 0;
}

方法二：採用捲動陣列來進行求解。

原理：觀察到更新時所使用到的資訊僅僅與上一行有關係，與其他行並沒有關係。

所以可以採用2*m的捲動陣列。

#include <bits/stdc++.h>
using namespace std;
int n, m;//n表示的是商品的數目，m表示的是揹包的容積。
int f[2][100];
int v[100];//第i個物品的體積
int w[100];//第i個物品的價值
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d", v+i);
    for(int i = 1; i <= n; i++) scanf("%d", w+i);
    memset(f, 0xcf, sizeof(f));
    //求最佳化問題時，把整體全部賦值為無窮大，這樣可以防止不合法的情況對最終的判斷造成干擾
    f[0][0] = 0;
    //只需要賦值這一個就好，隨著DP進行，f[i][0]全部都會是0。
    //雖然f[0][i](i > 0)還是正無窮大，但是對於答案不會造成影響。
    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j <= m; j++) f[i&1][j] = f[(i-1)&1][j];//要注意從0開始進行。
        for(int j = v[i]; j <= m; j++) 
            f[i&1][j] = max(f[i&1][j], f[(i-1)&1][j-v[i]]+w[i]);
    }

    return 0;
}

總結：捲動陣列可以使用位運算&來進行，這樣既可以達到f陣列的維護，還便於計數。

方法三：採用一維陣列進行維護

條件：可以使用捲動陣列進行實現，並且按照一定的掃描順序，更新過的值不會參與到其他值的計算中。

#include <bits/stdc++.h>
using namespace std;
int n, m;//n表示的是商品的數目，m表示的是揹包的容積。
int f[100];
int v[100];//第i個物品的體積
int w[100];//第i個物品的價值
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d", v+i);
    for(int i = 1; i <= n; i++) scanf("%d", w+i);
    memset(f, 0xcf, sizeof(f));
    //求最佳化問題時，把整體全部賦值為無窮大，這樣可以防止不合法的情況對最終的判斷造成干擾
    f[0] = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j-v[i]]+w[i]);
    }

    return 0;
}

AcWing278. 數位組合

給定 N 個正整數 A1,A2,…,A**N，從中選出若干個數，使它們的和為 M，求有多少種選擇方案。

輸入格式

第一行包含兩個整數 N 和 M。

第二行包含 N 個整數，表示 A1,A2,…,A N。

輸出格式

包含一個整數，表示可選方案數。

資料範圍

1≤N≤100,
1≤M≤10000,
1≤A i≤1000,
答案保證在 int 範圍內。

輸入樣例：

4 4
1 1 2 2

輸出樣例：

3

這道題目也可以看做是0/1揹包的變種。
（n個數位選擇一些）

程式碼實現

#include <bits/stdc++.h>
using namespace std;
int f[10020];
int a[102];//儲存每一個數位的大小
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    f[0] = 1;
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    for(int i = 1; i <= n; i++)
    {
        for(int j = m; j >= a[i]; j--)
            f[j] += f[j-a[i]];
    }
    printf("%d", f[m]);
    return 0;
}

細節的考慮

現在從最一開始進行考慮：

對於f[105][10020]，全部初始化為0；

把f[0][0]初始化為1；

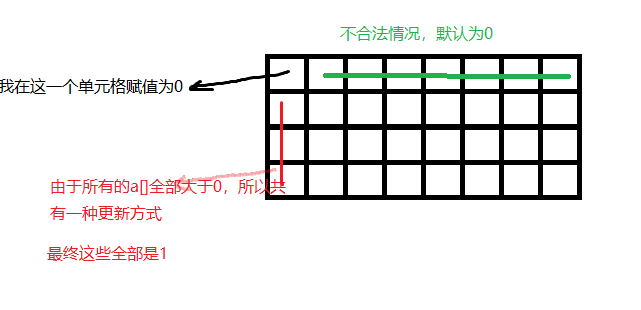
然後優化即可。

完全揹包

模型：
給定N種物品，每一種物品具有兩種屬性，一個是體積 \(v_i\) ，另一個是容積 \(w_i\) 。
有一個容積為M的揹包，求一種方案，使得選擇的物品的體積不超過揹包體積的情況下，使得獲得的總價值最大。
與0/1揹包不同的最大之處在於對於一種物品，可以選擇無數次。

精髓：

對於完全揹包，由於一個物品可以選擇許多次，所以有以下方程

\[f[i][j]=max(f[i][j], f[i-1][j])//表示不選擇第i個物品\\ f[i][j]=max(f[i][j], f[i-1][j-kv_i]+kw_i)(k取值從1開始，讓j\ge kv_i) \]

但是第二步驟顯得過於冗雜，所以不妨優化為

\[f[i][j]=max(f[i][j], f[i][j-v_i]+w_i) \]

上面這一個蘊含玄機：這種情況一定選擇了一種以上，至於到底是多少，並不關心，反正是選擇多次這一個物品，使得總價值最大。

優化：

和0/1揹包一致，使用一維陣列，只不過這一次是要從左向右。

模板

int a[100];//體積
int f[100];
int w[100];//價值
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    for(int i = 1; i <= n; i++) scanf("%d", w+i);
    memset(f, 0xcf, sizeof(f));
    f[0] = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = a[i]; j <= m; j++)
            f[j] = max(f[j], f[j-a[i]]+w[i]);
    }
    return 0;
}

AcWing279. 自然數拆分

給定一個自然數 N，要求把 N 拆分成若干個正整數相加的形式，參與加法運算的數可以重複。

注意:

  • 拆分方案不考慮順序；
  • 至少拆分成 2 個數的和。

求拆分的方案數 mod2147483648 的結果。

輸入格式

一個自然數 N。

輸出格式

輸入一個整數，表示結果。

資料範圍

1≤N≤4000

輸入樣例：

7

輸出樣例：

14

這一種題目看起來簡直不像是揹包問題。。。

但是可以進行歸納：

有體積為1~n的物品以及體積為n的揹包，每一個物品可以放入多次，求使得揹包裝滿的方案數。

#include <bits/stdc++.h>
using namespace std;
#define N 4010
typedef long long ll;
const ll mod = 2147483648;
ll f[N];
int n;
int main()
{
    scanf("%d", &n);
    f[0] = 1;
    for(int i = 1; i <= n; i++)
    {
        for(int j = i; j <= n; j++)
            f[j] = (f[j-i]+f[j])%mod;
    }
    printf("%d", f[n]-1);//因為需要拆分成為兩個數位，所以必須要減去一
    return 0;
}

AcWing280. 陪審團

在一個遙遠的國家，一名嫌疑犯是否有罪需要由陪審團來決定。陪審團是由法官從公民中挑選的。

法官先隨機挑選 N 個人（編號 1,2…,N）作為陪審團的候選人，然後再從這 N 個人中按照下列方法選出 M 人組成陪審團。

首先，參與訴訟的控方和辯方會給所有候選人打分，分值在 0 到 20 之間。第 i 個人的得分分別記為 p[i] 和 d[i]。為了公平起見，法官選出的 M 個人必須滿足：辯方總分 D 和控方總分 P 的差的絕對值 |D−P| 最小。如果選擇方法不唯一，那麼再從中選擇辨控雙方總分之和 D+P 最大的方案。求最終的陪審團獲得的辯方總分 D、控方總分 P，以及陪審團人選的編號。

注意：若陪審團的人選方案不唯一，則任意輸出一組合法方案即可。

輸入格式

輸入包含多組測試資料。每組測試資料第一行包含兩個整數 N 和 M。接下來 N 行，每行包含兩個整數 p[i] 和 d[i]。每組測試資料之間隔一個空行。當輸入資料 N=0，M=0 時，表示結束輸入，該資料無需處理。

輸出格式

對於每組資料，第一行輸出 Jury #C，C 為資料編號，從 1 開始。

第二行輸出 Best jury has value P for prosecution and value D for defence:，P 為控方總分，D 為辯方總分。

第三行輸出按升序排列的陪審人選編號，每個編號前輸出一個空格。

每組資料輸出完後，輸出一個空行。

資料範圍

1≤N≤200,
1≤M≤20
0≤p[i],d[i]≤20

輸入樣例：

4 2
1 2
2 3
4 1
6 2
0 0

輸出樣例：

Jury #1
Best jury has value 6 for prosecution and value 4 for defence:
 2 3

算是比較難的一道題目。

如果使用動態規劃，會發現有四個維度

  1. 在N個人中，已經處理了的人的數目。
  2. 已經選擇的人的數目。
  3. 所有辯方與控方的差。
  4. 辯方以及控方法和。

（要滿足差的絕對值最小的情況下，和最大）

閆氏DP分析法：

狀態表示
f[i][j][k]，i表示考慮過人的數目，j表示選擇的人的數目，k表示差值
把差值相同的視為一個類，集合的屬性就是和最大的方案。
找差最小的時候可以列舉所有差的可能性。

狀態轉移
類似0/1揹包：

  • 如果不選擇第i個人，那麼就會有f[i][j][k] = max(f[i][j][k], f[i-1][j][k]).
  • 如果選擇第i個人，那麼就會有f[i][j][k] = max(f[i][j][k], f[i-1][j-1][ k- ( p[i]-d[i] ) ])

因為最後需要的是方案數，所以需要進行回溯

可以使用結構體存起來，也可以使用到往回推的方式。

在這裡，由於有兩個維度，所以不太好壓縮，
同時由於需要到著往回推算，所以也不能夠壓縮。

感覺這道題目就算不需要求方案數，我也要進行一下回溯。

#include <bits/stdc++.h>
using namespace std;
#define N 205
#define M 25
#define P 805
const int base = 400;//使用base把負的數位對映到正的數位上
int p[N], d[N];
int f[N][M][P];
int ans[M];
int main()
{
    int T = 0;
    int n, m;
    while(scanf("%d%d", &n, &m), n || m)
    {
        for(int i = 1; i <= n; i++) 
        {
            scanf("%d%d", p+i, d+i);
        }
        memset(f, 0xcf, sizeof(f));
        f[0][0][base] = 0;
        //初始值應該是隻有這麼一種合法情況。
        for(int i = 1; i <= n; i++)
            for(int j = 0; j <= m; j++)// ***********從0開始（這樣到最後會有f[i][0][base]全部是0）
            //試想：有f[3][1][2+base](假設p[3]+d[3]==2),那麼如果是選擇了第三個人，那麼退回去f[2][0][base] == 0,合法，
            //而對於其他的f[3][1][xx]，退回去是不合法的情況。
                for(int k = 0; k < P; k++)
                {
                    f[i][j][k] = f[i-1][j][k];
                    int tmp = k-(p[i] - d[i]);
                    //if(tmp < 0 || tmp >= P) continue;//這一句話其實可以省略（因為根據題設條件應該是不會超過範圍）
                    if(j < 1) continue;//這一句話不可以省略。使得j==0的時候不參與第二種情況的更新。
                    f[i][j][k] = max(f[i][j][k], f[i-1][j-1][tmp]+p[i]+d[i]);//注意p[i]+d[i]這裡是加
                }
        int u = 0;
        while(f[n][m][base+u] < 0 && f[n][m][base-u] < 0) u++;//小於0，可以等於0，如果評審團給所有人的打分全部是0
        if(f[n][m][base+u] > f[n][m][base-u]) u = base+u;
        else u = base-u;

        int cnt = 0;
        {
            int i = n, j = m;
            while(j)
            {
                if(f[i][j][u] == f[i-1][j][u])
                {
                    i--;
                }
                else
                {
                    ans[++cnt] = i;
                    u = u-(p[i] - d[i]);
                    i--;
                    j--;
                }
            }
        }
        int sp = 0, sd = 0;
        for(int i = 1; i <= cnt; i++) sp += p[ans[i]], sd += d[ans[i]];
        printf("Jury #%d\n", ++T);
        printf("Best jury has value %d for prosecution and value %d for defence:\n", sp, sd);
        for(int i = cnt; i >= 1; i--) printf(" %d", ans[i]);
        puts("\n");

    }
    return 0;
}

多重揹包

多重揹包是介於0/1揹包以及完全揹包之間的一個問題

模型：
給定N種物品，每一種物品具有三種屬性，一個是體積 \(v_i\) ，一個是容積 \(w_i\) ，還有一個是數量\(num_i\)。
有一個容積為M的揹包，求一種方案，使得選擇的物品的體積不超過揹包體積的情況下，使得獲得的總價值最大。

這裡有三種拆分方法

  1. f[i][j] = max(f[i-1][j], f[i-1][j-v]+w, f[i-1][j-2v]+2w, ....f[i-1][j-sv]+sw)
  2. 直接拆分。
  3. 二進位制拆分。
  4. 使用優先佇列進行優化。

AcWing4. 多重揹包問題 I

有 N 種物品和一個容量是 V 的揹包。第 i 種物品最多有 s**i 件，每件體積是 v**i，價值是 w**i。

求解將哪些物品裝入揹包，可使物品體積總和不超過揹包容量，且價值總和最大。 輸出最大價值。

輸入格式

第一行兩個整數，N，V，用空格隔開，分別表示物品種數和揹包容積。接下來有 N 行，每行三個整數 v**i,w**i,s**i，用空格隔開，分別表示第 i 種物品的體積、價值和數量。

輸出格式

輸出一個整數，表示最大價值。

資料範圍

0<N,V≤100

0<v**i,w**i,s**i≤100

輸入樣例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

輸出樣例：

10

這一道題目資料量很水，所以使用直接拆分（時間複雜度過於高！！！）

#include <bits/stdc++.h>
using namespace std;
#define N 120
int v[N], w[N], s[N];
int f[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    //memset(f, 0xcf, sizeof(f));
    //f[0] = 0;
    //0/1揹包貌似不應該初始化。。。
    for(int i = 1; i <= n; i++) scanf("%d%d%d", v+i, w+i, s+i);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= s[i]; j++)//預設有這麼多。
            for(int k = m; k >= v[i]; k--)
            {
                f[k] = max(f[k], f[k-v[i]]+w[i]);
            }
    printf("%d", f[m]);
    return 0;
}

AcWing5. 多重揹包問題 II

有 N 種物品和一個容量是 V 的揹包。

第 i 種物品最多有 s**i 件，每件體積是 v**i，價值是 w**i。

求解將哪些物品裝入揹包，可使物品體積總和不超過揹包容量，且價值總和最大。 輸出最大價值。

輸入格式

第一行兩個整數，N，V，用空格隔開，分別表示物品種數和揹包容積。

接下來有 N 行，每行三個整數 v**i,w**i,s**i，用空格隔開，分別表示第 i 種物品的體積、價值和數量。

輸出格式

輸出一個整數，表示最大價值。

資料範圍

0<N≤1000
0<V≤2000
0<v i,w i,s i≤2000

提示：

本題考查多重揹包的二進位制優化方法。

輸入樣例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

輸出樣例：

10

這是二進位制拆分的節奏

二進位制拆分太奇妙了！！！！！

如果是直接拆分，相當於是把個數拆分成一堆的1，根據這些1，可以組成任意一種數目。

但是顯然沒有必要。如果使用二進位制拆分，那麼可以根據已有的「虛擬的」物品的選擇與否，組合成任意數目的等價於選擇了\(k(k\in[1, num[i]])\)的這一個物品。

注意：所給定的二進位制數位僅且僅僅可以表示出0~num[i]的數位

#include <bits/stdc++.h>
using namespace std;
#define N 2020
int s[N], w[N], v[N];
struct QWER{
    int w, v;
};
vector<QWER>vec;
int f[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%d%d%d", w+i, v+i, s+i);
    for(int i = 1; i <= n; i++)
    {
        int t = s[i];
        for(int k = 1; k <= t; k *= 2)
        {
            t -= k;
            vec.push_back({w[i]*k, v[i]*k});
        }
        if(t > 0) vec.push_back({w[i]*t, v[i]*t});
    }
    for(int i = 0; i < vec.size(); i++)
    {
        int val = vec[i].v;
        int wei = vec[i].w;
        for(int j = m; j >= wei; j--)
        {
            f[j] = max(f[j], f[j-wei]+val);
        }
        //printf("%d %d \n", val, wei);
    }
    
    printf("%d", f[m]);
    return 0;
}

AcWing281. 硬幣

給定 N 種硬幣，其中第 i 種硬幣的面值為 A i，共有 C i 個。

從中選出若干個硬幣，把面值相加，若結果為 S，則稱「面值 S 能被拼成」。求 1∼M 之間能被拼成的面值有多少個。

輸入格式

輸入包含多組測試用例。每組測試用例第一行包含兩個整數 N 和 M。

第二行包含 2N 個整數，分別表示 A1,A2,…,A**N 和 C1,C2,…,C**N。

當輸入用例 N=0，M=0 時，表示輸入終止，且該用例無需處理。

輸出格式

每組用例輸出一個結果，每個結果佔一行。

資料範圍

\(1≤N≤100\),
\(1≤M≤10^5\),
\(1≤A_i≤10^5\),
\(1≤C_i≤1000\)

輸入用例：

3 10
1 2 4 2 1 1
2 5
1 4 2 1
0 0

輸出用例：

8
4

雖然是POJ的"男人八題",但是還是可以做的。

對於這裡，最樸素的做法int f[][]。
其中，f[i][j]表示：在考慮了前i個物品，體積恰好是j的所選物品的集合。
屬性是：這個集合內是否有元素（是一個bool值）

對於第 i 個物品，有狀態轉移方程
f[i][j] = f[i-1][j] || f[i-1][j-v] || f[i-1][j-2v]...。

這一個是最樸素的轉移方程，由於這一道題會卡常，所以要通過最樸素的方式尋找常數更加少的方案。

在尋找是否有一個1的時候，可以採用陣列g保留與該位置最近的1距離該位置是多遠。
如果距離大於s，那麼不可以
如果距離小於等於s，那麼可以

AcWing9. 分組揹包問題

有 N 組物品和一個容量是 V 的揹包。

每組物品有若干個，同一組內的物品最多隻能選一個。 每件物品的體積是 vij，價值是 wij，其中 i 是組號，j 是組內編號。求解將哪些物品裝入揹包，可使物品總體積不超過揹包容量，且總價值最大。輸出最大價值。

輸入格式

第一行有兩個整數 N，V，用空格隔開，分別表示物品組數和揹包容量。接下來有 N 組資料：

  • 每組資料第一行有一個整數 S i，表示第 i 個物品組的物品數量；
  • 每組資料接下來有 S i 行，每行有兩個整數 v i j,w i j，用空格隔開，分別表示第 i 個物品組的第 j個物品的體積和價值；

輸出格式

輸出一個整數，表示最大價值。

資料範圍

0<N,V≤100
0<S i≤100
0<v i j,w** i j≤100

輸入樣例

3 5
2
1 2
2 4
1
3 4
1
4 5

輸出樣例：

8

其實也沒有什麼好的優化方法，直接\(N^3\)暴力進行。

#include <bits/stdc++.h>
using namespace std;
#define N 105
int v[N], w[N];
int f[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        int c;
        scanf("%d", &c);
        for(int j = 1; j <= c; j++) scanf("%d%d", v+j, w+j);
        for(int j = m; j >= 0; j--)
        {
            for(int k = 1; k <= c; k++)
                if(v[k] <= j)
                    f[j] = max(f[j], f[j-v[k]]+w[k]);
        }
    }
    printf("%d", f[m]);
    return 0;
}