技術文章 » 【學習筆記】帶你從0開始學習 01Trie

【學習筆記】帶你從0開始學習 01Trie

2022-07-21 21:00:38

01Trie

Section 1：普通 Trie

Section 1.1 什麼是 Trie

Trie 樹，即字典樹，是一種樹形結構。典型應用是用於統計和排序大量的字串字首來減少查詢時間，最大限度地減少無謂的字串比較。

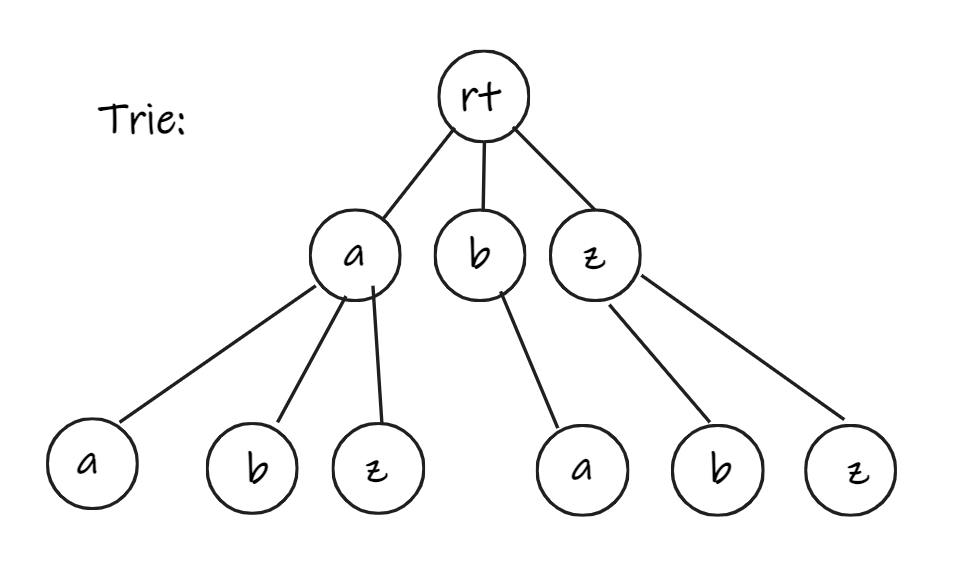
Section 1.2 如何實現

具體地說，對於每個結點，我們要儲存幾個資訊：

  • ch[26] ，儲存此字元的下一個字元（\(a\sim z\)）的儲存地址（沒有為 \(0\)）。
  • cnt ，儲存此節點被經過了多少次。

對於整個 Trie 樹，我們還要額外儲存

  • Tcnt，為節點數。
  • Endp[]，表示的是這個字串是否以這個下標結尾（如果只是看是否是字首，則不需要此陣列）。

幾個操作

  1. insert：往 Trie 樹裡插入一個字串。

具體實現：把字串裡的字元掃描一遍，設當前字元為 \(s\)，如果 ch[s-'a'] 不等於 \(0\)，跳轉到 ch[s-'a'] 的儲存下標。否則把 ch[s-'a'] 設為樹的節點數加一，然後跳轉。跳轉時把當前節點的 \(cnt\) 加一。

跳到最後把當前節點 \(Endp\) 設為一。

  1. find：查詢 Trie 裡是否有這個字串。

具體實現：根據每個字元一個一個跳。

如果跳的時候 \(cnt=0\)，說明沒有。
如果跳到最後，有，但是 \(Endp_{nowNode}=0\) 即並不是以這個字元結尾的，說明沒有。
否則有這個字串，返回 true。

Section 1.3 程式碼實現

(只給出基礎的插入和查詢出現次數)

點選檢視程式碼 
#include <bits/stdc++.h>
using namespace std;

const int N=3000005;

struct Trie{
	int T[N][63],Tsiz,Endp[N];
	void init(){
		for(int i=0;i<=Tsiz;i++) for(int j=0;j<=62;j++) T[i][j]=0;
		for(int i=1;i<=Tsiz;i++) Endp[i]=0;
		Tsiz=0;
	}
	int gethash(char ch){
		if(islower(ch)) return ch-'a';
		if(isupper(ch)) return ch-'A'+26;
		if(isdigit(ch)) return ch-'0'+26+26;
	}
	void insert(string s){
		int rt=0,len=s.length();
		for(int i=0;i<len;i++){
			int x=gethash(s[i]);
			if(!T[rt][x]) T[rt][x]=++Tsiz;
			rt=T[rt][x];
		}
		Endp[rt]++;
	}
	int find(string s){
		int rt=0,len=s.length();
		for(int i=0;i<len;i++){
			int x=gethash(s[i]);
			if(!T[rt][x]) return 0;
			rt=T[rt][x];
		}
		return Endp[rt];
	}
}trie;

int T,n,q;

int main(){
	trie.init();
	cin>>n>>q;
	string s;
	for(int i=1;i<=n;i++){
		cin>>s;
		trie.insert(s);
	}
	for(int i=1;i<=q;i++){
		cin>>s;
		cout<<trie.find(s)<<'\n';
	}
}

Section 1.4 模板

【洛谷模板題 Link】

（使用以上程式碼無法通過此題，請寫 \(cnt\) 維護字首）

Section 2：01Trie

Section 2.1 什麼是 01Trie?

和普通 Trie 相似，但是每個節點只有兩個值：\(0/1\)。

從根節點至下的一條路徑儲存著一個正整數從高到低的二進位制位。

如下圖：

中序遍歷結果為（忽略根節點）： \(00\ 01\ 10\ 11\)

我們會發現幾點有趣的性質：

  • 01Trie 是一棵二元樹，每個節點的左兒子為 \(0\)，右兒子為 \(1\)。
  • 從根節點往下，所有左兒子開始的路徑值都小於右兒子開始的路徑值。

運用這兩點性質，我們就可以用 01Trie 造一棵平衡樹。

Section 2.2 平衡樹

對於每個節點，我們維護兩個資訊：

  • siz，維護以當前節點為根節點的子樹大小。
  • cnt，維護數位到當前節點為二進位制的最後一位的數位個數。

此外，和普通 Trie 一樣，我們還要維護樹的大小 \(p\)。

幾個操作

  1. insert：平衡樹的插入操作。首先，給每個經過的結點的 \(siz\) 加一，表示子樹節點的個數多了一個。如果當前數位的當前二進位制位為 \(0\)，就把他放在左兒子，否則放在右兒子。插入到最後一位時給當前節點的 \(cnt\) 加 \(1\)。

  2. delete：平衡樹的刪除操作，與 insert 幾乎一樣，只是把最後一位 \(cnt-1\) 就行了。

  3. get_rank：查詢當前數的排名。從根節點開始往下，如果當前數的當前二進位制位為 \(1\)，就把排名加上它的左子樹的值（性質二）。

  4. get_kth：查詢排名為 \(k\) 的數。從根節點往下，設它的左子樹 \(siz\) 為 \(tmp\)，則如果 \(k \le tmp\)，則說明排名為 \(k\) 的節點在它的左子樹上。否則向右子樹查詢，並把答案的當前二進位制位設為 \(1\)。

  5. pre：求當前數的前驅。返回 get_kth(get_rank(x)) 即可。

  6. nxt：求當前數的後繼。返回 get_kth(get_rank(x+1)+1) 即可。

Section 2.3 程式碼實現

點選檢視程式碼 
#include <bits/stdc++.h>
using namespace std;

const int MAXLOG=24;
const int N=1e7;

class _01trie{
private:
	struct node{
		int ch[2];
		int siz,cnt;
	}T[1<<MAXLOG];
	int p;
public:
	void update(int x,int offset){
		int now=0;
		for(int i=MAXLOG-1;i>=0;i--){
			bool now_bit=(x&(1<<i));
			if(T[now].ch[now_bit]==0) 
				T[now].ch[now_bit]=++p;
			now=T[now].ch[now_bit];
			T[now].siz+=offset;
		}
		T[now].cnt+=offset;
	}
	int get_rank(int x){
		int now=0,ans=0;
		for(int i=MAXLOG-1;i>=0;i--){
			bool now_bit=(x&(1<<i));
			if(now_bit==1)
				ans+=T[T[now].ch[0]].siz;
			now=T[now].ch[now_bit];
			if(now==0)
				break;
		}
		return ans;
	}
	int get_kth(int k){
		int now=0,ans=0;
		for(int i=MAXLOG-1;i>=0;i--){
			int tmp=T[T[now].ch[0]].siz;
			if(k<=tmp)
				now=T[now].ch[0];
			else{
				k-=tmp;
				now=T[now].ch[1];
				ans|=(1<<i);
			}
			if(now==0)
				break;
		}
		return ans;
	}
	int pre(int x){
		return get_kth(get_rank(x));
	}
	int nxt(int x){
		return get_kth(get_rank(x+1)+1);
	}
}Trie;

int n;
int opt,x;

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&opt,&x);
		if(opt==1) Trie.update(x+N,1);
		if(opt==2) Trie.update(x+N,-1);
		if(opt==3) printf("%d\n",Trie.get_rank(x+N)+1);
		if(opt==4) printf("%d\n",Trie.get_kth(x)-N);
		if(opt==5) printf("%d\n",Trie.pre(x+N)-N);
		if(opt==6) printf("%d\n",Trie.nxt(x+N)-N);
	}
}

Section 2.4 模板

【洛谷模板題 Link】

Section 3：01Trie 例題

洛谷 P4551 最長互斥或路徑

Description
給定一棵樹和樹上的邊權，求兩點之間路徑互斥或值的最大值。

Solution

先給定一個前置知識：\(x \oplus x=0\)。

所以樹上兩點路徑的互斥或值等於根節點分別向兩點的路徑互斥或值的互斥或（\(root \to \operatorname{LCA} (x,y)\) 那一段的互斥或值被抵消了）。

所以我們可以一遍 dfs 處理出根節點到所有節點的邊權互斥或值，隨後把它們扔進 01Trie 中。為了讓互斥或值最大，我們可以列舉節點，在 Trie 上貪心：從高到低位，儘量選和當前數二進位制位不一樣的，隨後再與原節點互斥或值互斥或一下，取 \(\max\) 即可。

Code

點選檢視程式碼 
#include <bits/stdc++.h>
using namespace std;

const int MAXLOG=31;
const int N=3e5+5;

class _01trie{
private:
	struct node{
		int ch[2];
		int siz,cnt;
	}T[N<<5];
	int p;
public:
	void update(int x){
		int now=0;
		for(int i=MAXLOG-1;i>=0;i--){
			bool b=(x&(1<<i));
			if(T[now].ch[b]==0) 
				T[now].ch[b]=++p;
			now=T[now].ch[b];
		}
	}
	int query(int x){
		int now=0,ans=0;
		for(int i=MAXLOG-1;i>=0;i--){
			bool b=(x&(1<<i));
			if(T[now].ch[b^1]){
				ans=ans<<1|(b^1);
				now=T[now].ch[b^1];
			}
			else{
				ans=ans<<1|b;
				now=T[now].ch[b];
			}
		}
		return ans;
	}
}Trie;

int n;

struct Graph{
	int to,w,next;
}G[N<<1];
int head[N],cnt;
void addEdge(int u,int v,int w){G[++cnt]=(Graph){v,w,head[u]}; head[u]=cnt;}

int val[N];

void dfs(int x,int fa){
	for(int i=head[x];i;i=G[i].next){
		int t=G[i].to;
		if(t==fa) continue;
		val[t]=val[x]^G[i].w;
		dfs(t,x);
	}
}

int main(){
	cin>>n;
	for(int i=1;i<n;i++){
		int u,v,w;
		cin>>u>>v>>w;
		addEdge(u,v,w);
		addEdge(v,u,w);
	}
	dfs(1,0);
	for(int i=1;i<=n;i++) Trie.update(val[i]);
	int maxx=0;
	for(int i=1;i<=n;i++) maxx=max(maxx,Trie.query(val[i])^val[i]);
	cout<<maxx;
}