可數集與不可數集

本文為基於「《機器學習的數學》- 第1章一元函數微積分 - 1.1 極限與連續 - 1.1.1 可數集與不可數集」的學習筆記

知識脈絡梳理

本節的重點在於理解可數與不可數的概念，它們將用於定積分中函數的可積性，以及概率論中的離散型與連續型隨機變數等重要概念中。
可數集是在「集合等勢」概念的基礎上進行定義的，因此要理解可數與不可數首先要理解什麼是集合等勢。
本節的討論範圍是「有限集+無限集」，而初等數學的主要討論物件是有限集。
當我們面對「無窮」問題時，必須建立以下幾個基本觀點：1)有限到無限是從量變到質變；2)有限集的性質不能推廣到無限，反之亦然；3)要依靠理性的論證，而不是直觀和常識來認識無限。
因此首先要放棄以前初等數學中（有限）集合的知識，重現建立「有限集+無限集」下集合的嚴格定義。

一、初等數學中對有限集/無限集及其基數的理解

在初等數學中：

對有限集和無限集的理解僅僅停留在「直觀理解」層面：元素個數有限的集合是有限集；元素個數無限的集合是無限集。
用集合中元素的個數（基數）作為集合大小的度量方式，比如集合$A=\{a,b,c,d,e,f,g,h\}$中有8個元素，因此集合$A$的基數就是8，記為$|A|=8$；
可以將集合的基數看作數值直接進行比較，比如集合$|A|=80$，$|B|=100$，因為 $80 < 100$，所以 $|A| < |B|$；
定義了集合間的基本關係（子集、真子集、相等）以及集合的基本運算（交集、並集、補集）。
經常利用集合間關係和維恩圖的直觀理解進行集合基數的相關運算，比如：
- $|A \cup B| = |A| + |B| - |A \cap B| $
- 如果$A \subset B$，則$|A|<|B|$
- 如果$A \cap B = \emptyset$，則$|A|+|B|=|A \cup B| $
- ...

當擴充套件到無限集時，初等數學中的有些概念和規則不再適用，比如：

對無限集討論元素個數是沒有意義的，因為所有無限集元素的個數都是$+\infty$
某些在有限集下成立的性質在無限集中不再成立，比如「如果$A \subset B$，則$|A|<|B|$」這條性質就不在成立，舉例說明如下：
【例1】對下面幾個集合的基數進行比較：
1. 正整數集 $\mathbb{N^+}$
2. 正奇數集 $A_1$
3. 正偶數集 $A_2$
對於【例1】中提到的這三個集合，有下面幾組集合關係：

\[ \mathbb{N^+} = A_1 \cup A_2 \\ A_1 \subset \mathbb{N^+} \\ A_2 \subset \mathbb{N^+} \\ A_1 \cap A_2 = \emptyset \]
這是否意味著 $|A_1| <|\mathbb{N^+}|$ 、 $|A_2| <|\mathbb{N^+}|$ 或 $|A_1|+|A_2|=|\mathbb{N^+}|$ 呢？答案是否定的（實際上這三個集合是等勢的）。

因此，我們需要對有限集和無限集重新進行定義，並重新審視以前不假思索就直接使用的很多性質和規則。

二、基數的本質

在初等數學中：
...
2. 用集合中元素的個數（基數）作為集合大小的度量方式，比如集合$A=\{a,b,c,d,e,f,g,h\}$中有8個元素，因此集合$A$的基數就是8，記為$|A|=8$$
...

我們來深入思考$|A|=8$這一簡單結論背後的思想：

判斷一個有限集合中元素的「多少」，其實是採用「數數」的方法。比如在集合$A$中：a是第一個元素、b是第二個元素、...、h是第8個元素；一個一個去數集合中的元素，等到把所有的元素都數完了（因為是有限集所有才有可能數完），得出該集合中一共有8個元素的結論。
「數數」的過程其實就是與有限集合$N_n=\{1,2,...,n\}$建立「一一對應」的對映關係的過程。比如計算集合$A$中元素個數的過程實際上就是建立如下圖所示的對映關係的過程：

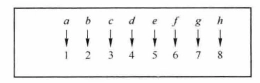
注：在集合基數及其比較.ppt中對「基數的本質」有一些很有意思的討論，可以瞭解一下。

三、有限集和無限集的定義

一個集合「能夠與有限集合$N_n=\{1,2,...,n\}$建立一一對應的對映關係」實際上就是說：如果一個一個數，該集合中的元素是可以數完的。在這樣的考慮下可以重新對有限集和無限集進行定義：

【定義1】一個集合$S$與集合$N_n=\{1,2,...,n\}$（定義$N_0 = \emptyset$）之間如果存在一一對應函數 $f: S \rightarrow N_n$，則稱$S$是有限集，否則稱$S$是無限集。

【定義2】有限集$S$的元素的個數稱為S的基數，記為$|S|$。

例如，下列集合均為有限集：

注意：

無限集是指「不能與集合$N_n$建立一一對應關係的集合」，而不是「能與$N_n$建立一一對應關係，但n為無窮大的集合（此時$N_n$其實就是正整數集 $\mathbb{N^+} $ ）（這其實是可數集的定義）」。
「能與$N_n$建立一一對應關係」意味著可以一個一個數，而有的無限集比如實數集是根本就不能計數的。

四、集合等勢

假設集合$A=\{a,b,c,d,e,f,g,h\}, B=\{1月, 2月, 3月, ... , 8月\}$，很容易可以得出「集合$A$和集合$B$的基數相等」的結論，下面思考這一結論是如何得出的？

集合$A=\{a,b,c,d,e,f,g,h\}$可以與有限集合$N_8 = \{1, 2, 3, ..., 8\}$建立一一對映關係
=> 集合$A$中有8個元素，$|A|=8$
集合$B=\{1月, 2月, 3月, ... , 8月\}$可以與有限集合$N_8 = \{1, 2, 3, ..., 8\}$建立一一對映關係
=> 集合$B$中有8個元素，$|B|=8$
因為$|A|=|B|=8$，所以集合$A$和集合$B$的基數相等

從表面上看，得出「集合$A$和集合$B$的基數相等」這一結論的原因似乎是$|A|=|B|=8$，本質上卻是「集合$A$和集合$B$都能與有限集合$N_8 = \{1, 2, 3, ..., 8\}$建立一一對映關係」，進一步說實際上是「集合$A$和集合$B$能夠建立一一對映關係」。

在這樣的考慮下給出兩個集合等勢的定義：

【定義2】對於集合$A$和集合$B$，如果集合$A$中的任意元素$a$，在集合$B$中都有唯一的元素$b$通過某種對映關係與之對應，即存在如下的從$A$到$B$的雙射函數（Bijection，一對一對映函數）

\[b=f(a), a \in A, b \in B, f: A \rightarrow B \]
則稱集合$A$與集合$B$等勢，記為$A \sim B$

集合的勢是一個用來度量集合所含元素多少的量。集合的勢越大，所含的元素越多。
兩個集合等勢的定義中並沒有對集合的型別進行限制，也就是說上面的定義對有限集和無限集都適用
- 有限集可以直擊計算出元素個數（基數），一般不用「勢」來度量元素的個數

在【例1】中曾經提到過「正整數集 $\mathbb{N^+}$、正奇數集 $A_1$和正偶數集 $A_2$兩兩之間等勢」，下面對這一結論進行說明：

正整數集 $\mathbb{N^+}$與正偶數集 $A_2$等勢：

對於集合$\mathbb{N^+}$中的每一個元素$i$，都有$A_2$中的元素$2i$與之對應；反過來$A_2$中的元素$i$也都有 $\mathbb{N^+}$中的元素$\frac{i}{2}$與之對應。
即存在從集合$\mathbb{N^+}$到集合$A_2$的雙射關係：$i \rightarrow 2i, i \in \mathbb{N^+}, 2i \in A_2$。
因此，正整數集 $\mathbb{N^+}$與正偶數集 $A_2$等勢

同理：

因為存在從集合$\mathbb{N^+}$到集合$A_1$的雙射關係：$i \rightarrow 2i-1, i \in \mathbb{N^+}, 2i-1 \in A_1$，所以正整數集 $\mathbb{N^+}$與正奇數集 $A_1$等勢；
因為存在從集合$A_1$到集合$A_2$的雙射關係：$i \rightarrow i+1, i \in A_1, i+1 \in A_2$，所以正奇數集 $A_1$與正偶數集 $A_2$等勢。

再舉一個連續集合的例子：實數集 $\mathbb{R}$與區間 $(0, 1)$等勢

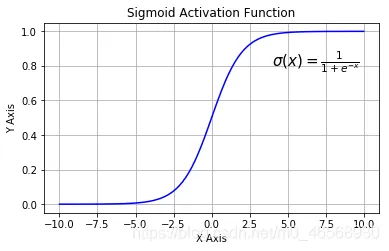
因為存在從實數集 $\mathbb{R}$到區間 $(0, 1)$的雙射函數：$f(x) = \frac{1}{1+e^{-x}}, x \in \mathbb{R}$，所以實數集 $\mathbb{R}$與區間 $(0, 1)$等勢
這一函數也稱為logistic函數或sigmoid函數，其函數影象如下圖所示：

五、可數集與不可數集

【定義3】如果集合$S$能與正整數集 $\mathbb{N^+}$建立一一對應的對映關係，即存在從正整數集 $\mathbb{N^+}$到集合$S$的雙射關係：$f: \mathbb{N^+} \rightarrow S$，則稱集合$S$是可數的。換句話說，與正整數集 $\mathbb{N^+}$等勢的集合稱為可數集。

5.2 對「可數」的理解

因為一開始對「可數」這一概念實在是不能理解，所以查閱了很多資料，先將其中一部分我認為有價值的列出來，這些資料分別從不同角度對「可數」的概念進行了解釋：

百度百科：

可數集（Countable set），是指每個元素都能與自然數集N的每個元素之間能建立一一對應的集合。如果將可數集的每個元素標上與它對應的那個自然數記號，那麼可數集的元素就可以按自然數的順序排成一個無窮序列 a1，a2，a3，…an，…。

以下是判斷一個集合是可數集合的一些結論。

按照可數集合的定義，若A為有限集，則A一定是可數集合，否則若A與自然數集之間存在一個一一對應的對映，則A為可數集合。
若A與某可數集合之間存在一一對應的對映，則A為可數集合。
若A中所有元素可按某種規律進行排序，則A是可數集合。
若A是n(>1)個可數集合的並集，則A是可數集合。
若A是某個已知是可數集合的子集，則A是可數集合。
若A是n(>1)個可數集合的笛卡兒乘積，則A是可數集合。

維基百科：

在數學上，可數集，或稱可列集，是與自然數集的某個子集具有相同基數（等勢）的集合。在這個意義下，可數集由有限可數集和無限可數集組成。不是可數集的無窮集稱為不可數集。這個術語是康托爾創造的。可數集的元素，正如其名，是「可以計數」的：儘管計數有可能永遠無法終止，集合中每一個特定的元素都將對應一個自然數。

「可數集」這個術語有時僅僅指代無限可數集，即僅代表能和自然數集本身一一對應的集合。兩個定義的差別在於有限集合在前者中算作可數集，而在後者中不算作可數集。為了避免歧義，前一種意義上的可數有時稱為至多可數，後一種可數集則稱為無限可數集。

可列怎麼理解？ - 趙莉莉的回答 - 知乎

...它無非是將我們數數（shǔ shù）的行為進行了數學定義。因為日常，當我們數數的時候，就是沿著自然數的元素一個個數一些物件的個數的...

可列集是不是能全列出來就算可列集？還有定義中的某種規律指的是什麼？ - Dr.eam的回答 - 知乎

問：可列集是不是能全列出來就算可列集？
答：不是說能全列出來，理論上的意思是你對於一個可列集中的元素你總能在排序中確定一個他的位置，或者說這個集合與正整數集存在一一對應關係才叫可列，全列出來是不可能的，因為畢竟是無限集，不過可以說能夠一直列下去。

無限集中，所有的可數集都是等勢的，其中可數等價於可列，即所有元素可以排成一個無窮數列{a_i}，其中對於集合中的每一個元素，總存在唯一一個自然數下標n，使得a_n就是這個元素。

總結： 其實對「可數」最好的解釋就是「可以一個一個地數」或者「可以計數」。

本文在「2.1基數的本質」中已經對「計數」這一行為進行了討論，下面通過對什麼是「不可計數」進行說明，以便更好地理解：

【例2】實數集$\mathbb{R}$或長度不為0的實數區間是不可數的。

這些集合中的元素是連續的，它們在數軸上是相當稠密的。

對於長度不為0的實數區間$(a_1,a_2)$，在該區間內任意兩個不相等的實數（不論它們之間的距離有多近）之間都有無數個實數，它們之間的這些實數同樣也屬於$(a_1,a_2)$實數區間。

考慮一個實數區間 $ [1, 10 ]$，試圖對它所包含的實數進行計數。一開始先間隔1取數進行計數，數了10個數：1到10；這時發現剛剛取到的10個數中相鄰兩個數之間仍有無數個數，於是先試著數一數1和2之間的數，這次間隔0.1取數，取到了1.0、1.1、...、1.9、2.0這11個數；然後發現1.1和1.2之間還有無數個數，繼續用更小的間隔0.01取數：1.00、1.01、...、1.09、1.10；...這樣的過程似乎可以無止盡地進行下去，即使數到了1.0000000000000000001和1.0000000000000000002，它們之間還是有無窮多個數。最後發現根本沒有辦法對它進行計數。

「無法計數」並不是說「數不完」，「數不完」的含義其實是「可以數」但是「計數的過程會無止境地進行下去」，「數不完」說的是無限可數集的情況，比如對於正偶數集，我可以按照2、4、6、8、10、...的規律一直往下數但是永遠也數不完。

5.4 連續/離散與可數/不可數的關係

離散與可數是等價的

5.5 一些可數集的例子

自然數集$\mathbb{N}$
整數集$\mathbb{Z}$
對於所有的整數$... ,-4, -3, -2, -1, 0, 1, 2, 3, 4, ...$可以按照下面的順序一直數下去：$0, 1,-1,2,-2,3,-3,4,-4,...$
有理數集$\mathbb{Q}$

【機器學習的數學01】可數集與不可數集