聯邦學習: 聯邦場景下的時空資料探勘

不論你望得多遠，仍然有無限的空間在外邊，不論你數多久，仍然有無限的時間數不清。——惠特曼《自己之歌》

1. 導引

時空資料探勘做為智慧城市的重要組成部分，和我們的日常生活息息相關。如我們開啟地圖軟體，會根據交通流量的預測為我們推薦路線；通過網約車軟體下單，會為我們就近做訂單匹配等等。

然而，時空資料探勘在實際使用的過程中會面臨一個難點，那就是跨平臺共同作業。比如在疫情期間，我們需要對確診病例的行程軌跡做追溯。而我們知道，一個人在行程中可能會使用多個軟體，比如滴滴出行、共用單車乃至健身軟體等。而如何讓資訊在不同平臺間共用便成為難點。

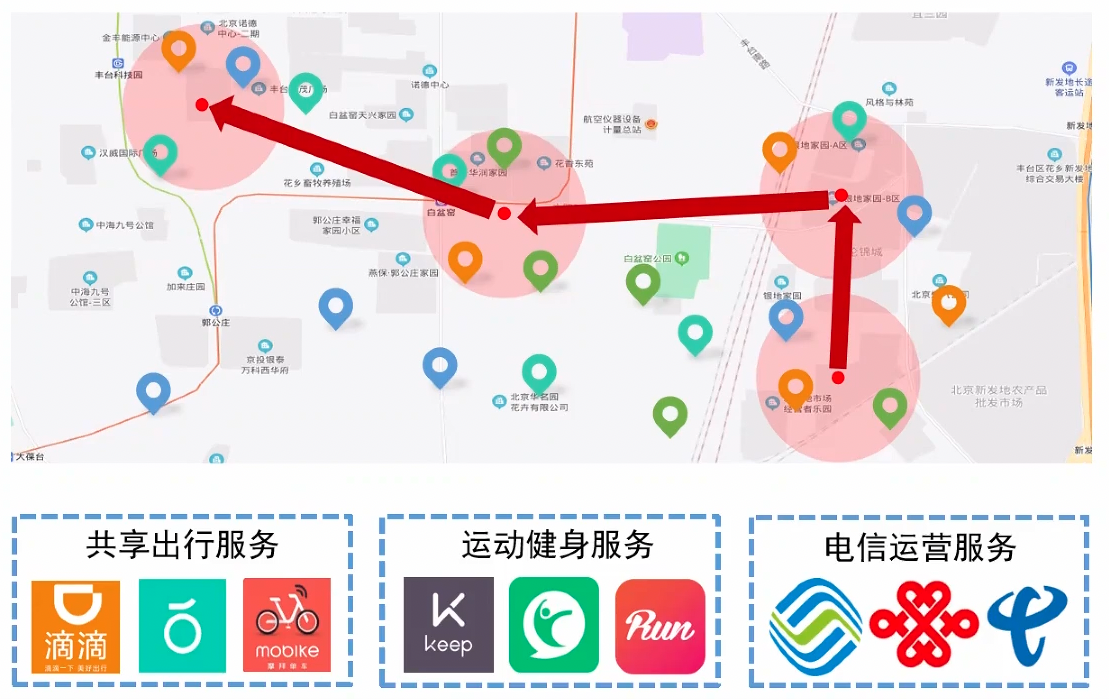
此外，在打車場景中也會面臨此問題。一個使用者在A於高峰期在平臺A叫了一輛車，但是周圍沒有司機，訂單因此取消了。然而，另一個平臺B在周圍有空閒的司機。而由於資料隔絕，該訂單並不能夠被B接收，這樣就白白造成了資源的浪費，不僅降低了平臺的收入也降低了使用者的體驗。

時空聯邦計算是對該問題的一個有效解決方式。「資料不動計算動」的思想能夠有效打破資料孤島（data silo），實現跨平臺的資訊共用。

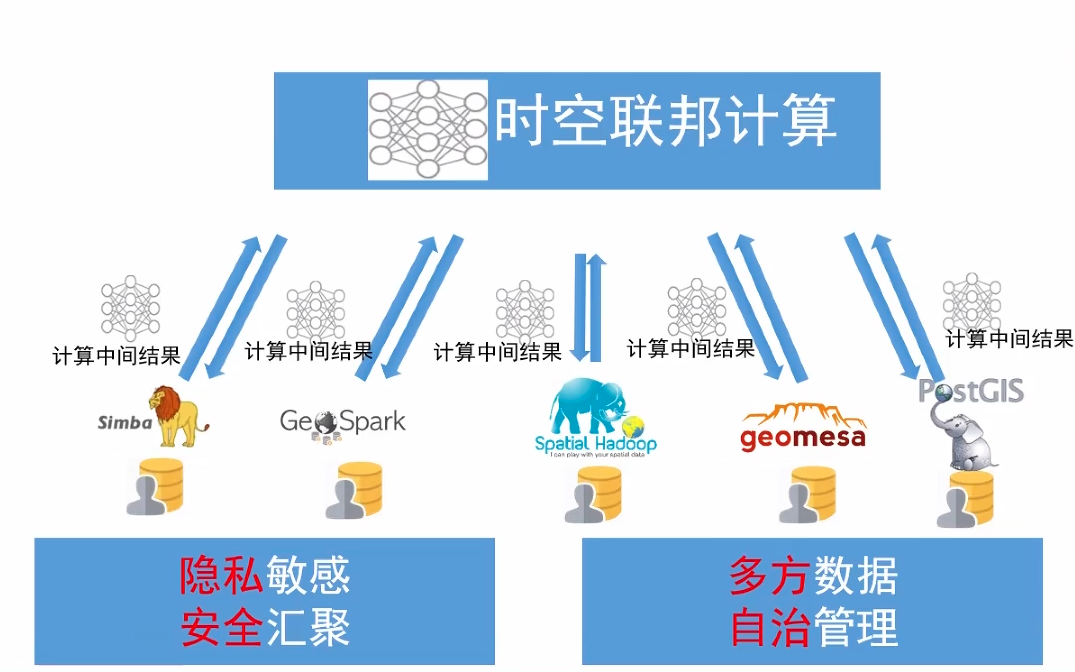
和傳統聯邦學習一樣，時空聯邦計算也可分為跨裝置（cross-device）和跨筒倉（cross-silo）兩種。跨裝置型別中參與方為邊緣裝置，在我們此處的時空資料探勘場景下常常是交通流量監測的感測器。而在跨筒倉的型別中參與方多為各企業或組織，在我們此處的場景下常常是各共用單車和網約車的服務商。在科研中，聯邦時空資料探勘會帶來包括但不限於下列的幾個議題：

對通訊的效率要求更高，但是問題常常具有一定的容錯性，這就允許我們採用隨機演演算法進行加速。比如一個共用單車服務商可能會頻繁處理「在地鐵站方圓2km內有多少共用單車」，然而現實中有多個共用單車服務商，為了不逐一查詢，我們可以用隨機取樣進行查詢的方法來近似查詢結果。
特別地，對於跨裝置型別而言，可能還需要考慮各節點之間的空間關係，此時往往將各個節點及其之間的空間關係建模為圖資料結構。
問題型別多樣，可能還會牽涉到組合優化、強化學習等，導致每輪迭代的聚合內容不同於普通的聯邦優化演演算法，

這裡特別提一下北京航空航天大學的童詠昕組Big Data Analysis Group，近年來他們組在聯邦學習和時空資料探勘方面做了不少工作，大家可以特別關注下。

2. 聯邦時空資料探勘經典論文閱讀

2.1 SIGKDD 2021:《Cross-Node Federated Graph Neural Network for Spatio-Temporal Data Modeling》

本篇文章的靚點在於用GRU網路學習各節點的時序資料的同時，用GNN去學習節點之間的拓撲關係資訊。雖然用GNN學習網路拓撲資訊也不是這篇論文首創了，早在2019年就有人這麼做過^[2]，但將時間和空間一起考慮據我所知確實是首次。

論文將所有節點和其網路連線視為圖\(G=(V, E)\)，節點\(i\in V\)的嵌入向量為\(v_i\)，邊\(k\in E\)的嵌入向量為\(e_k\)，圖的全域性嵌入向量為\(u\)。圖\(G\)的鄰接矩陣\(W\)由帶閾值的高斯核函數構造，滿足\(W_{i,j}=d_{i,j} \text{ if } d_{i,j} \geqslant \kappa \text{ else } 0\)，這裡\(d_{i,j} = \exp(-\frac{\text{dist}(i, j)^2}{\sigma^2})\)，\(\text{dist}(i, j)\)表示感測器\(i\)和\(j\)之間的公路網路距離，\(\sigma\)是所有距離的標準差。

每個節點\(i\)用編碼器-解碼器結構（其中編碼器和解碼器都為GRU）得到節點時序資料的預測資訊：

\[ \begin{aligned} &h_i = \text{Encoder}_i(x_i; \theta_{[i, 1]})\\ &\hat{y}_i = \text{Decoder}_i(x_i, [h_i; v_i]; \theta_{[i, 2]}) \end{aligned} \]

然後計算損失函數

\[\mathcal{l}_i=\mathcal{l}(\hat{y}_i, y), \]

這裡\(x_i\)是節點\(i\)的輸入時序資料，\(h_i\)是編碼器GRU的最後一個狀態, \(\hat{y}_i\)是預測標籤，\(\theta_{[i, 1]}\)和\(\theta_{[i, 2]}\)分別是編碼器和解碼器對應的引數。

sever將所有節點的隱藏層向量集合\(\{h_i\}_{i\in V}\)做為圖網路GN的輸入，從而得到所有節點的嵌入向量集合\(\{v_i\}_{i\in V}\)。圖網路的每一層都分為以下三步（論文共設定了兩層並採用殘差連線）：

① 計算更新後的邊\(k\)的嵌入向量：

\[e_{k}^{\prime}=\text{MLP}_e \left(e_{k}, v_{r_{k}}, v_{s_{k}}, u\right) \]

② 計算更新後的點\(i\)的嵌入向量(需要先聚合其鄰邊集合的資訊)：

\[ v_{i}^{\prime} = \text{MLP}_v \left(\text{Aggregate}_{e\rightarrow v} \left(\{e_k^{\prime} | r_k = i\}\right), v_i, u \right) \]

③ 計算更新後的全域性嵌入向量(需要先聚合所有點和所有邊的嵌入資訊)：

\[ u^{\prime} = \text{MLP}_u\left(\text{Aggregate}_{e\rightarrow u}(\{e^{\prime}_k \}_{k\in E}), \text{Aggregate}_{v\rightarrow u}({\{v_i\}}_{i\in V}), u \right) \]

對於圖網路的第一層，論文設定\(v_i=h_i\)，\(e_k=W_{r_k, s_k}\)(\(W\)為鄰接矩陣，\(r_k\)、\(s_k\)為邊\(k\)對應的兩個節點)，\(u\)為\(0\)向量。這裡將圖網路的引數記作\(\theta_{GN}\)。

綜上，該論文的演演算法每輪迭代的流程可描述如下：

(1) server執行：

等待每個節點執行\(\text{ClientUpdate}\)，得到更新後的編碼器-解碼器引數\(\theta_i\)。
對所有節點更新後的編碼器-解碼器引數集合\(\{\theta_i\}_{i\in V}\)進行聚合：
\[\overline{\theta} = \sum_{i\in V} \frac{N_i}{N}\theta_i \]
等待每個節點執行\(\text{ClientEncode}\)得到隱藏層向量\(h_i\)。
進行多輪迭代以更新圖網路引數\(\theta_{GN}\)，在每輪迭代中依次進行以下操作：
- 計算所有節點的點嵌入向量：
\[ \{v_i\}_{i\in V} = \text{GN}\left(\{h_i\}_{i\in V}; \theta_{GN} \right) \]
- 將\(\{v_i\}_{i\in V}\)發往各節點。
- 等待每個節點執行\(\text{ClientBackward}\)得到\(\nabla_{v_i} \mathcal{l}_i\)並將其發往server。
- 收集\(\{\nabla_{v_i} \mathcal{l}_i\}_{i\in V}\)，並從\(\{v_i\}_{i\in V}\)開始繼續進行反向傳播得到\(\{\nabla_{\theta_{GN}}\mathcal{l}_i\}_{i\in V}\)。
- 更新圖網路引數\(\theta_{GN}\)：
  \[\theta_{GN} = \theta_{GN} - \eta \sum_{i\in V}\nabla_{\theta_{GN}}\mathcal{l}_i \]
更新節點嵌入向量
\[ \{v_i\}_{i\in V} = \text{GN}\left(\{h_i\}_{i\in V}; \theta_{GN} \right) \]
將\(\{v_i\}_{i\in V}\)發往client。

(2) 第\(i\)個client所執行操作的具體定義如下：

\(\text{ClientUpdate}\)

進行多輪的區域性迭代以更新引數\(\theta_i\):
\[\theta_i = \theta_i - \eta \nabla_{\theta_i} \mathcal{l}_i \]
將\(\theta_i\)發往server。

\(\text{ClientEncode}\)

計算\(h_i=\text{Encoder}_i(x_i; \theta_{[i, 1]})\)並行往server。

\(\text{ClientBackward}\)

計算\(\nabla_{v_i} \mathcal{l}_i\)並行往server。

2.2 TKDE 2021:《Efficient Approximate Range Aggregation over Large-scale Spatial Data Federation》^[2]

本文討論了在聯邦場景下的空間資料聚合查詢，比如共用單車服務商就經常會處理「在地鐵站方圓2公里內有多少量共用單車」這類查詢。該演演算法在公共衛生響應、城市環境監測等領域都有廣泛的應用。

設空間物件為\(\langle l_o, a_o\rangle\)，其中\(l_o\)是空間物件的位置，\(a_0\)是相應的測量屬性，如\(l_0\)可以為計程車的GPS位置，\(a_0\)為其速度。

假定有\(K\)個client(資料筒倉)。\(O_{k}=\{o_1,o_2,\cdots,o_{n_{k}}\}\)為在第\(k\)個client中的空間物件集合，\(O\)為所有空間資料物件集合。因為論文采用橫向聯邦學習（資料劃分），滿足所有空間物件集合\(O=\bigcup_{k=1}^{K}\left\{O_{k}\right\}\)。

給定擁有空間資料物件集合\(O\)的聯邦\(S\)，一個查詢範圍\(R\)與一個聚合函數\(F\)，則我們定義一個聯邦範圍聚合(Federated Range Aggregation， FRA)查詢為：

\[Q(R, F)=F\left(\left\{a_{o} \mid o \in O, o \text { is within } R\right\}\right) \]

而對於在聯邦場景下的第\(k\)個client，則只能回答查詢\(Q\left(R, F\right)_k=F\left(\left\{a_{0} \mid o \in O_{k}, o \text { is within } R\right\}\right)\)。注意\(R\)可以是圓型或矩形的。論文的演演算法就是要去獲得查詢結果的\(Q(R,F)\)近似值（出於效率考慮不要求遍歷每個client以獲得精確值）。

若假定有兩個資料筒倉，筒倉1有10個空間資料物件，筒倉2有8個空間資料物件。則下圖展示了對座標(4,6)方圓3個座標單位內的物件屬性和進行查詢（筒倉1物件標註為藍色，筒倉2物件標註為紅色）:

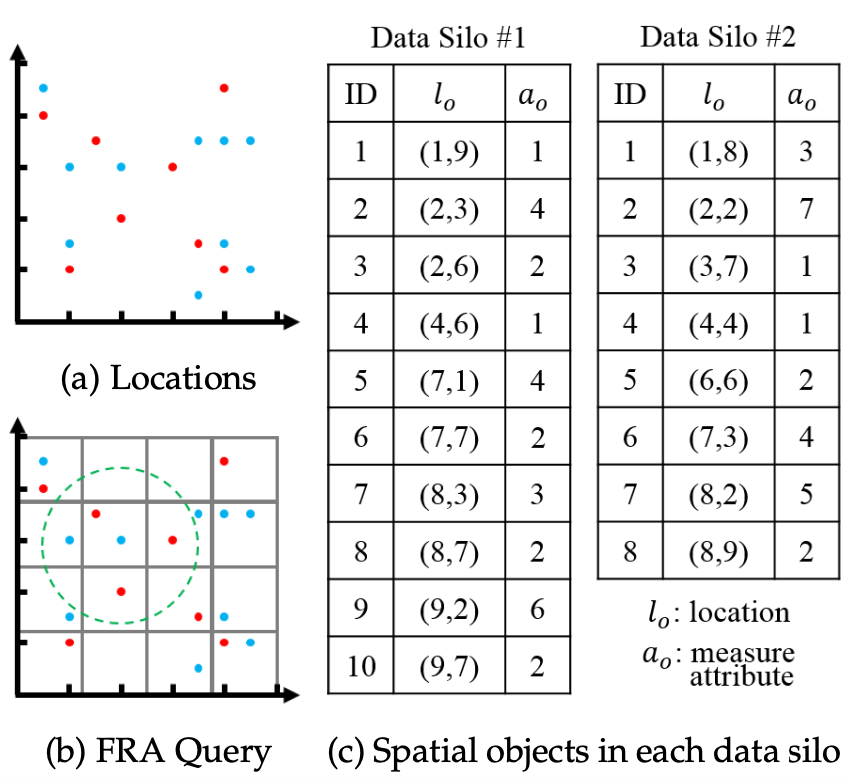
在執行聯邦查詢演演算法之前，第\(k\)個client需要先構建其中資料的網格索引集合\(g_k\)，然後將其傳送到server。server將其聚合得到\(g=\{g_1, \cdots, g_K\}\)。

然後，給定查詢範圍\(R\)，聚合函數\(F\)，則回答查詢\(Q(R, F)\)的流程可描述如下（若假定空間資料物件在不同節點間呈現IID分佈）：

隨機選取一個節點\(k\)
將\((R, F)\)傳送到節點\(k\)。
從節點\(k\)接收查詢結果\(res_k\)。
令\(sum = 0, sum_k = 0\)（前者為所有節點中物件的屬性之和，後者為第\(k\)個節點中物件的屬性之和）。
對網格索引集合\(g\)中的每一個與查詢範圍\(R\)有交集的網格\(i\)，執行：

\[\begin{aligned} & sum = sum + F(\{a_o \mid o在網格i中 \})\\ & sum_k = sum_k + F(\{a_o \mid o在網格i中且 i\in g_k \}) \end{aligned} \]
計算\(ans = res_k \times( sum /sum_k)\)
返回\(ans\)

回到上面圖中的例子，假定隨機採中的節點為\(silo \#2\)。演演算法依次遍歷左上角的\(3\times 3\)網格，計算出所有節點中空間物件的屬性之和\(sum=4+0+0(\text{first row})+2+2+4(\text{second row})+4+1+4(\text{third row})=21\)，節點2中空間物件的屬性之和\(sum_2 = 3+0+0+0+1+2+0+1+4=11\)，而節點2中在\(R\)範圍內的空間物件屬性之和\(res_2=1+2+1=4\)，則可得到範圍\(R\)所有物件屬性和的近似計算結果\(4 \times (21/11)=7.6\)。

其中，論文在節點\(k\)的本地查詢過程中提出一種特殊的稱為LSR-Forest的索引技術，為每個資料筒倉加速了原生的範圍聚合查詢。

整體演演算法流程描述如下：

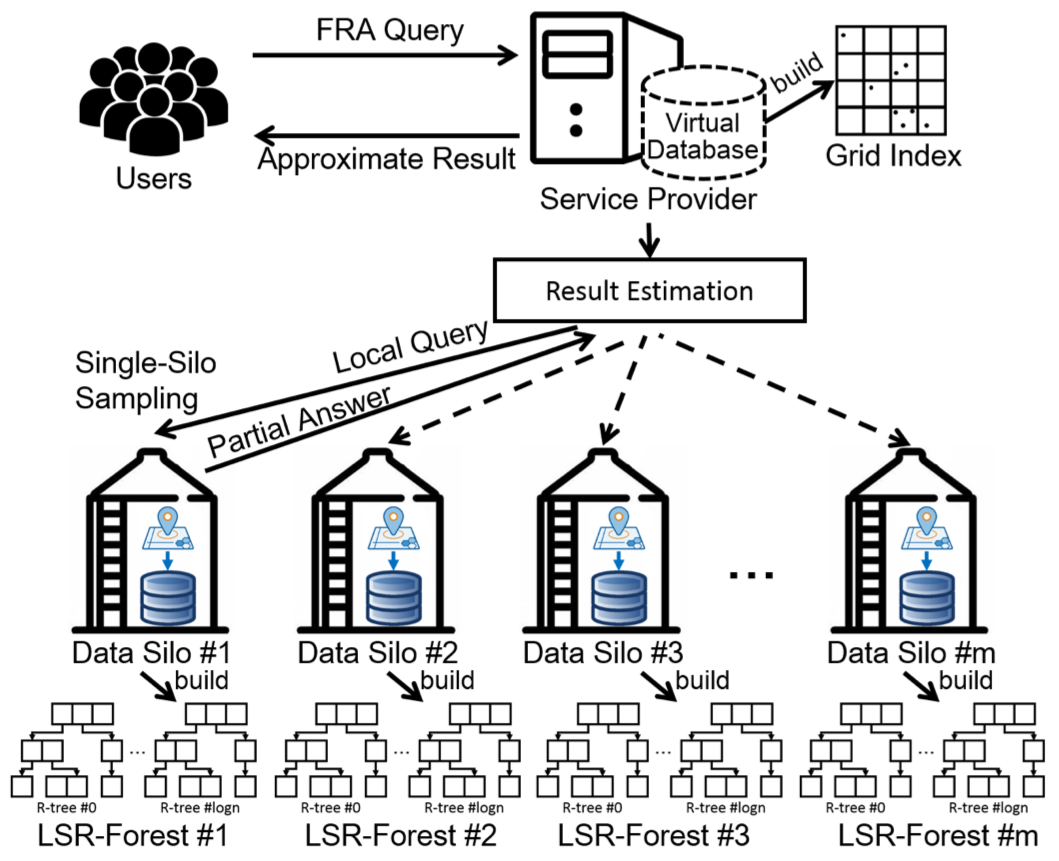
不過上述演演算法假定空間資料物件在不同節點間呈現IID分佈，這樣才能直接從來自某個隨機節點的查詢結果\(res_k\)（論文中稱為partial answer，可視為一種有偏估計）推出所有節點的查詢結果。而對於Non-IID的情況，則需要將演演算法修改為：

隨機選取一個節點\(k\)
將查詢\((R, F)\)傳送到節點\(k\)。
從節點\(k\)接收查詢結果\(res_k^1,\cdots, res_k^{|g_k|}\)（其中\(res_k^i\)表示\(k\)節點內\(i\)網格中的物件屬性和）。
令\(ans^{\prime} = 0\)。
對網格索引集合\(g\)中的每一個與查詢範圍\(R\)有交集的網格\(i\)，執行：

\[\begin{aligned} & est^i = res_k^i\times \frac{F(\{a_o | o在網格i中 \})}{F(\{a_o | o在網格i中且 i\in g_k \})} \\ & ans^{\prime} = ans^{\prime} + est^i \end{aligned} \]
返回\(ans^{\prime}\)

2.3 KDD 2022:《Fed-LTD: Towards Cross-Platform Ride Hailing via Federated Learning to Dispatch》^[3]

本篇論文旨在解決跨平臺叫車問題，即多平臺在不共用資料的情況下協同進行訂單分配。本文的靚點在於將原本用於求解多時間步二分圖最大匹配問題的強化學習演演算法擴充套件到聯邦場景下，同時結合MD5+區域性敏感性雜湊保證了資料的隱私性。

設\(U\)為司機集合，\(u\in U\)表示一個司機，\(u.loc\)為該司機的位置（用網格座標表示）; \(V\)為訂單集合，\(v\in V\)表示一個訂單，\(v.origin\)和\(v.destination\)分別為乘客目前位置和目的地位置，\(v.reward\)為訂單的收入。司機和使用者集合能夠形成一個二分圖\(G=(U\cup V, E)\)，這裡每條邊\(e=(u, v)\in E\)都有對應權重\(w(u, v)=v.reward\)。當\(u.loc\)和\(v.origin\)之間的距離超過閾值\(R\)時邊會被截斷。

定義\(\mathcal{M}\)是一個在二分圖\(G\)上的匹配結果，該匹配結果為司機-訂單對的集合，其中每個元素\((u, v)\)滿足\(u\in U, v \in V\)且\(u\)和\(v\)只在\(\mathcal{M}\)中出現一次。我們定義以下功效函數做為\(\mathcal{M}\)中的邊權和：

\[\text{SUM}(\mathcal{M}(G))=\sum_{(u, v) \in \mathcal{M}} w(u, v) \]

給定二分圖\(G\)，找到能夠最大化\(\text{SUM}(\mathcal{M}(G))\)的匹配結果\(\mathcal{M}\)是經典的二分圖最大匹配問題，可以用匈牙利演演算法在多項式時間內求解。不過在實際的訂單分配場景下，訂單和司機都是以線上（online）的形式到達的，基於批次處理的模型在這種場景下被廣泛應用。若給定批次序列\(\langle 1,2, \cdots, T\rangle\)，在\(t\)時刻待匹配的司機和訂單形成二分圖\(G^t\)，此時訂單分配問題可以定義如下：

\[\max \sum_{t=1}^{T} \text{SUM} \left(\mathcal{M}^{t}\left(G^{t}\right)\right) \]

最樸素的方法是為每個批次分別進行二分圖最大匹配。不過，在大規模歷史資料的幫助下，基於強化學習的方法能夠取得更好的效果。

我們將司機視為智慧體，他們的地理位置視為狀態，選定接下某個訂單或保持空閒為動作，價值函數為在特定狀態的期望累積獎勵：

\[\mathcal{V}(s^t) = \mathbb{E}[\sum_{t} r^t |s^t] \]

這裡\(s^t\)是狀態向量，\(r^t\)是第\(t\)個批次的獎勵和。價值函數按照Bellman方程來更新：

\[\mathcal{V}\left(s^{t}\right) \leftarrow \mathcal{V}\left(s^{t}\right)+\alpha \cdot \sum_{u}\left(r_{u}^{t}+\gamma \mathcal{V}\left(s_{v}^{t+1}\right)-\mathcal{V}\left(s_{u}^{t}\right)\right) \]

這裡\(u\)和\(v\)分別是司機和訂單，\(\alpha\)是學習率，\(\gamma\)是折扣因子。然後，分配決策可以由各個參與方基於學得的價值來決定。

\[w(u, v)=v.reward+\gamma \mathcal{V}\left(s_{e}^{t+1}\right)-\mathcal{V} \left(s_{u}^{t}\right) \]

在對二分圖的邊權進行更新後，就能夠使用匈牙利演演算法來求解本地分配決策問題了。

具體在聯邦場景下，正如local SGD有其聯邦版本FedAvg，這裡的基於強化學習的Learning-to-Dispatch(LTD)方法也有其對應的聯邦版本Fed-LTD，演演算法每輪迭代（對應一個批次）的流程可描述如下：

(1) 第\(k\)個client節點執行：

更新\(\mathcal{V}_k\):

\[\mathcal{V}_k^{\prime}\left(s^{t}\right) = \mathcal{V}_k\left(s^{t}\right)+\eta \cdot \sum_{u}\left(r_{u}^{t}+\gamma \mathcal{V}_k\left(s_{v}^{t+1}\right)-\mathcal{V}_k\left(s_{u}^{t}\right)\right) \]

計算\(\Delta \mathcal{V}_{k} = \mathcal{V}^{\prime}_{k}-\mathcal{V}_{k}\)。
對\(\Delta \mathcal{V}_k\)進行編碼：\( \Delta \widetilde{\mathcal{V}}_k = \text{Encode}(\Delta \mathcal{V}_k)\)。
更新邊權：
\[w(u, v)=v . r e w a r d+\gamma \mathcal{V}\left(s_{e}^{t+1}\right)-\mathcal{V}\left(s_{u}^{t}\right) \]
執行匹配演演算法並得到\(\mathcal{M}(G_k)\)。
計算殘差二分圖\(G_{\Delta_{k}} = G_{k}-\mathcal{M}\left(G_{k}\right)\)。
對\(G_{\Delta_{k}}\)進行編碼：\(\widetilde{G}_{\Delta_{k}} = \text { EncodeRBG }\left(G_{\Delta_{k}}\right)\)。
將\(\Delta \widetilde{\mathcal{V}}_k\)，\(\widetilde{G}_{\Delta_{k}}\)傳送到server。

(2) server執行：

每\(t_d\)輪聚合一次價值：\(\mathcal{V} = \mathcal{V}+ \sum_{k=1}^{K} \Delta \tilde{\mathcal{V}}_{k}\).
對各節點殘差二分圖進行聚合：\(G_{\Delta} = \operatorname{DecodeRBG}\left(\tilde{G}_{\Delta_{1}}, \cdots \bar{G}_{\Delta_{K}}\right)\)。
執行匹配演演算法得到\(\mathcal{M}^{\prime}(G_{\Delta})\)。
將\(\mathcal{V}\)，\(\mathcal{M}^{\prime}(G_{\Delta})\)發往各client節點。

上面的演演算法描述中對\(\mathcal{\Delta V_k}\)的\(\text{Encode}\)操作為隨機掩碼(random masking)。其中殘差二分圖(residual bipartite graph, RBG)\(G_{\Delta_k}\)是指在每一輪迭代進行區域性二分圖匹配後，每個client剩下的還未匹配的節點。對\(G_{\Delta_k}\)的\(\text{EncodeRBG}\)操作為MD5+區域性敏感性雜湊(locality sensitive hashing, LSH)，還函數會生成圖節點的安全簽名；server則能夠通過\(\text{DecodeRBG}\)操作恢復殘差二分圖。

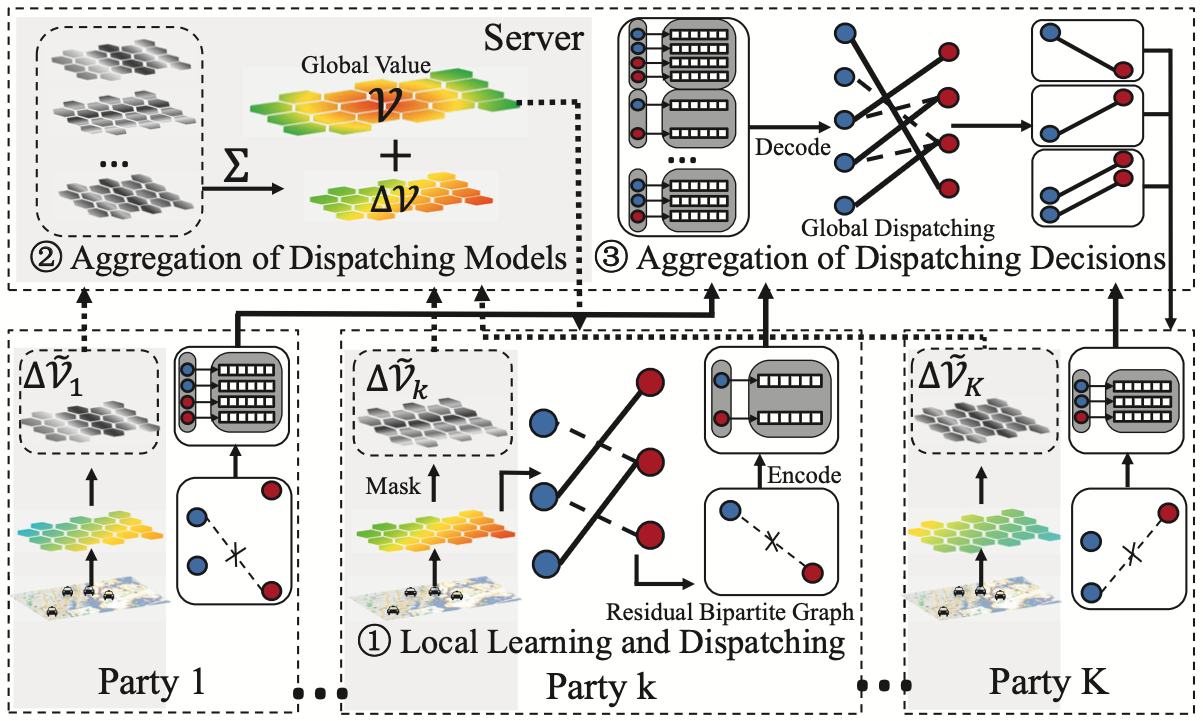
完整的演演算法流程示意圖如下：

參考

[1]
Meng C, Rambhatla S, Liu Y. Cross-node federated graph neural network for spatio-temporal data modeling[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. 2021: 1202-1211.
[2] Shi Y, Tong Y, Zeng Y, et al. Efficient Approximate Range Aggregation over Large-scale Spatial Data Federation[J]. IEEE Transactions on Knowledge and Data Engineering, 2021.
[3] Yansheng Wang, Yongxin Tong, Zimu Zhou, Ziyao Ren, Yi Xu, Guobin Wu, Weifeng Lv. "Fed-LTD: Towards Cross-Platform Ride Hailing via Federated Learning to Dispatch", in Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington D.C., USA, August 14-18, 2022.