網路流，二分圖與圖的匹配

CHANGE LOG

• 2021.12.5：更換模板程式碼。新增二分圖部分。
• 2022.1.11：重構網路流部分。新增網路流的應用與模型。
• 2022.1.1.13：新增上下界網路流部分。
• 2022.5.11：重構網路流部分，更換模板程式碼。
• 2022.6.1：重構二分圖部分，修改事實性錯誤。補充 dinic 演演算法的複雜度證明。
• 2022.7.17：新增圖的匹配部分。

1. 網路流

網路流的核心在於建圖。建圖是精髓，建圖是人類智慧。

網路流的建圖方法一定程度上刻畫了貪心問題的內在性質，從而簡便地支援了 反悔，不需要我們為每道貪心問題都尋找反悔策略。

1.1 基本定義

一個網路是一張 有向圖 \(G = (V, E)\)，對於每條有向邊 \((u, v)\in E\) 存在 容量限制 \(c(u, v)\)。特別的，若 \((u, v)\notin E\)，則 \(c(u, v) = 0\)。

網路的可行流分為有源匯（通常用 \(S\) 表示源點，\(T\) 表示匯點）和無源匯兩種，但無論哪一種，其對應的 流函數 \(f\) 均具有以下三個性質：

• 首先給出定義，流函數 \(f:(u, v)\to \R\) 是從二元 有序對 \((u, v)\) 向實數集 \(\R\) 的對映，其中 \(u, v\in V\)。\(f(u, v)\) 稱為邊 \((u, v)\) 的 流量。
• \(f\) 滿足 容量限制：\(f(u, v)\leq c(u, v)\)。每條邊的流量不能超過容量。若 \(f(u, v) = c(u, v)\)，則稱邊 \((u, v)\) 滿流。
• \(f\) 具有 斜對稱 性質：\(f(u, v) = -f(v, u)\)。\(u\to v\) 有 \(1\) 的流量，也可稱 \(v\to u\) 有 \(-1\) 的流量。
• \(f\) 具有 流量守恆 性質：除源匯點外（無源匯網路流則不存在源匯點），從每個節點流入和流出的流量相等，即 \(\forall i \neq S, T, \sum f(u, i) = \sum f(i, v)\)。每個節點 不儲存流量，流進多少就流出多少。

以下是一些網路流相關定義。

• 對於 有源匯 網路，根據斜對稱和容量守恆性質，可以得到 \(\sum f(S, i) = \sum f(i, T)\)，此時這個相等的和稱為當前流 \(f\) 的 流量。

• 定義流 \(f\) 在網路 \(G\) 上的 殘量網路 \(G_f = (V, E_f)\) 為容量函數等於 \(c_f = c - f\) 的網路。根據容量限制，我們有 \(c_f(u, v) \geq 0\)。若 \(c_f(u, v) = 0\)，則視 \((u, v)\) 在殘量網路上不存在，\((u, v)\notin E_f\)。換句話說，將每條邊的容量減去流量後，刪去滿流邊即可得到殘量網路。

• 定義 增廣路 \(P\) 是殘量網路 \(G_f\) 上從 源點 \(S\) 到 匯點 \(T\) 的一條路徑。無源匯網路流不討論增廣路。

• 將 \(V\) 分成 互不相交 的兩個點集 \(A, B\)，其中 \(S\in A\)，\(T\in B\)，這種點的劃分方式叫做 割。定義割的 容量 為 \(\sum \limits_{u\in A} \sum \limits_{v\in B} c(u, v)\)，流量 為 \(\sum\limits_{u \in A}\sum_\limits{v \in B} f(u, v)\)。若 \(u, v\) 所屬點集不同，則稱有向邊 \((u, v)\) 為 割邊。

接下來的討論大部分與有源匯網路流相關。對於無源匯網路流，見 1.5.1 小節無源匯網路流部分。

1.2 網路最大流：EK 與 dinic

網路最大流相關演演算法，最著名的是 Edmonds-Karp 和 dinic。對於更高階的 SAP / ISAP / HLPP，此處不做介紹。

給定網路 \(G = (V, E)\) 和源匯，求最大流量（Maximum flow，簡稱 MF）。

1.2.1 增廣

接下來要介紹的兩個演演算法均使用了 不斷尋找增廣路 和 能流滿就流滿 的貪心思想。

具體地，找到殘量網路 \(G_f\) 上的一條增廣路 \(P\)，併為 \(P\) 上的每一條邊增加 \(c_f(P) = \min \limits_{(u, v)\in P} c_f(u, v)\) 的流量。如果增加的流量大於該值，一些邊將不滿足容量限制，而根據能流滿就流滿的思想，增加的流量也不應小於該值。

我們在增廣的過程中儘量流滿一條增廣路，同時每條邊的流量在增廣過程中不會減少。貪心的正確性如何保證？

在為當前邊 \((u, v)\in P\) 增加 流量 \(c_f(P)\) 時，我們需要給其反邊 \((v, u)\) 的 容量 加上 \(c_f(P)\)，這樣的目的是 支援反悔，收回給出的一部分流量。體現在 \(G_f\) 上，就是新的 \(G_{f'}\) 的 \(c_{f'}(u, v)\) 相較於 \(c_f(u, v)\) 減少了 \(c_f(P)\)，而 \(c_{f'}(v, u)\) 相較於 \(c_f(v, u)\) 增加了 \(c_f(P)\)。

上述操作稱為一次 增廣。

關於增廣有一個常用技巧：成對變換。網路流建圖一般使用鏈式前向星，我們將每條邊與它的反向邊按編號連續儲存，編號分別記為 \(k\) 和 \(k+1\)，其中 \(2\mid k\)，從而快速求得 \(k\) 的反向邊編號為 \(k\ \mathrm{xor}\ 1\)。為此，初始邊數 cnt 應設為 \(1\)，這一點千萬不要忘記！

1.2.2 最大流最小割定理

在介紹 EK 和 dinic 之前，我們還需要一個貫穿網路流始終的最核心，最基本的結論：最大流等於最小割。

• 任意一組流的流量 不大於 任意一組割的容量：

  考慮每單位流量，設其經過 \(u\in A, v\in B\) 的割邊 \(u\to v\) 的次數為 \(\mathrm{to}\)，經過 \(v\to u\) 的割邊次數為 \(\mathrm{back}\)。必然有 \(\mathrm{to} = \mathrm{back} + 1\)，否則不可能從 \(S\) 流到 \(T\)。

  根據斜對稱性質與割的流量的定義，每單位流量對割邊流量之和的貢獻為 \(\mathrm{to} - \mathrm{back} = 1\)，因此網路總流量等於割邊流量之和。

  對每一種流的方案均應用上述結論，並根據容量限制，推出流的流量 \(\leq\) 割的容量。

• 存在一組流的流量 等於 一組割的容量：

  我們斷言最大流存在，此時 殘量網路不連通：若連通則可以繼續增廣，與最大流的最大性矛盾。這為我們自然地提供了一組割，使其容量等於流量，即當前可行流的流量。

綜上，結論得證。

1.2.3 Edmonds-Karp 演演算法

1.2.3.1 演演算法簡介

Edmonds-Karp 演演算法的核心是使用 bfs 尋找 長度最短 的增廣路。為此，我們記錄流向每個點的邊的編號，然後從匯點 \(T\) 不斷反推到源點 \(S\)。時間複雜度 \(\mathcal{O}(n m ^ 2)\)。

注意，任意選擇增廣路增廣，複雜度將會退化成和流量相關（樸素的 FF 演演算法），因為 EK 的複雜度證明需要用到增廣路長度最短的性質。

模板題 P3381 網路最大流 程式碼如下。

#include <bits/stdc++.h>
using namespace std;
const int N = 200 + 5, M = 5e3 + 5;
struct flow {
  long long fl[N], limit[M << 1];
  int cnt = 1, hd[N], nxt[M << 1], to[M << 1], fr[N];
  void add(int u, int v, int w) {
    nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v, limit[cnt] = w;
    nxt[++cnt] = hd[v], hd[v] = cnt, to[cnt] = u, limit[cnt] = 0;
  }
  long long maxflow(int s, int t) {
    long long flow = 0;
    while(1) {
      queue<int> q;
      memset(fl, -1, sizeof(fl));
      fl[s] = 1e18, q.push(s);
      while(!q.empty()) {
        int t = q.front();
        q.pop();
        for(int i = hd[t]; i; i = nxt[i]) {
          int it = to[i];
          if(limit[i] && fl[it] == -1) { // 剩餘流量為 0，在殘量網路上不存在，不能走
            fl[it] = min(limit[i], fl[t]); // 記錄流量
            fr[it] = i, q.push(it); // 記錄流向每個點的邊
          }
        }
      }
      if(fl[t] == -1) return flow;
      flow += fl[t];
      for(int u = t; u != s; u = to[fr[u] ^ 1]) limit[fr[u]] -= fl[t], limit[fr[u] ^ 1] += fl[t]; // 從 T 一路反推到 S，並更新每條邊的剩餘流量
    }
  }
} g;
int n, m, s, t;
int main() {
  cin >> n >> m >> s >> t;
  for(int i = 1; i <= m; i++) {
    int u, v, w;
    cin >> u >> v >> w, g.add(u, v, w);
  }
  cout << g.maxflow(s, t) << endl;
  return 0;
}

1.2.3.2 複雜度證明

為證明 EK 的時間複雜度，我們需要這樣一條引理：每次增廣後殘量網路上 \(S\) 到每個節點的最短路長度 不減。

考慮反證法，假設存在節點 \(x\) 使得 \(G_{f'}\) 上 \(S\to x\) 的最短路 \(dis'_x\) 小於 \(G_f\) 上 \(S\to x\) 的最短路 \(dis_x\)，則必然存在 \(x\) 使得在 \(G_{f'}\) 上 \(S\to x\) 的最短路上除了 \(x\) 以外的節點 \(y\) 均滿足 \(dis_y\leq dis'_y\)。設 \(y\) 是 \(G_{f'}\) 上 \(S\to x\) 的最短路上 \(x\) 的上一個節點，則 \(dis_x' = dis_y' + 1\)。

若 \((y, x)\in E_f\)，則 \(dis_x\leq dis_y + 1\)，有 \(dis_y' + 1 = dis_x' < dis_x\leq dis_y + 1\)，得出 \(dis_y' < dis_y\)，矛盾，因此有向邊 \((y, x)\) 不在原來的殘量網路 \(G_f\) 上。因為 \((y, x)\in E_{f'}\)，所以 \((x, y)\) 必然被增廣，即 \(dis_x + 1 = dis_y\)（增廣路是最短路），所以 \(dis_y' + 1 = dis_x < dis_x = dis_y - 1\)，與 \(dis_y\leq dis'_y\) 矛盾。引理證畢。

接下來證明 EK 的複雜度。

不妨設某次增廣的增廣路為 \(P\)。根據能流滿就流滿的原則，存在 \((x, y)\) 使其當前剩餘流量 \(c_f(x, y)\) 等於本次增廣流量 \(c_f(P)\)。這使得 \((x, y)\) 屬於原來的殘量網路，但不在增廣後的殘量網路上。我們稱這種邊為 關鍵邊。

因為增廣路是最短路，我們有 \(dis_x + 1 = dis_y\)。設使得 \((x, y)\) 再一次出現在增廣路徑上的增廣對應的殘量網路為 \(G_{f'}\)（增廣前）。此時 \(dis_y' + 1 = dis_x'\)，因為 \((y, x)\) 即將被增廣。

根據引理，\(dis_y' \geq dis_y\)，因此 \(dis_x' - 1 \geq dis_x + 1\)，即 \((x, y)\) 每次在殘量網路上消失又出現必然使得 \(dis_x\) 至少增加 \(2\)。

綜上，每條邊作為關鍵邊的次數不超過 \(\mathcal{O}(n)\)。因為一次增廣必然存在關鍵邊，所以總增廣次數不超過 \(\mathcal{O}(nm)\)，時間複雜度 \(\mathcal{O}(nm ^ 2)\)。

1.2.4 dinic 演演算法

1.2.4.1 演演算法介紹

dinic 演演算法的核心思想是 分層圖 以及 相鄰層之間增廣，通過 bfs 和 dfs 實現。首先 bfs 給圖分層，分層後從 \(S\) 開始 dfs 多路增廣。維護當前節點和剩餘流量，向下一層節點繼續流。

給圖分層的目的是將網路視作 DAG，規範增廣路的形態，防止流成一個環。

dinic 演演算法有重要的 當前弧優化。增廣時，容量等於流量的邊無用，可直接跳過，不需要每次搜尋到同一個點時都從鄰接表頭開始遍歷。為此，記錄從每個點出發第一條沒有流滿的邊，稱為 當前弧。每次搜尋到一個節點就從其當前弧開始增廣。

注意，每次多路增廣前每個點的當前弧應初始化為鄰接表頭，因為並非一旦流量等於容量，這條邊就永遠無用。反向邊流量的增加會讓它重新出現在殘量網路中。

當前弧優化後的 dinic 時間複雜度 \(\mathcal{O}(n ^ 2m)\)。若不加當前弧優化，時間複雜度會退化至和 EK 一樣的 \(\mathcal{O}(nm ^ 2)\)。此時由於 dfs 常數過大，實際表現並沒有 EK 優秀。

• Dinic 實際上蘊含了 EK，因為 dinic 本質也是不斷找最短路增廣。相較於 EK，dinic 使用了多路增廣和當前弧優化兩個技巧。

1.2.4.2 當前弧優化的注意點

for(int i = cur[u]; res && i; i = nxt[i]) {
  cur[u] = i;
  // do something
}

上述程式碼不可以寫成

for(int &i = cur[u]; res && i; i = nxt[i]) {
  // do something
}

因為若 \(u\to v\) 這條邊讓剩餘流量 res 變成 \(0\)，第二種寫法會使 \(u\) 的當前弧直接跳過 \((u,v)\)，但 \((u,v)\) 不一定流滿，所以不應跳過。這會導致當前弧跳過很多未流滿的邊，使增廣效率降低，從而大幅降低程式執行效率。實際表現比 EK 還要差。

另一種解決方法是在迴圈末尾判斷 if(!res) return flow;。總之，在寫當前弧優化時千萬注意不能跳過沒有流滿的邊。

模板題 P3381 網路最大流 程式碼如下。

#include <bits/stdc++.h>
using namespace std;
const int N = 200 + 5, M = 5e3 + 5;
struct flow {
  int cnt = 1, hd[N], nxt[M << 1], to[M << 1], limit[M << 1];
  void add(int u, int v, int w) {
    nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v, limit[cnt] = w;
    nxt[++cnt] = hd[v], hd[v] = cnt, to[cnt] = u, limit[cnt] = 0;
  }
  int T, dis[N], cur[N];
  long long dfs(int id, long long res) {
    if(id == T) return res;
    long long flow = 0;
    for(int i = cur[id]; i && res; i = nxt[i]) {
      cur[id] = i;
      int c = min(res, (long long) limit[i]), it = to[i];
      if(dis[id] + 1 == dis[it] && c) {
        int k = dfs(it, c);
        flow += k, res -= k, limit[i] -= k, limit[i ^ 1] += k;
      }
    }
    if(!flow) dis[id] = -1;
    return flow;
  }
  long long maxflow(int s, int t) {
    T = t;
    long long flow = 0;
    while(1) {
      queue<int> q;
      memcpy(cur, hd, sizeof(hd));
      memset(dis, -1, sizeof(dis));
      q.push(s), dis[s] = 0;
      while(!q.empty()) {
        int t = q.front();
        q.pop();
        for(int i = hd[t]; i; i = nxt[i])
          if(dis[to[i]] == -1 && limit[i])
            dis[to[i]] = dis[t] + 1, q.push(to[i]);
      }
      if(dis[t] == -1) return flow;
      flow += dfs(s, 1e18);
    }
  }
} g;
int n, m, s, t;
int main() {
  cin >> n >> m >> s >> t;
  for(int i = 1; i <= m; i++) {
    int u, v, w;
    cin >> u >> v >> w, g.add(u, v, w);
  }
  cout << g.maxflow(s, t) << endl;
  return 0;
}

1.2.4.3 複雜度證明

dinic 的複雜度證明也是一個技術活。

在證明 EK 的時間複雜度時，我們使用了一個引理，就是 \(S\) 到每個節點的最短路單調不減。因為 dinic 蘊含 EK，所以該引理仍然成立。

我們現在嘗試證明對於 dinic 的一次增廣，\(S\) 到 \(T\) 的最短路增加。

反證法，假設存在一次增廣使得 \(S\) 到 \(T\) 的最短路沒有增加。由引理，\(S\) 到 \(T\) 的最短路不變。稱其為結論 1。

考察 增廣後 的一條從 \(S\) 到 \(T\) 的最短路 \(P = \{S = p_0\to p_1 \to \cdots \to p_{k - 1} \to p_k = T\}\)，此時 \(S\to p_i\) 的最短路 \(dis'(p_i)\) 等於 \(i\)，\(S\to T\) 的最短路 \(dis'(T)\) 等於 \(k\)。

由引理，增廣前 \(S\) 到 \(p_i\) 的最短路 \(dis(p_i) \leq i\)。由結論 1，\(dis(T) = dis'(T) = k\)。

若對於所有 \(i\) 均有 \(dis(p_i) = i\)，則根據 dinic 的演演算法流程，\(P\) 在本輪增廣中被增廣。因此，\(P\) 必然存在一條邊不在增廣後的殘量網路上，這與增廣後 \(P\) 是一條從 \(S\) 到 \(T\) 的最短路矛盾，因為 \(P\) 甚至不連通。

因此，存在 \(dis(p_i) < i(0 < i < k)\)（\(k = 1\) 時可以直接匯出矛盾）。又因為 \(dis(p_k) = k\)，所以必然存在 \(x\) 和 \(x + 1\) 滿足 \(dis(p_x) + 2 \leq dis(p_{x + 1})\)，即 \((p_x, p_{x + 1})\) 不在原來的殘量網路上。

又因為增廣後 \((p_x, p_{x + 1})\) 在殘量網路上，所以 \((p_{x + 1}, p_x)\) 被增廣，即 \(dis(p_{x + 1}) + 1 = dis(p_x)\)。這與 \(dis(p_{x + 1}) - 2 \geq dis(p_x)\) 矛盾，證畢。

• 上述證明中我們沒有用到 \(T\) 的任何性質，故同理可證一輪增廣從 \(S\) 到每個點的最短路增加，前提是 \(S\) 在增廣前可達該點。

這樣，我們證明了增廣輪數為 \(\mathcal{O}(n)\) 級別。接下來考慮一輪增廣的複雜度，這部分比較好證。

對於本身就沒有流量的邊，使用當前弧優化後這些邊造成的總複雜度為 \(\mathcal{O}(m)\)，因為我們只用花 \(\mathcal{O}(1)\) 的代價跳過這些邊。

dfs 時，每次到達 \(T\) 都代表找到一條增廣路。我們將尋找這條增廣路的代價放縮至增廣路的長度，即 \(\mathcal{O}(n)\)。實際遠達不到這一上界（但仍然是 \(\mathcal{O}(n)\)。達不到上界指常數非常小），畢竟 dfs 一棵樹的複雜度不是所有葉子的深度之和，類似理解在圖上 dfs 的情況。

找到增廣路後，我們將回溯至增廣路上第一條關鍵邊（因為沒有剩餘流量了），並將所有關鍵邊的流量置為零。這些關鍵邊會在第二次遍歷到時被直接跳過，這部分，即跳過已經作為某次增廣的關鍵邊的邊的總複雜度同樣為 \(\mathcal{O}(m)\)。

只剩下增廣的複雜度還沒有計入。每條邊最多會作為一次增廣的關鍵邊，即到達 \(T\) 的次數為 \(\mathcal{O}(m)\)，因此一次增廣的複雜度為增廣複雜度和增廣路條數之積 \(\mathcal{O}(nm)\)。從分析過程即可看出這個上界非常鬆，這也是為什麼 dinic 在求解網路最大流時表現非常好。

1.3 無負環的費用流：SSP 與 Primal-Dual

費用流一般指 最小費用最大流（Minimum cost maximum flow，簡稱 MCMF）。

相較於一般的網路最大流，在原有網路 \(G\) 的基礎上，每條邊多了一個屬性：權值 \(w(x,y)\)。最小費用最大流在要求我們在 保證最大流 的前提下，求出 \(\sum_\limits{(x,y)\in E} f(x, y)\times w(x, y)\) 的最小值。

簡單地說，\(w\) 就是每條邊流 \(1\) 單位流量的費用。我們需要最小化這一費用，因此被稱為費用流。

1.3.1 連續最短路演演算法

1.3.1.1 演演算法介紹

連續最短路演演算法 Successive Shortest Path，簡稱 SSP。這一演演算法的核心思想是每次找到 長度最短的增廣路 進行增廣，且僅在網路 初始無負環 時能得到正確答案。

SSP 演演算法有兩種實現，一種基於 EK 演演算法，另一種基於 dinic 演演算法。這兩種實現均要求將 bfs 換成 SPFA（每條邊的長度即 \(w\)），且 dinic 的 dfs 多路增廣僅在 \(dis_x + w(x, y) = dis_y\) 之間的邊進行。

\(x\to y\) 在退流流過 \(y\to x\) 時費用也要退掉，所以對於原網路的每條邊 \((x, y)\)，其反邊的權值 \(w(y, x)\) 應設為 \(-w(x, y)\)。

時間複雜度 \(\mathcal{O}(nmf)\)，其中 \(f\) 為最大流流量。實際應用中此上界非常鬆，因為不僅增廣次數遠遠達不到 \(f\)，同時 SPFA 的複雜度也遠遠達不到 \(nm\)，可以放心大膽使用。

OI 界一般以 dinic 作為網路最大流的標準演演算法，以基於 EK 的 SSP 作為費用流的標準演演算法。「最大流不卡 dinic，費用流不卡 EK」是業界公約。

注意，SPFA 在隊首為 \(T\) 時不能直接 break，因為第一次取出 \(T\) 時 dis[T] 不一定取到最短路。

模板題 P3381 最小費用最大流 程式碼。

#include <bits/stdc++.h>
using namespace std;
const int N = 5e3 + 5, M = 5e4 + 5;
struct flow {
  int cnt = 1, hd[N], nxt[M << 1], to[M << 1], limit[M << 1], cst[M << 1];
  void add(int u, int v, int w, int c) {
    nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v, limit[cnt] = w, cst[cnt] = c;
    nxt[++cnt] = hd[v], hd[v] = cnt, to[cnt] = u, limit[cnt] = 0, cst[cnt] = -c;
  }
  int fr[N], fl[N], in[N], dis[N];
  pair<int, int> mincost(int s, int t) {
    int flow = 0, cost = 0;
    while(1) { // SPFA
      queue<int> q;
      memset(dis, 0x3f, sizeof(dis));
      memset(in, 0, sizeof(in));
      fl[s] = 1e9, dis[s] = 0, q.push(s);
      while(!q.empty()) {
        int t = q.front();
        q.pop(), in[t] = 0;
        for(int i = hd[t]; i; i = nxt[i]) {
          int it = to[i], d = dis[t] + cst[i];
          if(limit[i] && d < dis[it]) {
            fl[it] = min(limit[i], fl[t]), fr[it] = i, dis[it] = d;
            if(!in[it]) in[it] = 1, q.push(it);
          }
        }
      }
      if(dis[t] > 1e9) return make_pair(flow, cost);
      flow += fl[t], cost += dis[t] * fl[t];
      for(int u = t; u != s; u = to[fr[u] ^ 1]) limit[fr[u]] -= fl[t], limit[fr[u] ^ 1] += fl[t];
    }
  }
} g;
int n, m, s, t;
int main() {
  cin >> n >> m >> s >> t;
  for(int i = 1; i <= m; i++) {
    int u, v, w, c;
    cin >> u >> v >> w >> c, g.add(u, v, w, c);
  }
  pair<int, int> ans = g.mincost(s, t);
  cout << ans.first << " " << ans.second << endl;
  return 0;
}

1.3.1.2 正確性證明

我們嘗試證明每次增廣 \(S\to T\) 長度最短的增廣路，一定能求出最小費用最大流。根據最大流最小割定理可證流的最大性，因此只需證明流的費用最小性。

考慮兩個流量相等的流 \(f_1, f_2\)，令 \(\Delta f = f_2 - f_1\)，則 \(\Delta f\) 由若干個正流環組成，因其流量為零。若 \(f_1\) 的費用大於 \(f_2\)，則 \(\Delta f\) 包含至少一個正流負環，因其費用為負。

若流 \(f\) 的殘量網路包含負環，在負環上增廣可以得到流量相等但費用更小的流。相反，若流 \(f\) 不是費用最小的流，則存在流 \(f'\) 使得 \(\Delta f = f' - f\) 包含正流負環，推出 \(f\) 的殘量網路有負環。因此，\(f\) 是所有流量與之相等的流費用最小的，當且僅當 \(f\) 的殘量網路上不存在負環。

考慮歸納證明。假設增廣前 \(f\) 的殘量網路無負環，設增廣後的流為 \(f'\)。

假設存在流 \(f''\) 的流量與 \(f'\) 相等但費用更小。考察 \(\Delta f' = f' - f\)，\(\Delta f'' = f'' - f\)。因為 \(\Delta f'\) 取到 \(S\to T\) 的最短路，所以 \(\Delta f''\) 的 \(S\to T\) 的費用相較於 \(\Delta f'\) 不會更小。但 \(\Delta f''\) 的費用比 \(\Delta f'\) 小，所以 \(\Delta f''\) 存在正流負環，即 \(f\) 的殘量網路存在負環，與假設矛盾。

因此，不存在流量與 \(f'\) 相等但費用更小的流。這同時也說明了 \(f'\) 的殘量網路上無負環，推出下一輪增廣的假設成立。由於初始假設成立，所以歸納假設成立。證畢。

1.3.2 Primal-Dual 原始對偶演演算法

建議先學習 Johnson 全源最短路演演算法，詳見 初級圖論。

和 SSP 一樣，Primal-Dual 原始對偶演演算法也僅適用於 無負環 的網路。其核心為嘗試為每個點賦一個 勢能 \(h_i\)，讓原圖的最短路不變且 邊權非負。

使用 Johnson 全源最短路演演算法的思想，我們先用一遍 SPFA 求出源點到每個點的最短路 \(h_i\)，則 \(i\to j\) 的新邊權定為 \(w'_{i, j} = w_{i, j} + h_i - h_j\)。根據三角形不等式，顯然 \(w'_{i, j} \geq 0\)。因此經過上述轉化，我們可以使用更穩定的 Dijkstra 而非 SPFA 求解增廣路。

找到增廣路後，每次增廣都會改變殘量網路的形態。為此，我們用每次增廣時 Dijkstra 跑出來的最短路加在 \(h\) 上，即 \(h'_i\gets h_i+dis_i\)。正確性證明如下。

• 如果 \(i\to j\) 在增廣路上，有 \(dis_i + w_{i, j} + (h_i - h_j) = dis_j\)。由於 \(w_{i, j} = -w_{j, i}\)，所以 \(w_{j, i} + (dis_j + h_j) - (dis_i + h_i) = 0\)，即 反邊邊權為 \(0\)。
• 對於原有的邊，我們有 \(dis_i + w_{i, j} + (h_i - h_j) \geq dis_j\)，即 \(w_{i, j} + (dis_i + h_i) - (dis_j + h_j)\geq 0\)，原邊權仍然非負。

實際表現方面，Primal-Dual 相較於 SSP 並沒有很大的優勢，大概是因為 SPFA 本身已經夠快了，且堆優化的 dijkstra 常數較大。

程式碼。

1.4 對網路流的理解

1.4.1 網路流與貪心

在費用流的過程中，我們的策略是 貪心 找到長度最短的增廣路並進行增廣，但當前決策並不一定最優，因此需要為反邊新增流量，表示 支援反悔。因此，網路流本質上是 可反悔貪心，而運用上下界網路流等技巧可以很方便地處理問題的一些限制。

更一般的，網路流是一種特殊的貪心，它們之間可以相互轉化。對於具有特定增廣模式（網路具有某種性質）的網路流，可以從貪心的角度思考，從而使用資料結構維護。而大部分貪心題目也可以通過網路流解釋。

換句話說，網路流 將貪心用圖的形式刻畫，而解決網路流問題的演演算法與某種支援反悔的貪心策略相對應，這使得我們不需要為每道貪心都尋找反悔策略，相反，建出圖後就是一遍最大流或者費用流的事兒了。

1.4.2 網路流題目的技巧

網路流相關問題，關鍵在於發現 題目的每一種方案與一種流或割對應。例如在 P2057 [SHOI2007]善意的投票 一題中，直接將每個小朋友拆點不可行，因為無法考慮到他與他的朋友意見不一致時的貢獻。

為此，我們應用 最小割等於最大流 這一結論，考慮如何 用一組割來表示一種意見方案，最終得到解法。每割掉一條邊都表示付出 \(1\) 的代價，因此，將支援和反對的小朋友分別與 \(S, T\) 連邊，同時對於一對朋友，他們互相之間需要連邊，得到的圖的最小割即為所求：割掉 \(S, i\) 之間的邊表示 \(i\) 由支援變為反對，付出 \(1\) 的代價，\(i, T\) 之間類似。而若割掉兩個朋友 \(u,v\) 之間的邊，表示兩個人意見不一，因為在殘量網路上 \(u, v\) 分別與 \(S, T\) 相連。

換句話說，對於一組割，其唯一對應了一種方案，殘量網路上與 \(S\) 相連的人支援，與 \(T\) 相連的人反對。這就是經典的 集合劃分模型。

1.4.3 求方案的注意點

在應用最大流最小割定理求解問題時，剛學會網路流的同學可能會陷入一個誤區，就是最大流對應的最小割以所有在最大流中流滿的邊作為割邊。

仔細想想就會發現這是錯誤的。反例如 \(G = S\xrightarrow 1 1 \xrightarrow 1 T\)。

回想割的定義：將 \(V\) 分成兩個互不相交的點集 \(A,B\) 滿足 \(S\in A\) 且 \(T\in B\)，則所有兩端不屬於同一集合的邊才是割邊。

在求解最大流的過程中，我們時刻維護了殘量網路上 \(S\) 到每個點的距離 \(dis(u)\)。這自然地提供了一組割的方案：若 \(dis(u)\) 存在則 \(u\in A\)，否則 \(u\in B\)。結合殘量網路的定義可知割邊所有容量均流滿，再應用最大流最小割定理，可以證明這組割一定是最小割。

因此，如果一組割對應了題目的一種方案，在求解最大流之後，一定不能將所有流滿的邊視作割邊，而是將兩端所在集合不同的邊視作割邊。在解決集合劃分模型相關問題時需要格外注意這一點。

1.4.4 反悔的性質

因為網路流演演算法本身自帶反悔操作，所以在解決動態加邊的 最大流 問題時，我們不需要擔心原來的流方案會影響到演演算法求解新圖最大流時的正確性。

但對於費用流，因為其正確性依賴於每一步增廣路均為最短路，所以一旦給網路加入新邊，就必須重新跑費用流才能得到正確費用。

1.5 上下界網路流

上下界網路流相較於原始網路 \(G\)，每條邊多了一個屬性：流量下界 \(b(u, v)\)，它使可行的流函數需滿足的流量限制更加嚴格：\(b(u, v)\leq f(u, v)\leq c(u, v)\)。

1.5.1 無源匯可行流

無源匯上下界可行流是上下界網路流的基礎。我們需要為一張無源匯的網路尋找一個流函數 \(f\)，使得其滿足流量限制，斜對稱以及流量守恆限制。

解決該問題的核心思想，是 先滿足流量下界限制，再嘗試調整。具體地，我們首先讓每條邊 \((u, v)\) 都 流滿下界 \(b(u, v)\)，算出每個點的淨流量 \(w_i = \sum f(u,i) - \sum f(i, u)\)。當 \(w_i > 0\) 時，說明流到點 \(i\) 的流量太多了，還要再還出去 \(w_i\) 才能流量守恆。相反，若 \(w_i < 0\)，說明 \(i\) 還要流進 \(-w_i\) 單位流量。根據斜對稱，我們有 \(\sum w_i = 0\)，因此不妨設 \(\Delta = \sum_\limits{w_i > 0} w_i = \sum_\limits{w_i < 0} -w_i\)。

這啟發我們新建一個網路 \(G' \approx G\)，但每條邊的流量限制 \(c' = c - f = c - b\)。此外新建 獨立於原有點集 的 超級源點 \(SS\) 和 超級匯點 \(TT\)（儘管當前的 \(G\) 無源無匯，但這樣定義是為了接下來方便區分有源匯時不同最大流過程中的源點和匯點），若 \(w_i > 0\)，則 \(SS\to i\) 連容量為 \(w_i\) 的邊，否則從 \(i\to TT\) 連容量為 \(-w_i\) 的邊。不難發現從 \(SS\) 連出了總容量為 \(\Delta\) 的邊，且總容量為 \(\Delta\) 的邊連向了 \(TT\)。

若 \(SS\to TT\) 的最大流不等於 \(\Delta\)，說明我們找不到一種合法方案，使得在滿足 流量限制 的前提下具有 流量守恆 性質。相反，若等於 \(\Delta\)，則 \(f_\mathrm{cur}(u, v) = b(u, v) + f'(u, v)\) 顯然合法，因為此時每個點的 \(w_i\) 均為 \(0\)，流量守恆，且 \(f_{\rm cur} = b + f' \leq b + c' = b + (c - f) = b + (c - b) = c\)，即 \(b\leq f_{\rm cur} \leq c\)。

程式碼。

1.5.2 有源匯可行流

從 \(T\to S\) 連容量為 \(+\infty\) 的邊，轉化為 無源匯 上下界可行流。注意連邊是 源匯 之間而非 超源超匯。

1.5.3 有源匯最大流

有源匯上下界最大流演演算法基於一個非常有用的結論：給定 任意 一組 可行流，對其執行最大流演演算法，我們總能得到正確的最大流。這是因為最大流演演算法本身 支援復原，即退流操作。所以，無論初始的流函數 \(f\) 如何，只要 \(f\) 合法，就一定能求出最大流。

因此，我們考慮先求出任意一組可行流，再進行 初步調整：首先對網路 \(G\) 跑一遍有源匯 可行流，過程中我們會新建網路 \(G'\)。然後，撤去 \(SS, TT\) 以及 \(T\to S\) 容量為 \(+\infty\) 的邊。這是因為 \(SS, TT\) 存在的意義是求解無源匯可行流，\(T\to S\) 的邊是將有源匯可行流轉化為無源匯可行流。這說明現在我們已經得到了一組有源匯可行流，除非轉化成的無源匯可行流問題無解。若要得到當前流量，\(T\to S\) 的 反邊 \(S\to T\) 的流量即為所求。

接下來進行 二次調整。根據結論，我們只需要以 \(S\) 為源，\(T\) 為匯在 \(\color{red} G'\) 上再跑一遍最大流，並將可行流流量與最大流流量（新增流量）相加即為答案。注意與在此之前求解無源匯上下界可行流時，以 \(SS\) 和 \(TT\) 為源匯作區分。

• 易錯點 1：調整的整個過程在 \(G'\) 上進行，千萬不能在 \(G\) 上面跑最大流，因為 \(G\) 上面的退流操作會使得 \(f\) 不符合容量限制，而 \(G'\) 不會。因為 \(G\) 的實際流量 \(f\) 等於 \(b + f'\)，其中 \(f'\) 是 \(G'\) 上的流函數，所以只要 \(f'\) 符合容量限制，那麼 \(f\) 一定也符合。
• 易錯點 2：可行流流量是 \(T\to S\) 的反邊流量，而不是 \(SS\to TT\) 的流量！

程式碼。

1.5.4 有源匯最小流

根據 \(S\to T\) 的最小流等於 \(T\to S\) 的最大流的相反數這一結論，用可行流流量減掉 \(G'\) 上 \(T\to S\) 的最大流。

程式碼。

1.5.5 有源匯費用流

只需將最大流演演算法換成費用流即可，所有 \(SS, TT\) 相關的連邊代價均為 \(0\)。

初始費用為 \(\sum b(u, v)w(u, v)\)，進行初步調整時需要加上 \(SS\to TT\) 調整所產生的費用，即 \(SS\to TT\) 的最小費用最大流對應的費用，進行二次調整時也要加上產生的費用。

程式碼可參考 1.6.4 小節給出的有負環的費用流程式碼。

1.6 應用與模型

1.6.1 最小割點

通常情況下題目要求的最小割是 最小割邊，但如果問題變成刪去每個 點 \(i\) 有代價 \(w_i\)，求使得 \(S, T\) 不連通的最小代價，應該如何求解呢？

考慮應用網路流的常用技巧：點邊轉化，將每個點拆成入點 \(i_{in}\) 和出點 \(i_{out}\)，從 \(i_{in}\) 向 \(i_{out}\) 連一條容量為 \(w_i\) 的邊，表示刪去這個點，使得 \(i_{in}\) 與 \(i_{out}\) 不連通需要 \(w_i\) 的代價。對於原圖的每一條邊 \((u, v)\)，從 \(u_{out}\to v_{in}\) 連容量為 \(+\infty\) 的邊，因為我們只能刪點，而不是割掉邊。

不難發現 \(S_{out}\to T_{in}\) 的最小割即為所求。

1.6.2 集合劃分模型

集合劃分模型是網路流相關問題的常見模型，讀者需要充分掌握這部分內容。

其中 \(x_i = 0 / 1\)，\(\overline{x_i}\) 表示將 \(x_i\) 取反得到的結果。

給定 \(E\) 和 \(c\)，我們的任務就是為 \(x_i\) 選擇合適的值，使得整個和式的值最小。

我們可以為上式賦予實際意義：\(n\) 個物品，\(A, B\) 兩個集合，物品 \(i\) 分到集合 \(A\) 有代價 \(a_i\)，分到集合 \(B\) 有代價 \(b_i\)。此外，給定若干限制 \((u, v, c_{u, v})\)，表示若 \(u, v\) 不在同一集合 還需要 \(c_{u, v}\) 的代價。

建模：將 \(i\) 與 \(S, T\) 連邊，容量分別為 \(b_i, a_i\)。此外，將限制 \((u, v, c_{u, v})\) 表示為 \(u, v\) 之間容量為 \(c_{u, v}\) 的 雙向邊，得到網路 \(G\)。上述問題和 最小割 是等價的：

• \(i\) 與 \(S\) 相連，此時割開了 \(i\to T\)，表示將 \(i\) 劃分到 \(A\)，有 \(a_i\) 的代價。
• \(i\) 與 \(T\) 相連，此時割開了 \(S\to i\)，表示將 \(i\) 劃分到 \(B\)，有 \(b_i\) 的代價。
• 若 \((u, v)\) 不屬於同一集合，則 \(u\to v\) 和 \(v\to u\) 之間有一條被割開（因為 \(S, T\) 分別與 \(u, v\) 相連，如果不割開一條邊，\(S, T\) 就連通了），方向取決於 \(S\) 究竟與 \(u\) 還是 \(v\) 相連。

因此，對上述網路 \(G\) 求最小割即為所求。

接下來我們討論一些擴充套件問題：

• 當 \(a_i, b_i\) 出現負值時，普通的最大流不能得到正確結果，因為我們無法解決容量為負的最大流問題。考慮將 \(a_i, b_i\) 同時加上 \(\delta_i\)，最後再在求出的最小割中減掉 \(\sum \delta_i\)。這是因為 \(i\) 必須在選或不選 任選一種 方案，所以同時為 \(a_i, b_i\) 加上 \(\delta_i\) 對最小割的影響為 \(\delta_i\)。體現在圖上即 \(S\to i\to T\)，為了使 \(S,T\) 不連通，必須 至少割掉一條邊。同時我們也只會 恰好割掉一條邊，因為 \(x\) 不能既不與 \(S\) 連通，也不與 \(T\) 連通，這與割的定義矛盾。
• 當 \(c_{u, v}\) 出現負值時，除非所有 \(c\) 均為負值且要求代價最大化，此時所有邊權取反，否則問題不可做。取反可以通過 代價和貢獻的轉化 理解，即若代價為 \(1\)，則貢獻為 \(-1\)，一般我們希望最大化貢獻，最小化代價。
• 如果限制形如 「當 \(x\) 在集合 \(A\) 且 \(y\) 在集合 \(B\) 中有代價 \(w\)」，此時連 \(x \to y\) 權值為 \(w\) 單向邊，表示如果 \(x\) 和 \(S\) 相連且 \(y\) 和 \(T\) 相連，則需要割掉這條邊產生 \(w\) 的代價，否則 \(S\to T\) 連通。在不同集合產生代價連雙向邊本質上就是將兩種情況單獨處理，連兩條單向邊。
• 當題目要求輸出方案，見 1.4.3 小節。

1.6.3 最大權閉合子圖

一張 有向圖 \(G = (V, E)\) 的 閉合子圖 \(G'\) 定義在點集 \(V' \subseteq V\) 上。一個點集 \(V'\) 符合要求當且僅當 \(V'\) 內部每個點的 所有出邊 仍指向 \(V'\)，即點集內部每個點在有向圖上能夠到達的點仍屬於該點集。\(V'\) 的 點匯出子圖 即 \(G'\)。

最大權閉合子圖問題，即每個點 \(u\) 有點權 \(w_u\)，點集的權值為點集內每個點的權值之和。求閉合子圖的最大權值。

考慮 集合劃分模型，對於每個節點，我們可以將其劃分到 選 或 不選 的集合當中，體現在建圖上即 \(S\) 與 \(i\) 相連表示選，此時需要割開 \(i\to T\)，貢獻為 \(w_i\)，因此 \(i\to T\) 有容量 \(w_i\)，同理，\(S\to i\) 有容量 \(0\)。如果 \((u, v)\in E\)，說明若 \(u\) 分到選的集合中，\(v\) 也 必須 被分到選的集合當中，即 \(u\to v\) 有容量 \(-\infty\)。對上圖求 最大割 即可。

由於最大割是 NP-Hard 問題，所以考慮權值取相反數求最小割。對於 \(w_i \leq 0\) 的點，\(i\to T\) 的容量 \(-w_i\geq 0\)。但對於 \(w_i > 0\) 的點，\(i\to T\) 的容量 \(-w_i < 0\)。我們 不允許 最大流的求解過程中出現 負容量邊（因為筆者不知道怎麼辦，大霧）。考慮應用我們上面討論過的集合劃分模型的擴充套件問題，將 \(S\to i\) 和 \(i\to T\) 同時加上 \(w_i\)，體現在建圖上即對於 \(w_i > 0\)，\(S\to i\) 容量為 \(w_i\)，\(T\to i\) 容量為 \(0\)，最後減去所有正權點權值之和，並對所得結果 取相反數。

上述操作等價於先將所有正權點選入閉合子圖，再考慮去掉不選的正權點的貢獻。如果某個 \(w_i > 0\) 的 \(i\) 和 \(T\) 連通說明 \(i\) 不選，割掉 \(S\to i\) 後有 \(w_i\) 的代價，所以 \(S\to i\) 的容量為 \(w_i\)。

綜上，我們得到了求解最大權閉合子圖的一般演演算法：對於 \(w_i > 0\)，\(S\to i\) 連容量為 \(w_i\) 的邊。對於 \(w_i < 0\)，\(i\to T\) 連容量為 \(-w_i\) 的邊。對於 \((u, v)\in E\)，\(u\to v\) 連容量為 \(+\infty\) 的邊。設得到的網路為 \(G'\)，最終答案即 \(\left(\sum_\limits{w_i > 0} w_i\right) - \mathrm{Minimum\ Cut}(G')\)。

1.6.4 有負環的費用流

考慮運用上下界網路流將負權邊強制滿流，並令反邊 \(b(v, u) = 0\)，\(c(v, u) = c(u, v)\) 表示退流。此時，\((u, v)\) 由於 \(b(u, v) = c(u, v)\)，不會出現在 \(G'\) 中，所以不可能存在負環，即任意時刻網路無負環（\(G'\) 處理完畢後刪掉 \(T\to S\) 顯然也不可能讓網路出現負環），正確性得證。

模板題 P7173 有負圈的費用流 程式碼如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 200 + 5, M = 2e4 + N;
struct flow {
  int cnt = 1, hd[N], nxt[M << 1], to[M << 1], limit[M << 1], cst[M << 1];
  void add(int u, int v, int w, int c) {
    nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v, limit[cnt] = w, cst[cnt] = c;
    nxt[++cnt] = hd[v], hd[v] = cnt, to[cnt] = u, limit[cnt] = 0, cst[cnt] = -c;
  }
  int fl[N], fr[N], dis[N], in[N];
  pair<int, int> mincost(int s, int t) {
    int flow = 0, cost = 0;
    while(1) {
      queue<int> q;
      memset(dis, 0x3f, sizeof(dis));
      q.push(s), fl[s] = 1e9, dis[s] = 0;
      while(!q.empty()) {
        int t = q.front();
        q.pop(), in[t] = 0;
        for(int i = hd[t]; i; i = nxt[i]) {
          int it = to[i], d = dis[t] + cst[i];
          if(limit[i] && d < dis[it]) {
            dis[it] = d, fl[it] = min(fl[t], limit[i]), fr[it] = i;
            if(!in[it]) in[it] = 1, q.push(it);
          }
        }
      }
      if(dis[t] > 1e9) return make_pair(flow, cost);
      flow += fl[t], cost += dis[t] * fl[t];
      for(int u = t; u != s; u = to[fr[u] ^ 1]) limit[fr[u]] -= fl[t], limit[fr[u] ^ 1] += fl[t];
    }
  }
};
struct bounded_flow {
  int e, u[M], v[M], lo[M], hi[M], cst[M];
  void add(int _u, int _v, int w, int c) {
    if(c < 0) {
      u[++e] = _u, v[e] = _v, lo[e] = w, hi[e] = w, cst[e] = c;
      u[++e] = _v, v[e] = _u, lo[e] = 0, hi[e] = w, cst[e] = -c;
    }
    else u[++e] = _u, v[e] = _v, lo[e] = 0, hi[e] = w, cst[e] = c;
  }
  flow g;
  pair<int, int> mincost(int n, int s, int t, int ss, int tt) {
    static int w[N];
    memset(w, 0, sizeof(w));
    int flow = 0, cost = 0, tot = 0;
    for(int i = 1; i <= e; i++) {
      w[u[i]] -= lo[i], w[v[i]] += lo[i];
      cost += lo[i] * cst[i];
      g.add(u[i], v[i], hi[i] - lo[i], cst[i]);
    }
    for(int i = 1; i <= n; i++)
      if(w[i] > 0) g.add(ss, i, w[i], 0), tot += w[i];
      else if(w[i] < 0) g.add(i, tt, -w[i], 0);
    g.add(t, s, 1e9, 0);
    pair<int, int> res = g.mincost(ss, tt);
    cost += res.second;
    flow += g.limit[g.hd[s]];
    g.hd[s] = g.nxt[g.hd[s]], g.hd[t] = g.nxt[g.hd[t]];
    res = g.mincost(s, t);
    return make_pair(flow + res.first, cost + res.second);
  }
} f;
int n, m, s, t;
int main() {
  cin >> n >> m >> s >> t;
  for(int i = 1; i <= m; i++) {
    int u, v, w, c;
    cin >> u >> v >> w >> c, f.add(u, v, w, c);
  }
  pair<int, int> res = f.mincost(n, s, t, 0, n + 1);
  cout << res.first << " " << res.second << endl;
  return 0;
}

1.6.5 最大費用最大流

將所有權值取相反數轉化為最小費用最大流，根據上一部分的技巧，求解（可能）有負環的費用流。

1.7 網路流 24 題

*I. P1251 餐巾計劃問題

網路流相關問題，一個十分重要的技巧是 拆點。如果把每天僅看成一個點，我們無法區分乾淨的餐巾和髒餐巾，即乾淨的餐巾用完後還能作為髒餐巾繼續流，而不是直接流到匯點去了。

因此考慮拆點，每天晚上得到 \(S\) 流入的 \(r_i\) 條髒餐巾，每天早上向 \(T\) 流出 \(r_i\) 條幹淨餐巾，對於延遲送洗相鄰兩天晚上之間連邊，對於買毛巾 \(S\) 向每天早上連邊，對於送洗，每天晚上向其對應的得到餐巾那天早上連邊，跑最小費用最大流即可。

這題還是很巧妙的，例如通過從源點流入每天晚上所代表的節點，表示強制獲得 \(r_i\) 條髒餐巾，以及從每天早上所代表的的節點流入匯點，表示強制給出 \(r_i\) 條幹淨的餐巾。

程式碼。注意 LOJ 和洛谷輸入格式不一樣。

II. P2754 [CTSC1999] 家園 / 星際轉移問題

一艘太空船所停靠的站點隨著時間的變化而變化，這啟發我們使用 分層圖 來刻畫整個星際轉移過程。

考慮從時刻 \(t\) 擴充套件到時刻 \(t + 1\)。

容易對每艘太空船 \(S\) 求出它在 \(t\) 時刻停靠的站點 \(S(t)\) 和在 \(t + 1\) 時刻停靠的站點 \(S(t + 1)\)。\(S(t)\) 上的至多 \(h_S\) 個人可以通過這艘太空船在時刻 \(t\) 到 \(t + 1\) 之間移動到 \(S(t + 1)\)（假定太空船每到達一個站點，就往站點處卸下所有的乘客）。故考慮從 \(t\) 時刻的 \(S(t)\) 向 \(t + 1\) 時刻的 \(S(t + 1)\) 連邊，容量為 \(h_S\)。

此外，由於乘客可以在太站等待，且太空站容量無限，所以 \(t\) 時刻的 \(i\) 向 \(t + 1\) 時刻的 \(i\) 連邊，容量為 \(+\infty\)。

注意地球 \(0\) 和月亮 \(-1\) 較為特殊，每個時刻不需要為它們新建節點（建完之後發現沒有必要）。

從 \(1\) 到 \(+\infty\) 列舉答案 \(t\)，如果 \(t\) 時刻 \(0\to -1\) 的最大流不小於需要轉移的人數 \(k\)，則 \(t\) 即為所求。

注意判斷無解。兩種方法，一是並查集判連通性，二是列舉到 \(750\)，即 \((n + 2) \times k\)（雖然我也不太知道怎麼證明，詳見 連結）。

程式碼。

III. P2756 飛行員配對方案問題

二分圖最大匹配模板題。對於輸出方案，只需找到所有滿流（即剩餘流量為 \(0\)）的連在兩部圖之間的邊即可。

程式碼。

IV. P2761 軟體修補程式問題

注意到總的修補程式數量很少，所以從初始態能夠到達的態一定不會太多。狀壓 + SPFA 即可。

程式碼。

V. P2762 太空飛行計劃問題

將所有實驗和儀器抽象成點，從每個實驗向它所有需要的儀器連邊，就是最大權閉合子圖問題。

程式碼。

VI. P2763 試題庫問題

建模方法非常顯然。

我們將每道題目抽象成左部點，每個型別抽象成右部點。源點向左部點連容量為 \(1\) 的邊，每道題目向它可以屬於的型別連容量為 \(1\) 的邊，每個型別向匯點連容量為該型別所需題目數的邊。

若最大流不等於 \(m\) 則無解，否則容易根據殘量網路構造方案：若 \(u\to v\) 的邊滿流說明題目 \(u\) 屬於型別 \(v\)。

程式碼。

VII. P2764 最小路徑覆蓋問題

DAG 不交最小路徑覆蓋是網路流經典問題。

題目要求每個點都被覆蓋到，但我們其實並沒有什麼方法表示一個點被覆蓋。但注意到表示一條邊被覆蓋是容易的，這啟發我們使用點邊轉化的技巧。

將點 \(i\) 拆成入點 \(in_i\) 和出點 \(out_i\)，如果原圖上 \(u\to v\) 有邊，那麼 \(out_u\) 向 \(in_v\) 連邊。

考慮這樣建模後如何求答案。首先，因為路徑不可交，所以一個點最多有 \(1\) 入度和 \(1\) 出度。因此 \(S\to out\) 和 \(in\to T\) 的流量應該均為 \(1\)。

將初始路徑條數看成 \(n\)，每流滿一條 \(out_u\to in_v\) 的邊就減少了一條路徑，因為它將 \(u\) 所在路徑和 \(v\) 所在路徑連了起來。所以我們希望儘可能多地匹配左右兩部點。

跑一遍二分圖最大匹配，得到流量 \(f\)，則 \(n - f\) 就是最小路徑覆蓋的條數。兩部點之間流滿的邊就是所有被選進路徑覆蓋的邊。設選中邊集為 \(E\)，從 \(E\) 中入度為 \(0\) 的點開始 dfs 即可求出每條路徑。

程式碼。

VIII. P2765 魔術球問題

由於按編號從小往大放，所以一個球的上方的編號一定比它大。

從小到大考慮每個球 \(i\)，如果 \(j < i\) 且 \(i + j\) 是完全平方數，那麼 \(j\) 向 \(i\) 連邊。這樣問題就轉化為了 DAG 最小路徑覆蓋。

直接做即可。如果加入 \(i\) 時 DAG 最小路徑覆蓋超過 \(n\)，則答案為 \(i - 1\)。

程式碼。

*IX. P2766 最長不下降子序列問題

一道還不錯的題目，至少筆者沒有想出來。以下用 LIS 代指最長不下降子序列。

對於第一問，我們有經典的方法，就是設 \(f_i\) 表示長為 \(i\) 的 LIS 的結尾最小值。這樣可以做到 \(\mathcal{O}(n\log n)\)，但是並不方便擴充套件到第二和第三小問。

那我們嘗試換一種 DP 方法，迴歸最原始的狀態設計，設 \(f_i\) 表示以 \(a_i\) 結尾的 LIS 最長長度。暴力轉移
\(f_i = \max\left(0, \max_\limits{j < i \land a_j\leq a_i} f_j\right) + 1\) 的複雜度是平方，對於本題而言已經可以接受了。

這樣有什麼好處呢？我們發現一個至關重要的性質，在任何最長 LIS 當中，第 \(i\) 個出現的位置的 \(f\) 值一定是 \(i\)。若非，通過反證法很容易匯出矛盾。

因此，為保證選出的 LIS 是最長的，我們只需保證任意相鄰兩個位置 \(x, y\) 都有 \(f_x + 1 = f_y\)。

通過上述分析，我們的網路流模型就呼之欲出了。為保證一個位置只被選擇一次，我們拆點後將入點向出點連容量為 \(1\) 的邊。\(S\) 向所有 \(f_i = 1\) 的 \(in_i\) 連邊，所有 \(f_i = ans\) 的 \(out_i\) 向 \(T\) 連邊，容量均為 \(1\)，對該網路求解最大流即為第二問的答案。

對於第三問，只需將 \(S\to in_1\)，\(in_1 \to out_1\)，\(in_n\to out_n\) 和 \(out_n\to T\) 的容量設為無窮大即可。這裡有兩個注意點，一是當 \(n = 1\) 的時候需要特判，否則流量無窮大。二是 \(out_n\to T\) 在 \(f_n\neq ans\) 的時候不存在。

程式碼。

X. P2770 航空路線問題

題目等價於找到從 \(1\) 到 \(n\) 的兩條只在端點處相交的路徑，使得它們的長度之和最大。

根據一個點只能被經過一次的限制，自然考慮拆點。\(1\) 和 \(n\) 的 \(in, out\) 之間連容量為 \(2\) 的邊，剩下點的 \(in, out\) 之間連容量為 \(1\) 的邊。若 \(i\) 與 \(j(i < j)\) 在原圖有邊，那麼從 \(out_i\) 向 \(in_j\) 連容量為 \(1\) 的邊。有解當且僅當 \(in_1 \to out_n\) 的最大流等於 \(2\)。

為最大化路徑長度之和，我們使每個點被流過時產生貢獻 \(1\)，求最大費用最大流。因為只會從編號小的點向編號大的點連邊，所以網路無環，可直接將費用取反求最小費用最大流。

\(n = 1\) 需要特判，不過資料好像沒有。

本題也可以 DP 求解：設兩條路徑當前端點分別在 \(i, j\) 時長度之和的最大值為 \(f_{i, j}\)。列舉 \(k > \max(i, j)\)，若 \(i, k\) 有邊則可轉移到 \(f_{k, j}\)；若 \(j, k\) 有邊則可轉移到 \(f_{i, k}\)。若 \(i, j\) 均與 \(n\) 直接相連則可用 \(f_{i, j} + 1\) 更新答案。初始值 \(f_{1, 1} = 1\)。為輸出方案，需記錄每個狀態的決策點。時間複雜度 \(\mathcal{O}(n ^ 3)\)。

程式碼。

XI. P2774 方格取數問題

相鄰格有限制的網格問題，一般都是通過黑白染色轉化到二分圖相關問題。本題就是很明顯的二分圖最大權獨立集。

程式碼。

XIII. P3254 圓桌問題

二分圖多重匹配模板題。

自然想到用一滴流量代表一個人，建圖方式就很顯然了。\(S\) 向每個代表團連容量為 \(r_i\) 的邊，每個代表團向每張餐桌連容量為 \(1\) 的邊，每張餐桌向 \(T\) 連容量為 \(c_i\) 的邊。

若最大流不等於 \(\sum r_i\) 說明無解，否則根據代表團與餐桌之間的連邊構造方案即可。

程式碼。

XIV. P3355 騎士共存問題

題圖提示我們對網格圖黑白染色，有限制的兩個格子之間顏色不同。二分圖最大獨立集直接做。

程式碼。

XV. P3356 火星探險問題

挺無聊的一道題。

首先拆點 \(in, out\) 點權轉邊權，然後一個石塊只能被採集一次，那麼若某個位置上有石塊，則 \(in \to out\) 連一條容量為 \(1\)，代價為 \(1\) 的邊，再連一條容量為 \(car - 1\)，代價為 \(0\) 的邊。

跑一遍最大費用最大流，無環所以直接費用取反 MCMF。輸出方案就記錄每個位置有多少向右和向下的流量，從 \((1, 1)\) 開始進行 \(car\) 遍 dfs 即可。

程式碼。

XVI. P3357 最長 k 可重線段集問題

由於會出現平行於 \(y\) 軸的線段，相當於閉區間 \([x, x]\)，所以直接套用最長 k 可重區間集的做法不太可行。

稍作修補，拆點 \(in_x\) 和 \(out_x\)，所有 \((l, r)\) 連 \(out_l \to in_r\)，\([x, x]\) 則是 \(in_x\to out_x\)。此外 \(in_x\to out_x\) 還要連容量為 \(k\)，代價為 \(0\) 的邊。

發現拆點還是有些麻煩，直接令 \(in_x = 2x\)，\(out_x = 2x + 1\) 即可轉化為最長 k 可重區間集。

\(m = \mathcal{O}(n)\)，程式碼。

*XVII. P3358 最長 k 可重區間集問題

如果一組方案符合條件，那麼一定能用不超過 \(k\) 條鏈把所有區間串起來，滿足每條鏈上的區間兩兩不交。相反，顯然任何能用 \(k\) 條鏈串起來的區間集合均符合要求。

因此考慮用 \(k\) 條鏈將區間串起來。為限制每個區間只能貢獻一次，將區間拆點 \(L_i\) 和 \(R_i\)，\(L_i\) 向 \(R_i\) 連容量為 \(1\)，代價為 \(r_i - l_i\) 的邊。此外，若 \(r_i \leq l_j\)，則從 \(R_i\) 向 \(L_j\) 連一條容量為 \(1\)，代價為 \(0\) 的邊。

\(S\) 向 \(L\)，\(R\) 向 \(T\) 連容量為 \(1\)，代價為 \(0\) 的邊。注意為限制流量 \(\leq k\) 需要新建 \(T'\) 然後 \(T\to T'\) 連容量為 \(k\)，代價為 \(0\) 的邊。最大費用最大流即為所求，因為連邊不成環所以直接權值取反求最小費用最大流。

\(m = \mathcal{O}(n ^ 2)\)，不是很優秀。

但實際上我們發現，我們建出的大部分邊都用於連線兩個不相交的區間。轉換一下思路，將每個座標而不是區間看成點，這樣只需在相鄰兩個點之間連邊即可描述所有連線兩個不相交的區間的邊。

具體地，將區間所有端點離散化，從小到大依次為 \(x_1, x_2, \cdots, x_k\)。令 \(x_0 = 0\)。對於所有 \(0\leq i < k\)，\(i\) 向 \(i + 1\) 連容量為 \(k\)，代價為 \(0\) 的邊，\(0\to 1\) 的邊限制了最大流 \(\leq k\)。此外，對於所有區間 \([l, r]\)，令其端點分別為 \(x_i = l\) 和 \(x_j = r\)，則 \(i\to j\) 連容量為 \(1\)，代價為 \(r - l\) 的邊。

此時我們做到了 \(m = \mathcal{O}(n)\)。程式碼。

XVIII. P4009 汽車加油行駛問題

設 \(f_{i, j, k}\) 表示走到 \((i, j)\) 且油箱剩餘 \(k\) 單位的最小代價，dijkstra 即可。放在網路流 24 題裡顯得很奇怪。

令 \(m = n ^ 2k\)，時間複雜度 \(\mathcal{O}(m\log m)\)。程式碼。

XIX. P4011 孤島營救問題

注意到鑰匙種類很少，所以將每個鑰匙種類是否擁有壓成一個 mask，bfs 即可。

時間複雜度 \(\mathcal{O}(nm2 ^ P)\)。程式碼。

XX. P4012 深海機器人問題

和 XV 火星探險一樣，用建平行邊的方式限制一條邊的權值只貢獻一次。建圖方式顯然，從所有源點向所有匯點跑最大費用最大流即可。程式碼。

XXI. P4013 數位梯形問題

通過拆點連容量為 \(1\) 的邊限制每個點只能被選一次，邊的容量設定為 \(1\) 限制每條邊只能被選一次。程式碼。

XXII. P4014 分配問題

二分圖最小 / 大權完美匹配模板題，程式碼。

XXIII. P4015 運輸問題

除了邊的容量改變，剩餘部分和上道題一模一樣，程式碼。

XXIV. P4016 負載平衡問題

類似上下界費用流，需要的貨物從源點送，多出的貨物送到匯點。

求出平均值 \(avg\)，若 \(a_i < avg\) 則 \(S\to i\) 連容量 \(avg - a_i\)，邊權為 \(0\) 的邊。否則 \(i\to T\) 連容量 \(a_i - avg\)，邊權為 \(0\) 的邊。相鄰點連容量 \(+\infty\)，邊權為 \(1\) 的邊，最小費用最大流。程式碼。

1.8 例題

現在你已經對網路流的基本原理有了一定了解，就讓我們來看一看下面這些簡單的例子，把我們剛剛學到的知識運用到實踐中吧。

I. P2936 [USACO09JAN] Total Flow S

最大流模板題。

II. P1345 [USACO5.4] 奶牛的電信 Telecowmunication

有向圖點邊轉化基礎練習題。

*III. P2057 [SHOI2007] 善意的投票 / [JLOI2010] 冠軍調查

集合劃分模型，分析見 1.4.2 小節。程式碼。

IV. P2045 方格取數加強版

有向圖點邊轉化，將每個點 \(i\) 拆成 \(i_{in}\) 和 \(i_{out}\)，\(i_{in}\to i_{out}\) 分別連容量為 \(1\)，邊權為 \(c_i\) 和容量為 \(k - 1\)，邊權為 \(0\) 的邊，表示每個點的貢獻只會算一次。每個點的出點向右側和下側點的入點連邊。\((1, 1)_{in}\to (n, n)_{out}\) 的最小費用最大流即為所求。程式碼。

V. P3410 拍照

最大權閉合子圖板子題。

VI. P2805 [NOI2009] 植物大戰殭屍

對於每個植物，從它的攻擊位置向它連邊，表示若選擇攻擊位置則必須選擇該植物。

因為環以及能到達環的點都不可以選擇，所以對反圖拓撲排序。對遍歷到的節點求解最大權閉合子圖問題。程式碼。

VII. P2604 [ZJOI2010] 網路擴容

第一問建容量 \(w\) 費用 \(0\) 的邊跑最大流，第二問新建容量 \(+\infty\) 費用 \(c\) 的邊跑限制流量 \(k\) 的費用流。程式碼。

VIII. CF1082G Petya and Graph

如果一條邊被選，則其兩個端點必須選。最大權閉合子圖模型。

IX. P5192【模板】有源匯上下界最大流

對於每一天 \(i\)，從 \(S\) 向 \(i\) 連流量限制為 \([0, D_i]\) 的邊，從 \(i\) 向每個少女 \(k_i\) 連流量限制為 \([L_{k_i}, R_{k_i}]\) 的邊。對於每個少女 \(i\)，向 \(T\) 連流量限制為 \([G_i, \infty]\) 的邊，跑有源匯上下界最大流。

注意在編號上區分 \(S, T, SS, TT\) 以及少女 \(i\) 和第 \(i\) 天。程式碼。

X. P4843 清理雪道

有源匯上下界最小流模板題。從 \(S\to i\to T\) 連容量範圍為 \([0, +\infty]\) 的邊，原圖的邊容量範圍為 \([1, +\infty]\) 表示必須被流。程式碼。

如果點邊轉化為 DAG 最小可交路徑覆蓋，則時間複雜度 \(\mathcal{O}(m ^ 3 + \mathrm{maxflow}(m , m ^ 2))\)。因為 \(m = \mathcal{O}(n ^ 2)\) 所以無法接受。

XI. P4553 80 人環遊世界

有源匯上下界費用流模板題。程式碼。

XII. P8215 [THUPC2022 初賽] 分組作業

裸的集合劃分模型。

與 \(S\) 相連表示同意，否則與 \(T\) 相連表示不同意。因此 \(S\to i\) 連權值為 \(d_i\) 的邊，\(i\to T\) 連權值為 \(c_i\) 的邊。

根據集合劃分模型，我們可以用 \(i\to j\) 權值為 \(w\) 的邊表示若 \(i\) 同意且 \(j\) 不同意，則代價加上 \(w\)。因此 \(i\) 向與其同組的人連權為 \(e_i\) 的邊。

合作是本題的一大難點，但只要想到獨立每個人的狀態和每個組的合作狀態，問題就迎刃而解了。設組 \(j\) 在最終的殘量網路上與 \(S\) 相連表示合作，與 \(T\) 相連表示不合作。

首先，如果任何人 \(i\) 不同意，其對應的組 \(j\) 均不可以合作。\(j\to i\) 連權值為 \(+\infty\) 的邊，表示如果合作且 \(i\) 不同意，則代價為 \(+\infty\)。

剩下來就好辦了。對於每個關係 \(A, B\)，\(B\) 向 \(A\) 對應的組連邊 \(a_i\)，表示若 \(B\) 同意且 \(A\) 沒有合作則有 \(a_i\) 的代價。同理，\(B\) 對應的組向 \(A\) 連邊 \(b_i\)，表示若 \(B\) 合作且 \(A\) 不同意則有 \(b_i\) 的代價。

對上述網路跑最大流即可。程式碼。

*XIII. P2053 [SCOI2007] 修車

如果技術人員 \(i\) 倒數第 \(j\) 個維修的車子是 \(k\)，將對答案產生 \(\dfrac{jT_{k, i}} n\) 的貢獻。\(\dfrac 1 n\) 是定值，可以忽略。

考慮將每個技術人員拆成 \(N\) 個點 \((i, j)(1\leq j\leq N)\)，表示技術人員 \(i\) 的倒數第 \(j\) 次維修。因為一次只能維修一輛車子，且每輛車子只會被維修一次，所以建出二分圖，左部點表示一次維修，右部點表示一輛車子，\((i, j) \to k\) 連容量為 \(1\)，費用為 \(jT_{k, i}\) 的邊。最小費用最大流即為所求。

XIV. P2153 [SDOI2009] 晨跑

將 \(2\sim n\) 拆點後跑最小費用最大流即可。

*XV. CF103E Buying Sets

沒有 \(|N(S)| = |S|\) 的限制就是裸閉合子圖模型。由於任意 \(k\) 個子集的並 \(\geq k\)，所以只需保證 \(|N(S)|\leq |S|\)。考慮為元素的權值減去 \(+\infty\)，子集的權值加上 \(+\infty\)。這樣，當 \(|N(S)| > |S|\) 時，\(+\infty\) 貢獻了至少一次，劣於不選任何一個子集，這種情況必然不會發生。

對上述模型跑最大權閉合子圖即可。程式碼。

XVI. P1231 教輔的組成

模型顯然，將中間點拆點連容量為 \(1\) 的邊限制每個中間點的度數，跑最大流即可。程式碼。

XVII. P1361 小 M 的作物

考慮集合劃分模型。

令作物與 \(S\) 相連表示種在 \(A\) 地，與 \(T\) 相連表示種在 \(B\) 地。因集合劃分模型只能處理最小化代價，故先將所有貢獻加入，嘗試最小化扣除貢獻。據此，\(S\to i\) 容量 \(a_i\)，\(i\to T\) 容量 \(b_i\)。

對於聯合貢獻，同樣先將貢獻 \(c_1 + c_2\) 加入並最小化扣除貢獻。易知 \(S\to c_A\) 容量 \(c_1\)，\(c_A \to I\) 容量 \(+\infty\)，\(I\to c_B\) 容量 \(+\infty\)，\(c_B \to T\) 容量 \(c_2\)，其中 \(I\) 為涉及到的作物集合。程式碼。

XVIII. P4313 文理分科

考慮集合劃分模型。

令學生與 \(S\) 相連表示選理科，與 \(T\) 相連表示選文科。對所有貢獻求和，嘗試最小化減去的代價。據此，\(S\to (i, j)\) 容量為 \(science_{i, j}\)，\((i, j)\to T\) 容量為 \(art_{i, j}\)。

對於聯合貢獻，新建點 \(e_1 \to (x, y)\) 容量為 \(+\infty\)，其中 \((x, y)\) 為 \((i, j)\) 及與其四連通的總共五個格子，\(S\to e_1\) 容量為 \(same\_science_{i, j}\)；新建點 \((x, y)\to e_2\) 容量為 \(+\infty\)，\(e_2\to T\) 容量為 \(same\_art{i, j}\)。程式碼。

2. 二分圖

二分圖是 OI 界常見的一類圖，其延伸出的相關演演算法和模型非常廣泛。我們將看到網路流在二分圖上的廣泛應用。

2.1 定義，性質與判定

定義：設無向圖 \(G = (V, E)\)，若能夠將 \(V\) 分成兩個點集 \(V_1\) 和 \(V_2\) 滿足 \(V_1 \cap V_2 = \varnothing\)，\(V_1 \cup V_2 = V\) 且 \(\forall (u, v) \in E\) 均有 \(u\in V_1 \land v\in V_2\)（\(\land\) 是邏輯與）或者 \(u\in V_2 \land v\in V_1\)，則稱 \(G\) 是一張二分圖，\(V_1, V_2\) 分別為其左部點和右部點。

簡單地說，二分圖就是可以將原圖點集分成兩部分，滿足兩個點集內部沒有邊的圖。這也是它的名字的由來。

有了定義，我們自然希望對其進行判定。考慮滿足條件的圖有什麼性質。

我們發現，從一個點開始，每走一條邊就會切換一次所在集合。這說明從任意一個點出發，必須經過偶數條邊才能回到這個點，即圖上不存在奇環。反過來，若一張圖不存在奇環，對其進行黑白染色就可以得到一組劃分 \(V_1, V_2\) 的方案。

綜上，我們得到判定二分圖的充要條件：不存在奇環。

• 什麼是黑白染色？我們希望給每個點染上白色或黑色，使得任意一條邊兩端的顏色不同。

  從某個點開始深搜，初始點的顏色任意。遍歷當前點 \(u\) 的所有鄰居 \(v\)。如果 \(v\) 未被存取，則將 \(v\) 的顏色設為與 \(u\) 相反的顏色並向 \(v\) 深搜。否則檢查 \(u\) 的顏色是否與 \(v\) 的顏色不同 —— 若是，說明滿足限制；否則說明圖上存在奇環，黑白染色無解。

黑白染色給予我們在 \(\mathcal{O}(|V| + |E|)\) 的時間內判定二分圖的方法。注意圖可能不連通，此時需要從每個未被染色的節點開始對連通分量進行染色。

注意，接下來討論的二分圖均指點集劃分方案 \(V_1, V_2\) 已經確定的二分圖，而非滿足條件的 \(V_1, V_2\) 未定的二分圖。事實上，給定連通二分圖，若 \(V_1, V_2\) 之間無序，則將其劃分成兩部點的方案是唯一的。但對於非連通二分圖，方案數不唯一，因為每個連通分量安排 \(V_1', V_2'\) 的方案有兩種。本質不同的劃分方案有 \(2 ^ {c - 1}\) 種，其中 \(c\) 是連通分量個數。

2.2 二分圖的匹配

給定二分圖 \(G = (V, E)\)，若邊集 \(M \subseteq E\) 滿足 \(M\) 中任意兩條邊不交於同一端點，則稱 \(M\) 是 \(G\) 的一組 匹配，匹配的大小為 \(|M|\)。

特別的，若 \(|V_1| = |V_2|\) 且匹配 \(M\) 包含 \(|V_1|\) 條邊，則稱 \(M\) 為 完美匹配。

下文稱節點 \(u\) 被匹配當且僅當 \(M\) 存在一條邊以 \(u\) 為端點。

2.2.1 最大匹配

2.2.1.1 Hopcroft-Karp 演演算法

對於給定二分圖 \(G\)，我們希望求出邊集 \(M\) 的大小的最大值。求解該問題的經典方法是匈牙利演演算法，詳見 3.2 小節。

嘗試用網路流解決問題。一個節點最多與一條邊相連，即節點度數 \(\leq 1\)。這啟發我們從源點 \(S\) 向 \(V_1\) 每個節點連容量為 \(1\) 的邊，從 \(V_2\) 每個節點向匯點 \(T\) 連容量為 \(1\) 的邊，再加上給 \(E\) 中所有邊定向後由 \(V_1\) 指向 \(V_2\) 的容量為 \(1\) 的邊。\(S\to T\) 的最大流即最大匹配。

容易證明這樣做的正確性：我們發現每個點最多與一個點相鄰，因為限制了它到源點或匯點的流量為 \(1\)。因此，一組可行流與一組匹配一一對應，且流量等於匹配大小。

使用 dinic 求解二分圖最大匹配，時間複雜度是優秀的 \(\mathcal{O}(m\sqrt n)\)。該演演算法有它自己的名字 Hopcroft-Karp，由 John Hopcroft 和 Richard Karp 在 1973 年提出。

2.2.1.2 增廣路和交錯路

在證明 HK 求解二分圖最大匹配的時間複雜度之前，我們需要補充二分圖匹配的增廣路和交錯路的定義。

考慮匹配 \(M\)，若原圖存在一條長度為奇數的路徑 \(P = p_0 \xrightarrow{e_1} p_1 \xrightarrow{e_2} \cdots \xrightarrow{e_k} p_k(2\nmid k)\) 使得 \(e_1, e_3, \cdots, e_k \notin M\)，而 \(e_2, e_4, \cdots, e_{k - 1}\in M\)，同時 \(p_0, p_k\) 均不是 \(M\) 的任何一條邊的某個端點，則稱 \(P\) 為匹配 \(M\) 的 增廣路。

用自然語言描述，增廣路是從一個沒有被匹配的點出發，依次走非匹配邊，匹配邊，非匹配邊 …… 最後通過一條非匹配邊到達 另外一部點 當中某個沒有被匹配的點的路徑。因此，不妨欽定增廣路的方向為從左部端點走向右部端點。

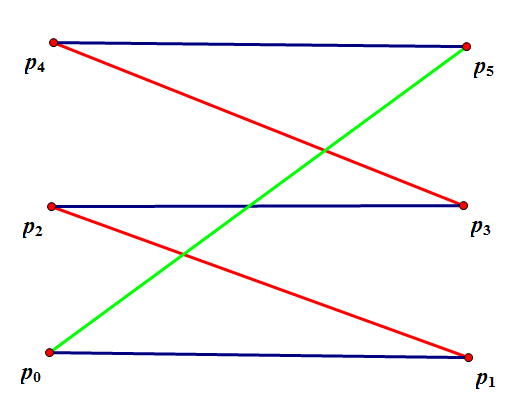
如下圖，紅色邊是匹配邊 \(M = \{(p_1, p_2), (p_3, p_4)\}\)。我們從非匹配左部點 \(p_0\) 開始，依次走非匹配邊 \((p_0, p_1)\)，匹配邊 \((p_1, p_2)\)，非匹配邊 \((p_2, p_3)\)，匹配邊 \((p_3, p_4)\) 和非匹配邊 \((p_4, p_5)\)，到達非匹配右部點 \(p_5\)。這些邊連線而成的路徑就是一條增廣路。

考察使用網路流求解二分圖最大匹配時的增廣路和二分圖匹配本身的增廣路形態，它們本質上一致：因為左部點向右部點連邊，所以對於非匹配邊，它在從左往右的方向上有流量；反之，對於匹配邊，它在從右往左的方向上有流量。

網路上增廣路的形態為從 \(S\) 開始，到某個未被匹配的左部點，然後在左右部點之間反覆橫跳，最後到達某個未被匹配的右部點，並走到 \(T\)。如果一個點被匹配，那麼在殘量網路上它和 \(S\) 或 \(T\) 不連通，因此路徑上和 \(S\)，\(T\) 相連的都是非匹配點，對應增廣路的開頭和結尾都是非匹配點。忽略掉 \(S\) 和 \(T\)，路徑的第一條和最後一條邊都是從左部點走到右部點，對應增廣路的第一條最後一條邊都是非匹配邊。

容易發現，每次將一條增廣路上所有邊的狀態取反，可得比原來匹配大 \(1\) 的匹配。

交錯路 的限制則更弱一些，它只需滿足路徑上任意相鄰兩條邊一條不在匹配內，另一條在匹配內。顯然，增廣路一定是交錯路。

2.2.1.3 複雜度證明

根據 dinic 複雜度證明的結論，每次增廣使得 \(S\to T\) 的最短路增加。因此，進行 \(\sqrt n\) 次增廣後，任意增廣路長度大於 \(\sqrt n\)。

設當前匹配為 \(P\)，最大匹配為 \(Q\)。考慮 \(P\) 和 \(Q\) 的對稱差 \(R = P\oplus Q\)，即 \(R = \{e \in E\mid [e\in P] \neq [e\in Q]\}\)。\(R\) 由若干不交的路徑和環組成，因為每個點的度數 \(\leq 2\)（\(P\) 和 \(Q\) 中每個點的度數 \(\leq 1\)）。

忽略環，因為它是由 \(P\) 和 \(Q\) 當中的邊依次交替組成的長度為偶數的環，若非則 \(P\) 或 \(Q\) 存在點度數 \(\geq 2\)，不合法。因此，將環上 \(P\) 的邊替換為 \(Q\) 的邊不會使匹配大小增加。

同理可證長度為偶數的路徑不會使匹配大小增加。

每條長度為奇數的路徑對應一條 \(P\) 上的增廣路，因為這樣的交錯路徑必然由 \(Q\) 作為第一條和最後一條邊。若以 \(P\) 作為開頭和結尾，那麼對於 \(Q\)，將該路徑上的所有邊狀態取反可以得到更大的匹配，與 \(Q\) 的最大性矛盾。因此，對 \(P\) 進行該條增廣路的增廣可以使其大小增加 \(1\)。

由於路徑不交且增廣路長度至少為 \(\sqrt n\)，所以增廣路條數不超過 \(\sqrt n\)，這說明 \(|Q| - |P| \leq \sqrt n\)。因此再增廣至多 \(\sqrt n\) 輪即可得到最大匹配。

根據每條邊的容量為 \(1\) 容易證明一輪增廣的複雜度為 \(\mathcal{O}(m)\)，因此 HK 的複雜度即 \(\mathcal{O}(m\sqrt n)\)。

上述證明結合了 「dinic 每輪增廣使得增廣路長度增加」 和 「長度 \(\geq k\) 的不交增廣路至多有 \(\dfrac n k\) 條」 兩條結論以及根號分治的思想。

2.2.2 最大多重匹配

多重匹配指節點 \(u\) 不能與超過 \(L_u\) 條邊相連。一般匹配即 \(L_u = 1\) 的特殊情況。

求解最大多重匹配，只需將 \(S\to V_1\) 的每條邊 \(S\to u\) 的容量設為 \(L_u\)，對於 \(V_2 \to T\) 同理。二分圖內部每條邊的容量不變，仍為 \(1\)。對上述網路求最大流即最大多重匹配。

HK 演演算法的時間複雜度證明中並沒有用到與 \(S, T\) 相連的邊容量為 \(1\) 的性質，因此使用 HK 求解二分圖最大多重匹配的時間複雜度仍為 \(\mathcal{O}(m\sqrt n)\)。

2.2.3 帶權最大匹配

對於最小權最大匹配，將最大流演演算法換成最小費用最大流。

對於最大權最大匹配，將最大流演演算法換成最大費用最大流。圖中無正環，只需權值取反求最小費用最大流。

對於最大權 完美 匹配，有專門的 KM 演演算法 解決該問題。詳見 3.3 小節。

2.3 二分圖相關問題

2.3.1 最小點覆蓋集

給定二分圖 \(G = (V, E)\)，若點集 \(C\subseteq V\) 滿足對於任意 \((u, v)\in E\) 都有 \(u\in C\) 或 \(v\in C\)，則稱 \(C\) 是 \(G\) 的 點覆蓋集。即一個點可以覆蓋以該點為端點的邊，覆蓋所有邊的點集就是點覆蓋集。點覆蓋集的大小為 \(|C|\)。

考慮一組點覆蓋集，不存在邊 \((u, v) \in E\) 使得 \(u, v\) 同時不屬於 \(C\)。因為一個點只有屬於 \(C\) 和不屬於 \(C\) 兩種狀態，這啟發我們將其套入集合劃分模型。

但是這樣會產生問題：一般集合劃分模型只能處理 \(x, y\) 在不同集合時產生代價的限制，不能強制某兩個點不同時在相同集合。

不過注意到我們還沒有使用 \(G\) 是二分圖的性質。因為任意一條邊連線兩部點，所以嘗試將一部點的狀態取反，即左部點與 \(S\) 連通表示它不屬於 \(C\)，但右部點與 \(S\) 連通表示它屬於 \(C\)。這樣限制變為 「如果左部點 \(u\) 與 \(S\) 連通，\(u, v\) 之間有連邊，但右部點 \(v\) 與 \(T\) 連通，則 \(u, v\) 同時不屬於 \(C\)，不合法」。

相比求解最大匹配時建出的網路，上述操作進行的修改僅是將兩部點之間連邊的容量設為 \(+\infty\)。對該網路求解最大流，可得最小點覆蓋集大小。同樣，可以根據集合劃分模型的結果求出具體最小點覆蓋集方案。

進一步地，因為一個點最多流入或流出一單位流量，所以將兩部點之間連邊的容量設為 \(1\) 不影響最終結果。這個觀察證明了最大匹配等於最小點覆蓋集。

最小點覆蓋集的應用：對於每條限制 \(lim\) 恰有兩種方案 \(u, v\) 能滿足。一種方案可滿足多條限制。求最少需要選擇多少種方案以滿足所有限制。問題可以轉化為二分圖最小點覆蓋集進行求解。

2.3.2 König 定理

如果從匹配的角度理解點覆蓋集，「不存在增廣路」 這一性質使得我們可以根據最大匹配構造出最小點覆蓋集。

以下討論基於不存在增廣路的最大匹配 \(M\)。

從任意一個未被匹配的 右部點 出發走交錯路，並依次標記所有經過的點。換言之，我們按遍歷順序依次標記從沒有匹配的右部點開始的所有交錯路上的所有點。注意，交錯路可能退化成單點。

首先確定這些交錯路的形態。交錯路必然是從右部點出發，通過非匹配邊走到左部點，再通過匹配邊走到右部點，以此類推。這說明 從左到右走匹配邊，從右到左走非匹配邊。

取出所有被標記的左部點和未被標記的右部點，我們斷言它是最小點覆蓋集。證明如下：

考慮一條匹配邊。它不可能是右端點先被標記：交錯路從右部非匹配點開始，所以右端點的標記由另外一個被標記的左部點走到它而產生。又因為從左到右走匹配邊，所以右端點和兩條匹配邊相連，矛盾。因此，它必然左端點先被標記，接下來走到右端點使得它被標記；或者兩個端點同時未被標記。一條匹配邊恰有一個端點屬於點覆蓋集。

考慮一條非匹配邊。不可能出現它的左端點未被標記且右端點被標記的情況，因為此時可以從右到左走該非匹配邊使得左端點被標記。因此一條非匹配邊至少有一個端點屬於生成的點覆蓋集。

綜上，我們證明了點覆蓋集的合法性，每一條邊被至少一個點覆蓋。點覆蓋集的最小性只需證明 \(|C|\) 取到了下界。

首先證明 \(|C| = |M|\)：

• 對於左部被標記的點，若它是非匹配點，考慮使得它被標記的交錯路，發現這是一條增廣路，矛盾。因此，被標記的左部點是匹配點。
• 對於右部點，若它是非匹配點，我們必然標記它，因為它可以作為交錯路的開頭：要麼它是孤立點，此時交錯路退化成單點；要麼存在至少一條從它出發的非匹配邊，考慮非匹配點的定義可得。因此，未被標記的右部點是匹配點。

結合上述兩點以及一條匹配邊恰有一個端點屬於點覆蓋集，匹配邊與點覆蓋集內的點一一對應。命題 \(|C| = |M|\) 得證。

而 \(|C| \geq |M|\) 非常容易證明：任何一條匹配邊都需要一個單獨的點以覆蓋它，所以任何點覆蓋集大於任何匹配。這樣，我們證明了點覆蓋集的最小性。

綜上，通過上述方法構造出的 \(C\) 是最小點覆蓋集。這是匈牙利數學家柯尼希（D.König）在 1913 年給出的構造。

König 定理：二分圖的最大匹配大小等於最小點覆蓋集大小。

2.3.3 最大獨立集

給定二分圖 \(G = (V, E)\)，若點集 \(I \subseteq V\) 滿足任意兩點不直接相連，則稱 \(I\) 是 \(G\) 的 獨立集，獨立集大小為 \(|I|\)。

考慮集合劃分模型，限制形如不存在邊 \((u, v)\in E\) 使得 \(u, v\) 同時屬於 \(I\)，和最小點覆蓋集的限制「不存在邊 \((u, v) \in E\) 使得 \(u, v\) 同時不屬於 \(C\)」恰好相反。

這啟發我們考慮 \(G\) 的點覆蓋集 \(C\) 並取反。因為每條邊至少被一個 \(u \in C\) 所覆蓋，所以 \(I = V \backslash C\) 的所有點之間互不相連。這說明獨立集與點覆蓋集 一一對應，且它們的交為空，併為 \(V\)，即點覆蓋集與獨立集互補。

綜上，二分圖最大獨立集等於 \(V\) 減去最小點覆蓋集。

2.3.4 最大團

給定二分圖 \(G = (V, E)\)，若其 點匯出子圖 \(G' = (V', E')\) 滿足對於任意 \(u, v\in V'\)，其中 \(u\in V_1\)，\(v\in V_2\)，均有 \((u, v)\in E'\)，則稱 \(G'\) 是 \(G\) 的 團。

• 作為補充，一般圖的團定義為其完全子圖。

同樣，二分圖最大團問題可以通過集合劃分模型解決。方法類似，細節不再贅述。

整個過程本質等價於求補圖最大獨立集：考慮 \(G\) 的補圖 \(G_c = (V, E_c)\)，若 \((u, v) \in E_c\) 則 \(u, v\) 不能同時出現在最大團中。故二分圖最大團等於補圖最大獨立集。

2.3.5 某部點的極值

存在一些題目讓我們求使得某部點的數量儘可能多的最小點覆蓋集，最大獨立集或最大團。

套入集合劃分模型，總可以將問題轉化為：對於二分圖 \(G\)，我們希望在維持被割掉的總邊數等於最大匹配數不變的前提下，儘可能多地割掉 \(S\) 與左部點之間的連邊，或者右部點與 \(T\) 之間的連邊。兩種情況對稱，接下來只討論前者。

• 例如，若希望使最大團左部點儘量多，根據最大團 \(\sim\) 補圖最大獨立集 \(\sim\) 補圖最小點覆蓋集的補集，我們希望使補圖最小點覆蓋集左部點儘量少。因為最小點覆蓋集的集合劃分模型形如被割掉的左部點加入覆蓋集（已經討論過這一點），所以我們希望被割掉的左部點儘量多。

如果僅在原圖上跑最大流，我們無法控制某部點被割掉的數量。此時，集合劃分模型就要發揮它的威力了。

考慮改變每個點劃分入各個集合的代價，以給予每個點被割掉的優先順序：將 \(S\) 與左部點之間的邊的容量修改為 \(c\)，右部點與 \(T\) 之間的邊容量修改為 \(c + 1\)，兩部點之間的容量設為 \(+\infty\)，這樣可以優先割掉 \((S, u\in V_1)\)。

為了保證割掉總邊數的正確性，\(c\) 應當不小於 \(n = \min(|V_1|, |V_2|)\)：不能出現割掉 \(x\) 個左部點不劣於割掉 \(y < x\) 個右部點的情況，即 \(n\times c\) 必須要大於 \((n - 1)(c + 1)\)，化簡得到 \(c > n - 1\)。這保證了我們在該網路上求得的最小割滿足割邊條數最小，而最小割邊條數就是最大匹配數。

2.4 應用與模型

2.4.1 DAG 最小路徑覆蓋

給定 DAG \(G = (V, E)\)，定義其 路徑覆蓋 為路徑集合 \(P\)，滿足每個節點至少被一條路徑覆蓋。根據路徑是否可交，即一個節點是否只能恰好被一條路徑覆蓋，可以分為不交路徑覆蓋與可交路徑覆蓋。

最小 不交 路徑覆蓋：見網路流 24 題 VII.

最小 可交 路徑覆蓋：

一個點的出度和入度可能大於 \(1\)，直接沿用不交路徑覆蓋的方法不可行。但我們發現，如果一條路徑覆蓋了某個點，那麼可以選擇佔用這個點的入度或出度，也可以選擇不佔用。這給予我們初步想法：若一條路徑真實地覆蓋了某個點，可以選擇視為沒有覆蓋。此時可能出現一條路徑兩個相鄰的被覆蓋的點在原圖上不相鄰的情況。

接下來具體描述上述思考。

考慮一組可交路徑覆蓋方案，依次考慮其中的每個路徑 \(P_i\)。稱 \(P_i\) 覆蓋點 \(u\) 當且僅當 \(u\in P_i\) 且 \(u\notin P_j(1\leq j < i)\)，即 \(u\) 第一次被覆蓋是被 \(P_i\) 覆蓋。

設 \(P_i\) 覆蓋的點集為 \(V_i\)。若 \(V_i\) 為空，則刪去 \(P_i\) 後不影響合法性，因此 \(V_i\) 非空。考慮按拓撲序將 \(V_i\) 內所有點排序，得到 \(p_1, p_2, \cdots, p_k(k = |V_i|)\)，顯然 \(p_i\) 可達 \(p_{i + 1}\)，設對應路徑為 \(P'_i\)。

一個點在路徑集合 \(\{P'_i\}\) 當中至多有 \(1\) 出度和 \(1\) 入度，再根據 \(p_i\) 可達 \(p_{i + 1}\)，考慮求出原 DAG 傳遞閉包，再對傳遞閉包求最小不交路徑覆蓋。簡單地說，若 \(i \rightsquigarrow j\)，則 \(i\) 向 \(j\) 連邊。

容易證明傳遞閉包的一組不交路徑覆蓋對應若干原圖的可交路徑覆蓋。儘管方案不唯一，因為傳遞閉包上相鄰兩點在原 DAG 上之間可能有多條路徑，但路徑條數是不變的。

綜上，DAG 最小可交路徑覆蓋是它傳遞閉包的最小不交路徑覆蓋。

2.5 例題

I. P2055 [ZJOI2009] 假期的宿舍

將所有需要住下的人視為左部點，所有空的床視為右部點。

對於左部點，源點向所有要在學校住下的人連邊。對於右部點，所有回家的人向匯點連邊。兩部點之間認識的人連邊，檢查最大匹配是否與左部點個數相等。程式碼。

II. P3701 主主樹

對於左邊能打敗右邊的，連容量為 \(1\) 的邊。左部點從 \(S\) 連容量為生命值的邊，右部點向 \(T\) 連容量為生命值的邊。注意每個 J 的生命值還要加上所屬陣營中 YYY 的數量。求出帶權最大匹配對 \(m\) 取 \(\min\)。程式碼。

III. P6268 [SHOI2002] 舞會

二分圖最大獨立集模板題，需要先對可能不連通的圖進行黑白染色。答案為 \(n\) 減去最小點覆蓋，即 \(n\) 減去最大匹配。程式碼。

IV. P7368 [USACO05NOV] Asteroids G

一個小行星被消除當且僅當它所在的行或列被選中，建出二分圖，則題目轉化為二分圖最小點覆蓋集，跑最大匹配即可。程式碼。

V. CF1684G Euclid Guess

為使得餘數為 \(t\)，除數 \(b\) 必然 \(> t\)，不妨令 \(b = t + 1\)。因為 \(a > b\)，所以 \(a\) 最小為 \(2t + 1\)。因此若存在 \(2t + 1 > m\) 則無解。

考慮接下來的過程。若 \(1\leq k < t\)，則 \((2t + k, t + k) \to (t + k, t) \to (t, k)\)，這意味著如果要搞出一個 \(t\)，我們還需要一些比較小的數作為墊背。

當 \(k = t\) 時，整個過程 \((3t, 2t)\) 只會形成一個數 \(t\)，很棒，唯一的問題是需要滿足 \(3t \leq m\)。

這樣一來就有了大致思路。找到所有 \(3t > m\) 的 大 \(t\)，我們需要一個 \((2t + k, t + k)\) 消滅掉這個 \(t\)，並且還需要 \(k\) 以及 \((t, k)\) 後續形成的數作為墊背。如果存在方案使得每個數夠用，那麼剩下來所有 \(3t\leq m\) 的 小 \(t\) 可以每次用 \((3t, 2t)\) 消滅掉。

問題轉化為怎麼消滅掉較大的 \(t\)。如果直接嘗試列舉其對應的 \(k\) 等於某個小 \(t\)，由於一次操作會涉及多個小 \(t\)，我們沒有辦法解決這種情況。

考察歐幾里得演演算法本身，我們發現對於一開始的 \((a, b)\) 而言，\(\gcd(a, b)\) 一定會出現在序列當中。這就好辦了啊！如果 \(k\) 不是 \(t\) 的約數，那麼令 \(k\gets \gcd(k, t)\) 顯然一定更優，因為後者涉及到的數完全包含於前者。更勁爆的是，後者僅涉及到 \(k\) 本身一個數。

綜上，列舉大 \(t_i\) 和小 \(t_j\)，若 \(t_j \mid t_i\) 且 \(2t_i + t_j \leq m\)，則 \(i\to j\) 連邊。大 \(t\) 之間由於 \(3t > m\) 所以內部不會連邊，跑二分圖最大匹配。如果所有左部點均被匹配則有解，將匹配對應的方案輸出，並將剩下來的小 \(t\) 通過 \((3t, 2t)\) 消滅掉，否則無解。

時間複雜度 \(\mathcal{O}(n ^ {2.5})\)，程式碼。

VI. CF1139E Maximize Mex

因每個學生恰屬於一個社團，所以一個學生可以看成其對應社團與能力值之間的連邊。對於單組詢問，只需從小到大列舉 \(i\)，若僅考慮 \(\leq i\) 的能力值時，最大匹配等於 \(i + 1\)，說明 \(\mathrm{mex}\) 可以等於 \(i + 1\)，繼續列舉 \(i + 1\)，否則說明無法使得答案大於 \(i\)，且可以使得答案等於 \(i\)，故 \(i\) 即為所求。

刪去學生不好考慮，倒過來變成加邊，根據單調性用指標維護答案即可。程式碼。

3. 圖的匹配

匹配 是一組沒有公共點的邊集，每個點要麼有唯一匹配的點，要麼是非匹配點。

乍一看，一般圖最大匹配似乎和一般圖最大獨立集同樣棘手，以至於筆者很長一段時間都以為一般圖最大匹配是 NPC 問題，但事實並非如此。

3.1 相關定義

上一章我們介紹了二分圖匹配，將相關概念遷移至一般圖上，可得如下定義：給定圖 \(G\)，

• 稱邊集 \(M\) 為 \(G\) 的一組 匹配，當且僅當 \(M\) 中任意兩條邊沒有公共點。
• 匹配的 大小 為邊數 \(|M|\)。
• 若 \(|M|\) 最大，則稱 \(M\) 為 最大匹配。最大匹配不一定唯一。
• 邊帶權時，若邊權和最大，則稱 \(M\) 為 最大權匹配。最大權匹配不一定是最大匹配。
• 若一條邊在 \(M\) 中，則稱該邊為 匹配邊，反之稱為 非匹配邊。
• 若一個點是 \(M\) 中某條邊的端點，則稱該點為 匹配點，反之稱為 非匹配點。
• 若基於 \(M\) 無法再增加匹配邊，則稱 \(M\) 為 極大匹配。極大匹配不一定最大。
• 若 \(G\) 的每個點均為匹配點，則稱 \(M\) 為 完美匹配。

資訊競賽常見匹配問題由兩個因素劃分為四類。根據圖是否是二分圖以及邊是否帶權，分為二分圖 / 一般圖最大（權）匹配。接下來將依次介紹解決它們的常用演演算法。

3.2 二分圖最大匹配

使用 Hopcroft-Karp 求解二分圖最大匹配，時間複雜度 \(\mathcal{O}(m\sqrt n)\)。

另一種常見方法是匈牙利演演算法，時間複雜度 \(\mathcal{O}(nm)\)，比 HK 劣，但它是學習 KM 演演算法的基礎。

由 2.2.1.2 小節可知將增廣路上邊的狀態取反可得比原來大 \(1\) 的匹配。

考慮反轉的過程，令增廣路為 \(p_1 \to p_2 \to \cdots \to p_{2k}\)，原 \((p_{2i}, p_{2i + 1})(1 \leq i < k)\) 是匹配邊，現 \((p_{2i - 1}, p_{2i})(1 \leq i \leq k)\) 是匹配邊。反轉後相比反轉前多出兩個匹配點，而原匹配點不會因此變為非匹配點。只要一個點被匹配，那麼它一直被匹配下去。

因此，考慮依次新增每一個左部點 \(u\in V_1\)，使用 dfs 求出是否存在從 \(u\) 開始的增廣路。若存在，則反轉增廣路上所有邊的狀態，並令匹配數 \(+1\)。設當前搜尋到的左部點為 \(x\)，具體流程如下：

• 若 \(x\) 已被存取，返回增廣失敗的資訊。
• 標記 \(x\) 已被存取。
• 遍歷 \(x\) 所有出邊對應的右部點 \(y\in N(x)\)：
  • 若 \(y\) 已被存取，則跳過。
  • 否則，若 \(y\) 為非匹配點，令 \(y\) 匹配 \(x\)，並返回增廣成功的資訊。
  • 否則，搜尋 \(y\) 匹配的左部點 \(x'\)。若成功增廣，據分析，\(y\) 匹配點左部點應變為 \(x\)，並返回增廣成功的資訊。
• 若此時仍未返回，說明 \(x\) 的所有出邊均無法增廣，返回增廣失敗的資訊。

進一步地，因每個左部點 \(x\) 最多隻會被其匹配的右部點 \(y\) 存取到，故無需記錄每個左部點是否被存取。

增廣成功次數之和即為最大匹配。注意，每次嘗試從 \(u\) 開始找增廣路前需清空存取標記。

因為每次嘗試增廣最壞情況下需遍歷所有 \(m\) 條邊，故總複雜度為 \(\mathcal{O}(nm)\)。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 500 + 5;
int n, m, E, mch[N], vis[N];
vector<int> e[N];
bool dfs(int id) {
  for(int it : e[id]) {
    if(vis[it]) continue;
    vis[it] = 1;
    if(!mch[it] || dfs(mch[it])) return mch[it] = id, 1;
  }
  return 0;
}
int main() {
  ios::sync_with_stdio(0);
  cin >> n >> m >> E;
  for(int i = 1; i <= E; i++) {
    int u, v;
    cin >> u >> v;
    e[u].push_back(v);
  }
  int ans = 0;
  for(int i = 1; i <= n; i++) {
    memset(vis, 0, sizeof(vis));
    ans += dfs(i);
  }
  cout << ans << endl;
  return 0;
}

3.3 二分圖最大權完美匹配

給定二分圖 \(G = (V, E)\)，若邊集 \(M \subseteq E\) 滿足 \(M\) 中任意兩條邊不交於同一端點，\(|M| = |V_1| = |V_2|\) 且 \(M\) 的邊權和最大，則稱 \(M\) 是 \(G\) 的一組 最大權完美匹配。將 \(|M| = |V_1| = |V_2|\) 的限制去掉，則稱 \(M\) 是 \(G\) 的一組 最大權匹配。

最大權匹配不一定是完美匹配，如下圖，最大權匹配為 \(20\)，最大權完美匹配為 \(3\)。

3.3.1 理論分析

著名的 KM 演演算法用於求解二分圖最大權 完美 匹配。若不存在完美匹配，則 KM 演演算法會死迴圈，故初始需對二分圖進行特殊處理：

• 若求最大權匹配，則補點使得兩部點大小相等，並將不存在的邊補 \(0\)。
• 若邊權可以為負，則將不存在的邊視為 \(-\infty\)。

KM 演演算法的核心步驟由線性規劃引出，但筆者不瞭解線性規劃，故直接給出結論，將顯得不自然。待筆者學習線性規劃後再做補充。

給每個點賦頂標。設左部點頂標為 \(A_i\)，右部點頂標為 \(B_j\)，需滿足對於任意邊 \((i, j)\) 均有 \(w_{i, j} \leq A_i + B_j\)。

結論：令滿足 \(w_{i, j} = A_i + B_j\) 的邊 \((i, j)\) 構成 相等子圖，若相等子圖存在完美匹配，則其為原二分圖最大權完美匹配。

證明：求得最大權完美匹配的權值為當前頂標和。對於其它完美匹配，因 \(w_{i, j} \leq A_i + B_j\)，故其權值不大於當前頂標和。證畢。

考慮在一組合法頂標基礎上調整頂標，不斷擴大相等子圖直到其存在完美匹配。類似匈牙利，列舉每個左部點 \(u\)，嘗試將其加入匹配。

從 \(u\) 出發找相等子圖的增廣路。若發現增廣路，則將路徑上邊的狀態取反，宣告成功匹配 \(u\)；否則需要對部分節點的頂標進行調整。因無增廣路，故相等子圖上所有從 \(u\) 出發的路徑均為兩端為左部點的交錯路，這些交錯路形成 交錯樹（儘管它並不是樹）。

考慮邊 \((x, y)\)，設 \(x\) 的頂標變化量為 \(\Delta_x\)，\(y\) 的頂標變化量為 \(\Delta_y\)。若 \((x, y)\) 在交錯樹上，則 \(\Delta_x + \Delta_y = 0\)，因為不應使已經進入相等子圖的邊離開相等子圖。據此可知大致調整思路：令交錯樹上左部點頂標變化量和右部點頂標變化量互為相反數。

根據 \(\Delta_x + \Delta_y \geq w_{x, y} - A_x - B_y\) 可知，

• 若增加交錯樹上左部點頂標，減少右部點頂標，令變化量為 \(d\)，\(d\geq 0\)，則
  • 對於左部點屬於交錯樹，右部點不屬於交錯樹的邊 \((x, y)\)，因 \(\Delta_x = d\) 且 \(\Delta_y = 0\)，故 \(\Delta_x + \Delta_y \geq 0\)，必然合法。
  • 對於左部點不屬於交錯樹，右部點屬於交錯樹的邊 \((x, y)\)，因 \(\Delta_x = 0\) 且 \(\Delta_y = -d\)，故 \(d\) 不大於所有 \((x, y)\) 的 \(A_x + B_y - w_{x, y}\) 的最小值。令 \(d\) 取最大值 \(d_{\max} = \min\limits_{(x, y)} (A_x + B_y - w_{x, y})\)，容易發現可將至少一條 \((x, y)\) 加入相等子圖。
  • 對於左右部點均屬於或均不屬於交錯樹的邊，無影響。
• 同理，若減少交錯樹上左部點頂標，增加右部點頂標，令變化量為 \(d\)，則 \(d\) 不大於所有左部點屬於交錯樹，右部點不屬於交錯樹的邊 \((x, y)\) 的 \(A_x + B_y - w_{x, y}\) 的最小值，且可以將至少一條這樣的 \((x, y)\) 加入相等子圖。

哪種方法更優秀呢？感性理解，加入左部點屬於交錯樹，右部點不屬於交錯樹的邊更優。增廣路以右部點結尾，所以加入這樣的邊可延伸以 \(x\) 結尾的交錯路徑（儘管不一定能找到增廣路，如當 \(y\) 為匹配點時）。但加入左部點不屬於交錯樹，右部點屬於交錯樹的邊時，無法擴大交錯樹：\(y\) 為右部點且其匹配左部點非 \(x\)，故 \((x, y)\) 是否在相等子圖中對交錯樹無影響。

綜上，不斷將交錯樹上左部點頂標增加 \(d\)，右部點頂標減少 \(d\)，可不斷往交錯樹中加入左部點屬於交錯樹，右部點不屬於交錯樹的邊 \((x, y)\)。接下來證明它一定能求出相等子圖完備匹配：

不妨設按編號從小到大依次嘗試加入每個左部點。考慮歸納法，假設前 \(i - 1\) 個左部點均可通過調整頂標加入相等子圖匹配。

考慮嘗試加入第 \(i\) 個點時不斷加邊的過程終態，所有與原交錯樹上前 \(i\) 個左部點相鄰的右部點 \(y\) 及它們之間的所有邊 \((x, y)(1\leq x \leq i)\) 均被加入交錯樹。對原二分圖執行匈牙利演演算法，發現嘗試加入第 \(i\) 個點時形成的交錯樹 \(T\) 等於當前相等子圖形成的交錯樹 \(T'\)。因原二分圖存在完美匹配，故 \(T\) 存在增廣路，故 \(T'\) 存在增廣路，故必然存在某次加邊使得出現從 \(i\) 出發的增廣路。

當 \(i = 1\) 時，命題顯然成立，故原命題成立，KM 演演算法正確性得證。

3.3.2 實現方法

根據理論分析，容易得到一個樸素實現 KM 的演演算法。

設當前希望加入節點 \(i\)，則不斷從 \(i\) 開始搜尋。每次開始搜尋前清空右部點的存取標記，以及右部點的 \(slack_y\) 表示 \(\min A_x + B_y - w_{x, y}\) 初始化為 \(+\infty\)，其中 \(x\) 為交錯樹上的左部點。

類似匈牙利演演算法，設當前搜尋到左部點 \(x\)，

• 遍歷 \(x\) 所有出邊對應的右部點 \(y\in N(x)\)：
  • 若 \(y\) 已被存取，則跳過。
  • 否則，若 \(A_x + B_y = w_{x, y}\)，則 \((x, y)\) 在相等子圖上。回憶匈牙利演演算法，當 \(y\) 為非匹配點或搜尋 \(y\) 匹配的左部點 \(x'\) 成功增廣時，令 \(y\) 匹配 \(x\)，並返回增廣成功的資訊。否則跳過這條邊。
  • 否則 \((x, y)\) 不在相等子圖上，用 \(A_x + B_y - w_{x, y}\) 更新 \(slack_y\)。
• 若此時仍未返回，說明 \(x\) 的所有出邊均無法增廣或不在相等子圖上，返回增廣失敗的資訊。

無需記錄 \(x\) 是否被存取的原因在匈牙利部分已經提到：每個左部點 \(x\) 最多隻會被其匹配的右部點 \(y\) 存取到。

搜尋完畢後，若未能成功增廣，則令 \(d\) 為所有 未被存取 的右部點 \(y\) 的 \(\min\limits_{y} slack_y\)。令所有 被存取 的左部點的頂標減少 \(d\)，被存取 的右部點的頂標增加 \(d\)。否則成功增廣，退出從 \(i\) 開始搜尋的過程。據分析，必然存在某一次搜尋使得可以增廣。

• 所有被存取的左部點即 \(i\) 與所有被存取的右部點的左部匹配點。

因每次搜尋的時間複雜度均為 \(\mathcal{O}(m)\)，而每次搜尋必然往相等子圖中加入至少一條邊，故總複雜度 \(\mathcal{O}(m ^ 2)\)，通常視複雜度為 \(\mathcal{O}(n ^ 4)\)，足以應付大部分題目。

模板題 P6577 程式碼如下。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 500 + 5;
ll e[N][N], A[N], B[N], slack[N];
int n, m, mch[N], vis[N];
bool dfs(int id) {
  for(int it = 1; it <= n; it++) {
    if(vis[it]) continue;
    if(A[id] + B[it] == e[id][it]) {
      vis[it] = 1;
      if(!mch[it] || dfs(mch[it])) return mch[it] = id, 1;
    }
    else slack[it] = min(slack[it], A[id] + B[it] - e[id][it]);
  }
  return 0;
}
int main() {
  cin >> n >> m;
  memset(e, 0xcf, sizeof(e));
  for(int i = 1; i <= m; i++) {
    int y, c, h;
    cin >> y >> c >> h;
    e[y][c] = h;
  }
  memset(A, 0xcf, sizeof(A));
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= n; j++)
      A[i] = max(A[i], e[i][j]);
  for(int i = 1; i <= n; i++) {
    while(1) {
      memset(vis, 0, sizeof(vis));
      memset(slack, 0x3f, sizeof(slack));
      if(dfs(i)) break;
      ll d = 1e18;
      for(int j = 1; j <= n; j++) if(!vis[j]) d = min(d, slack[j]);
      for(int j = 1; j <= n; j++) if(vis[j]) B[j] += d, A[mch[j]] -= d;
      A[i] -= d;
    }
  }
  ll ans = 0;
  for(int i = 1; i <= n; i++) ans += A[i] + B[i];
  cout << ans << "\n";
  for(int i = 1; i <= n; i++) cout << mch[i] << " ";
  cout << "\n";
  return 0;
}

我們發現調整頂標後重新搜尋浪費時間，因為原交錯樹仍然存在，同時往相等子圖中新加入一些邊，這些邊由於其左部點屬於交錯樹，右部點不屬於交錯樹的性質，也會加入交錯樹。為了不浪費已有資訊，考慮 bfs。

設當前希望加入節點 \(i\)，當前 bfs 到的節點為 \(x\)，\(x\) 的初始值為 \(i\)。在開始 bfs 前，清空右部點的存取標記，初始化 \(slack_y\) 為 \(+\infty\)。

• 列舉 \(x\) 的所有出邊 \(y\in N(x)\)：
  • 若 \(y\) 已被存取，則跳過。
  • 否則，用 \(A_x + B_y - w_{x, y}\) 更新 \(slack_y\)。
• 令 \(d\) 為所有未被存取的右部點 \(y\) 的 \(\min slack_y\)，\(y'\) 為取到該最小值的 \(y\)。
• 將所有被存取的左部點的頂標減少 \(d\)，被存取的右部點的頂標增加 \(d\)，未被存取的右部點的 \(slack\) 減少 \(d\)：對於不與任何被存取左部點相連的右部點 \(y\)，其 \(slack\) 為初始值 \(+\infty\)，即使減去 \(d\) 也不會影響到 \(\min slack_y\)。
• 此時 \(slack_{y'} = 0\)，說明 \(y'\) 在相等子圖的交錯樹上。
  • 若 \(y'\) 未被匹配，則找到增廣路，退出 bfs。
  • 否則，令 \(x\) 為 \(y'\) 匹配的左部點，繼續 bfs。

考慮記錄額外資訊從而更新增廣路上所有節點的狀態。仔細思考後發現可以記錄每個右部點 \(y'\) 由哪個右部點 \(y\) 匹配的左部點 \(x\) 擴充套件而來，設為 \(pre_{y'} = y\)，不妨設初始時 \(i\) 匹配右部點 \(0\)。

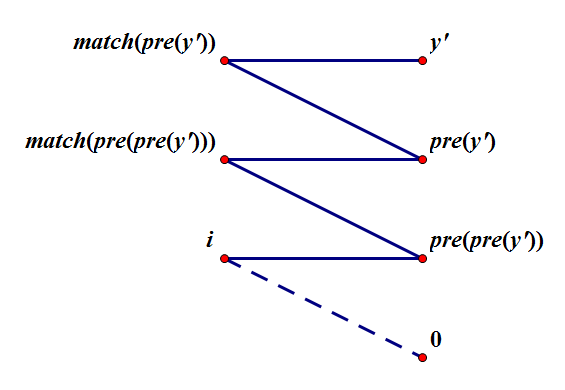
由上圖可知，從退出 bfs 對應的 \(y'\) 開始，此時 \(match(y') = 0\)，不斷令 \(match(y') \gets match(pre(y'))\)，\(y'\gets pre(y')\) 直到 \(y' = 0\) 即可。

如何維護 \(pre\)：根據 dfs 過程，欲知 \(pre(y)\)，只需知道使得 \(slack_y\) 變為 "bfs \(x\) 時對應的 \(d\)" 時對應的左部點 \(x'\)。注意 \(x'\) 不一定等於 \(x\)，因為 \(slack_y\) 可能在 bfs 到 \(x\) 之前就已變為 bfs \(x\) 時對應的 \(d\)，而 \((x, y)\) 不一定滿足 \(A_x + B_y - w_{x, y} = slack_y\)，只是 bfs \(x'\) 時存在比 \(slack_y\) 更小的 \(slack_{y'}\) 使得 \(y\) 在 bfs \(x'\) 時沒有作為取到 \(slack_y\) 最小值的 \(y'\) 而被遍歷到。

因使得 \(slack_y\) 變為某次 bfs 對應的 \(d\) 對應的更新 \((x, y)\) 必然最後一次使 \(slack_y\) 減小，故只需在 bfs \(x\) 時，若 \(A_x + B_y - w_{x, y} < slack_y\)，則用 \(x\) 匹配的右部點 \(y'\)，即使得 bfs 到 \(x\) 的交錯樹右部點，更新 \(pre(y)\)。

若 \(d > 0\)，則 \(\mathcal{O}(n)\) 更新頂標和 \(slack_y\) 後必然加入一條邊，但單次 bfs 的複雜度為 \(\mathcal{O}(n ^ 2)\)（遍歷到的總點數乘以 bfs 單點的複雜度 \(\mathcal{O}(n)\)，後者是卡滿的，因為需要求 \(d\)），故基於 bfs 實現的 KM 演演算法時間複雜度為 \(\mathcal{O}(n ^ 3)\)，可以通過模板題。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 500 + 5;
ll e[N][N], A[N], B[N], slack[N];
int n, m, mch[N], pre[N], vis[N];
void bfs(int id) {
  memset(vis, 0, sizeof(vis));
  memset(slack, 0x3f, sizeof(slack));
  int x = mch[0] = id, y = 0;
  while(1) {
    vis[y] = 1;
    ll d = 1e18;
    int _y = 0;
    for(int i = 1; i <= n; i++) {
      if(vis[i]) continue;
      ll D = A[x] + B[i] - e[x][i];
      if(D < slack[i]) slack[i] = D, pre[i] = y;
      if(slack[i] < d) d = slack[i], _y = i;
    }
    A[id] -= d;
    for(int i = 1; i <= n; i++) {
      if(vis[i]) B[i] += d, A[mch[i]] -= d;
      else slack[i] -= d;
    }
    if(!mch[y = _y]) break;
    x = mch[y];
  }
  while(y) mch[y] = mch[pre[y]], y = pre[y];
}
int main() {
  cin >> n >> m;
  memset(e, 0xcf, sizeof(e));
  for(int i = 1; i <= m; i++) {
    int y, c, h;
    cin >> y >> c >> h;
    e[y][c] = h;
  }
  memset(A, 0xcf, sizeof(A));
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= n; j++)
      A[i] = max(A[i], e[i][j]);
  for(int i = 1; i <= n; i++) bfs(i);
  ll ans = 0;
  for(int i = 1; i <= n; i++) ans += A[i] + B[i];
  cout << ans << "\n";
  for(int i = 1; i <= n; i++) cout << mch[i] << " ";
  cout << "\n";
  return 0;
}

3.4 一般圖最大匹配

NOI 後再更。

3.5 一般圖最大權匹配

NOI 後再更。

4. 參考文章

第一章：

• 網路流與二分圖 學習筆記 - ycx。
• 最大流 - OI Wiki。

第二章：

• Dinic 二分圖匹配 / Hopcroft-Karp 演演算法 複雜度簡單證明 - Itst。
• Konig 定理及證明 - Bennettz。

第三章：

• 圖匹配 - OI Wiki。
• 題解 P6577 - ix35。
• KM 演演算法原理 + 證明 - 夢之淚殤。