首先，標準化的英文是Standardization，歸一化的英文是Normalization，正則化的英文是Regularization。標準化是特徵縮放的一種方式，需要注意的是標準化之後的資料分佈並不一定是正態分佈，因為標準化並不會改變原始資料的分佈。歸一化的目的是消除不同量綱及單位影響，提高資料間的可比性。正則化的目的是為了防止過擬合。文中涉及程式碼下載參考[5]。

一.標準化

1.標準化方程

最常用的標準化就是Z-Score標準化，簡單理解就是減均值，併除以標準差。用方程表示如下：

其中，\(\mu\)是樣本均值，\(\sigma\)是樣本標準差。

2.標準化視覺化

標準化的過程分為2個步驟，第1步是減均值，第2步是除以標準差。視覺化分析如下：

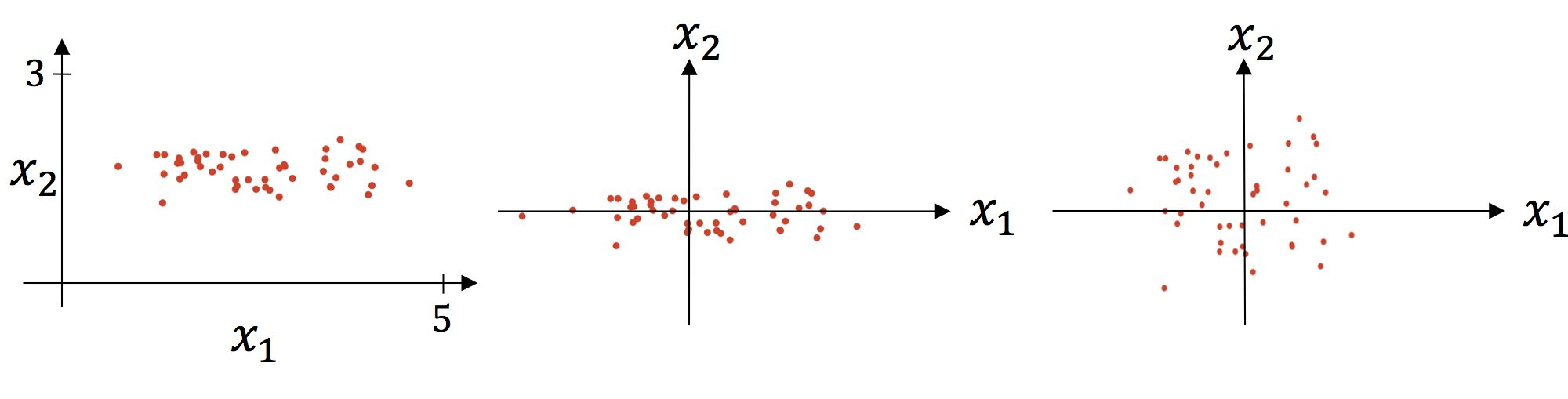
上圖中左圖是原圖視覺化，中圖是減均值後的視覺化，右圖是除以標準差後的視覺化。

3.標準化實現

from sklearn import preprocessing
import numpy as np

X_train = np.array([[1., -1., 2.], [2., 0., 0.], [0., 1., -1.]])
X_train_result = preprocessing.scale(X_train, axis=0) #axis=0表示按列進行標準化
print(X_train_result)
print(X_train_result.mean(axis=0)) #均值為0
print(X_train_result.std(axis=0))  #標準差為1

輸出結果如下：

[[ 0.         -1.22474487  1.33630621]
 [ 1.22474487  0.         -0.26726124]
 [-1.22474487  1.22474487 -1.06904497]]
[0. 0. 0.]
[1. 1. 1.]

如果在做機器學習模型訓練的時候，想把訓練集的縮放標準應用到測試集上，那就要使用StandardScaler()這個類了。程式碼如下：

from sklearn import preprocessing
import numpy as np

X_train = np.array([[1., -1., 2.], [2., 0., 0.], [0., 1., -1.]])
scaler = preprocessing.StandardScaler().fit(X_train)
X_scaled = scaler.transform(X_train)
print(X_scaled.mean(axis=0)) #均值為0
print(X_scaled.std(axis=0))  #標準差為1
X_test = [[-1., 1., 0.]]     #使用訓練集的縮放標準來標準化測試集，這裡的縮放標準指的就是訓練集的列的均值和標準差
print(scaler.transform(X_test))

輸出結果如下：

[0. 0. 0.]
[1. 1. 1.]
[[-2.44948974  1.22474487 -0.26726124]]

二.歸一化

歸一化就是把資料壓縮到一個區間內，比如[0,1]、[-1,1]。常用的2種方法如下：

1.Min-Max Normalization

用方程表示如下：

歸一化的區間範圍是[0,1]。程式碼實現如下：

import numpy as np
from sklearn import preprocessing as pp
X_train = np.array([[ 1., -5., 8.], [ 2., -3., 0.], [ 0., -1., 1.]])
scaler = pp.MinMaxScaler().fit(X_train) #預設資料壓縮範圍為[0,1]
print(scaler.transform(X_train))

輸出結果如下：

[[0.5   0.    1.   ]
 [1.    0.5   0.   ]
 [0.    1.    0.125]]

2.Mean Normalization

用方程表示如下：

歸一化的區間範圍是[-1,1]。

import numpy as np
from sklearn import preprocessing as pp
X_train = np.array([[ 1., -5., 8.], [ 2., -3., 0.], [ 0., -1., 1.]])
scaler = pp.MinMaxScaler(feature_range=(-1, 1)) #設定資料壓縮範圍為[-1,1]
scaler = scaler.fit(X_train)
print(scaler.transform(X_train))

輸出結果如下：

[[ 0.   -1.    1.  ]
 [ 1.    0.   -1.  ]
 [-1.    1.   -0.75]]

上述程式碼主要使用scikit-learn的預處理子模組preprocessing提供MinMaxScaler類來實現歸一化功能。MinMaxScaler類有一個重要引數feature_range，該引數用於設定資料壓縮的範圍，預設值是[0,1]。

三.正則化

  簡單理解使用正則化的目的就是為了防止過擬合，當然還有其它防止過擬合的方法，比如降低特徵維度。先舉個例子說下為什麼降低特徵維度也可以防止過擬合，然後再說明正則化是如何防止過擬合的。首先要搞明白過擬合的本質是什麼？就是把噪音也當做事物的特徵進行了建模。假如一隻小鳥受傷了，暫時不會飛翔，在構建鳥類分類器的時候，把能否飛翔這個噪音也學習成模型的特徵了，這樣正常的能夠飛翔的小鳥就判斷為不是鳥類了，當然這是一個過擬合的很牽強的例子，但是也可說明一定的問題。正則化是如何防止過擬合的呢？
對於給定的資料集\(D = \left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right), \cdots ,\left( {{x_m},{y_m}} \right)} \right\}\)，考慮最簡單的線性迴歸模型，以平方誤差作為損失函數，優化目標如下：

引入L2範數正則化，稱為嶺迴歸[ridge regression]，如下所示：

引入L1範數正則化，稱為LASSO[Least Absolute Shrinkage and Selection Operator]迴歸，如下所示：

假設資料維度為2維，通過方程\(\sum\limits_{j = 1}^M {{{\left| {{w_j}} \right|}^q}} \le \frac{1}{\lambda }\)(這裡沒有展開推導，若感興趣可參考[3])可以做出下圖，其中左圖即\(w_1^2 + w_2^2 \le \frac{1}{\lambda }\)，右圖即\(\left| {{w_1}} \right| + \left| {{w_2}} \right| \le \frac{1}{\lambda }\)。可見隨著\({\lambda }\)增大，越來越多的引數會變為0：

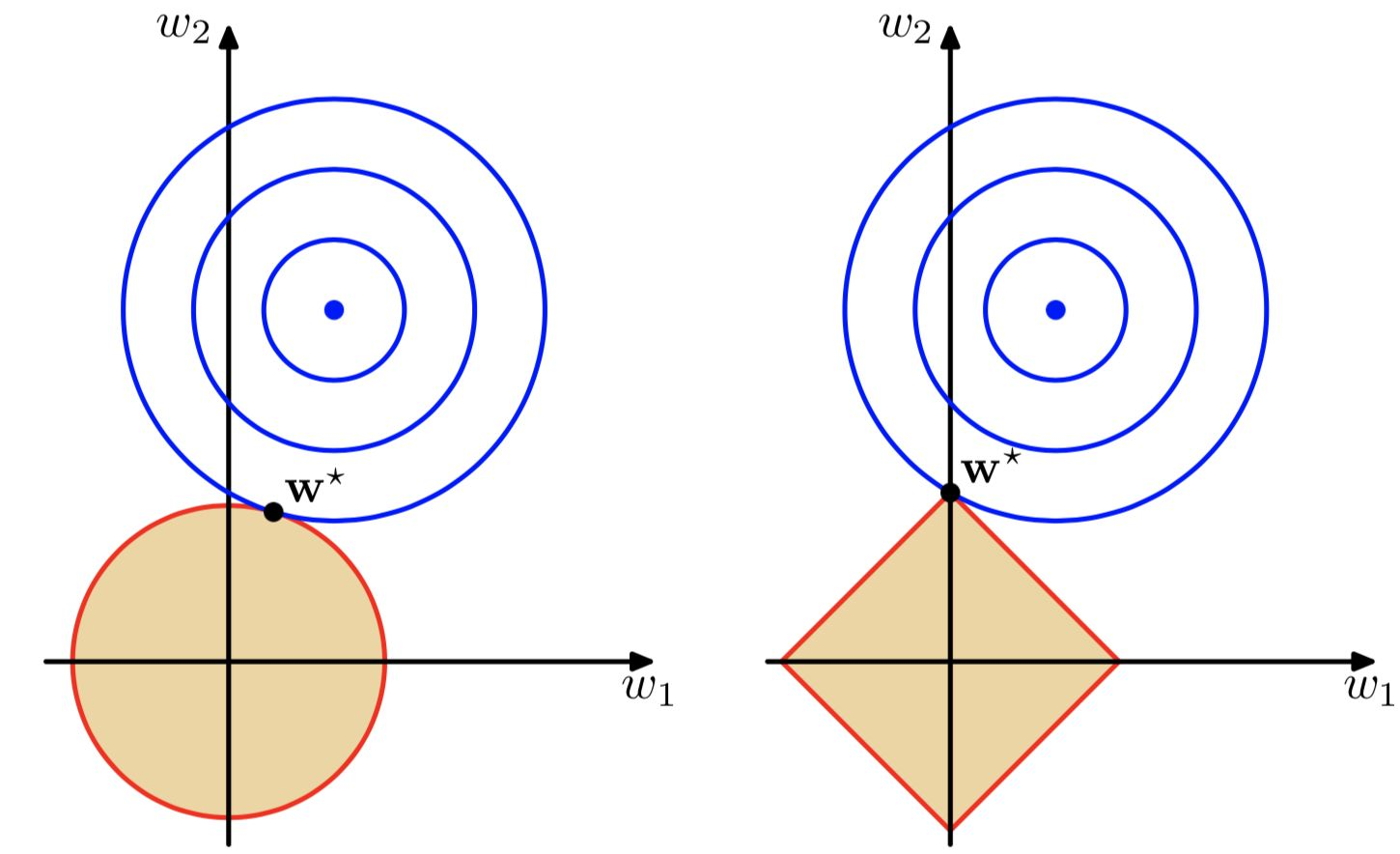
  目的是為了找到損失函數取最小值時對應的權重值，其中下圖藍色圓圈是平方誤差項等值線，當取橢圓中心點時，損失函數(這裡說的損失函數不包含正則化)值最小。總的損失函數(這裡說的損失函數包含正則化)就是求藍圈+紅圈的和的最小值。
  正則化方法是一個常數，它通過限制模型的複雜度，使得複雜的模型能夠在有限大小的資料集上進行訓練，而不會產生嚴重的過擬合。正則項越小，懲罰力度越小，極端情況正則項為0時，就會造成過擬合問題；正則化越大，懲罰力度越大，就會容易出現欠擬合問題。

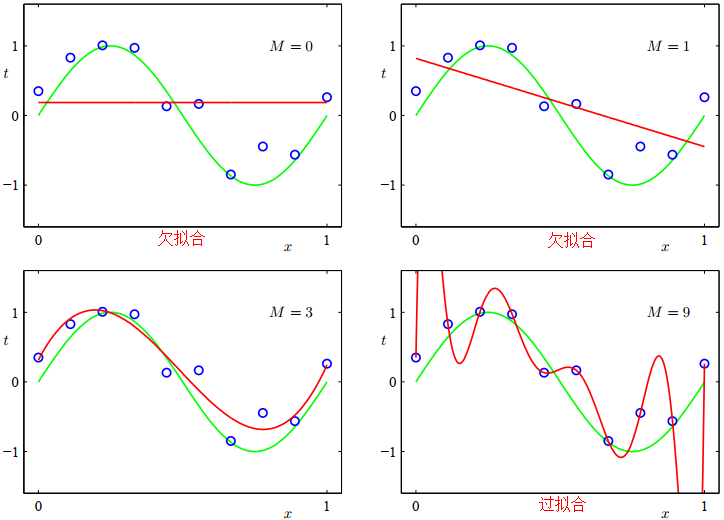
  通過上圖可以直觀的看到採用L1範數時平方誤差項等值線與正則化項等值線的交點出現在座標軸上，即\({w_1} = 0\)或者\({w_2} = 0\)。當採用L2範數時，兩者的交叉點常出現在某個象限中，即\({w_1} \ne 0\)且\({w_2} \ne 0\)。這樣採用L1正則化比L2正則化更容易得到稀疏解。L2正則化優勢是處處可導，L1正則化有拐點，不是處處可微，但可以得到更加稀疏的解。

參考文獻：
[1]Preprocessing data：https://scikit-learn.org/stable/modules/preprocessing.html
[2]機器學習中常常提到的正則化到底是什麼意思：https://www.zhihu.com/question/20924039
[3]圖形識別和機器學習[中文版]：https://url39.ctfile.com/f/2501739-616549609-5fe8d7?p=2096 (存取密碼: 2096)
[4]圖形識別與機器學習[英文版]：https://url39.ctfile.com/f/2501739-616549614-9897ab?p=2096 (存取密碼: 2096)
[5]標準化、歸一化和正則化的關係.py：https://url39.ctfile.com/f/2501739-616549789-16fc6a?p=2096 (存取密碼: 2096)