技術文章 » 強化學習-學習筆記15 | 連續控制

強化學習-學習筆記15 | 連續控制

2022-07-15 06:01:33

本系列的完結篇，介紹了連續控制情境下的強化學習方法，確定策略 DPG 和隨機策略 AC 演演算法。

15. 連續控制

15.1 動作空間

  • 離散動作空間

    • \(Action \ space \ \mathcal{A}={left,right,up}\)
    • 比如超級瑪麗遊戲中的向上\向左\向右；
    • 此前博文討論的，都是離散的控制，動作有限。

  • 連續動作空間

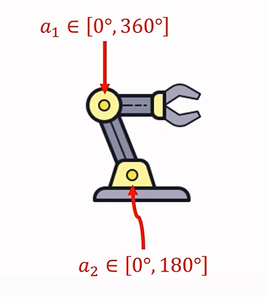
    • \(Action \ space \ \mathcal{A}=[0°,360°]×[0°,180°]\)

    • 比如機械臂，如果具有兩個運動關節：

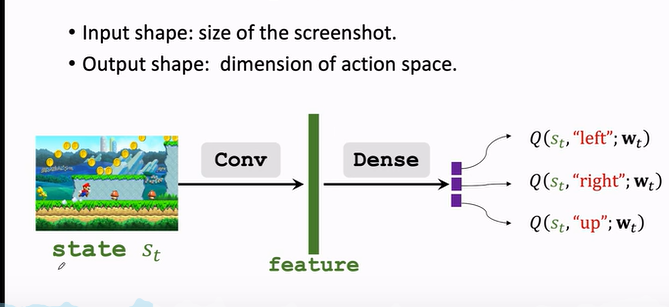
  • 價值網路 DQN 可以解決離散動作控制的問題，因為 DQN 輸出的是有限維度的向量。

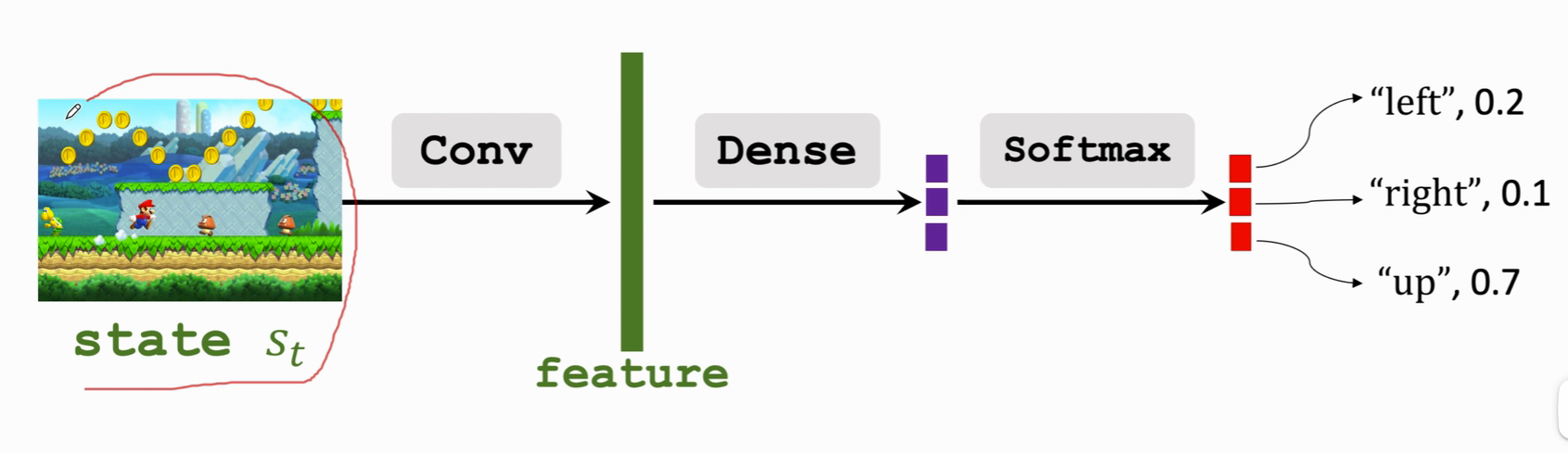
  • 策略網路也同樣。

  • 所以此前的方法不能簡單照搬到連續控制。要想應用到連續控制上，可以採用 連續空間離散化。

連續空間離散化：

  • 比如機械臂進行二維網格劃分。那麼有多少個格子，就有多少種動作。
  • 缺點：假設d為連續動作空間的自由度，動作離散化後的數量會隨著d的增加呈現指數增長，從而造成維度災難。動作太多會學不好DQN 或 策略網路。
  • 所以 離散化 適合自由度較小的問題。

另外還有兩個方法：

  1. 使用確定策略網路(\(Deterministic \ policy \ network\))
  2. 使用隨機策略(\(Stochastic \ policy \ network\))。

15.2 DPG | 確定策略

a. 基礎瞭解

Deterministic Policy Gradient.確定策略梯度，可以用於解決連續控制問題。後續引入深度神經網路，就是著名的 DDPG。

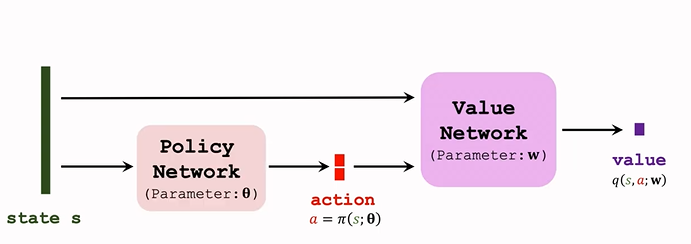
DPG 是 Actor-Critic 方法的一種。結構圖如下：

  • 策略網路 actor

    • 策略網路是確定性的函數 \(a=\pi(s;\theta)\)
    • 輸入是狀態 s ；輸出是一個具體的動作 s；即給定狀態輸出具體的動作，無隨機性。
    • 輸出的動作是可以指導運動的實數或向量。

  • 價值網路 critic

    • 記作 \(q(s,a;w)\)
    • 輸入是狀態 s 和 動作 a，基於狀態 s，評價動作 a 的好壞程度，輸出一個分數 q；

  • 訓練兩個神經網路，讓兩個網路越來越好。

  • 用 TD 演演算法更新 價值網路：

    1. 觀測 transition:\((s_t,a_t,r_t,s_{t+1})\)

    2. 價值網路預測 t 時刻 的動作價值 \(q_t=q(s_t,a_t;w)\)

    3. 價值網路預測 t+1時刻的價值：\(q_{t+1}=q(s_{t+1},a'_{t+1};w)\)

      注意這裡的 \(a'_{t+1}\) 是 策略網路 t+1 時刻預選出來的動作，尚未執行。

    4. TD error：\(\delta_t=q_t-\underbrace{(r_t+\gamma\cdot q_{t+1})}_{TD \ target}\)

    5. 更新引數：\(w\leftarrow w-\alpha\cdot\delta_t \cdot \frac{\partial q(s_t,a_t;w)}{\partial w}\)

  • 策略網路用 DPG 演演算法 更新

b. 演演算法推導

對 DPG 演演算法進行推導。

  • 訓練價值網路的目標是，讓價值網路的輸出 q 越大越好。

  • 而在DPG 的網路結構中，在給定狀態時，動作是確定的（策略網路會給出一個確定的動作），且價值網路固定，那麼影響輸出的就是策略網路的引數 \(\theta\)。

  • 所以更新 θ 使價值 q 更大；

  • 計算價值網路關於 θ 的梯度 DPG：\(g=\frac{\partial q(s,\pi(s;\theta))}{\partial\theta}=\frac{\partial a}{\partial\theta}\cdot\frac{\partial q(s,a;w)}{\partial a}\)

    鏈式法則，讓梯度從價值 q 傳播到動作 a；再從 a 傳播到策略網路。

  • 梯度上升更新 \(\theta\)：\(\theta\leftarrow \theta+\beta\cdot g\)

c. 演演算法改進1 | 使用 TN

上面的 DPG 是比較原始的版本，用 Target Network 可以提升效果。Target Network 在此前第11篇中講過，上文中的演演算法也會出現高估問題或者低估問題。

因為用自身下一時刻的估計來更新此時刻的估計。

Target Network 方法的過程是：

  1. 用 價值網路 計算 t 時刻的價值: \(q_t=q(s_t,q_t;w)\)
  2. TD target (不同之處):
    • 改用兩個不同的神經網路計算 TD target 。
    • 用 target policy network 代替 策略網路 來預選 \(a'_{t+1}\)，網路結構和策略網路一樣，但引數不一樣；記為 \(a'_{t+1}=\pi(s_{s+1};\theta^-)\)
    • 用 target value network 代替 價值網路 計算 \(q_{t+1}\)，與價值網路結構相同，引數不同；記為 \(q_{t+1}=q(s_{t+1},a'_{t+1};w^-)\)
  3. 後續 TD error 以及 引數更新 與 原始演演算法一致，具體見第11篇

d. 完整過程

  1. 策略網路做出選擇:\(a=\pi(s;\theta)\)
  2. 用 DPG 更新 策略網路：\(\theta\leftarrow \theta+ \beta\cdot\frac{\partial a}{\partial\theta}\cdot\frac{\partial q(s,a;w)}{\partial a}\)
  3. 價值網路計算 \(q_t\)：\(q_t=q(s,a;w)\)
  4. Target Networks 計算 \(q_{t+1}\)
  5. TD error：\(\delta_t=q_t-(r_t+\gamma\cdot q_{t+1})\)
  6. 梯度下降：\(w\leftarrow w-\alpha\cdot\delta_t \cdot\frac{\partial q(s,a;w)}{\partial w}\)

同樣，之前講過的其他改進也可以用於這裡，如經驗回放、multi-step TD Target 等。

15.3 確定策略 VS 隨機策略

DPG 使用的是 確定策略網路，跟之前的隨機策略不同。

\ 隨機策略 確定策略
策略函數 $\pi(a s;\theta)$
輸出 每個動作一個概率值，向量 確定的動作
控制方式 根據概率分佈抽樣a 輸出動作並執行
應用 大多是離散控制，用於連續的話結構大有不同 連續控制

15.4 | 隨機策略

這部分來介紹怎麼在連續控制問題中應用隨機策略梯度。

構造一個策略網路，來做連續控制，這個策略網路與之前學過的相差很大，以機械臂為例：

a. 自由度為 1 的連續動作空間

先從一個簡單的情況研究起，自由度為1，這時動作都是實數 \(\mathcal{A}\subset \mathbb{R}\)

  • 記均值為 \(\mu\)，標準差是 \(\sigma\) ，都是狀態 s 的函數，輸出是一個實數
  • 假定我們的策略函數是正態分佈函數\(N(\mu,\sigma^2)\)：\(π(a|s)=\frac{1}{\sqrt{6.28}\sigma}\cdot exp(-\frac{(a-\mu)^2}{2\sigma^2})\)
  • 根據策略函數隨機抽樣一個動作

b. 自由度 >1 的連續動作空間

而機械臂的自由度通常是3或者更高，把自由度記為 d，動作 a 是一個 d 維的向量。

  • 用粗體 \(\boldsymbol{\mu}\) 表示均值，粗體 \(\boldsymbol{\sigma}\) 表示標準差，都是狀態 s 的函數，輸出是都是 d 維向量
  • 用 \(\mu_i\) 和 \(\sigma_i\) 表示 \(\boldsymbol{\mu}(s)\) 和 \(\boldsymbol{\sigma}(s)\) 輸出的第 i 個元素，假設各個維度獨立，則可以表示成 a 中的函數連乘
  • \(π(a|s)=\Pi_{i=1}^d \frac{1}{\sqrt{6.28}\sigma_i}\cdot exp(-\frac{(a_i-\mu_i)^2}{2\sigma_i^2})\)

但是問題是，我們不知道 具體的 \(\mu , \sigma\)，我們用神經網路來近似它們。

c. 函數近似

  • 用神經網路 \(\mu(s;\theta^\mu)\) 近似 \(\mu\)
  • 用神經網路 \(\sigma(s;\theta^\sigma)\)近似 \(\sigma(s)\)，實際上這樣效果並不好，近似方差的對數更好:\(\boldsymbol{\rho_i=ln\sigma_i^2},for \ i=1,...,d.\)
  • 即用神經網路 \(\boldsymbol\rho(s;\boldsymbol{\theta^\rho})\) 近似 \(\boldsymbol\rho\)；

網路結構如下：

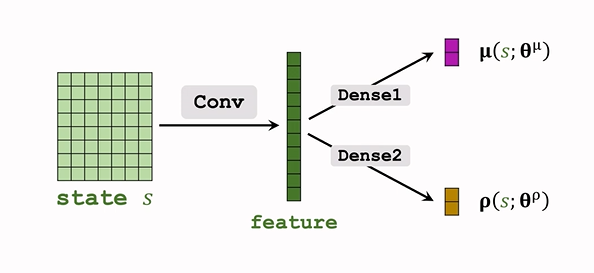
d. 連續控制

  1. 觀測到 狀態 s，輸入神經網路；

  2. 神經網路輸出 \(\hat\mu=\mu(s;\theta^\mu),\hat\rho=\rho(s;\theta^\rho)\)，都是 d 維度

  3. \(\hat\rho\) 計算 \(\hat\sigma_i^2=\exp(\hat\rho_i)\)

  4. 隨機抽樣得到動作 a ：\(a_i\sim\mathcal{N}(\hat\mu_i,\hat\sigma_i^2)\)

    這個正態分佈是假定的策略函數。

e. 訓練策略網路

1. 輔助神經網路

Auxiliary Network, 計算策略梯度時對其求導。

  • 隨機策略梯度為：\(g(a)=\frac{\partial ln\pi(a|s;\theta)}{\partial\theta}\cdot Q_\pi(s,a)\)

  • 計算 \(\pi\) 的對數。

  • 策略網路為：\(\pi(A|s;\theta^\mu)=\Pi_{i=1}^d\frac{1}{\sqrt{6.28}}\cdot\exp(-\frac{(a_i--\mu)^2}{2\delta^2_i})\),輸出是一個概率密度，表示在某點附近的可能性大小

    雖然可以算出來某個動作的概率，但實際上我們只需要知道 均值 和 方差，來做隨機抽樣即可，所以實際上我們用不到這個策略函數 \(\pi\)

  • 由上面策略梯度公式知：我們需要策略 \(\pi\) 的對數，所以訓練時，我們會用到策略 \(\pi\) 的對數，而不是 \(\pi\) 本身：

    \[\ln\pi(a|s;\theta^\mu,\theta^\rho)=\sum_{i=1}^d[-\ln\delta_i-\frac{(a_i-\mu_i)^2}{2\delta^2}]+const \]

  • 由於神經網路輸出的時方差對數\(\rho_i\)，而不是\(\delta^2_i\)，所以做個替換：\(\delta_i^2=\exp\rho_i\)

  • \(\ln\pi(a|s;\theta^\mu,\theta^\rho)=\sum_{i=1}^d[-\ln\delta_i-\frac{(a_i-\mu_i)^2}{2\delta^2}]+const\\=\sum_{i=1}^d[-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\exp(\rho_i)}]+const\)

  • 這樣 神經網路的對數 就表示成了 \(\rho,\mu\) 的形式，記 \(\theta=(\theta^\mu,\theta^\rho)\)

  • 把上式連加的一項記為 \(f(s,a;\theta)\)，這就是輔助神經網路 Auxiliary Network.用於幫助訓練。

    • \(f(a,s;\theta)=\sum_{i=1}^d[-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\exp(\rho_i)}]\)

    • f 的輸入是 s, a ，依賴於 \(\rho,\mu\)，所以引數也是 \(\theta\)

    • 結構如下：

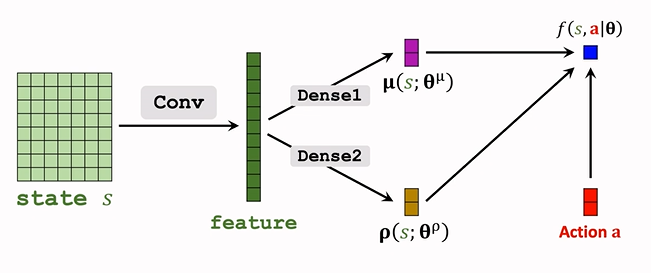
      1. 輸入為 \(\underbrace{\mu,\rho}_{s},a\)，輸出為一個實數 f；

      2. f 依賴於折積層和全連線層的引數，所以接下來反向傳播，可以算出 f 關於全連線層 Dense 引數的梯度，再算出 關於折積層引數的梯度：

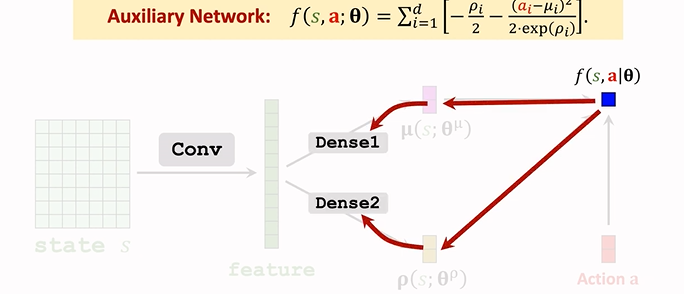
        用 \(\frac{\partial f}{\partial \theta}\) 來表示梯度。

2.策略梯度演演算法訓練策略網路

  • 隨機策略梯度：\(g(a)=\frac{\partial ln\pi(a|s;\theta)}{\partial\theta}\cdot Q_\pi(s,a)\)

  • 輔助神經網路：\(f(s,a;\theta)=\ln\pi(a|s;\theta)+const\)

  • 可以注意到，f 的梯度和 \(\ln\pi\) 的梯度相同，可以用前者梯度代替後者，即

    \[g(a)=\frac{\partial f(s,a;\theta)}{\partial \theta}\cdot Q_\pi(s,a) \]

    而 f 作為一個神經網路，成熟的 pytorch 等可以對其自動求導。

  • Q 還未知，需對其做近似

    • 具體參見 第14篇
    • Reinforce
      • 用觀測到的回報 \(u_t\) 來近似 \(Q_\pi\)
      • 更新策略網路：\(\theta\leftarrow\theta+\beta\cdot\frac{\partial f(s,a;\theta)}{\partial\theta}\cdot u_t\)
    • Actor-Critic（A2C）
      • 用價值網路 \(q(s,a;w)\) 近似 \(Q_\pi\)
      • 更新策略網路：\(\theta\leftarrow\theta+\beta\cdot\frac{\partial f(s,a;\theta)}{\partial\theta}\cdot q(s,a;w)\)
      • 而新引入的價值網路 \(q(S,a;w)\)，用 TD 演演算法來進行學習。

15.5 總結

  1. 連續動作空間有無窮多種動作數量

  2. 解決方案包括：

    • 離散動作空間，使用標準DQN或者策略網路進行學習，但是容易引起維度災難

    • 使用確定策略網路進行學習

      沒有隨機性，某些情境下不合適。

    • 隨機策略網路（\(\mu\) 與 \(\sigma^2\)）

  3. 隨機策略的訓練過程：

    • 構造輔助神經網路 \(f(s,a;\theta)\) 計算策略梯度；
    • 策略梯度近似演演算法包括：reinforce、Actor-Critic 演演算法
      • 可以改進 reinforce 演演算法，使用帶有 baseline 的 reinforce 演演算法
      • 可以改進 Actor-Critic 演演算法，使用 A2C 演演算法

本系列完結撒花！

x. 參考教學