面試官:完全揹包都不會,是你自己走還是我送你?
面試官:完全揹包都不會,是你自己走還是我送你?
在如今的面試當中演演算法題已經成為面試不可或缺的內容,今天就跟大家分享一個還比較困難的筆試題——完全揹包。
完全揹包問題
有\(N\)種物品和一個容量是 \(V\)的揹包,每種物品都有無限件可用。第\(i\) 種物品的體積是 \(v_i\),價值是\(w_i\)。求解將哪些物品裝入揹包,可使這些物品的總體積不超過揹包容量,且總價值最大。
完全揹包問題和01揹包的唯一區別就在於物品的個數,在01揹包當中所有的物品只有一件,也就只能使用一次。而在完全揹包當中物品可以使用無限多次。
比如下面的4個物品,揹包能夠承受的最大重量為5,我們應該如何選擇,使得我們獲得的總價值最大:
| 物品 | 重量 | 價值 |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 4 |
| C | 3 | 4 |
| D | 4 | 5 |
這個問題還是比較簡單,我們直接從圖中看,我們可以選擇五個A或者兩個B一個A,可以產生最大的收益,最大收益為10。
完全揹包問題分析
01揹包動態轉移方程分析
在01揹包問題當中,我們是使用一個二維陣列dp[i][j]進行計算,dp[i][j]表示在只使用前i個物品且揹包容量為j的情況下,我們能夠獲得的最大的收益。在這個情況下,我們根據當前揹包容量j判斷是否能裝入第i個物品可以得到下面兩個方程(下面公式字母的含義與上文完全揹包問題所提到的一致)。
上面01揹包的公式的第二條比較簡單,如果揹包容量不足以容納第i件物品,那麼只能從前i - 1物品當中選擇了。我們來仔細分析一下第一條公式。
如果當前揹包容量可以容納第i個物品,那麼我們就可以選擇第i件物品或者不選擇,我們應該選擇兩種選擇當中收益更大的那個。
- 如果我們不選擇第
i個物品,那麼我們就能夠使用容量為j的揹包去選擇前i - 1個物品,這種情況下我們的最大收益為dp[i - 1][j]。 - 如果選擇第
i個物品,那麼我們揹包容量還剩下j - v[i],還可以選擇剩下的i - 1個物品,而且我們的收益需要加上w[i],因此我們的收益為dp[i - 1][j - v[i]] + w[i], dp[i - 1][j])。
完全揹包動態轉移方程分析
和01揹包問題一樣首先對於第i個物品,首先需要判斷揹包是否能夠容納:
- 如果揹包的容量大於等於第
i個物品的體積,那我們就有兩種選擇:- 將第
i個物品放入揹包當中,但是在這裡需要注意的一點是完全揹包的物品有無數件,因此當我們選擇之後我們的轉移方程為dp[i][j - v[i]] + w[i],這裡不是i-1而是i,因為第i件物品有無數件。 - 不將第
i個物品放入揹包當中,那麼我們就能夠使用容量為j的揹包去選擇前i - 1個物品,這種情況下我們的最大收益為dp[i - 1][j]。
- 將第
- 如果揹包容量小於第
i件物品的體積,我們就不能夠選擇第i件物品了,這種情況下我們的最大收益為dp[i - 1][j]。
基於上面的分析我們可以知道完全揹包問題的動態轉移方程為:
揹包問題程式碼構成設計
根據對動態轉移方程的分析,我們可以知道,我們在計算dp[i][j]這個資料的值的時候,我們首先需要將dp[i][j - v[i]]和dp[i - 1][j])的結果計算出來,因為dp[i][j]依賴這兩個資料。
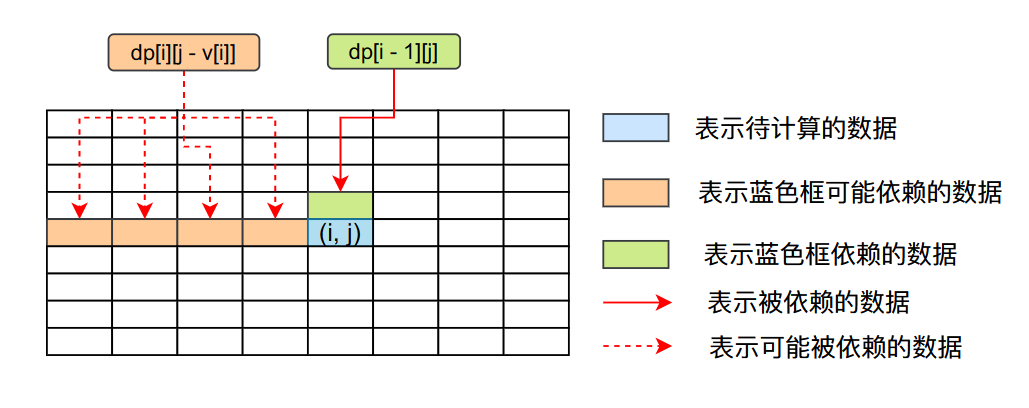
根據上面的分析和圖我們知道,在計算dp[i][j]之前,我們需要將第i行第j列之前的資料和dp[i - 1][j]都計算出來,因為dp[i][j]依賴這些資料。而我們最終需要的結果是dp[N][V]表示在揹包容量為V且能夠前N個物品(也就是所以物品)能夠獲得的最大的收益,所以我們最終需要求出dp[N][V]的值。
因此基於以上分析,我們要想最終解出dp[N][V]的值,我們可以採取兩重for迴圈,第一重回圈遍歷物品,第二重回圈遍歷容量,但是我們的第0行沒有前一行,因此我們需要對第0行進行初始化:
// 對第0行進行初始化操作
for (int i = 0; i <= V; ++i) {
// 如果只能選擇第一個資料,而且能選無數次
// 那就將所有的容量都拿來裝第一個物品
dp[0][i] = i / v[0] * w[0];
}
根據動態轉移方程,我們有下面的程式碼:
for (int i = 1; i < N; ++i) {
for (int j = 0; j <= V; ++j) {
if (j >= v[i]) {
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
C++完整程式碼如下:
#include <iostream>
using namespace std;
#define MAX_LEN 10000
int w[MAX_LEN];
int v[MAX_LEN];
int dp[MAX_LEN][MAX_LEN];
int N, V;
int backpack() {
// 對第0行進行初始化操作
for (int i = 0; i <= V; ++i) {
// 如果只能選擇第一個資料,而且能選無數次
// 那就將所有的容量都哪來裝第一個物品
dp[0][i] = i / v[0] * w[0];
}
for (int i = 1; i < N; ++i) {
for (int j = 0; j <= V; ++j) {
if (j >= v[i]) {
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[N - 1][V];
}
java程式碼如下:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int V = scanner.nextInt();
int[] w = new int[N];
int[] v = new int[N];
int[][] dp = new int[N][V + 1];
for (int i = 0; i < N; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
// 對第0行進行初始化操作
for (int i = 0; i <= V; ++i) {
// 如果只能選擇第一個資料,而且能選無數次
// 那就將所有的容量都哪來裝第一個物品
dp[0][i] = i / v[0] * w[0];
}
for (int i = 1; i < N; ++i) {
for (int j = 0; j <= V; ++j) {
if (j >= v[i]) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
System.out.println(dp[N - 1][V]);
}
完全揹包陣列優化
在前面的內容當中我們已經仔細分析了完全揹包問題的動態轉移方程,我們發現在兩層迴圈的內層迴圈當中,必須從0遍歷到V,因為我們後面的資料依賴同一行前面的資料,還有就是依賴上一行相同列的資料,比如dp[i][j]依賴dp[i][0]到dp[i][j - 1],還依賴dp[i - 1][j],這個其實是可以只用一個陣列進行計算的。
我們先來看單行完全揹包的Java程式碼:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int V = scanner.nextInt();
int[] w = new int[N];
int[] v = new int[N];
int[] dp = new int[V + 1];
for (int i = 0; i < N; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for (int i = 0; i < N; i++) {
for (int j = v[i]; j <= V; j++) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
System.out.println(dp[V]);
}
下面我們舉個使用單行陣列優化的例子:
假如我們正在更新dp[j],此時dp[j]還是第i-1行的狀態而dp[0]到dp[j-1]已經是第i行的狀態了,因為我們是從前到後進行遍歷。而要計算dp[j]的第i行狀態的結果,那麼他需要dp[0]到dp[j-1]的第i行狀態的資料,dp[j]的第i-1行狀態的資料,而實際情況陣列能夠滿足這種依賴關係,因此我們可以使用單行陣列優化。
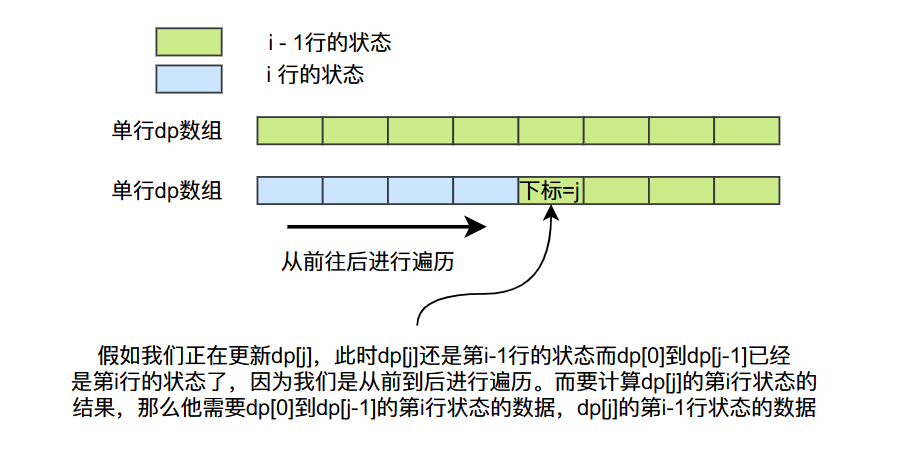
這個單行陣列與多行陣列的區別是多行陣列每一行有每一行的狀態,而且他儲存了所有行的狀態,單行陣列只存在一行的狀態,但是他會經歷所有行的狀態,也就是在外層for迴圈下單行陣列的狀態不斷更新。(如果你不理解這段話和上面談到的單行陣列優化,可以結合程式碼和文字進行理解)
C++程式碼:
#include <iostream>
using namespace std;
#define MAX_LEN 10000
int w[MAX_LEN];
int v[MAX_LEN];
int dp[MAX_LEN]
int N, V;
int backpack() {
for (int i = 0; i < N; ++i) {
for (int j = v[i]; j <= V; ++j) {
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
}
return dp[V];
}
int main() {
cin >> N >> V;
for (int i = 0; i < N; ++i) {
cin >> v[i] >> w[i];
}
cout << backpack();
return 0;
}
總結
在仔細分析完完全揹包問題之後,我們可以總結一下動態規劃的套路:
- 分析問題設定
dp陣列並分析陣列的含義。 - 尋找動態轉移方程,分析
dp陣列當中資料之間的依賴關係,我們在迭代的時候一定要遵循這個關係。 - 初始化陣列。
- 進行陣列
dp求解。 - 分析動態轉移方程的含義和資料依賴關係,分析是否能夠在不破壞資料依賴關係的條件下,優化陣列空間。
其實上面的套路對於大多數動態規劃的題目都有用的,因為動態規劃的流程基本一致,而動態規劃最難的地方就是第一步了,通過分析問題尋找動態轉移方程。
以上就是本篇文章的所有內容了,希望大家有所收穫,我是LeHung,我們下期再見!!!
更多精彩內容合集可存取專案:https://github.com/Chang-LeHung/CSCore
關注公眾號:一無是處的研究僧,瞭解更多計算機(Java、Python、計算機系統基礎、演演算法與資料結構)知識。