wqs二分學習筆記

引入

是什麼？ 能用來解決什麼問題？

序列 \(a\) 有 \(n\) 個元素，求選正好 \(k\) 個元素和的最大值？

這道題可以用排序，但是這道題可以用來理解 wqs 二分 的思路。
用 \(g_k\) 表示選恰好 \(k\) 個元素的最佳答案，把 \((k,g_k)\) 形成的點畫在座標系上，就能得到一個「上凸包」。

例如 \(a = [9,8,4,2,-9,-15]\) 時，

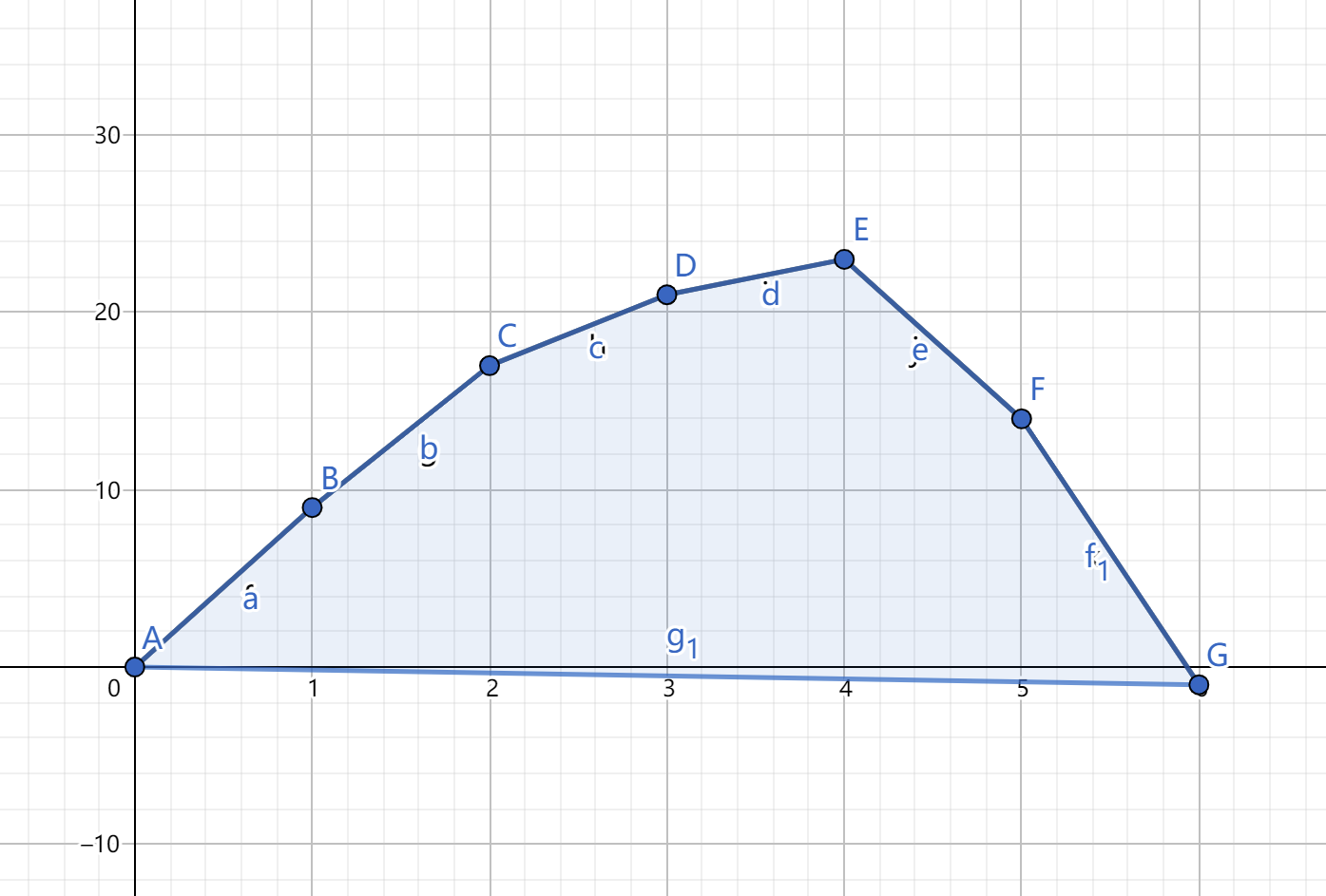
對於大多數題目，如果沒有 \(k\) 的限制（即取的次數的限制），應該是可以在可觀的複雜度內如 \(\mathcal{O}(n)\) 得出答案，比如這道題就是把所有正數加起來，答案相當於求凸包的最高點縱座標。
但是有了準確的次數限制之後就行不通了。

wqs 二分的作用就是能利用這個和 \(k\) 與答案關係 的斜率的單調性，二分一條直線的斜率來切凸包。

什麼是切凸包？

wqs 二分的 check 環節在切凸包。

有了一個確定斜率 \(c\) 的直線之後，假設與凸包切在一個點 \((p,g_p)\)，那麼此時一定滿足直線的「截距」最大，為 \(g_p-c\cdot p\)。

這個可以看作是在每個元素基礎上加上一個代價 \(c\)，就是對於每個元素減 \(c\) 後，計算不帶元素個數限制的本問題的答案 \(\texttt{Maxn}\)，結果就能得到 \((p,g_p)\) 這個點，即 \(\texttt{Maxn} + c\cdot p = g_p\)。

形象地理解，加上代價之後凸包變形，求變形凸包的最高點等同於原來用 \(c\) 斜率的直線切凸包，切出來就是最大的截距。

如下圖所示，\(A'B'C'D'E'F'G'\) 便是上圖變形後的凸包，點 \((i,p_i)\) 由於加上代價，移動到 \((i,p_i-c\cdot i)\)。可以看出，切凸包的斜率為 \(c\) 的線，切到的點就是單次加上代價 \(c\) 後的答案 \(\texttt{Maxn}\)。

動態演示

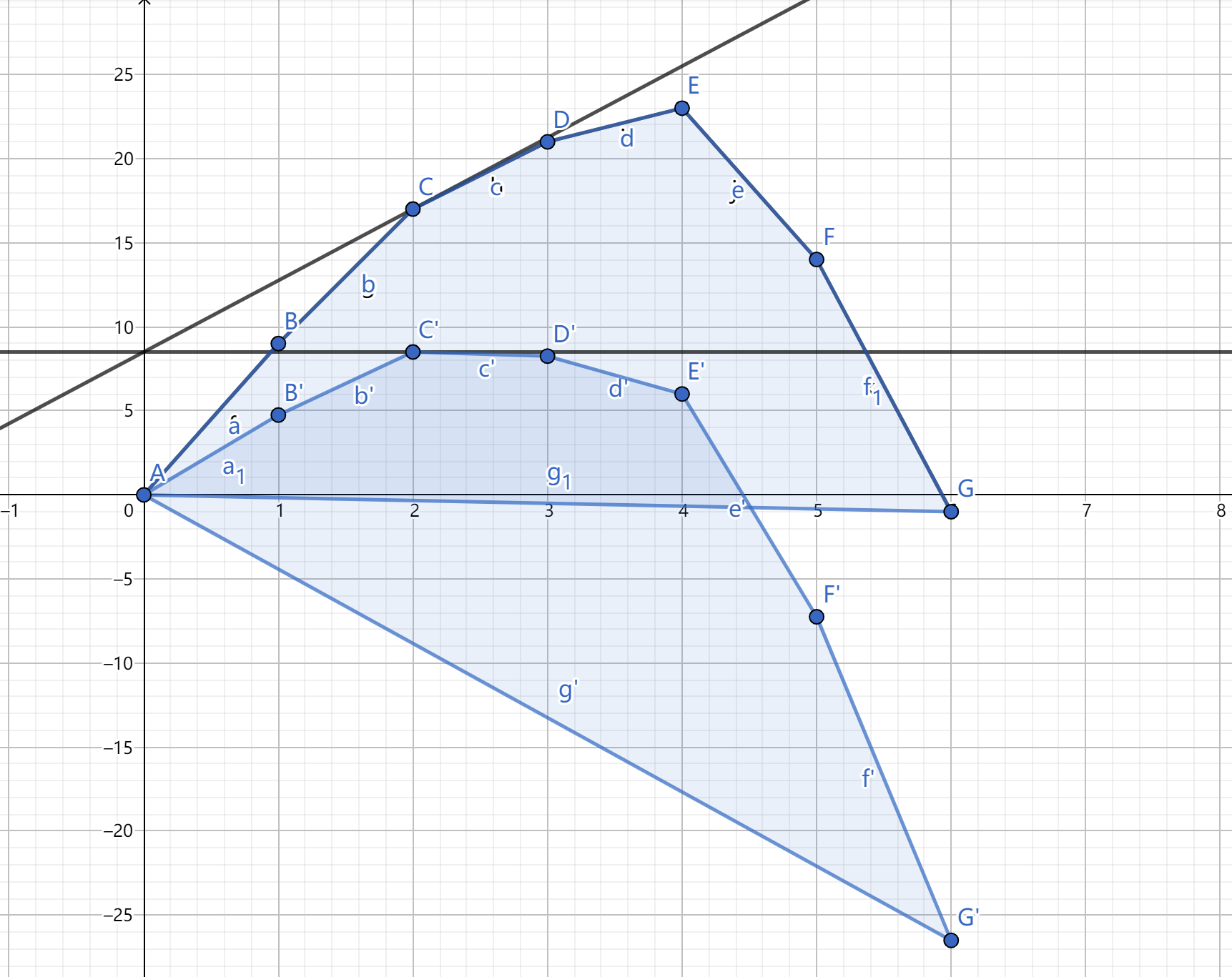
動態演示 By qzhwlzy

高階的動態演示

不斷改變 \(c\)，因為斜率具有單調性，可以看出 \(p\) 是隨著 \(c\) 單調變化的。所以通過不斷二分 \(c\)，可以找到需要的 \(k\) 的限制。

當然這只是一個思想，還有許多細節需要注意。

例題

買賣股票的最佳時機 IV

套用上面的套路可以發現，答案與限制條件之間的關係是滿足 \(k\) 與答案關係 的斜率有單調性，加上代價後的答案可以使用線性的 DP 或貪心計算。

int f[100010][2];
int g[100010][2];

int num, ans;
void fee(int k) { // k 表示每筆交易附加的費用，用於二分
	f[0][1] = -1e9, f[0][0] = 0;
	for (int i = 1; i <= n; i++) {
		if (f[i - 1][0] < f[i - 1][1] + a[i])
			f[i][0] = f[i - 1][1] + a[i], g[i][0] = g[i - 1][1];
		else
			f[i][0] = f[i - 1][0], g[i][0] = g[i - 1][0];
		if (f[i - 1][1] < f[i - 1][0] - a[i] - k) //這樣求出來的交易次數也是最小的
			f[i][1] = f[i - 1][0] - a[i] - k, g[i][1] = g[i - 1][0] + 1;
		else
			f[i][1] = f[i - 1][1], g[i][1] = g[i - 1][1];
	}
	ans = f[n][0];
	num = g[n][0];
}

由於我們知道答案都是整數，斜率只需要二分整數就行了，一定能二分到 \(k\) 的一段。

int main() {
	int i, k;
	int l = 0, r = 1, mid, Ans = -1;
	cin >> n >> k;
	for (i = 1; i <= n; i++)
		cin >> a[i], r = max(r, (int)a[i]);
	while (l <= r) {
		mid = (l + r) / 2;
		fee(mid);
		if (num <= k) {
			Ans = k * mid + ans;
			r = mid - 1;
		} else {
			l = mid + 1;
		}
	}
	if (Ans == -1) {
		fee(0);
		cout << ans << endl;
	} else
		cout << Ans << endl;
	return 0;
}

細節解析：

1. if (Ans == -1) 在此情況下二分失敗，說明 \(k\) 在非正斜率的部分，直接忽略 \(k\) 的限制進行貪心可行；

2. Ans = k * mid + ans; 我們當前切到的點在 \((\texttt{num},\texttt{num} \cdot \texttt{mid} + \texttt{ans})\)，為什麼不寫 Ans = num * mid + ans; 呢？

這就要說一個很噁心的情況了。如果凸包上三點共線，我們只能取到上面的一些特殊點（如最左最右的點），不一定取到 \(k\)；如果讀者想要嘗試，本題目中以下樣例存在該情況：

8 2
3 3 5 0 0 3 1 4

於是，我們用 DP 處理交易次數最大值，在 \(\texttt{num} \ge \texttt{k}\) 時更新答案，只需要最後一次，但因為不一定能取到等號，所以最好都更新。

或者，我們用 DP 處理交易次數最小值，在 \(\texttt{num} \le \texttt{k}\) 時更新答案，只需要最後一次（而且不能使用 \(\max\)），但因為不一定能取到等號，所以最好都更新。

此外在上面的例子中，我們還發現，k * mid + ans 似乎也有一些單調性，(mid,k * mid + ans) 構成的點很像下凸包......不過我們暫時不研究 其實是不會到時候填坑吧

種樹

這道題完美符合上述特點，同樣需要注意三點共線情況。寫法同樣有兩種。
寫法1
寫法2

Tree

與上相同。三份程式碼詳情