強化學習-學習筆記14 | 策略梯度中的 Baseline

本篇筆記記錄學習在 策略學習 中使用 Baseline，這樣可以降低方差，讓收斂更快。

14. 策略學習中的 Baseline

14.1 Baseline 推導

• 在策略學習中，我們使用策略網路 \(\pi(a|s;\theta)\) 控制 agent，

• 狀態價值函數

  \(V_\pi(s)=\mathbb{E}_{A\sim \pi}[Q_\pi(s,A)]=\sum\limits_{a}\pi(a|s;\theta)\cdot Q_\pi(a,s)\)

• 策略梯度：

  \(\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}_{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)]\)

在策略梯度演演算法中引入 Baseline 主要是用於減小方差，從而加速收斂

Baseline 可以是任何 獨立於 動作 A 的數，記為 b。

Baseline的性質：

• 這個期望是0： \(\mathbb{E}_{A\sim\pi}[b\cdot \frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}]=0\)

  • 因為 b 不依賴 動作 A ，而該式是對 A 求期望，所以可以把 b 提出來，有：\(b\cdot \mathbb{E}_{A\sim\pi}[\frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}]\)

  • 而期望 E 這一項可以展開：\(b\sum_a \pi(a|s;\theta)\cdot\frac{\partial\ln_\pi(A|s;\theta)}{\partial\theta}\)

    這個性質在策略梯度演演算法用到的的兩種形式有提到過。

  • 用鏈式法則展開後面的導數項，即: \(\frac{\partial\ln_\pi(A|s;\theta)}{\partial\theta}={\frac{1}{\pi(a|s;\theta)}\cdot \frac{\partial\pi(a|s;\theta)}{\partial\theta}}\)

  • 這樣整個式子為：\(b\sum_a \pi(a|s;\theta)\cdot{\frac{1}{\pi(a|s;\theta)}\cdot \frac{\partial\pi(a|s;\theta)}{\partial\theta}}=b\cdot \sum_a\frac{\partial\pi(a|s;\theta)}{\partial\theta}\)

  • 由於連加是對於 a 進行連加，而內部求導是對於 θ 進行求導，所以求和符號可以和導數符號交換位置：

    \(b\cdot \frac{\partial\sum_a\pi(a|s;\theta)}{\partial\theta}\)

    這是數學分析中 級數部分 的內容。

  • 而 \(\sum_a\pi(a|s;\theta)=1\)，所以有\(b\cdot \frac{\partial 1}{\partial \theta}=0\)

根據上面這個式子的性質，可以向 策略梯度中新增 baseline

• 策略梯度 with baseline：$$\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q\pi(s,A)]- \mathbb{E}{A\sim\pi}[b\cdot \frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}] \=\mathbb{E}{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot(Q_\pi(s,A)-b)]$$
• 這樣引入b對期望 \(\mathbb{E}\) 沒有影響，為什麼要引入 b 呢？
  • 策略梯度演演算法中使用的並不是 嚴格的上述式子，而是它的蒙特卡洛近似；
  • b不影響期望，但是影響蒙特卡洛近似；
  • 如果 b 好，接近 \(Q_\pi\)，那麼會讓蒙特卡洛近似的方差更小，收斂速度更快。

14.2 策略梯度的蒙特卡洛近似

上面我們得到：\(\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}=\mathbb{E}_{A_t\sim\pi}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-b)]\)

但直接求期望往往很困難，通常用蒙特卡洛近似期望。

• 令 \(g(A_t)=[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-b)]\)

• 根據策略函數 \(\pi\) 隨機抽樣 \(a_t\) ，計算 \(g(a_t)\)，這就是上面期望的蒙特卡洛近似；\(g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-b)]\)

• \(g(a_t)\) 是對策略梯度的無偏估計；

  因為：\(\mathbb{E}_{A_t\sim\pi}[g(A_t)]=\frac{\partial V_\pi(s_t)}{\partial\theta}\)，期望相等。

• \(g(a_t)\) 是個隨機梯度，是對策略梯度 \(\mathbb{E}_{A_t\sim\pi}[g(A_t)]\)的蒙特卡洛近似

• 在實際訓練策略網路的時候，用隨機梯度上升更新引數θ：\(\theta \leftarrow \theta+\beta\cdot g(a_t)\)

• 策略梯度是 \(g(a_t)\) 的期望，不論 b 是什麼，只要與 A 無關，就都不會影響 \(g(A_t)\) 的期望。為什麼不影響已經在 14.1 中講過了。

  • 但是 b 會影響 \(g(a_t)\)；
  • 如果 b 選取的很好，很接近 \(Q_\pi\)，那麼隨機策略梯度\(g(a_t)\)的方差就會小；

14.3 Baseline的選取

介紹兩種常用的 baseline。

a. b=0

第一種就是把 baseline 取0，即與之前相同：\(\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}_{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)]\)

b. b= \(V_\pi\)

另一種就是取 b 為 \(V_\pi\)，而 \(V_\pi\) 只依賴於當前狀態 \(s_t\)，所以可以用來作為 b。並且 \(V_\pi\) 很接近 \(Q_\pi\)，可以降低方差加速收斂。

因為 \(V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A_t)]\)，作為期望，V 很接近 Q。

14.4 Reinforce with Baseline

把 baseline 用於 Reinforce 演演算法上。

a. 基本概念

• 折扣回報：\(U_t=R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+...\)

• 動作價值函數：\(Q_\pi(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t].\)

• 狀態價值函數：\(V_\pi(s_t)=\mathbb{E}_A[Q_\pi(s_t,A)|s_t]\)

• 應用 baseline 的策略梯度：使用的是上面第二種 baseline：

  \(\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}=\mathbb{E}_{A_t\sim\pi}[g(A_t)]=\mathbb{E}_{A_t\sim\pi}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-V_\pi(s_t))]\)

• 對動作進行抽樣，用 \(g(a_t)\) 做蒙特卡洛近似，為無偏估計（因為期望==策略梯度）：\(a_t\sim\pi(\cdot|s_t;\theta)\)

  \(g(a_t)\) 就叫做 隨機策略梯度，用隨機抽取的動作 對應的值來代替期望，是策略梯度的隨即近似；這正是蒙特卡洛方法的應用。

  • \(g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-b)]\)

但上述公式中還是有不確定的項:\(Q_\pi \ \ V_\pi\)，繼續近似：

• 用觀測到的 \(u_t\) 近似 \(Q_\pi\)，因為 \(Q_\pi(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t].\)這也是一次蒙特卡洛近似。

  這也是 Reinforce 演演算法的關鍵。

• 用神經網路-價值網路 \(v(s;w)\) 近似 \(V_\pi\)；

所以最終近似出來的 策略梯度 是：

當我們知道 策略網路\(\pi\)、折扣回報\(u_t\) 以及 價值網路\(v\)，就可以計算這個策略梯度。

我們總計做了3次近似：

1. 用一個抽樣動作 \(a_t\) 帶入 \(g(a_t)\) 來近似期望；

2. 用回報 \(u_t\) 近似動作價值函數\(Q_\pi\)；

   1、2都是蒙特卡洛近似；

3. 用神經網路近似狀態價值函數\(V_\pi\)

   函數近似。

b. 演演算法過程

我們需要建立一個策略網路和一個價值網路，後者輔助訓練前者。

• 策略網路：

• 價值網路：

• 引數共用：

用 Reinforce 演演算法訓練策略網路，用迴歸方法訓練價值網路。

• 在一次訓練中 agent 獲得軌跡：\(s_1,a_1,r_1,s_2,a_2,r_2,...\)

• 計算 \(u_t=\sum_{i=t}^n\gamma^{i-t}r^i\)

• 更新策略網路

  1. 得到策略梯度：\(\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(u_t-v(s;w))\)

  2. 梯度上升，更新引數：\(\theta\leftarrow \theta + \beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial\theta}\cdot(u_t-v(s_t;w))\)

     記 \(u_t-v(s_t;w)\) 為 \(-\delta_t\)

     \(\theta\leftarrow \theta - \beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial\theta}\cdot \delta_t\)

• 更新價值網路

  回顧一下價值網路的目標：\(V_\pi\) 是 \(U_t\) 的期望，訓練價值網路是讓v接近期望 \(V_\pi\)

  1. 用觀測到的 \(u_t\) 擬合 v，兩者之間的誤差記為

     prediction error:\(\delta_t=v(s_t;w)-u_t\)，

  2. 求導得策略梯度: \(\frac{\partial \delta^2/2}{\partial w}=\delta_t\cdot \frac{\partial v(s_t;w)}{\partial w}\)

  3. 梯度下降更新引數：\(w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)

• 如果軌跡的長度為n，可以對神經網路進行n次更新

14.5 A2C演演算法

a.基本概念

Advantage Actor Critic. 把 baseline 用於 Actor-Critic 上。

所以需要一個策略網路 actor 和一個價值網路 critic。但與 第四篇筆記AC演演算法有所不同。

• 策略網路還是 \(\pi(a|s;\theta)\)，而價值網路是 \(v(s;w)\)，是對\(V_\pi\) 的近似，而不是第四篇筆記中的 \(Q_\pi\)。

  因為 V 不依賴於動作，而 Q 依賴動作和狀態，故 近似V 的方法可以引入 baseline。

• A2C 網路結構：

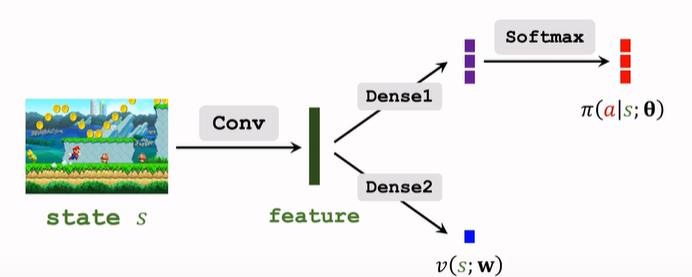
與 14.4 中的結構相同，區別在於訓練方法不同。

b. 訓練過程

1. 觀察到一個 transition(\(s_t，a_t,r_t,s_{t+1}\))

2. 計算 TD target：\(y_t=r_t+\gamma\cdot v(s_{t+1};w)\)

3. 計算 TD error：\(\delta_t=v(s_t;w)-y_t\)

4. 用策略網路梯度更新策略網路θ：\(\theta\leftarrow \theta-\beta\cdot\delta_t\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial \theta}\)

   注意！這裡的 \(\delta_t\)​ 是前文中的 「\(u_t-v(s_t;w)\) 為 \(-\delta_t\)」

5. 用TD更新價值網路：\(w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)

c. 數學推導

A2C的基本過程就在上面，很簡潔，下面進行數學推導。

1.價值函數的性質

• \(Q_\pi\)

  • TD演演算法推導時用到過這個式子：\(Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1},A_{t+1}}[R_t+\gamma\cdot Q_\pi(S_{t+1},A_{t+1})]\)

  • 隨機性來自 \(S_{t+1},A_{t+1}\)，而對之求期望正好消掉了隨機性，可以把對 \(A_{t+1}\) 的期望放入括號內，\(R_t\) 與 \(A_{t+1}\) 無關，則有 定理一：

    \(Q_\pi(s_t,a_t)= \mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot \mathbb{E}_{A_{t+1}}[Q_\pi(S_{t+1},A_{t+1})]\\=\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(s_{t+1})]\)

  • 即：\(Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(s_{t+1})]\)

• \(V_\pi\)

  • 根據定義： \(V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A_t)]\)

  • 將 Q 用 定理一 替換掉：

    \[V_\pi(s_t)=\mathbb{E}_{A_t}\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]\\=\mathbb{E}_{A_t,S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})] \]

  • 這就是 定理二：\(V_\pi(s_t)=\mathbb{E}_{A_t,S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]\)

這樣就將 Q 和 V 表示為期望的形式，A2C會用到這兩個期望，期望不好求，我們是用蒙特卡洛來近似求期望：

• 觀測到 transition(\(s_t,a_t,r_t,s_{t+1}\))

• \(Q_\pi\)

  • \(Q_\pi(s_t,a_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
  • 訓練策略網路；

• \(V_\pi\)

  • \(V_\pi(s_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
  • 訓練價值網路，這也是TD target 的來源；

2. 更新策略網路

即使用 baseline 的策略梯度演演算法。

• \(g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-V_\pi(s_t))]\) 是策略梯度的蒙特卡洛近似。

• 前面Dueling Network提到過，\(Q_\pi-V_\pi\)是優勢函數 Advantage Function.

  這也是 A2C 的名字來源。

• Q 和 V 都還不知道，需要做近似，14.5.c.1 中介紹了：

  • \(Q_\pi(s_t,a_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
  • 所以是：\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot V_\pi(s_{t+1}))-V_\pi(s_t)]\)
  • 對 \(V_\pi\) 進行函數近似 \(v(s;w)\)
  • 則得最終：\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot v(s_{t+1;w}))-v(s_{t;w})]\)

  用上式更新策略網路。

• 而 \(r_t+\gamma\cdot v(s_{t+1;w})\) 正是 TD target \(y_t\)

• 梯度上升更新引數：\(\theta\leftarrow \theta-\beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial \theta}\cdot (y_t-v(s_t;w))\)

  這樣的梯度上升更好。

因為以上式子中都有 V，所以需要近似計算 V：

\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot\underbrace{[(r_t+\gamma\cdot V_\pi(s_{t+1}))-V_\pi(s_t)]}_{evaluation \ made \ by \ the \ critic}\)

3. 更新價值網路

採用 TD 演演算法 更新價值網路，根據 14.5.b 有如下式子：

• \(V_\pi(s_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
• 對上式得 \(V_\pi\) 做函數近似， 替換為 \(v(s_t;w),v(s_{t+1;w})\)；
• \(v(s_t;w)\approx \underbrace{r_t+\gamma\cdot v(s_{t+1};w)}_{TD \ target \ y_t}\)
• 訓練價值網路就是要讓 \(v(s;w)\) 接近 \(y_t\)
  • TD error: \(\delta_t=v(s_t;w)-y_t\)
  • 梯度: \(\frac{\partial\delta^2_t/2}{\partial w}=\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)
  • 更新：\(w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)

4. 有關的策略梯度

在A2C 演演算法中的策略梯度：\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot v(s_{t+1;w}))-v(s_{t;w})]\)

會有這麼一個問題，後面這一項是由價值網路給出對策略網路選出的動作進行打分，那麼為什麼這一項中沒有動作呢，沒有動作怎麼給動作打分呢？

• 注意這兩項：
• \((r_t+\gamma\cdot v(s_{t+1;w}))\) 是執行完 \(a_t\) 後作出的預測
• \(v(s_t;w)\) 是未執行 \(a_t\) 時作出的預測；
• 兩者之差意味著動作 \(a_t\) 對於 V 的影響程度
• 而在AC演演算法中，價值網路給策略網路的是 q，而在A2C演演算法中， 價值網路給策略網路的就是上兩式之差 advantage.

14.6 RwB 與A2C 的對比

• 兩者的神經網路結構完全一樣

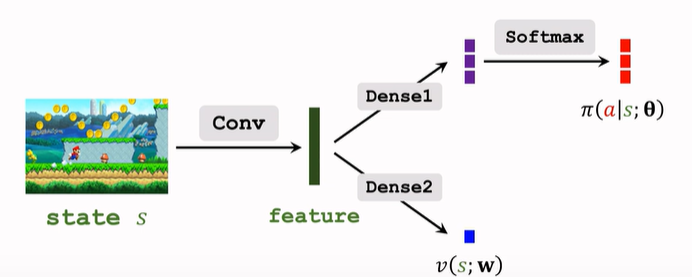
• 不同的是價值網路

  • RwB 的價值網路只作為 baseline，不評價策略網路，用於降低隨機梯度造成的方差；
  • A2C 的價值網路時critic，評價策略網路；

• RwB 是 A2C 的特殊形式。這一點下面 14.7 後會講。

14.7 A2C with m-step

單步 A2C 就是上面所講的內容，具體請見 14.5.b。

而多步A2C就是使用 m 個連續 transition：

• \(y_t=\sum_{i=0}^{m-1}\gamma^i\cdot r_{t+1}+\gamma^m\cdot v(s_{t+m};w)\)
• 具體參見m-step
• 剩下的步驟沒有任何改變，只是 TD target 改變了。

下面解釋 RwB 和 A2C with m-step 的關係：

• A2C with m-step 的TD target：\(y_t=\sum_{i=0}^{m-1}\gamma^i\cdot r_{t+1}+\gamma^m\cdot v(s_{t+m};w)\)
• 如果使用所有的獎勵，上面兩項中的第二項（估計）就不存在，而第一項變成了
  • \(y_t=u_t=\sum_{i=t}^n \gamma^{i-t}\cdot r_i\)
  • 這就是 Reinforce with baseline.

x. 參考教學

• 視訊課程：深度強化學習（全）_嗶哩嗶哩_bilibili
• 視訊原地址：https://www.youtube.com/user/wsszju
• 課件地址：https://github.com/wangshusen/DeepLearning