淺析拉格朗日乘數法及其對偶問題
拉格朗日乘數(Lagrange Multipliers)法
在數學最優問題中,拉格朗日乘數法(以數學家約瑟夫·路易斯·拉格朗日命名)是一種尋找變數受一個或多個條件所限制的多元函數的極值的方法。這種方法將一個有n個變數與k個約束條件的最佳化問題轉換為一個有n + k個變數的方程組的極值問題,其變數不受任何約束。這種方法引入了一種新的標量未知數,即拉格朗日乘數:約束方程的梯度(gradient)的線性組合裡每個向量的係數。此方法的證明牽涉到偏微分,全微分或鏈法,從而找到能讓設出的隱函數的微分為零的未知數的值。
引入問題
給定一個函數:\(z = f(x, y)\)如何求其極值點呢 ?
顯然根據多元函數求極值定理(必要條件):設函數\(z = f(x, y)\)在點\((x_{0}, y_{0})\)具有偏導數,且在點\((x_{0}, y_{0})\)處有極值,則有
\(f_{x}(x_{0}, y_{0})\) = 0, \(f_{y}(x_{0}, y_{0})\) = 0
即:函數在點\((x_{0}, y_{0})\)處有偏導且有極值則該點處偏導為0,具體方法不作敘述,參考高等數學Ⅱ
現在將問題難度加大,如果再加上約束條件呢?面積固定,求體積最大?
正文

上圖是對拉格朗日乘數法的敘述
假設有兩個函數\(f(x,y)\)和\(g(x,y)\),且這兩個函數的一階偏導數都是連續函數,在\(g(x,y)=k\) and \(\triangledown g(a,b)≠(0,0)\)的前提下,函數\(f(x,y)\)在某個\((a,b)\)點產生了區域性極值,可以找到一個實數\(\lambda\)使得\(\triangledown f(a,b)=\lambda \triangledown g(a,b)\)
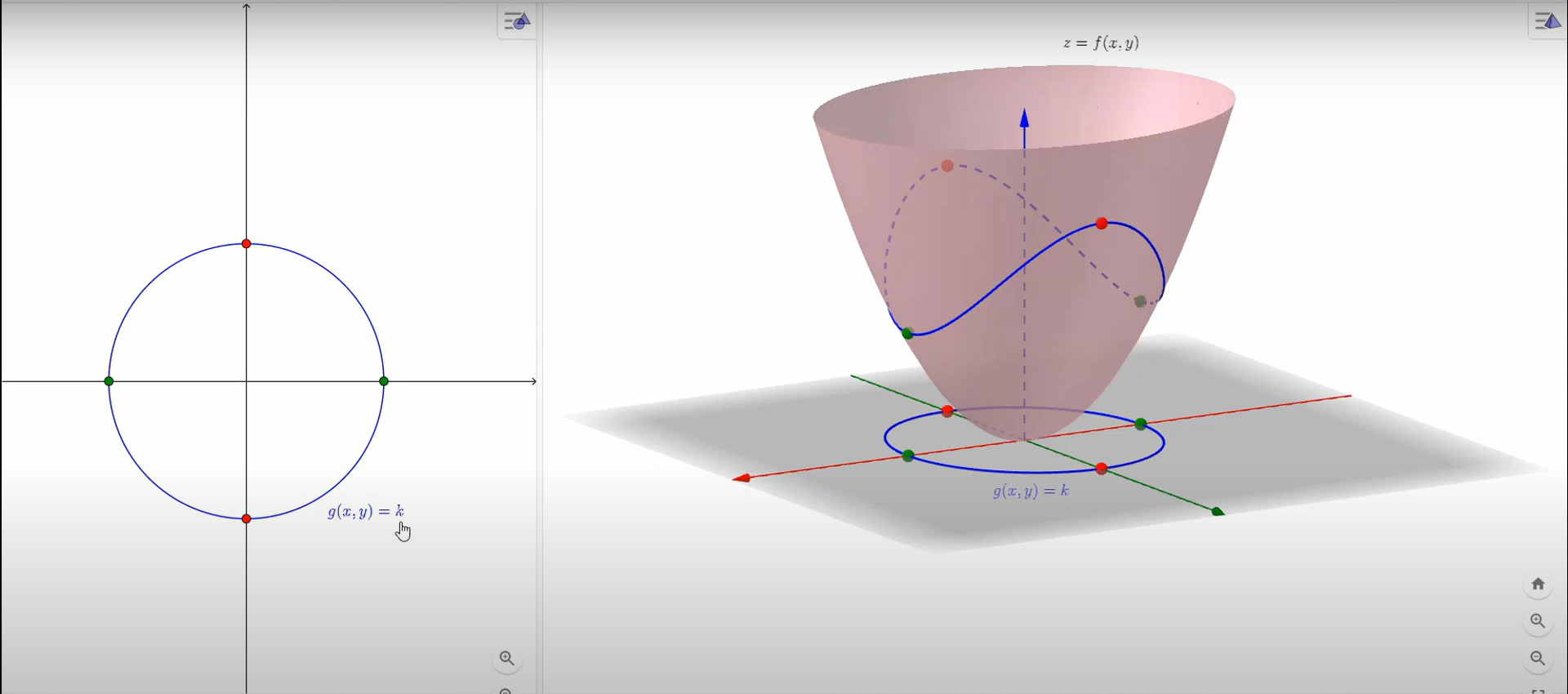
\(f(x,y)\)是右圖中的3D曲面,左圖中的\(g(x,y)\)是約束條件,我們將\(g(x,y)\)向上面的\(f(x,y)\)進行投影可以得到曲面上有一條藍色的曲線,這條曲線就是在\(g(x,y)\)的約束條件下\(f(x,y)\)的所有取值點,接下來我們就要從中找到最值。
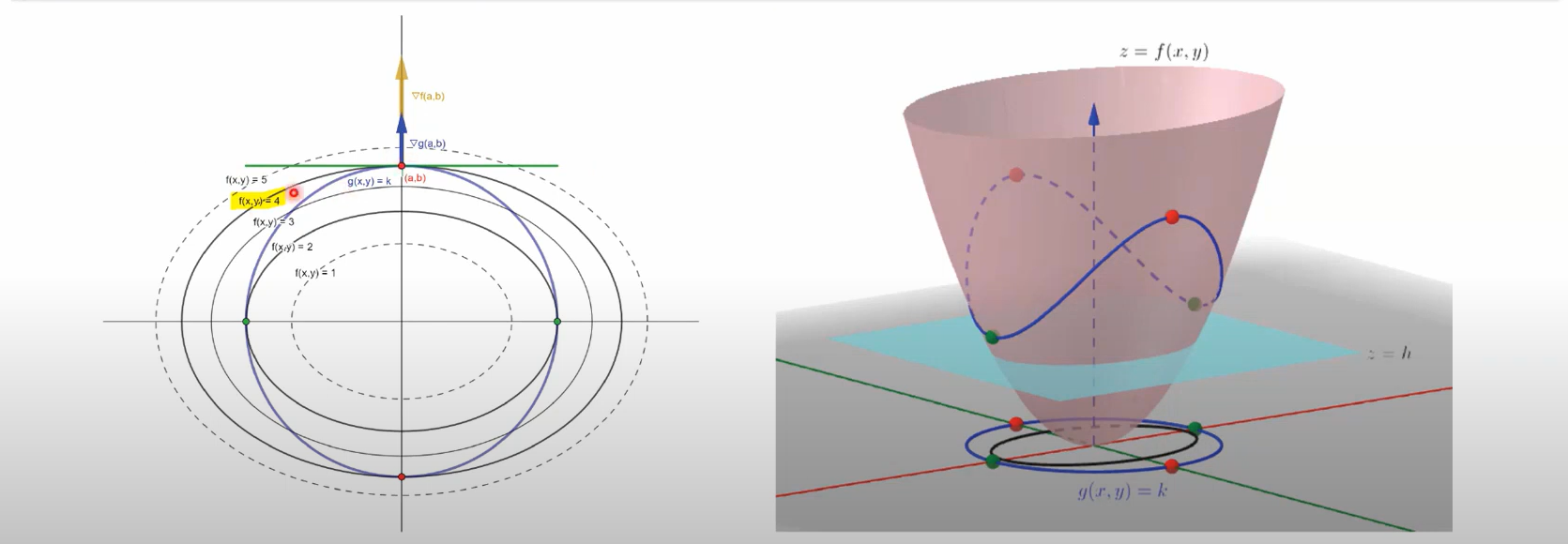
我們引入一個水平面\(z=h\),水平面與曲面相交處的投影是一個橢圓,水平面向上移動時,會首先與曲面上藍色的曲線相交於圖上兩個綠色的點,此時如左圖(投影圖)所示,\(h=2\)。水平面繼續向上移動時會與曲面上藍色的曲線一直相交於4個點,直到相交於兩個點時,即為圖上的紅點,此時如左圖所示,\(h=4\)。當水平面繼續向上移動時就再也不可能與曲面上藍色的曲線相交了。如右圖我們可以知道\(h=2\)和\(h=4\)時的交點是在約束條件下曲面的極值點,並且此時的藍色曲線與水平面相切。在左圖中可以看出當處於極值點時\(f(x,y)\)和\(g(x,y)\)共同相切與同一條直線,所以此時兩函數在此交點的處的法向量是共線的,即\(\triangledown f(x,y)=\lambda \triangledown g(x,y)\)
Ep: Find the extreme values of the function \(f(x,y)=x^{2}+2y^{2}\) on the circle \(x^{2}+y^{2}=1\longrightarrow type1\)
Sol: Let \(g(x,y)=x^{2}+y^{2}\) and we get circle \(\Rightarrow\) \(g(x,y)=x^{2}+y^{2}=1\)
If \(\triangledown f(x,y)=\lambda \triangledown g(x,y)\), then \((f_{x},f_{y})=\lambda (g_{x},g_{y}) \Rightarrow (2x,4y)=\lambda (2x,2y)\)
\(\begin{cases}2x=2\lambda x\Rightarrow& 2x(\lambda-1)=0\Rightarrow x=0,\lambda=1\\4y=2\lambda y\Rightarrow & 2y=\lambda y\longrightarrow type2\end{cases}\)
If x=0, then \(type1 \Rightarrow y^{2}=1 \Rightarrow y=±1\Rightarrow(x,y)=(0,1)or(0,-1)\)
If \(\lambda\)=1, then \(type2 \Rightarrow2y=y\Rightarrow y=0\Rightarrow x^{2}=1\Rightarrow x=±1 \\\Rightarrow(x,y)=(1,0)or(-1,0)\)
| (x,y) | (0,1),(0,-1) | (1,0),(-1,0) |
|---|---|---|
| f(x,y) | 2,2 | 1, 1 |
| extremum | abs max value | abs min value |
簡言之
求解函數:\(z=f(x,y)\)在條件\(\phi(x,y)=0\)條件下的極值。
解:
- 建構函式\(F(x,y)=f(x,y)+\lambda\phi(x,y)\),其中\(\lambda\)為拉格朗日乘數
- 其中\((x,y)\)就是極值點座標
自變數多於兩個的條件下
函數:\(u=f(x,y,z,t)\)在條件\(\phi(x,y,z,t)=0, \Psi(x,y,z,t)=0\)下的極值
建構函式:\(F(x,y,z,t)=f(x,y,z,t)+\lambda_{1}\phi(x,y,z,t)+\lambda_{2}\Psi(x,y,z,t)\)
其中\(\lambda_{1},\lambda_{2}\)均為拉格朗日乘數,同樣通過偏導為0以及約束條件求解
如:
函數:\(u=x^{3}y^{2}z\),約束條件:\(x,y,z\)之和為12,求其最大值。
解:
-
建構函式:\(F(x,y,z)=x^{3}y^{2}z+\lambda(x+y+z-12)\)
-
分別求偏導:
-
唯一駐點:(6,4,2)
-
\(u_{max}=6^{3}\cdot 4^{2}\cdot 2=6912\)
例:
在第一卦限內作橢圓球面\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1\)的切平面,使切平面與三個座標面所圍成的四面體體積最小,求切點座標。
解:
設\(P(x_{0},y_{0},z_{0})\)為橢球面上的一點,令\(F(x,y,z)=\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1\)
則\(F^{'}_{x}|_{p}=\frac{2x_{0}}{a^{2}},F^{'}_{y}|_{p}=\frac{2y_{0}}{b^{2}},F^{'}_{z}|_{p}=\frac{2z_{0}}{a^{2}}\)
過\(P(x_{0},y_{0},z_{0})\)的切平面方程為
\(\frac{x_{0}}{a^{2}}(x-x_{0})+\frac{y_{0}}{b^{2}}(y-y_{0})+\frac{z_{0}}{c^{2}}(z-z_{0})=0\)
化簡為\(\frac{x·x_{0}}{a^{2}}+\frac{y·y_{0}}{b^{2}}+\frac{z·z_{0}}{c^{2}}=1\)
該切平面在三個軸上的截距各為\(x=\frac{a^{2}}{x_{0}},y=\frac{b^{2}}{y_{0}},z=\frac{c^{2}}{z_{0}}\)
所求四面體的體積\(V=\frac{1}{6}xyz=\frac{a^{2}b^{2}c^{2}}{6x_{0}y_{0}z_{0}}\)
在條件\(\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}=1\)下求V的最小值,
目標函數\(V=\frac{a^{2}b^{2}c^{2}}{6x_{0}y_{0}z_{0}}\), 約束條件\(\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}=1\)
令\(u=lnx_{0}+lny_{0}+lnz_{0}\)
\(L(x_{0},y_{0},z_{0})=lnx_{0}+lny_{0}+lnz_{0}+\lambda(\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1)\)
由\(\begin{cases}L^{'}_{x_{0}}=0,L^{'}_{y_{0}}=0,L^{'}_{z_{0}}=0\\\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1=0\end{cases}\)
\(L(x_{0},y_{0},z_{0})=lnx_{0}+lny_{0}+lnz_{0}+\lambda(\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1)\)
即\(\begin{cases}\frac{1}{x_{0}}+\frac{2\lambda x_{0}}{a^{2}}=0\\\frac{1}{y_{0}}+\frac{2\lambda y_{0}}{b^{2}}=0\\\frac{1}{z_{0}}+\frac{2\lambda z_{0}}{c^{2}}=0\\\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1=0\end{cases}\), 可得\(\begin{cases}x_{0}=\frac{a}{\sqrt{3}}\\y_{0}=\frac{b}{\sqrt{3}}\\z_{0}=\frac{c}{\sqrt{3}}\end{cases}\)
故當切點座標為\((\frac{a}{\sqrt{3}},\frac{b}{\sqrt{3}},\frac{c}{\sqrt{3}})\)
四面體的體積最小\(V_{min}=\frac{\sqrt{3}}{2}abc\)
拉格朗日對偶(Lagrange duality)問題
約束最佳化問題,形式如下(非這種形式也可以轉化為這種形式)
引入拉格朗日函數
\(L(x,\alpha,\beta)=f(x)+\displaystyle\sum\limits_{i=1}^k \alpha_{i}c_{i}(x)+\displaystyle\sum\limits_{j=1}^l \beta_{i}h_{i}(x)\)
\(
\alpha_{i}\geqslant0\)
定義\(\theta_{p}(x)=\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}L(x,\alpha,\beta)\)
若\(x\)違反原始約束條件,\(c_{i}(x)>0\)則讓\(\alpha_{i}\)為\(+\infty\),其他\(\alpha和\beta\)引數都為0,則\(\theta_{p}(x)=+\infty\)
若\(x\)違反原始約束條件,\(h_{i}(x)≠0\)則讓\(\beta_{i}h_{i}(x)=+\infty\),其他\(\alpha和\beta\)引數都為0,則\(\theta_{p}(x)=+\infty\)
若\(x\)違反原始約束條件,讓全部的\(\beta_{i}h_{i}(x)=0和\alpha_{i}c_{i}(x)=0,f(x)\)是一個與\(\alpha和\beta\)無關的常數,則\(\theta_{p}(x)=f(x)\),也就是\(\theta_{p}(x)=\begin{cases}f(x),x滿足原始問題約束\\+\infty,其他\end{cases}\)
原問題等價於:\(\min \limits_{x}\theta_{p}(x)=\min \limits_{x}\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}L(x,\alpha,\beta)\)
通過拉格朗日函數重新定義一個無約束問題,這個無約束問題等價於原來的約束優化問題,從而將約束問題無約束化。
原問題的對偶問題:
\(\theta_{d}(\alpha,\beta)=\min \limits_{x}L(x,\alpha,\beta)\)
\(\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\theta_{d}(\alpha,\beta)=\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\min \limits_{x}L(x,\alpha,\beta)\)
並且有\(\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\theta_{d}(\alpha,\beta)\leqslant\min \limits_{x}\theta_{p}(x)\)
也就是說原始問題的最優值不小於對偶問題的最優值,但是我們要通過對偶問題來求解原始問題,就必須使得原始問題的最優值與對偶問題的最優值相等,當原始問題與對偶問題的最優值相等時,原始問題和對偶問題的可行解就是最優解。
滿足什麼樣的條件才能使原始問題的最優值與對偶問題的最優值相等,KKT條件:
前面三個條件對應各個變數的偏導數為0(這裡需要假設三個函數連續可微,若不連續,這裡的偏導數存在與否就不能夠保證),後面四個條件就是原始問題的約束條件以及拉格朗日乘子需要滿足的約束,其中\(\alpha_{i}c_{i}=0\)為對偶互補條件。