連結串列
2022-07-10 12:00:14
連結串列
定義(單連結串列):
1.用一組地址任意的儲存單元存放線性表中的資料元素。
資料元素(資料域) + 指標(指標域,指示後繼元素儲存位置) = 結點
以「結點的序列」表示線性表——稱作連結串列。
2.以線性表中第一個資料元素「1」的儲存地址作為線性表的地址,稱作線性
表的首地址。 有時為了操作方便,會在第一個結點之前虛加一個「頭指標」。
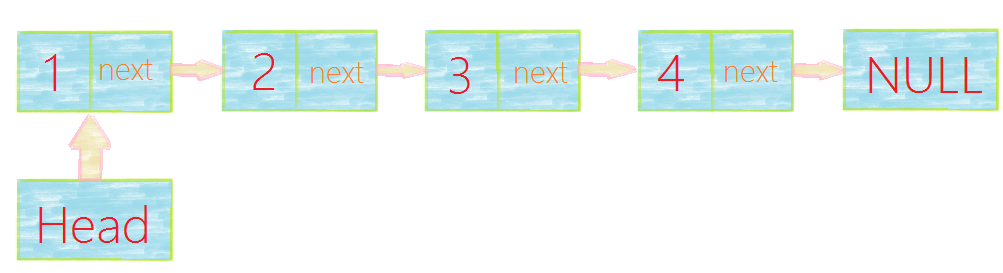
單連結串列的實現:
【題面描述】輸入一行整數存入連結串列中,「-1」為結束標誌,整數之間空格分開。
統計連結串列中數值為m的數的個數。
輸入:
1 1 1 2 3 4 5 -1
1
輸出:
3
#include<bits/stdc++.h> using namespace std; struct Node//定義連結串列結構 { int data; Node *next = NULL; }; Node *head,*r,*p; //定義頭指標/尾指標/操作指標 //2.查詢連結串列中存在m的數,統計個數 void search2(int xx){ int cnt=0; Node *p; p=head->next; //定位第一個開始 while(p!=NULL){ if(p->data==xx) cnt++; p=p->next; } cout<<cnt<<endl; } int main(){ int x; //每次要插入的資料 cin>>x; head=new Node;//建立新結點 並讓head頭指標指向 r=head; //因為只有1個結點,尾指標也指向它 while(x!=-1){ //讀入非-1的數值 p=new Node; //先申請新結點,後續再放數值 p->data=x; p->next=NULL; //每次新結點作為最後1個^ r->next=p; r=p; cin>>x; } int m; //查詢m cin>>m; search2(m); return 0; }
【題面描述】輸入一行整數存入連結串列中,「-1」為結束標誌,整數之間空格分開。
在第k個數前面,插入數值m。插入後再輸出該連結串列。
輸入:
5 4 8 8 -1
3 1
輸出:
5 4 1 8 8
#include<bits/stdc++.h> using namespace std; struct Node{//定義連結串列結構 int data; Node *next = NULL; };Node *head,*r,*p; //定義頭指標/尾指標/操作指標 void insert(int i,int x){ Node *p,*s; int j=0; p=head; while((p!=NULL)&&(j<i-1)){ p=p->next;//尋找i-1個結點,插在它後面 j=j+1; } if(p==NULL) cout<<"no this position!"; else{ s=new Node; s->data=x; //新結點賦值 s->next=p->next; p->next=s; } } void print(){ p=head->next; while(p->next!=NULL){ cout<<p->data<<" ";//輸出 p=p->next; } cout<<p->data<<endl; //最後一個結點 } int main(){ int x; //每次要插入的資料 cin>>x; head=new Node;//建立新結點 並讓head頭指標指向 r=head; //因為只有1個結點,尾指標也指向它 while(x!=-1){ //讀入非-1的數值 p=new Node; //先申請新結點,後續再放數值 p->data=x; p->next=NULL; //每次新結點作為最後1個^ r->next=p; r=p; cin>>x; } int k,m; //在第k個數前面,插入m結點 cin>>k>>m; insert(k,m); //插入操作 print();//輸出檢視 return 0; }
【題面描述】輸入一行整數存入連結串列中,「-1」為結束標誌,整數之間空格分開。
有Q次刪除詢問,每次刪除第m個結點。最後輸出詢問後的連結串列連結串列刪除操作。
輸入:
5 4 1 1 8 8 8 -1
2 4 4
輸出:
5 4 1 8 8
#include<bits/stdc++.h> using namespace std; struct Node{ //定義連結串列結構 int data; Node *next = NULL; }; Node *head,*r,*p; //定義頭指標/尾指標/操作指標 void del(int m){//刪除連結串列中第m個結點 Node *p,*s; int j=0; p=head; while((p->next!=NULL)&&(j<m-1)) { //先讓p定位到m的前一個位置 p=p->next; j=j+1; } if(p->next==NULL) cout<<"no this position!"; else { s=p->next; p->next=p->next->next; //上面也可:p->next=s->next free(s); } } void print(){ p=head->next; while(p->next!=NULL){ cout<<p->data<<" ";//輸出 p=p->next; } cout<<p->data<<endl; //最後一個結點 } int main(){ int x; //每次要插入的資料 cin>>x; head=new Node;//建立新結點 並讓head頭指標指向 r=head; //因為只有1個結點,尾指標也指向它 while(x!=-1){ //讀入非-1的數值 p=new Node; //先申請新結點,後續再放數值 p->data=x; p->next=NULL; //每次新結點作為最後1個^ r->next=p; r=p; cin>>x; } int Q; cin>>Q; //刪除Q次 while(Q--){ int m; //刪除連結串列中第m個結點 cin>>m; del(m); //刪除操作 } print();//輸出檢視 return 0; }
【題面描述】輸入一行整數存入連結串列中,「-1」為結束標誌,整數之間空格分開。
請編寫程式刪除表中所有數值為m的結點。最後輸出連結串列的長度。連結串列刪除操作
輸入:
5 4 1 8 8 2 2 -1
2
輸出:
5
#include<bits/stdc++.h> using namespace std; struct Node //定義連結串列結構 { int data; Node *next = NULL; }; Node *head,*r,*p; //定義頭指標/尾指標/操作指標 void del(int m){//刪除連結串列中數位m Node *p,*s; p=head; if(p->next->data==m) //P在m前面找到m p->next = p->next->next; //跨過m while(p->next!=NULL){ //先讓p定位到m的前一個位置 while(p->next!=NULL&&p->next->data == m ){ s=p->next; p->next=p->next->next; if( p->next == NULL ) break; free(s); } if( p->next == NULL ) break; p=p->next; } } int len( ){//現存的連結串列長度 int n=0; p=head; while(p->next!=NULL){ n=n+1; p=p->next; } return n; } int main(){ int x; //每次要插入的資料 cin>>x; head=new Node;//建立新結點 並讓head頭指標指向 r=head; //因為只有1個結點,尾指標也指向它 while(x!=-1){ //讀入非-1的數值 p=new Node; //先申請新結點,後續再放數值 p->data=x; p->next=NULL; //每次新結點作為最後1個^ r->next=p; r=p; cin>>x; } int m; //刪除連結串列中第m個結點 cin>>m; del(m); //刪除操作 cout << len();//輸出檢視 return 0; }
例題:
原題傳送門
P1996 約瑟夫問題
題目描述
n 個人圍成一圈,從第一個人開始報數,數到 m 的人出列,再由下一個人重新從 11 開始報數,數到 mm 的人再出圈,依次類推,直到所有的人都出圈,請輸出依次出圈人的編號。
注意:本題和《深入淺出-基礎篇》上例題的表述稍有不同。書上表述是給出淘汰 n-1 名小朋友,而該題是全部出圈。
輸入格式
輸入兩個整數 n,m。
輸出格式
輸出一行 n 個整數,按順序輸出每個出圈人的編號。
輸入輸出樣例
輸入 #1
10 3
輸出 #1
3 6 9 2 7 1 8 5 10 4
說明/提示
1≤m,n≤100
#include<bits/stdc++.h>//萬能頭. using namespace std; int m,n; struct Node{//定義頭指標,尾指標,操作指標. int data; Node *next; } *head,*p,*tail,*temp; int main(){ scanf("%d%d",&m,&n); head=new Node; head->next=NULL; tail=head; for(int i=1;i<=m;i++){ p=new Node; p->data=i; p->next=NULL; tail->next=p; tail=p; } p=head->next;/ tail->next=head->next;//連結串列首尾相連形成迴圈連結串列. for(int i=1;i<=m;i++){ for(int j=1;j<n-1;j++){ p=p->next; } cout<<p->next->data<<" "; temp=p->next; p->next=temp->next;//連線要刪除那個結點上下結點 p=p->next;//更新 free(temp);//釋放空間 } return 0; }
連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列連結串列