從傅立葉級數（Fourier series）到離散傅立葉變換（Discrete Fourier transform）

一. 傅立葉級數（FS）

首先從最直觀的開始，我們有一個訊號\(x(t)\)（滿足Dirichelet條件），先假設它是週期的，為了研究它，我們使用級數將之展開，展開方法如下

\[x(t)=\sum_{k=0}^{\infty}a_ke^{jkw_0t}\tag{1} \]

現在問題就是如何求解\(a_k\)。因為三角函數是正交系，即

\[\forall \theta_1 \ne \theta_2 ,都有\int_{2\pi}e^{j(\theta_1 - \theta_2)t}\mathrm{d}t=0 \tag{2} \]

這樣我們就可以進行如下操作：

對（1）式左右同時積分：

\[\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t=\sum_{k'=o}^{k=\infty}\int_{T}a_ke^{j(k'-k)\frac{2\pi}{T_0}}\mathrm{d}t \tag{3} \]

由於

\[\sum_{k=o}^{k=\infty}\int_{T}a_ke^{j(k'-k)\frac{2\pi}{T_0}}\mathrm{d}t=\begin{cases} 0,& k\ne k'\\ T,&k=k' \end{cases}\tag{4} \]

故（3）積分的結果如下：

\[\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t =a_kT \]

於是我們得到了\(a_k\)：

\[a_k=\frac{1}{T}\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t \tag{5} \]

這樣我們就把一個週期訊號分解成了一系列模為\(a_k\)的復週期訊號的組合，形象表示就是這樣：

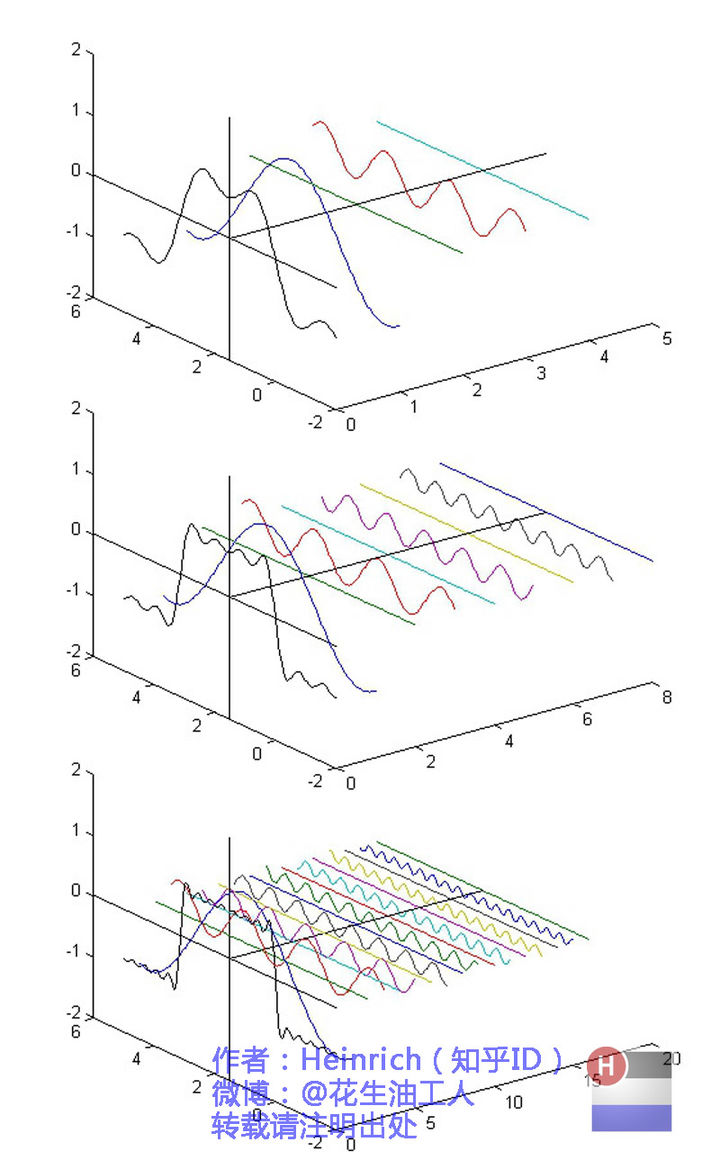
圖片來源：傅立葉分析之掐死傅立葉教學https://zhuanlan.zhihu.com/p/19763358（推薦大家看看）

OK，到這裡我們成功將一個週期訊號分解成了傅立葉級數。但是這裡也有兩個問題依然困擾著我：

1.首先（相信大家也注意到了我第一句標黃的內容），非週期有限訊號能不能展開成傅立葉級數呢？

比如，如果有一個函數，它是這樣的：

\[s(t) = \begin{cases} x(t), & 0\le t \le T \\ 0, & others \\ \end{cases}\\ \tag{6} x(t)是一個週期為T，滿足Dirichelet條件的函數 \]

我們同樣可以在0-T上做積分，並且得到\(s(t)\)的\(a_k\)和\(x(t)\)的\(a_k\)是相同的，也就是說，可以把s(t)寫成：

\[s(t)=\begin{cases} \sum_{k=0}^{\infty}a_ke^{jkw_0t},& 0\le t\le T\\ 0,& others \end{cases} \tag{7} \]

但是咱也理解，這樣的一個式子大概率不能叫做級數，充其量叫個級數的一部分。不過我們主要研究訊號，就不關心這些數學概念了。那麼對於這樣的一個訊號，傅立葉級數還能不能表達它的頻譜特性呢？它的頻譜跟\(x(t)\)又有什麼聯絡呢？,這兩個問題我們在第二部分解答。

2. 三角函數系的正交性強調的是一個週期內的積分，但是沒有說一定是最小正週期，如果我們在\(2T\)、\(3T\)或者\(nT\)上積分，會發生什麼呢？

回答這個問題之前，我們先對傅立葉級數做一個比較統籌的顯示，我們不妨以\(w\)作為橫座標，以\(a_ke^{jkw_0}\)的強度（也就是\(||a_ke^{jkw_0}||=|a_k|\)）作為縱座標，構建一個二維直角座標系(資料大小是隨便給的)：

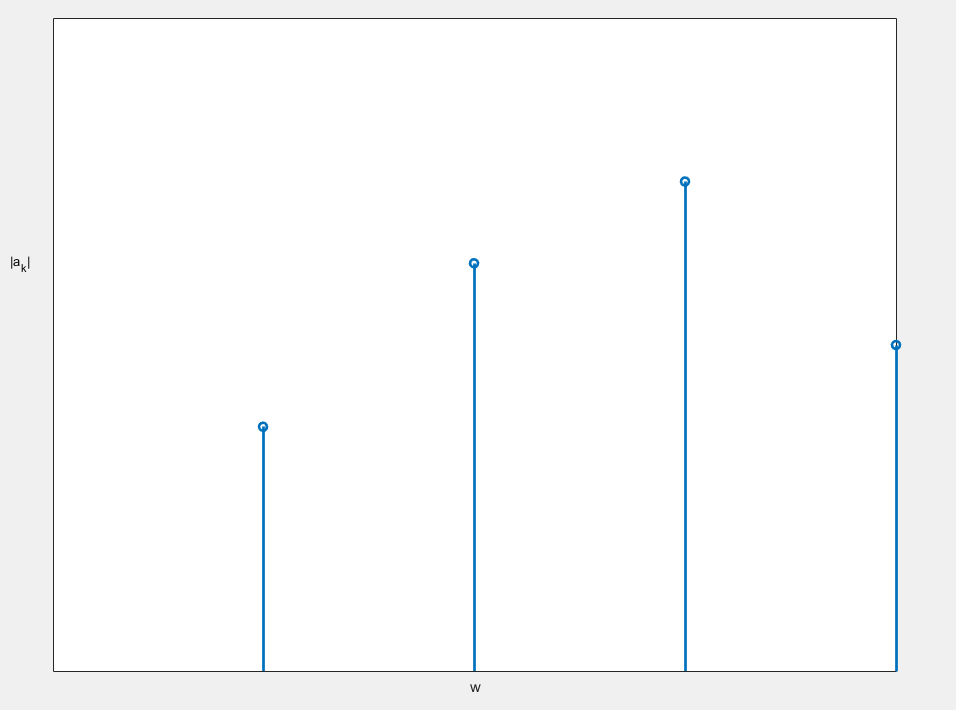
分析這個圖，我們知道每兩個」柱子「之間的距離應該是\(\Delta w=w_0=\frac{2\pi}{T}\)，所以，如果我們增大T，兩個資料之間的距離就會變小，如下：

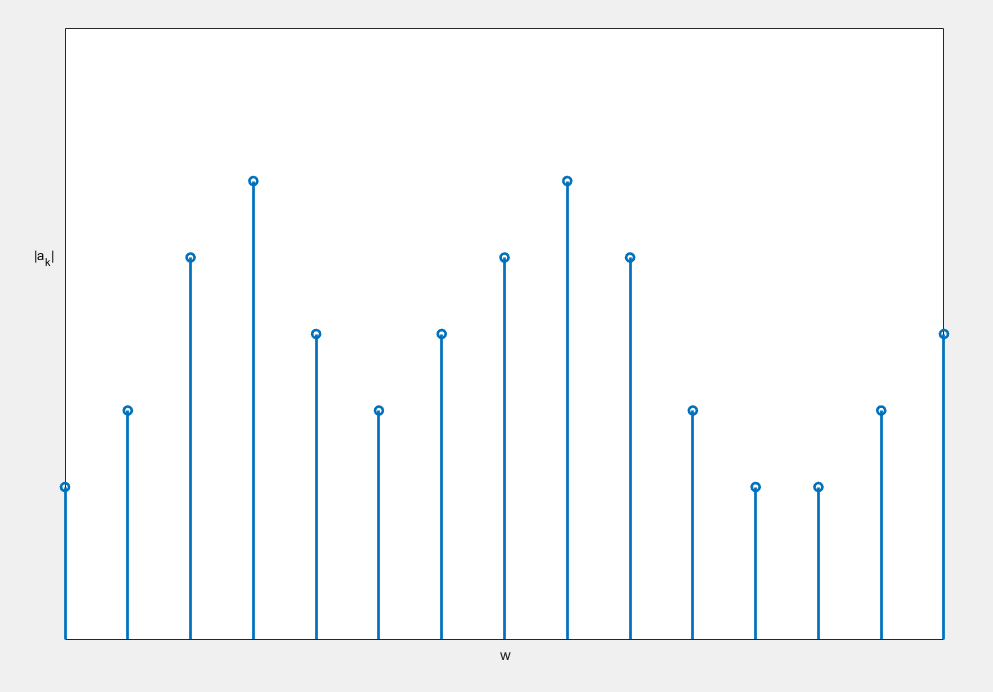
可以看到，\(T\)越大,兩個資料之間的橫軸距離就越小，不妨做個猜想：當\(T\to \infty\)時，這個離散的譜就變成了連續譜。是這樣嗎？應該說對有限訊號是這樣的，對無限週期訊號則不是，這是為什麼呢？請看下一節傅立葉變換的解讀。

二. 傅立葉變換（FT）

2.1 傅立葉變換的推導

接著前面的猜想進行分析，為了得到可靠結論，我們進行如下數學分析：

接著（5）式開展：

\[a_k=\lim_{T\to \infty}\frac{1}{T}\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t \]

用\(w_0=\frac{2\pi}{T}\)替代\(T\)，同時將\(x(t)\)表示出來:

\[\begin{split} x(t)&=\sum_{k=0}^{\infty}[\lim_{T\to \infty}\frac{1}{T}\int_{-\infty}^{+\infty}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t]e^{jk\frac{2\pi}{T}t} \\ &=\sum_{k=0}^{\infty}\lim_{w_0\to 0}[\frac{w_0}{2\pi}\int_{-\infty}^{+\infty}x(t)e^{-jkw_0t} \mathrm{d}t]e^{jkw_0t}\\ \end{split} \]

當\(w_0\to 0\)時，可用\(w_0=\mathrm{d} w\)表示它，此外，對於\(kw_0\)的累加就變成了積分（累加步長\(kw_0\)無限小）,故而上式變成了：

\[x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t]e^{jwt}\mathrm{d}w \]

這樣我們實現了將一個訊號分解成連續的頻譜，而這個頻譜就是：

\[X(w)=\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t \\ x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(w)e^{jwt}\mathrm{d}w \tag{8} \]

（6）式就是傅立葉變換的基本形式，當然有些地方可能將係數\(\frac{1}{2\pi}\)進行了一些變換,比如：

\[X(w)=\sqrt{ \frac{1}{2\pi} }\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t \\ x(t)=\sqrt{ \frac{1}{2\pi} }\int_{-\infty}^{+\infty}X(w)e^{jwt}\mathrm{d}w \]

這些都是小細節，咱們就不在意了。

2.2 周期函數的傅立葉變換

觀察（8）這個式子，我們很快又發現了另外一個問題，積分割區域是無窮，而周期函數在無窮區間積分，那必然是發散的，怎麼解呢？

我們是這樣處理的：

首先將\(x(t)\)表示成傅立葉級數：

\[x(t)=\sum_{k} a_ke^{jkw_ot} \]
對級數做傅立葉變換，也就是：

\[X(w)=\sum_{k} F(a_ke^{jkw_ot})=a_k\sum_{k} F(e^{jkw_0t})\tag{9} \]

於是問題轉化成了如何求\(e^{jkw_0t}\)的傅立葉變換，這個就要使用傅立葉變換的基本性質了：訊號乘以\(e^{jw_0t}\)相當於傅立葉變換\(X(w)\)進行頻移\(w_0\)，這個我們也可以順便證明一下：

\[若X(w)=\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t \\ \begin{split} 則X'(w)&=\int_{-\infty}^{+\infty}[x(t)e^{jw_0t}]e^{-jwt} \mathrm{d}t\\ &=\int_{-\infty}^{+\infty}x(t)e^{-j(w-w_0)t} \mathrm{d}t\\ &=X(w-w_0) \end{split} \]

又由於：

\[1=\frac{1}{2\pi}\int_{-\infty}^{+\infty}2\pi \delta (t)e^{jwt}\mathrm{d}w \\ 故F(x)=2\pi \delta (t) \]

所以：

\[F(1\cdot e^{jkw_0t})=F_{w-w_0}(1)=2\pi \delta (w-w_0)\tag{10} \]

把（10）代入（9），就得到了周期函數的傅立葉變換：

\[X(w)=a_k\sum_{k} 2\pi \delta(w-kw_0)\tag{11} \]

可以看出，周期函數的傅立葉變換是一系列衝擊串，這個倒也符合我們的直覺：

傅立葉變換每個\(X(w)\)可以理解為訊號頻率為\(w\)的分量的大小，對於週期訊號，它的每一個頻率分量都是一個無限長訊號，所以每一個分量的能量都是無窮的，所以在頻譜上就表示為衝擊串了。

2.3 有限長非週期訊號的傅立葉變換

好了，現在我們來解答第一節中的第二個問題：有限長非週期訊號的傅立葉變換和週期訊號頻譜的關係。

對於有限長訊號：

\[s(t) = \begin{cases} x(t), & 0\le t \le T \\ 0, & others \\ \end{cases}\\ \tag{6} x(t)是一個週期為T，滿足Dirichelet條件的函數 \]

可以換一種表達方式:

\[s(t)=x(t)[u(t)-u(t-T)] \]

要求\(F[s(t)]\)，我們首先需要以下幾個結論：

時域相乘等於頻域折積，證明:

\[若Z(w)=X(w)*Y(w),則\\ \begin{split} z(t)&=F^{-1}(Z(w))\\ &=\int_\infty [\int_\infty X(m)Y(w-m)\mathrm{d}m]e^{jwt}\mathrm{d}t \\ &=\int_\infty X(m)[\int_{\infty}Y(w-m)e^{jwt}\mathrm{d}t]\mathrm{d}m\\ &=\int_\infty X(m)y(t)e^{jmt}\mathrm{d}m\\ &=x(t)y(t)\\ 得證 \end{split} \]
注：如果從採用\(z(t)=x(t)y(t)出發，去證明Z(w)=X(w)*Y(w)\)會比較麻煩。
\(F[u(t)-u(t-T)]=\frac{1-e^{-jwt}}{jw}\)，這個就很好證明了:

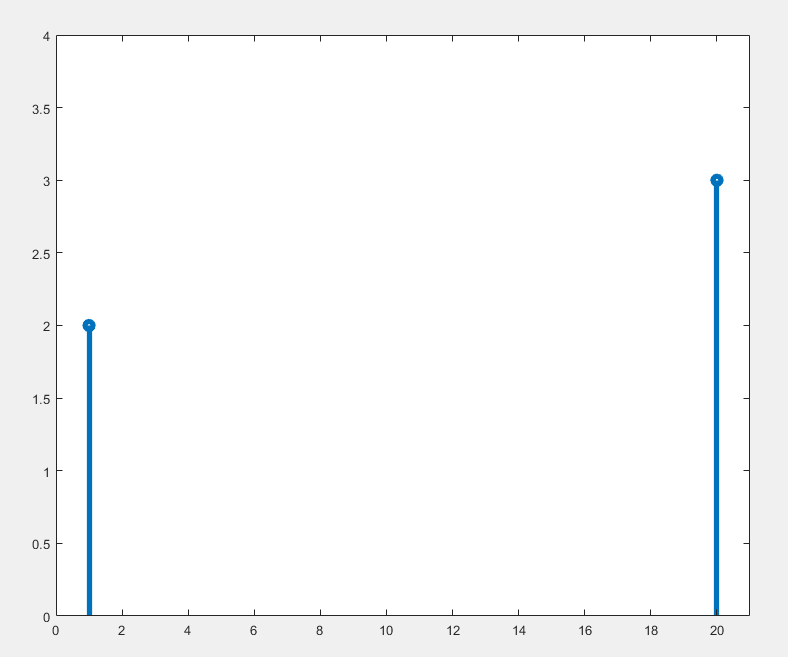
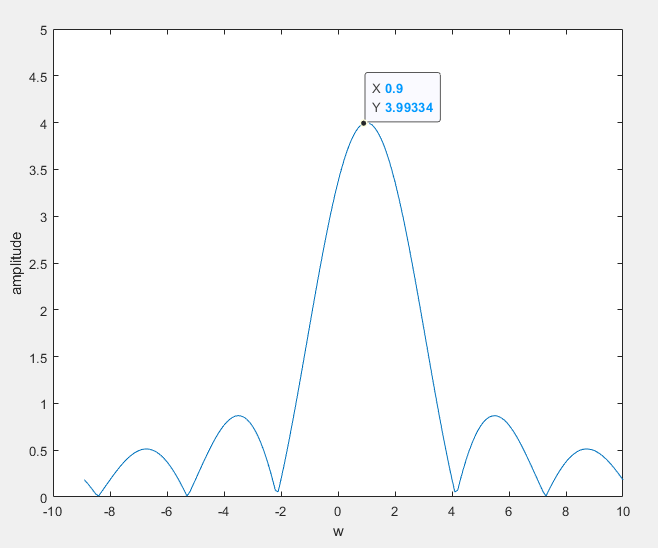
\[\begin{split} F[u(t)-u(t-T)]&=\int_{0}^{T}x(t)e^{-jwt}\mathrm{d}t\\ &=\frac{1-e^{-jwt}}{jw} \end{split} \]
這個函數展現的頻譜影象如下：

好了，我們現在可以開始計算（6）式\(s(t)\)的傅立葉變換了：

\[F(s(t))=F(x(t))*F[u(t)-u(t-T)]\\ 在(11)有X(w)=a_k\sum_{k} 2\pi \delta(w-kw_0)\\ 故F(s(t))=2\pi a_k\sum_{k}\delta(w-kw_0)*\frac{1-e^{-jwt}}{jw}\\ 又有\delta (t-t_0)*x(t)=x(t-t_0) \]

及\(\sum_{k}\delta(w-kw_0)*\frac{1-e^{-jwt}}{jw}\)就是\(F[u(t)-u(t-T)]\)以\(kw_0\)移位疊加,一些一組圖表示這個過程：

簡單起見，我們令|X(w)|為：

對它進行折積，也就是將下面兩個訊號疊加：

於是得到|S(w)|：

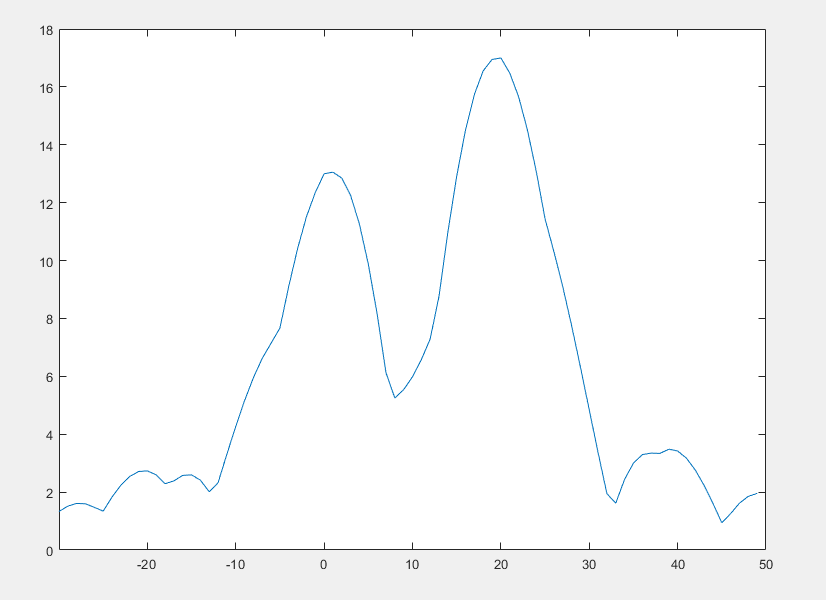
圖不咋好看，可能是頻率解析度沒調好，但是大概樣子大家能看清楚了，也就是在週期訊號的頻譜裡的衝擊串變得平滑了，或者換句話說，原來集中在某個\(kw_0\)頻率的能量一部分洩露到了全頻域。

這個在物理意義上也比較好理解，把週期訊號截斷了，實際上是把一部分訊號值變成了0，從某個值突然變到0(x(T)->0)，這裡沒有平滑過渡，是一個突變，而我們知道，突變包含所有頻率分量。

至此，我們完成了傅立葉級數到傅立葉變換的推導。

三、時域離散化

在實際應用中，我們大多處理的是數位訊號，也就是時域離散的訊號，我們來看看時域離散對訊號頻譜的影響。

這個時候，我們可以把訊號表示為

\[x(n)=x(t)\sum_{n=-\infty}^{+\infty}\delta(t-nT)\\ x(t)是連續訊號，T是取樣週期（即每隔T時間從x(t)上取一個點） \]

根據（10），利用傅立葉變換的對偶性，可以得出：

\[F(\sum_{n=-\infty}^{+\infty}\delta(t-nT))=w_0\sum_{k=-\infty}^{+\infty}\delta(w-kw_0)\\ w_s=\frac{2\pi}{T} \]

所以\(x(t)\)的傅立葉變換為：

\[F(x(n))=w_s\sum X(w)*\delta (w-kw_s)=w_s\sum X(w-kw_s)\\ X(w)是x(t)的傅立葉變換 \]

也就是說，\(x(n)\)的傅立葉變換就是下\(x(t)\)的傅立葉變換以\(w_s\)為週期，移位疊加。

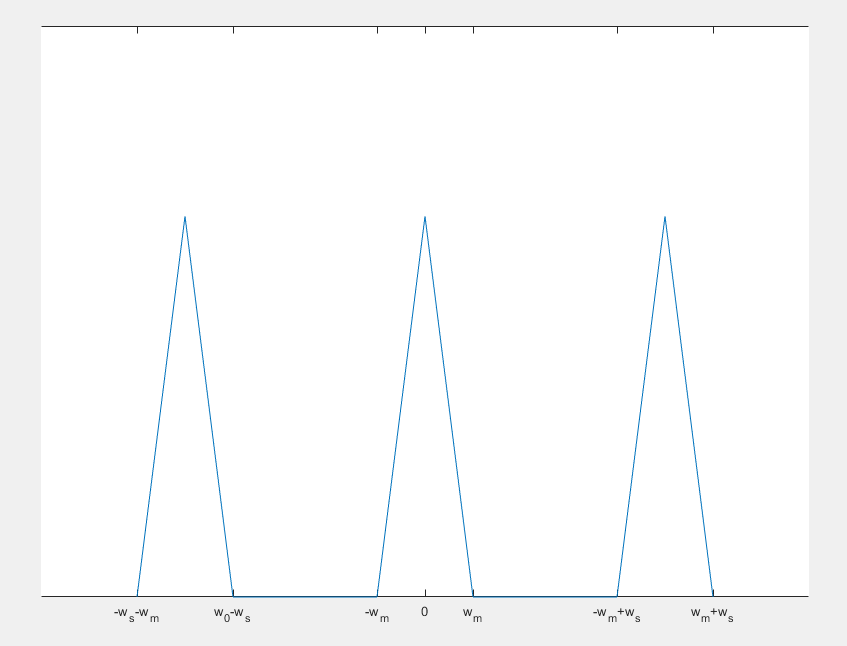
如上圖，假設中間的三角形就是\(X(w)\)，則它經過移位疊加後得到的上圖就是\(F(x(n))\)。

從這張圖我們也可以看出一個重要的定理——奈奎斯特取樣定理：取樣頻率需要高於訊號最高頻率的兩倍，因為如果不能滿足

\[w_m < w_s-w_m,即w_s>2w_m \]

就會發生頻譜混疊（上圖的兩個相鄰三角形疊在一起了）。

這樣我們就得到了時域離散訊號的傅立葉變換，但是顯然，這樣得到的頻譜也是連續的，計算機儲存的是離散訊號，那麼如何將頻域也離散化呢？請看下節。

四、DFT

回顧前面的內容，我們發現，滿足頻域離散的只有一種訊號，那就是週期訊號。於是讓訊號離散化的方法就呼之欲出了：

假設我們採集到的N個資料其實是一個週期訊號的一個週期，或者換句話說，我們把這N點資料以N為週期進行延拓，那麼接下來要做的就是對一個週期訊號的傅立葉變換了，又時域是離散的，傅立葉變換就退化成了傅立葉級數形式：

\[F(x(n))=\sum_{n=0}^{N-1}x(n)W_N^{nk}\\ W_{N}^{nk}=e^{-j\frac{2\pi}{N}nk}（為什麼要搞出個W_{N}^{nk}呢？我也不知道） \]

現在好了，時域和頻域都是離散的了，而且頻域和時域一樣只有N個點。並且通過上面時域離散造成頻域以取樣角頻率\(w_s\)拓展的結論，我們可以知道，這個數位頻譜，其實就是在長度為\(w_s\)的區間內插入了N個點，所以沒兩個點之間的頻率間隔為

\[\Delta w=\frac{w_s}{N} \]

這個\(\Delta w\)也叫做頻率解析度，也就是通過這個頻譜能區分的兩個頻率最小的間隔。

這裡我們再對模擬角頻率\(\Omega\)和數位角頻率做一個區分：

在模擬域，頻率\(f\)表示的是一個訊號每秒重複變化的次數，模擬角頻率\(\Omega=2\pi f\)表示的就是單位時間內訊號相位角變換的弧度。可以把一個重複的訊號想象成一個點做圓周運動，\(f\)表示它單位時間繞了多少圈，\(w\)表示它單位時間轉過多少弧度。

在數位域，我們同樣可以通過單位時間訊號相位角的該變數來表示角頻率，但是數位域只有單位1，無連續時間的概念，長度為N的序列，兩個點相隔的時間是\(\frac{1}{f_s}\)，所以數位域的「時間」每改變1，角度改變應該是：

\[\begin{split} w&=\Omega \frac{1}{f_s}\\ &=\Omega T \end{split} \]

上式還可以寫作\(w=2\pi \frac{f}{f_s}\)，又由取樣定理知\(f_s>2f\),所以\(w<\pi\)，但是我們常常取數位頻域的\(0-f_s\)進行研究，也就是說\(w\)最大取到\(2\pi\)(實際上是0移位一個週期得到的)，可見：\(w\)被限制在了[0 \(2\pi\)]，所以我們也稱數位角頻率\(w\)為歸一化頻率。

其實上述所有的推導都能在《訊號與系統》和《數位訊號處理》教材裡找到，我只是做了一個整理和總結，建議大家還是精讀課本，寫書的人一般比寫部落格的人強。