程式分析與優化
本章是系列文章的第十章,主要介紹CPU流水線、超標量體系架構等硬體設計,和編譯器怎麼使能這些功能來減少計算的時鐘週期。
本文中的所有內容來自學習DCC888的學習筆記或者自己理解的整理,如需轉載請註明出處。周榮華@燧原科技
10.1 概念
- 指令級並行是是讓一個程式中的多個操作同時執行的方法
- 指令級並行對原生的順序程式也能帶來並行效果
- 使能指令級並行的方法:
- 指令流水線,一起觸發一條指令,但多條指令的執行時間可以重疊
- 超標量體系架構執行:一條指令裡面由多條標量指令打包而成觸發的並行執行
10.2 熱身
對下面的c程式碼:
1 void swap(int v[], int k) { 2 int temp; 3 temp = v[k]; 4 v[k] = v[k + 1]; 5 v[k + 1] = temp; 6 }
有兩種組合編譯結果。A1:
1 lw $t0, 0($t1) # reg $t0 (temp) = v[k] 2 lw $t2, 4($t1) # reg $t2 = v[k + 1] 3 sw $t2, 0($t1) # v[k] = reg $t2 4 sw $t0, 4($t1) # v[k + 1] = reg $t0 (temp)
A2:
1 lw $t0, 0($t1) 2 lw $t2, 4($t1) 3 sw $t0, 4($t1) 4 sw $t2, 0($t1)
哪種效能更好?
其實上面兩種結果主要體現在第3條指令和第4條指令,是相反的。
要弄清這個問題,還得從CPU的指令流水線說起。
10.3 指令流水線
Instruction pipelining - Wikipedia中對指令流水線的概念做了一些掃盲,總結下來就是下面這張圖:

10.3.1 指令流水線的原理
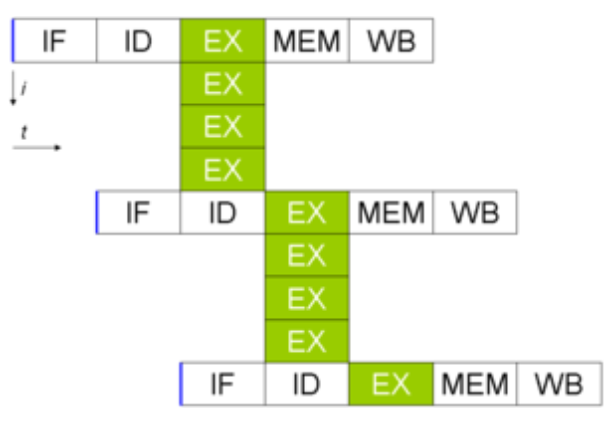
常見的指令流水線的前提是一個指令執行過程中能被切割成好幾塊,當前主流的做法是切分成5個時鐘週期來執行,也稱為經典RISC流水線。在這個流水線中一條執行時間是5個時鐘週期,但執行5個指令也只需要7個時鐘週期,相對不做指令級並行的時候5*5=25個時鐘週期而言,並行效果不言而喻。
10.3.1.1 IF
指令獲取,Instruction Fetch,從程式碼段中獲取指令。
10.3.1.2 ID
指令解碼,Instruction Decode,計算機體系架構設計上,除了軟體介面指令集外,最核心的就是微架構,所以一般軟體生成的指令,還需要翻譯成機器能識別的微指令,這樣才能真正執行。
10.3.1.3 EX
執行,Execute。
10.3.1.4 MEM
存取記憶體,Memory Access。
10.3.1.5 WB
暫存器回寫。
有很多處理器的流水線不是固定的,例如 Intel Pentium 4,由於x86是CISC,每個指令的長度本身就不一樣,實際實現是指令的執行週期也不完全一樣,Pentium 4的指令執行週期有的要7步,甚至最長20步的,但設計原理是類似的Recap13.ppt (live.com):

這些的並行的步驟,每個CPU(核)每次只能執行每類小步驟中的一步,不同類的小步驟是可以並行執行的,靠著將指令執行過程中的每個小步驟錯開並行起來,就實現了指令流水線的功能。
如果指令的總的執行時間是固定的,那麼切分出來的步驟越多,那並行效果就會越好,效能越好。
但是步驟越多,讓程式能指令級並行起來,編譯器的邏輯就越複雜,這種20步的流水線,估計得被編譯器團隊給噴死,所以後面x86體系架構再也沒有突破20步 :)。
10.3.2 資料衝突
指令流水線能並行執行的前提是指令間沒有資料衝突。如果指令I1的輸入依賴指令I2的輸出,那在I2執行完之前I1是沒法執行的,這就是資料衝突的含義。資料衝突太多,就會造成編譯器無法生成並行度很高的指令流水線序列,這種情況就會造成指令流水線熄火。
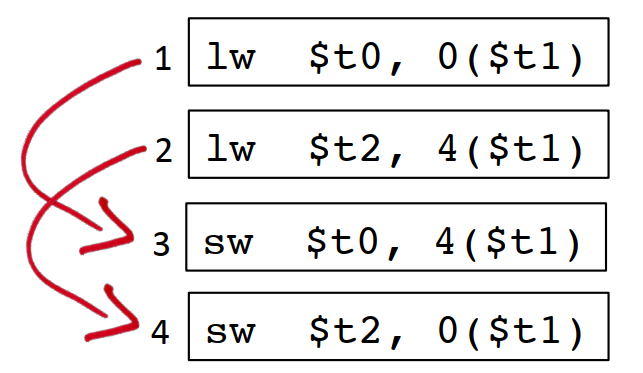
回到上面的例子,如果把$t2暫存器的讀指令和寫指令放到一起,那這2個指令就會造成指令流水線熄火:

相反,如果把t0和t2暫存器的讀寫操作插花式排列開來,如果是2步的流水線,可以完全不熄火,對3步的流水線,最多隻會熄火一步,所以後面這種插花的方式效能更好:
10.3.3 資料轉發
如果某條指令的輸出正好是後面指令的輸入,處理器可以直接將結果轉發給後面的指令:
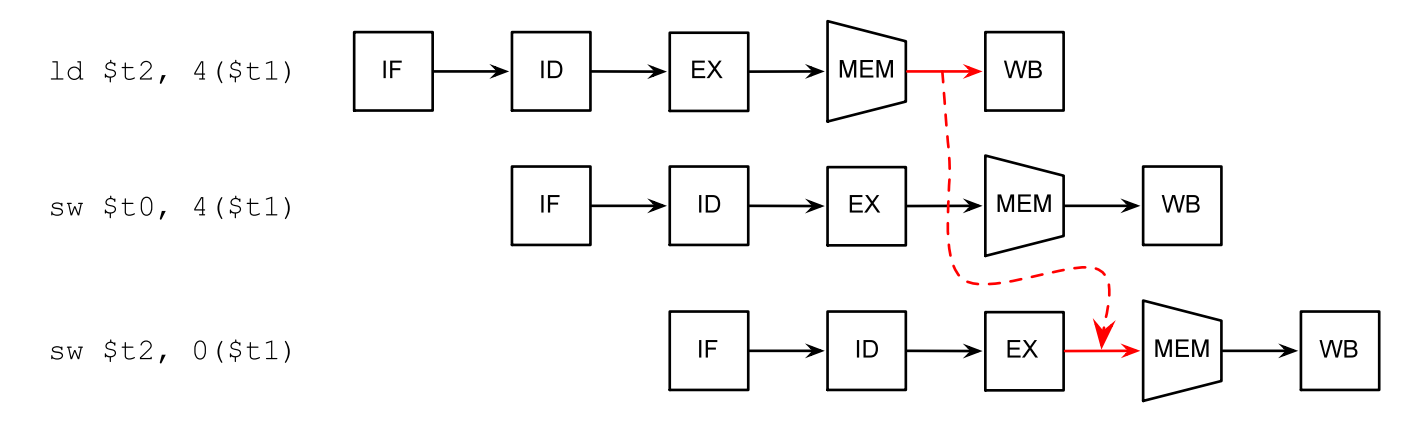
如果實在沒辦法,編譯器會插入一些no-op指令,讓處理器「怠速」一個時鐘週期:
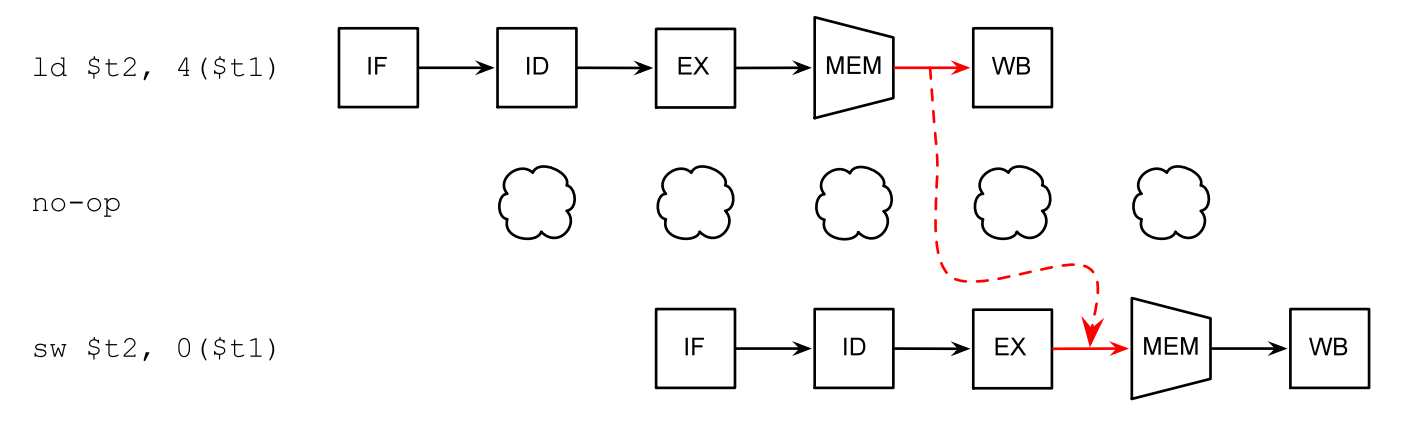
10.4 超標量體系架構
除了指令之間的流水線,超標量體系架構依賴指令內部的多條子指令之間的流水線來達到並行的效果。超標量體系架構其實依賴的是單個處理器中的多個IP(這裡的IP不是TCP/IP協定棧裡面的ip地址,是intellectual property的簡稱,是處理器裡面可以用來拼裝成一個大的處理的積木塊,也是可以獨立執行的處理單元)相互獨立執行來實現的。例如一個VLIW(Very Long Instruction Words,超長指令字)裡面可能既有主cpu的操作命令,也有DMA處理器的操作指令。一條GPU的指令裡面,可能既有控制指令,也有資料指令。
10.5 暫存器和並行
暫存器導致的依賴分三種(下面的讀、寫都是相對於暫存器來說的):
- 真實依賴,先寫後讀
lw $t0, 0($t1)
st $t0, 4($t1)
-
反依賴,先讀後寫
st $t0, 4($t1)
lw $t0, 0($t1)
- 輸出依賴,連續寫
lw $t0, 0($t1)
lw $t0, 4($t1)
除了第一種,後面兩種如果暫存器數量足夠的情況下,可以通過分配額外的暫存器來消除依賴。
暫存器分配演演算法讓我們儘可能的少用暫存器,但多個變數複用同一個暫存器的做法又會額外注入資料依賴,使相關程式碼無法並行執行。
以(a + b) + c + (d + e)為例,預設暫存器分配演演算法結果是這樣的:
1 LD r1, a 2 LD r2, b 3 ADD r1, r1, r2 4 LD r2, c 5 ADD r1, r1, r2 6 LD r2, d 7 LD r3, e 8 ADD r2, r2, r3 9 ADD r1, r1, r2
這樣分配的結果,導致這些指令能並行的可能性非常小,僅1/2和6/7這種連續的LD指令可以並行,其他都必須等上一行執行完才能開始執行,9條指令需要7條指令順序執行的時間。
但我們通過抽象語法樹的分析看,d+e的計算,其實和這之前的兩次加法也是不相干的,也可以並行;5個變數的LD指令,如果暫存器數量足夠的情況下,也可以並行。

理想的並行結果是這樣,只需要4條指令的執行時間就可以把這個計算完成:

怎麼樣儘可能並行的前提下,減少暫存器的使用?
10.6 基本塊排程
基本塊排程(Basic Block Scheduling)也稱本地排程(Local Scheduling)。主要使用指令依賴圖(有的地方也稱為資料依賴圖)來進行分析,程式中的每條指令是一個節點,如果節點i1使用節點i0定義的變數,則存在一條邊(i0, i1)。指令依賴圖IDG中的每條邊是一個delay,決定了最終至少需要多少個時鐘週期才能完成程式執行。
以下面的程式為例:
1 LD R2, 0(R1) 2 ST 4(R1), R2 3 LD R3, 8(R1) 4 ADD R3, R3, R3 5 ADD R4, R3, R2 6 ST 12(R1), R4 7 ST 0(R7), R7
假定每條LD/ST指令需要5個時鐘週期(除非LD指令緊接著ST指令,並且兩個指令操作同一個記憶體地址,這種情況下ST指令只需要3個時鐘週期),每條算術執行需要2個時鐘週期,算一下該程式需要多少時鐘週期?指令依賴圖可以這樣畫:

但即使不存在資料依賴,如果多個指令使用同一個資源,也需要排隊,所以如果先排程LD R2, 0(R1)的話,需要的時鐘週期是5+3+5+2+2+3+1=21個:

而先排程LD R3, 8(R1)的話,需要的時鐘週期是5+5+3+3+1=17個。

演演算法描述如下:
1 RT = empty reservation table 2 foreach vn ∈ V in some topological order: 3 s = MAX {S(p) + de | e = p→n ∈ E} // 對所有n的前驅p,求p的執行開始時間和p到n之間的delay,並在其中取最大值,也就是節點n的執行開始時間 4 let i = MIN {x | RT(n, j, x) ∈ RT} in 5 s' = s + MAX(0, i – s) 6 RT(n, j, s') = vn // 在所有可獲得的RT資源中,取高度最小的一個資源申請表,來排程n
下面是龍書上的演演算法描述,可以對照起來看:

生成的資源排程圖如下:
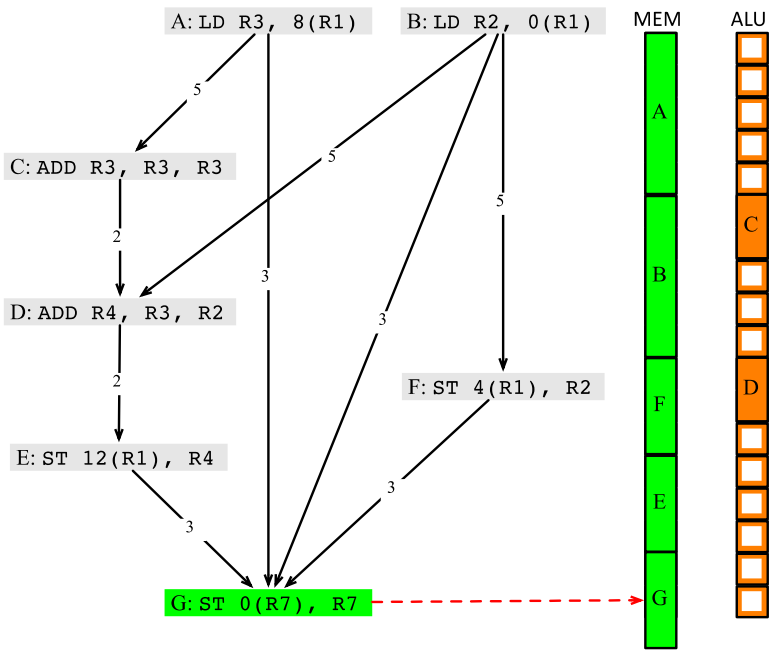
10.7 全域性程式碼排程
先看一個簡單的例子:
1 if (a != 0) { 2 c = b 3 } 4 e = d + d
優化前後的指令如下,紅色部分是做了指令移動的程式碼:
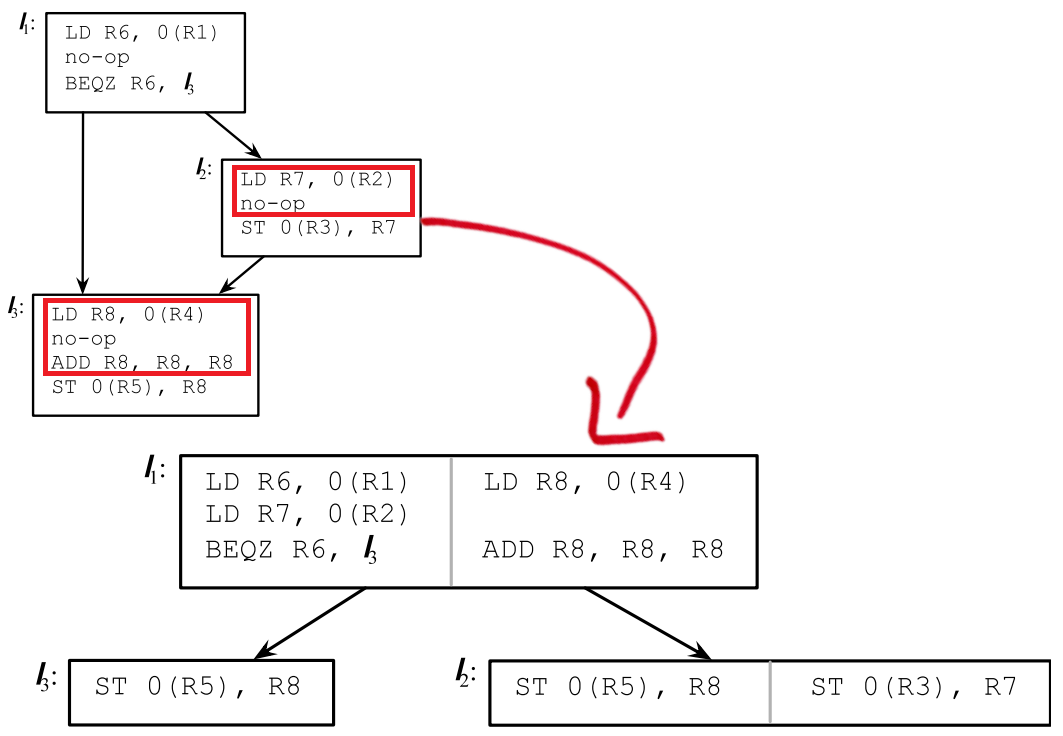
上面每個框裡面有個灰色的線,將兩塊指令放在了一起,在普通體系架構下,只是簡單的將他們進行流水線排序,如果在VLIW體系架構下,實際上是可以真正並行執行的,帶來的效果類似這樣:
實際上全域性程式碼排程相對於一個基本塊內的排程要複雜得多,主要涉及程式碼移動,不安全的決策,額外執行了可能不需要的指令等問題。
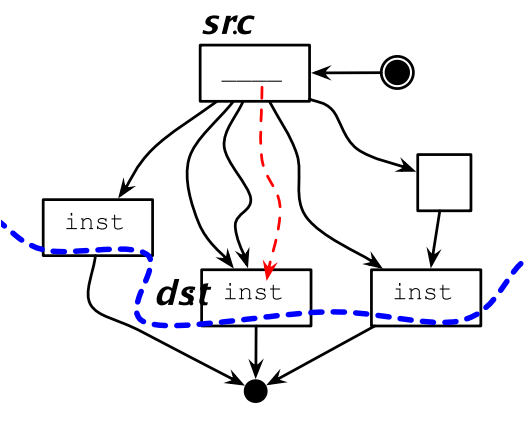
後支配(Postdominate):如果一個節點dst到程式終止的所有路徑都要經過節點src,則稱為src對dst有後支配關係。
控制流一致性(Control Equivalence):如果dst支配src,並且src後支配dst,則說明src和dst是控制一致的。
如果程式碼移動前後對應的位置具有控制流一致性,則這種遷移理論上是安全的。
10.7.1 程式碼上移
相應的,如果上移的程式碼不具備後支配性,則可能在某些場景下會多執行程式碼。
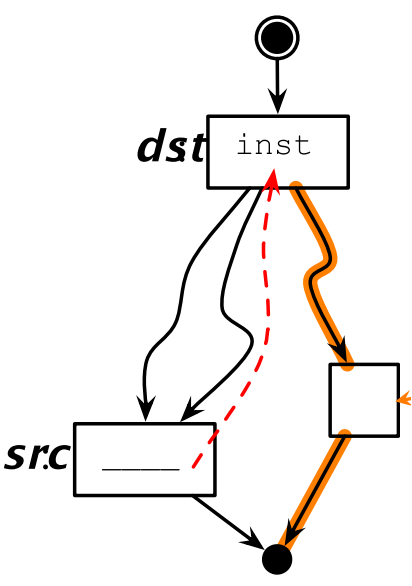
同樣的,如果上移的程式碼不是源位置的支配節點,則需要在其他路徑上插入補償程式碼,來確保上移的程式碼在各種場景下都能執行到。
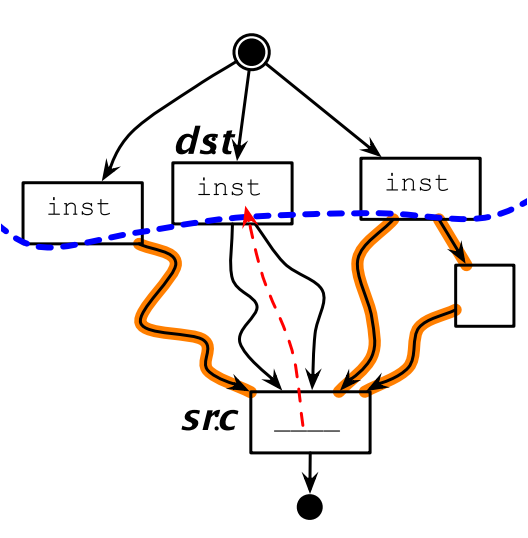
10.7.2 程式碼下移
如果src不是dst的支配節點的話,下移程式碼可能會覆蓋另外一個分支的值:

下行程式碼遷移也會有補償程式碼的問題:
10.7.3 超級塊
超級塊是將多個基本塊合併成的一個新的基本塊。
例如對下面4個基本塊:
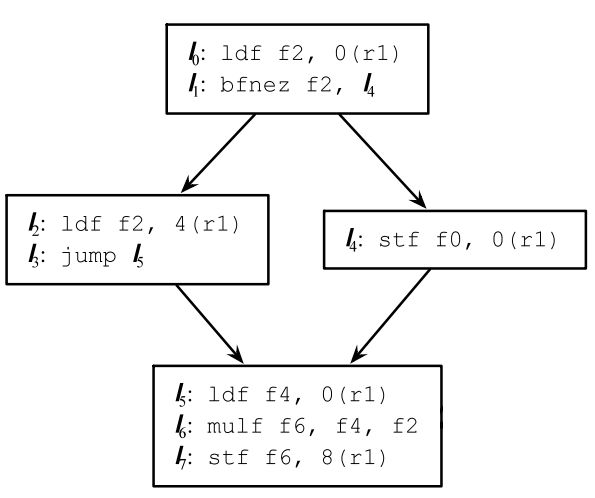
通過合併可以變成2個基本塊,少了3次跳轉指令,流水線就能更快的優化執行:

超級塊的生成過程更通用一點的做法就是把DAG轉換成樹的過程:

10.7.4 靜態profiling技術
通過一些先驗的概率,推斷某些分支走到的可能性,來優化概率更高的分支執行速率的方法。
但多個先驗概率有可能是相互矛盾的,有時需要在多個先驗概率直接做一些妥協,或者計算加權概率,最有名的是Dempster-Shafer定理:
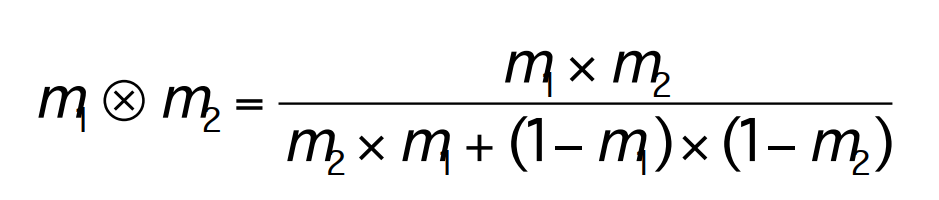
10.8 指令級並行研究歷史
- Hennessy, J. L. and D. A. Patterson, Computer Architecture: A Quantitative Approach, Third Edition, 2003. 計算機體系架構的經典書,學編譯器必看系列,本章的大多數描述來自這本書
- Kuck, D., Y. Muraoka, and S. Chen, On the number of operations simultaneously executable in Fortran-like programs and their resulting speedup. IEEE Transactions on Computers, pp. 1293-1310, 1972.
- Bernstein, D. and M. Rodeh, Global instruction scheduling for super-scalar machines, PLDI, pp. 241-255, 1991.