技術文章 » 強化學習-學習筆記12 | Dueling Network

強化學習-學習筆記12 | Dueling Network

2022-07-09 15:00:18

這是價值學習高階技巧第三篇，前兩篇主要是針對 TD 演演算法的改進，而Dueling Network 對 DQN 的結構進行改進，能夠大幅度改進DQN的效果。

Dueling Network 的應用範圍不限於 DQN，本文只介紹其在 DQN上的應用。

12. Dueling Network

12.1 優勢函數

Advantage Function.

回顧一些基礎概念：

  1. 折扣回報：

    \(U_t = R_t + \gamma \cdot R_{t+1} + \gamma^2R+...\)

  2. 動作價值函數：

    \(Q_\pi(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]\)

    消去了未來的狀態 和 動作，只依賴於當前動作和狀態，以及策略函數 \(\pi\)。

  3. 狀態價值函數：

    \(V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A)]\)

    只跟策略函數 \(\pi\) 和當前狀態 \(s_t\) 有關。

  4. 最優動作價值函數

    \(Q^*(s,a)=\mathop{max}\limits_{\pi}Q_\pi(s,a)\)

    只依賴於 s,a，不依賴策略函數。

  5. 最優狀態價值函數

    \(V^*(s)=\mathop{max}\limits_{a}V_\pi(S)\)

    只依賴 S。

下面就是這次的主角之一：

  • Optimal Advantage function 優勢函數：

    \(A^*(s,a)=Q^*(s,a)-V^*(s)\)

    V* 作為 baseline ，優勢函數的意思是動作 a 相對 V* 的優勢，A*越好，那麼優勢就越大。

下面介紹一個優勢函數有關的定理：

定理一：\(V^*(s)=\mathop{max}\limits_a Q^*(s,a)\)

這一點從上面的回顧不難看出，求得最優的路徑不同，但是相等。

上面提到了優勢函數的定義：\(A^*(s,a)=Q^*(s,a)-V^*(s)\)

同時對左右求最大值：\(\mathop{max}\limits_{a}A^*(s,a)=\mathop{max} \limits_{a}Q^*(s,a)-V^*(s)\)，而等式右側正是上面定理，所以右側==0；因此優勢函數關於a的最大值=0，即：

\(\mathop{max}\limits_{a}A^*(s,a)=0\)

我們把這個 0 值式子加到定義上，進行簡單變形：

定理二：\(Q^*(s,a)=V^*(s)+A^*(s,a)-\mathop{max}\limits_{a}A^*(s,a)\)

Dueling Network 就是由定理二得到的。

12.2 Dueling Network 原理

此前 DQN 用\(Q(s,a;w)\) 來近似 \(D^*(s,a)\) ，結構如下：

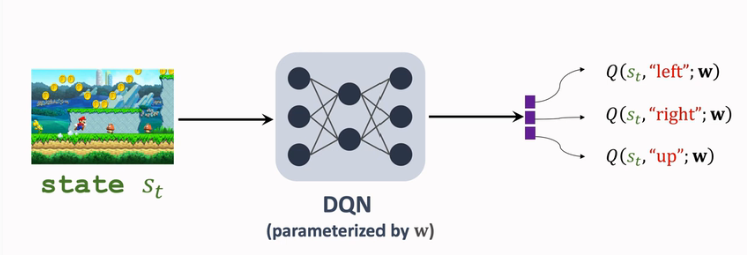
而 Dueling Network 對 DQN 的結構改進原理是：

  • 我們對於DQN的改進思路就是基於上面的定理2：\(Q^*(s,a)=V^*(s)+A^*(s,a)-\mathop{max}\limits_{a}A^*(s,a)\)

    • 分別用神經網路 V 和 A 近似 V-star 和 A-star
    • 即：\(Q(s,a;w^A,w^V)=V(s;w^V)+A(s,a;w^A)-\mathop{max}\limits_{a}A(s,a;w^A)\)
    • 這樣也完成了對於 Q-star 的近似，與 DQN 的功能相同。

  • 首先需要用一個神經網路 \(V(s;w^V)\) 來近似 \(V^*(s)\)：

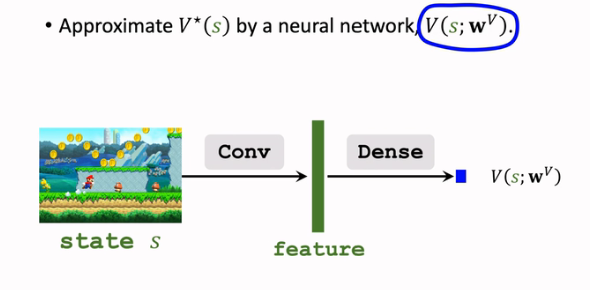
注意這裡的輸出是一個實數，是對狀態的打分，而非向量；

  • 用另一個神經網路\(A(s,a;w^A)\) 對\(A^*(s,a)\) 進行近似:

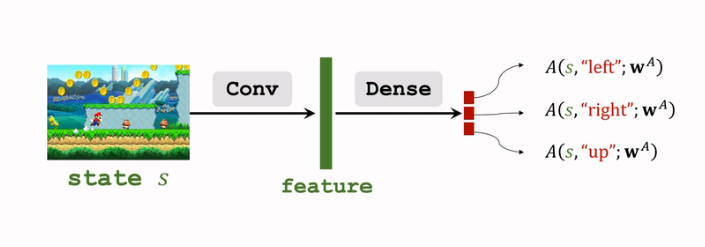
這個網路和上面的網路 \(V\) 結構有一定的相像，可以共用折積層的引數;

後續為了方便，令 \(w=(w^A,w^V)\)，即：

\[Q(s,a;w)=V(s;w^V)+A(s,a;w^A)-\mathop{max}\limits_{a}A(s,a;w^A) \]

現在 左側 與 DQN 的表示就一致了。下面搭建Dueling Network，就是上面 V 和 A 的拼接與計算：

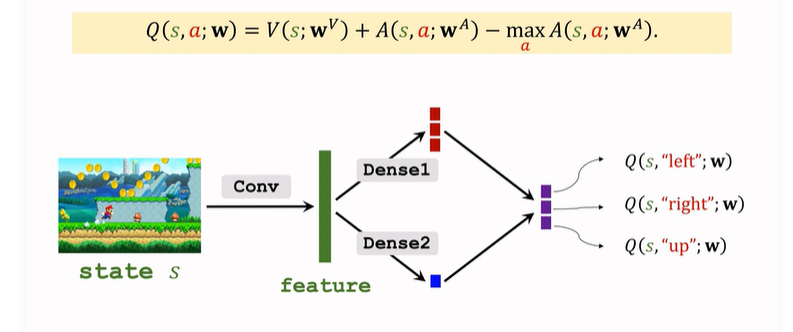
  • 輸入 狀態 s，V 和 A 共用一些 折積層，得到特徵向量；
  • 分別通過不同的全連線層，A輸出向量，V輸出實數；
  • 通過上面的式子運算輸出最終結果，是對所有動作的打分；

可見Dueling Network 的輸入 和 輸出 和 DQN 完全一樣，功能也完全一樣；但是內部的結構不同，Dueling Network 的結構更好，所以表現要比 DQN好；

注意，Dueling Network 和 DQN 都是對 最優動作價值函數 的近似。

12.3 訓練 Dueling Network

接下來訓練引數 \(w=(w^A,w^v)\)，採用與 DQN 相同的思路，也就是採用 TD演演算法訓練 Dueling Network。

之前介紹的 TD演演算法 的三種優化方法：

  1. 經驗回放 / 優先經驗回放
  2. Double DQN
  3. M-step TD target

都可以用在 訓練 Dueling Network 上。

12.4 數學原理與不唯一性

之前推導 Dueling Network 原理的時候，有如下兩個式子：

  • \(Q^*(s,a)=V^*(s)+A^*(s,a)\)
  • \(Q^*(s,a)=V^*(s)+A^*(s,a)-\mathop{max}\limits_{a}A^*(s,a)\)

我們為什麼一定要用等式 2 而不是等式 1 呢？也就是為什麼要加上一個 值為 0 的 \(\mathop{max}\limits_{a}A^*(s,a)\)？

  • 這是因為 等式1 有一個問題。

  • 即我們無法通過學習 Q-star 來 唯一確定 V-star 和 A-star，即對於求得的 Q-star 值，可以分解成無陣列 V-star 和 A-star。

  • \(Q(s,a;w^A,w^V)=V(s;w^V)+A(s,a;w^A)-\mathop{max}\limits_{a}A(s,a;w^A)\)

  • 我們是對 左側Q 來訓練整個 Dueling Network 的。如果 V 網路 向上波動 和 A 網路向下波動幅度相同，那麼 Dueling Network 的輸出完全相同，但是V-A兩個網路都發生了波動，訓練不好。

  • 而加上最大化這一項就能避免不唯一性；即如果 V-star 向上波動10，A-star 向下波動10，那麼整個式子的值會發生改變

    因為max項隨著A-star 的變化 也減少了10，總體上升了10

在上面的數學推導中，我們使用的是 \(\max \limits_{a}A(s,a;w^A)\)來近似最大項\(\max\limits_{a}A(s,a)\)，而在實際應用中，用 \(\mathop{mean}\limits_{a}A(S,a;w^A)\)來近似效果更好；這種替換沒有理論依據，但是實際效果好。

x. 參考教學