程式設計師的數學思維：如何推導矩形面積

矩形面積

小學課上我們就學過矩形的面積等於長乘以寬。

但活了幾十年，你有沒有想過：矩形面積為啥等於長乘以寬？

或者說先人們為何將矩形的面積定義為長乘以寬？

（繼續之前，請先忘掉矩形面積等於長乘以寬這個「簡單」的知識）。

時光倒退幾千年，小林是個好奇心極強的農夫，某天閒來無事，端著一杯茶盯著自家一塊地，就像下面這形狀：

小林突然想搞清楚這塊地有多大。於是他用尺子量了量：

他發現這塊地長邊是 100 米，短邊是 50 米。小林分別給這兩個邊起了個名字：長（長邊）、寬（短邊）。

因而現在可以說這塊土地大小是長 100 寬 50。

但小林那該死的好奇心對這個結果並不滿意：它想知道這麼大的矩形所圍出來的區域（陰影部分）到底是多大——它想用一個數位來表達這個區域。

小林現在還不知道這個長 100 寬 50 的矩形區域到底如何用數位表示——但到目前為止，這不重要，重要的是先給它起個名字。

名字叫什麼都行，不過最好能直觀，比如區域、面積——不妨就叫面積吧。

另外小林想求解的是通用矩形的面積（而不是長 100 寬 50 的」這個「矩形），所以他決定用一些符號來通用地表示矩形的長和寬。不妨用 l（或者別的什麼符號都行）代表長，用 w 代表寬。

現在問題變成：求長 l 寬 w 的矩形的面積是多少？

答案是：不知道！

到目前為止，小林的腦袋裡的數學知識只有數位（自然數）、加、減和乘——面對這個陌生的」面積「概念，他一籌莫展。

人類有個天生的」優點「：善於自欺欺人。

我們不知道矩形面積是多少對不對？但可以假裝知道啊！

就像我們給矩形的長和寬符號化一樣，我們也可以給面積一個符號。

給什麼符號無所謂，X、Y、面、# 都行——不妨管它叫 S 吧（雖然後人總是從語言歷史的角度來考證符號的含義，但實際上給它什麼符號真的無所謂）。

現在小林好像多了一點知識：知道了長 l 寬 w 的矩形的面積是 S。

但實際上他又什麼都不知道——其實不然，他憑經驗感覺這個 S 和 l、w 有關係（有什麼關係還不清楚）。

為了表示這個」重大「的發現（S、l、w 之間存在某種關係），小林給出如下縮寫：S(l,w)。

（用其它任何縮寫都行，比如 S[l,w]、l,w -> S 等等，我們之所以用 S(l,w) 純屬個人偏好。）

S(l,w) 和 S 這兩種表達其實是一個意思，都是表示矩形的面積，只不過前者多了進一步的含義：矩形的面積和長 l、寬 w 多少存在某種關係。

接下來小林自然就會想：它們到底存在什麼關係呢？

他低頭思考了半天不得其解。

就在小林快放棄的時候，他的眼角餘光瞟向那一畝三分地，小林想：既然它們存在關係，那我就試著改變長和寬，看看面積會發生什麼變化？

首先，他把長 l 加倍：

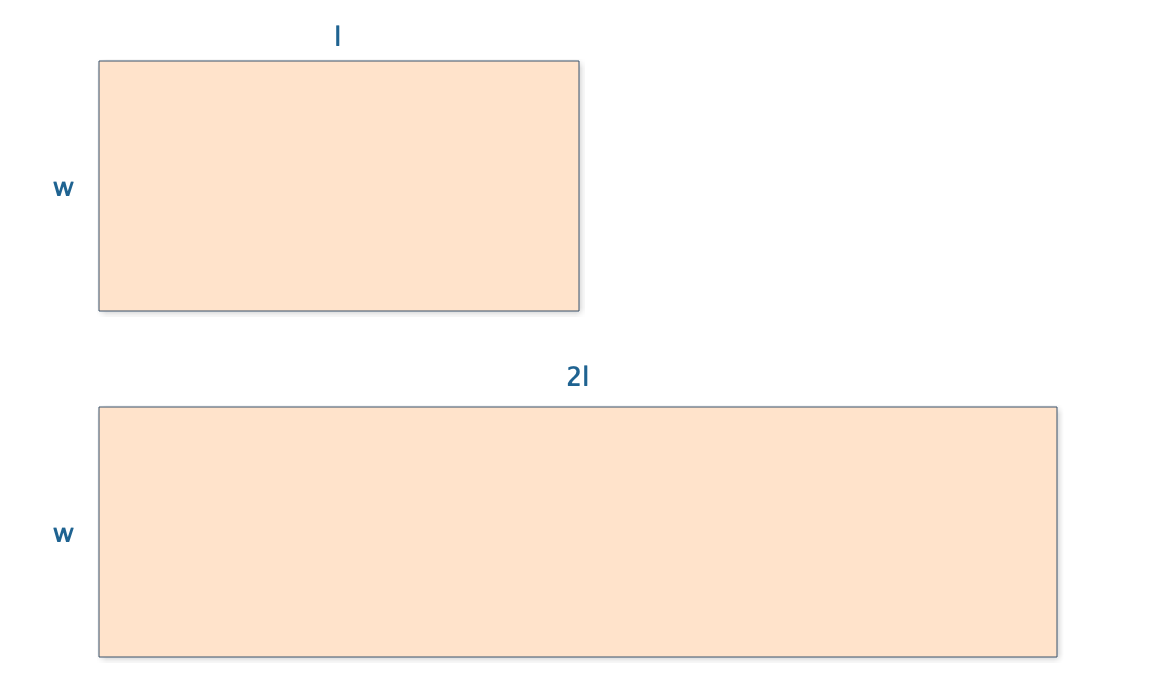
小林發現，長加倍後，面積也明顯加倍了，於是得到如下等式：

S(2l,w) = 2S(l,w)

有點意思！

接下來將長保持不變，寬加倍試試：

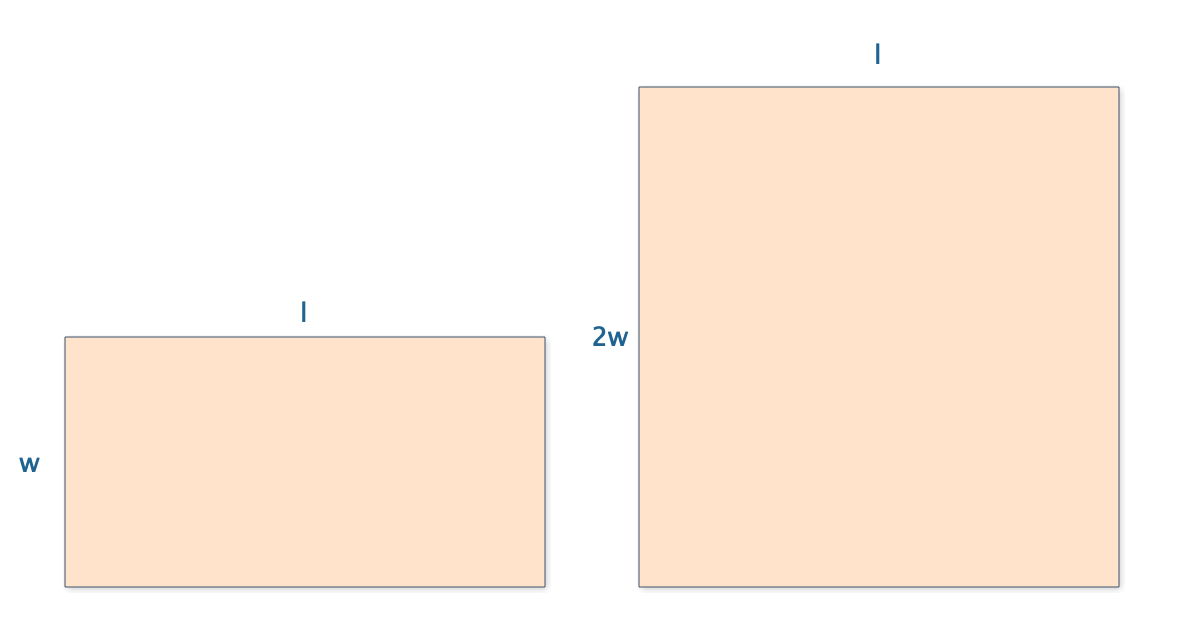
面積同樣加倍了：

S(l,2w) = 2S(l,w)

小林覺得看到希望了！

於是他拿起樹枝在地上畫起來——小林發現，無論長、寬增加（或減少）多少倍，面積都跟著增加（或減少）一樣的倍數。於是小林寫下了如下式子：

S(#l,w) = #S(l,w)

S(l,#w) = #S(l,w)

# 表示任意數。上面的式子是說：我們可以將矩形的長拆分成兩個任意數（#、l）的乘積，然後將其中一個數從括號裡面拿出來。對於寬也是如此。

接下來就要發揮人類的推理能力了。

S(l,w) 可以寫成 S(l*1,w)。按照上面的式子，我們可以將 l 從括號裡面拿出來得到：

S(l,w) = S(l*1,w) = l*S(1,w)

我們再對 w 做同樣的處理，得到：

S(l,w) = S(l*1,w) = l*S(1,w) = l*S(1,w*1) = l*w*S(1,1)

也就是說：S(l,w) = l*w*S(1,1)。

至此小林得到結論：長 l 寬 w 的矩形的面積是 長 1 寬 1 的矩形的面積的 l*w 倍。

小林並沒有得到一個絕對數，而是得到了一個相對於 長 1 寬 1 的長（正）方形的面積的倍數。

因為這個長 1 寬 1 的矩形面積總是固定的，所以我們並不需要關心它的面積絕對值到底是多少，我們可以把它人為地定義為 1，那麼長 l 寬 w 的矩形的面積就是 l*w。

這個思想很重要：我們在現實世界中理所當然地認為是絕對值的（比如這裡的面積），其實本質上是相對值。

比如 3 米到底是多長？它取決於 1 米有多長。

1 分鐘有多久？它取決於 1 秒有多久。

這些作為度量參照的，我們稱之為單位。

最底層的單位是人為定義的，而且在人類的不同歷史時期可能有不同的定義。比如中國古代的 1 斤跟現代的 1 斤在重量上並不相等，但它並不妨礙兩個時代人的日常使用。

怎麼做的？

在一般人看來，數學是人類最嚴謹的學科，就好像是神靈賜予人類的先驗禮物。

數學是嚴謹不假，但數學的基礎並不是先驗的，而是源自人類生活的經驗。

雖然數學中充斥著大量的公理、證明啥的，但數學最底層卻是一些」簡單「的公設（公理。比如平面幾何學中的五大公設）。小學老師告訴我們：所謂公理，是不需要證明的（不證自明）。這個所謂的」不證自明「，說白了就是憑經驗。

不但數學中最基本的公理憑經驗，數學中的很多求證過程也是憑經驗——雖然聽起來不可思議。

我們回頭看看矩形面積的推導過程：

一開始我們只是好奇心作怪，想知道如何用數來表示這麼一塊矩形區域（定義問題）。

我們發現自己不知道怎麼求解它，沒辦法只能給它個代號（符號化）。

另外我們發現矩形有兩個屬性：長和寬（引數化）。

經驗告訴我們，矩形面積跟矩形的長和寬存在某種關係（關聯）。

於是我們根據經驗試圖去尋找它們之間到底存在哪些關係（找規律）。

經過窮舉，我們得到了幾個很有意思的等式。

再經過一番思考和觀察，我們發現這幾個等式可以泛化成一般等式（就是裡面的具體數值可以變數化）。（關係泛化）

面對一般化的等式，我們利用已有知識（如 w = w * 1，即一個數乘以 1 等於它自身，這是根據乘法的定義得出的結論），最終推匯出我們想要的東西（基於既有知識的邏輯推理）

在整個過程中，經驗、觀察、實驗、符號化起到非常重要的作用。

關程式設計師何事？

這裡涉及到我們如何思考和解決問題。

當我們面臨一個陌生的（而且看起來很難的）問題時，本能反映是摸不著頭腦。

然後就開始抓瞎。

我們要做的是，在抓瞎之前冷靜一下，眼睛看看遠方，做幾次深呼吸，然後再多想幾次問題本身。

不要在還沒搞清楚問題是什麼之前就開始解決問題。

我們舉個字串編輯距離的例子。

問題：給定兩個字串 str1 和 str2，求 str1 至少需要經過多少次操作才能變成 str2。

你第一次遇到這個問題是什麼感受呢？反正我是一臉懵逼，狗咬刺蝟，無處下牙。

然後的感覺是：這個問題我好像沒怎麼弄明白？

所以要先分析問題本身。

什麼叫」經過多少次操作「？

想要知道經過多少次操作，起碼先要知道都有什麼樣的操作吧？

我們記得前面那位老農是面對著他的一畝三分地想問題——而我們現在面對的是兩個抽象的（符號）str1 和 str2。

所以接下來要將抽象的問題具象化。

我們不妨寫兩個具體的字串：

str1 = "abcd"

str2 = "acdb"

現在變成了具體的問題：怎樣通過最少的操作將字串"abcd"變成"acdb"？

這個問題其實分兩部分：

1. 怎樣的操作？
2. 最少的操作？

一個字串想變成另一個字串，它總要一個字元一個字元地處理吧（你不可能連看都不看某個字元一眼就能做出正確決定）。

所以」操作「這個概念就變成了」一個字元怎樣變成另一個字元「的問題。

我們就看第一個字元：str1 中的 a 如何變成 str2 中的 a？

想都不用想，它倆相等，不用做任何操作——不做任何操作本身就是一種操作型別。

然後我們看看第二個字元：str1 中的 b 如何變成 str2 中的 c？

它倆不一樣，所以必須做些行動才行。

一種方案是，將 b 替換成 c。

第二種方案是，直接將 b 刪除掉，讓它後面的字元來應對 c 這個字元。

第三種方案是，在 a 和 b 之間插入 c（將 b 挪到後面去）。

沒有其他方案了。

至此我們搞明白了所謂」操作「到底是什麼：啥也不做、替換、刪除、插入，一共四種。

然後我們再把那個恐怖的修飾語」最少的「加上去——你會發現此時頭又大了。

如果不限制」最少「，其實很好辦，最無腦的做法就是先把 str1 中的字元全刪掉，然後再一股腦把 str2 中的每個字元挨個插入即可，操作步數是 n + m（兩個字串長度之和）。

這個最無腦的解法雖然無用，但它揭示了該問題的最大操作步數是 n+m，所以如果你整出的解比它還大，那肯定不對了。

我們再回到上面的具體字串：怎樣通過最少的操作將字串"abcd"變成"acdb"？

我們一個一個嘗試。

其中一種方案是：第一個 a 保持不變，刪掉第二個 b，最後在 d 後面插入 b，操作步數是 2。

然後我們又人肉嘗試了其它方案，發現所有方案中最小的就是 2。

然而，問題好像並沒有什麼進展——我們仍然不知道如何求得最少步數（除了人肉）。

如果我們的思路一直停留在具象的具體問題上，便不太可能得到問題的解。

人類區別於其他動物的地方在於，人類能夠將具象的事物（現象）提升成抽象的符號，進而形成思維模型（這也正是數學的奧祕，現在你應該能夠理解數學家為啥那麼喜歡玩符號了）。

將問題具象化有助於我們深刻理解問題本身，現在是時候讓思維從具象回到抽象層面了。

我們先對字串本身做抽象化表述。

字串就是字元序列，它的本質就是集合（外加了個限制：順序相關，即裡面的字元有特定順序）。

所以問題變成：如何通過最少操作步數將長度為 n 的字元序列 \(\{x,y,z\cdots\}_n\) 轉換成長度為 m 的字元序列 \(\{x^\prime,y^\prime,z^\prime\cdots\}_m\)？

答案是：不知道！

那位農夫在求不出面積的時候做了個驚人的舉動：給它個符號！

我們也這麼辦。

我們假設 \(\{x,y,z\cdots\}_n\) -> \(\{x^\prime,y^\prime,z^\prime\cdots\}_m\) 的最小編輯距離是 N（管它怎麼求的）。

跟農夫將 S 換成 S(l,w) 以體現面積和邊長的關係一樣，我們也將引數放進去：

N(str1, str2)

這個組合符號是說：它能算出字串 str1轉換為 str2 的最少操作步數（最小編輯距離）。

至於它怎麼算的，我們暫時不關心。

這玩意是不是像極了程式設計中的介面？

作為程式設計師，你可能覺得這個 N 太醜了，那我們換個」人性化「點的名字：shortestEditDist(str1, str2)。

然後——我們盯著這奇怪的符號思考了半天，一籌莫展！

符號本身並不能告訴我們更多，我們必須開動推理的馬達去加工符號。

對於集合型別問題，我們常用的一種思維模式是：看能否通過子集的解推出父集的解。

具體地，對於」串「類的問題，假如我們已經知道某個子串的解，看能否通過這個子串推出某個父串的解。

作這種解題假設的依據是：子串和父串具有相同的模式。

假設我們已經知道了 str1 中子串 [0,i] 轉換成 str2 中子串 [0,j] 的最少操作步數是 M（先不管怎麼算出來的），能不能求出 str1 中子串 [0,i+1] 轉換成 str2 中子串 [0,j+1] 的最少操作步數？

可以吧？它其實就是在原來的基礎上各加了一個字元——一個字元我們是能搞定的。

有了這個發現，我們先修正一下我們的組合符號（函數宣告），將其改成：

shortestEditDist(str1, str2, i, j)

意思變成：我能求子串 str1[0,i] -> str2[0,j] 的最小編輯距離 M（管它怎麼求呢，先放出大話再說）。

現在的問題變成：如何通過子串 str1[0,i] -> str2[0,j] 的最小編輯距離 M 推導子串 str1[0,i+1] -> str2[0,j+1] 的編輯距離？

我們假設 str1 的第 i+1 位的字元是 x（表示未知的某個字元），str2 的 第 j+1 位的字元是 y（另一個未知字元），如果 x 等於 y，則不用做任何操作，即最少操作步數仍然是 M；如果 x 不等於 y，則必須通過替換、刪除、插入中的一種操作才能實現轉換，此時最少操作步數是 M+1。

問題是，當 x 不等於 y 的時候，到底採用三種中的哪種操作呢？

三種操作的區別在於對後面字元的影響：

• 採用刪除方案，則下一步要處理的是 str1 的 i+2 位置的字元和 str2 的 j+1 位置的字元（刪除的意思是試圖用源字串下一個位置的字元來解決目標字串當前位置的字元）；
• 採用插入方案，下一步要處理的是 str1 的 i+1 位置的字元和 str2 的 j+2 位置的字元（插入的意思是直接在當前位置新生成目標字串的字元，將原本該位置的字元留下來用以解決目標字串的下一個字元）；
• 採用替換方案：則是一對一抵消，下一步處理的是 str1 的 i+2 位置字元和 str2 的 j+2 位置的字元；

事實是：我們根本不知道哪種方案能使整體操作步數最少——除非一個一個嘗試。

那就一個一個試吧！

我們寫一下程式碼：

// 我能算出子串 str1[0,i] 轉換為 str2[0,j] 的最小編輯距離，其中 0 <= i < n，0 <= j < m
func shortestEditDist(str1, str2 string, i, j int) int {
    // 還沒想好怎麼實現...
}

// 求 str1 轉成 str2 的最小編輯距離
func EditDistance(str1, str2 string) int {
    // 既然你做了那樣的宣告，我就這樣用
    // 算不出來唯你是問！
    return shortestEditDist(str1, str2, len(str1)-1, len(str2)-1);
}

既然吹了牛，終究還是要兌現它。

現在我們想想 shortestEditDist 具體怎麼實現。

根據前面的思路，我們可以用 shortestEditDist(str1, str2, i-1, j-1) 來求解 shortestEditDist(str1, str2, i, j)。

// 我能算出子串 str1[0,i] 轉換為 str2[0,j] 的最小編輯距離，其中 0 <= i < n，0 <= j < m
// 實現方式：用 shortestEditDist(str1, str2, i-1, j-1) 來求解  shortestEditDist(str1, str2, i, j)
// 也就是暴力遞迴
func shortestEditDist(str1, str2 string, i, j int) int {
    // 考慮具體情況之前，先考慮遞迴函數的終止條件
    if i == -1 && j == -1 {
        // 兩個都是空串，無需做任何處理
	return 0
    }

    if j == -1 {
        // str2 的子串是空串，str1 的子串[0,i] 只能採用刪除操作才能轉為 str2 的子串
        return i + 1
    }

    if i == -1 {
        // str1 的子串是空串，此時只能採用插入操作才能轉為 str2 的子串
	return j + 1
    }

    // 一般情況，根據我們前面的討論，有四種情況

    // 情況1：當前兩個字元相同
    if str1[i] == str2[j] {
        // 兩個字元相同，先將 str1[0,i-1] 轉成 str2[j-1]，然後本步驟啥也不做
        return shortestEditDist(str1, str2, i-1, j-1)
    }
	
    // 情況2：兩個字元不同，有三種情況
    // 因為我們不知道本步驟到底採用什麼方案才會讓整體操作步數最少，所以只能都嘗試一遍，然後取最小值
    // 注意：我們在前面是從左往右思考問題的（往後推），而這裡遞迴求解的方向是相反的（往前推），思維要稍微轉換下

    // 選擇1：先用 str1[0,i-1] 轉換出 str2[0,j]，再刪除 str1[i]
    c1 := shortestEditDist(str1, str2, i-1, j) + 1

    // 選擇2：先用 str1[0,i] 轉換出 str2[0,j-1]，再在後面插入 str2[j] 字元
    c2 := shortestEditDist(str1, str2, i, j-1) + 1

    // 選擇3：先用 str1[0,i-1] 轉換出 str2[0,j-1]，再將 str1[i] 替換成 str2[j]
    c3 := shortestEditDist(str1, str2, i - 1, j - 1) + 1

    // 取三種情況代價最小的
    return minInt(c1, c2, c3)
}

如此就求出來了。

有研究過最小編輯距離的同學可能知道最小編輯距離可以通過動態規劃解決，效能更高。
本文之所以使用暴力遞迴，因為一方面它和動態規劃的思路本質是一樣的，都是遞推（或說歸納法）解題。會動態規劃的同學很容易將暴力遞迴改造成動態規劃，而不會的，看遞迴寫法要比看動態規劃寫法直觀明白得多。

初識遞迴思想的同學覺得這玩意不可思議，咋在不知不覺中就把結果求出來了呢？

其實它就是我們在高中學的那個強大而陌生的數學歸納法，它要求問題具備三個特性：

1. 一個集合和它的任意子集具有相同的模式；
2. 可以通過子集 \(S_n\) 的解求 \(S_{n+1}\) 的解；
3. 能夠知道初始值（如 n=0）的解；

它的思想很簡單：既然能夠通過 \(S_n\) 的解求 \(S_{n+1}\) 的解，而我們又知道 \(S_0\) 的解，那一定能知道 \(S_1\) 的解，進而知道 \(S_2\) ......

有一點需要注意的是，我們在前面推導（遞推）的時候，是通過 \(S_n\) 的解推導 \(S_{n+1}\) 的解（邏輯上是先考慮 \(S_n\) ），而在寫遞迴函數的時候恰恰是反過來的：我們是先考慮 \(S_{n+1}\)，在處理過程中發現需要藉助 \(S_{n}\) 來求解。而寫在遞迴函數開頭的函數終止條件恰恰就是遞推（或說數學歸納法）中的初始值。

總結

雖然推導矩形面積和求解字串最小編輯距離在邏輯上存在很大差別，但在思維模式上存在很多相似性：

1. 先定義清楚問題（什麼是面積；什麼是編輯距離）；
2. 用具體範例深入理解和挖掘問題（50*100 的矩形；"abcd" 和 "acdb" 兩個字串）；
3. 將求解物件引數化（矩形的長 l、寬 w；最小編輯距離中的 i、j）；
4. 將未知解符號化（面積 S；最小編輯距離 N）；
5. 將符號和引數組合成新的複合符號（函數。比如面積中的 S(l,w)；編輯距離中的 N(str1,str2,i,j)），給問題和解建立初步的關係；
6. 通過觀察、試驗，探求不同引數對解的影響（矩形邊長加倍讓面積加倍；可以用 str1[n-1] -> str2[m-1] 的解求 str1[n] -> str2[n] 的解）；
7. 泛化第 6 步，得出最終解；