強化學習-學習筆記9 | Multi-Step-TD-Target

這篇筆記依然屬於TD演演算法的範疇。Multi-Step-TD-Target 是對 TD演演算法的改進。

9. Multi-Step-TD-Target

Sarsa
- 訓練動作價值函數 \(Q_\pi(s,a)\)；
- TD Target 是 \(y_t = r_t + \gamma\cdot Q_\pi(s_{t+1},a_{t+1})\)
Q-Learning
- 訓練最優動作價值函數 Q-star；
- TD Target 是 \(y_t = r_t +\gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},a)\)
注意，兩種演演算法的 TD Target 的 r 部分都只有一個獎勵 \(r_t\)
如果用多個獎勵，那麼 RL 的效果會更好；Multi-Step-TD-Target就是基於這種考慮提出的。

在第一篇強化學習的基礎概念篇中，就提到過，agent 會觀測到以下這個軌跡：

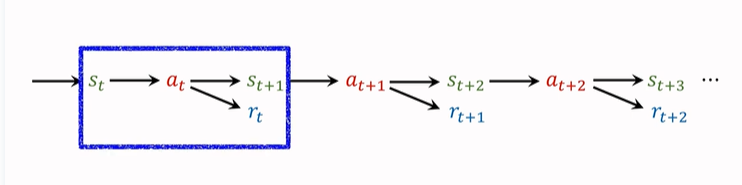
我們之前只使用一個 transition 來記錄動作、獎勵，並且更新 TD-Target。一個 transition 包括\((s_t,a_t,s_{t+1},r_t)\)，只有一個獎勵 \(r_t\)。（如上圖藍框所示）。

這樣算出來的 TD Target 就是 One Step TD Target。

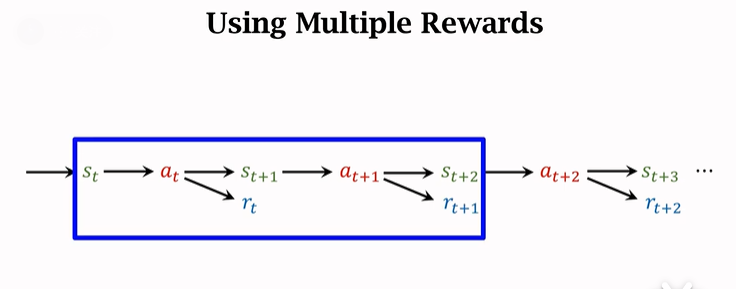
其實我們也可以一次使用多個 transition 中的獎勵，得到的 TD Target 就是 Multi-Step-TD-Target。如下圖藍框選擇了兩個 transition，同理接下來可以選後兩個 transition 。

Multi-Step Return.

折扣回報公式為：\(U_t=R_t+\gamma\cdot{U_{t+1}}\)；

這個式子建立了 t 時刻和 t+1 時刻的 U 的關係，為了得到多步折扣回報，我們遞迴使用這個式子：

\(U_t=R_t+\gamma\cdot{U_{t+1}}\\=R_t+\gamma\cdot(R_{t+1}+\gamma\cdot{U_{t+2}})\\=R_t+\gamma\cdot{R_{t+1}}+\gamma^2\cdot{U_{t+2}}\)

這樣，我們就可以包含兩個獎勵，同理我們可以有三個獎勵......遞迴下去，包含 m個獎勵為：

\(U_t=\sum_{i=0}^{m-1}\gamma^i\cdot{R_{t+i}}+\gamma^m\cdot{U_{t+m}}\)

即：回報 \(U_t\) 等於 m 個獎勵的加權和，再加上 \(\gamma^m\cdot{U_{t+m}}\)，後面這一項稱為 多步回報。

現在我們推出了多步的 \(U_t\) 的公式，進一步可以推出多步 \(y_t\) 的公式，即分別對等式兩側求期望，使隨機變數具體化：

Sarsa 的 m-step TD target：

\(y_t=∑_{i=0}^{m−1}\gamma^i\cdot r_{t+i}+\gamma^m\cdot{Q_\pi}(s_{t+m},a_{t+m})\)

注意：m=1 時，就是之前我們熟知的標準 TD Target。

多步的 TD Target 效果要比單步好。
Q-Learning 的 m-step TD target：

\(y_t = \sum_{i=0}^{m-1}\gamma^i{r_{t+i}}+\gamma^m\cdot\mathop{max}\limits_{a} Q^*({s_{t+m}},a)\)

同樣，m=1時，就是之前的TD Target。

單步 TD Target 中，只使用一個獎勵 \(r_t\)；
如果用多步TD Target，則會使用多個獎勵：\(r_t,r_{t+1},...,r_{t+m-1}\)

聯想一下第二篇價值學習的旅途的例子，如果真實走過的路程佔比越高，不考慮「成本」的情況下，對於旅程花費時間的估計可靠性會更高。
m 是一個超引數，需要手動調整，如果調的合適，效果會好很多。