論文資訊

論文標題：Rethinking the Setting of Semi-supervised Learning on Graphs
論文作者：Ziang Li, Ming Ding, Weikai Li, Zihan Wang, Ziyu Zeng, Yukuo Cen, Jie Tang
論文來源：2022, arXiv
論文地址：download 
論文程式碼：download 

1 Introduction

　　本文主要研究半監督GNNs 模型存在的超調現象（over-tuning phenomenon），並提出了一種公平的模型對比架構。

2 The Risk of Over-tuning of Semi-supervised Learning on Graphs

2.1 Semi-Supervised Learning on Graphs

　　常用的三個資料集：

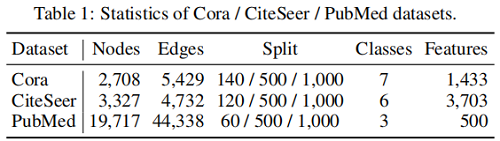
2.2 An Analysis of Over-tuning in Current GNNs

　　超調現象（over-tuning phenomenon）普遍存在GNNs中，即 GNN 模型的超引數過分擬合驗證集。

　　本文測試了5種代表性的 GNNs 框架（GCN, GAT, APPNP, GDC-GCN, ADC）在 Cora 資料集上不同驗證集尺寸上的準確率對比。本文采用網格搜尋為每個模型選擇最優的超引數。將驗證集的大小從 100 到 500。對於每個驗證集，在使用最佳搜尋的超引數訓練模型後，報告測試集上的結果。結果如 Figure1 所示。

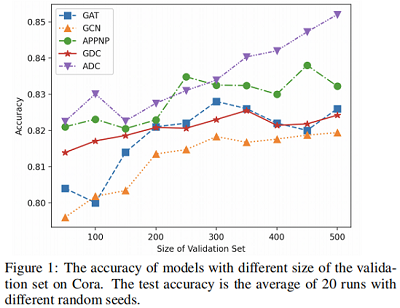
　　Figure 1 顯示，GNN模型使用更大的驗證集的效能通常更好。由於驗證集只能通過超引數來影響模型，因此我們可以得出結論，該模型可以利用超引數從驗證標籤中獲益。如果我們將驗證集的大小從 100 增加到 500，準確率提高高達 1%∼3% ，這足以表明過度調優已經存在。

2.3 ValidUtil: Exploring the Limits of Over-tuning

　　通常不能將驗證集加入到訓練集中，這是被認為是一種資料洩露。本文提出的 ValidUtil 如：

　　結果發現：只有當 $\hat{y}_{i}=y_{i}$ 時，模型才能達到最好的結果。Figure 2 表明了  hyper-parameters 對實驗的影響：

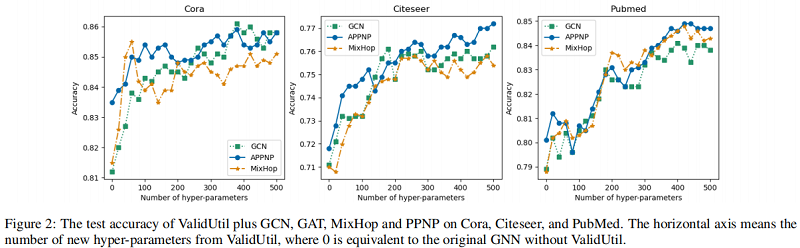
　　我們發現，即使從ValidUtil中只有20個∼60個超引數，也可以給某些模型帶來效能上的飛躍。當我們為驗證集中的所有500個節點新增超引數時，PPNP可以比 Table 2 中的SOTA 方法。

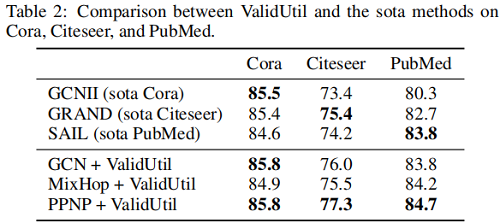
　　備註：雖然ValidUtil純粹通過使用驗證標籤來工作，但它在當前設定下是完全有效的。如果我們將GNN+ValidUtil視為一個黑盒模型，那麼訓練過程是相當正常的。ValidUtil實際上使用標籤的效率很低，因為每個超引數只能學習一個節點的資訊——但這足以驗證我們的假設。當前設定無法阻止驗證標籤在超引數調優期間「洩漏」。我們認為有一些更有效的方法來定義有影響的超引數。這些超引數可能與特徵或模型結構糾纏在一起，它們可以從多個驗證標籤中獲取資訊。根據 Figure 1，這種有影響的超引數可能已經存在於一些模型中，不易檢測到。因此，迫切需要構建一個新的圖上的半監督學習基準，以避免過度調優和公平、穩健地比較GNN模型。

3 IGB: An Independent and Identically Distributed Graph Benchmark

3.1 Overview 

　　新基準測試的兩個目標：避免過度調優和更健壯。

　　為避免過度調優，本文將節點分為標記節點和未標記節點。可以採用任何方式來學習標記資料集的最佳模型，並評估未標記集（測試集）上的效能。若需要搜尋超引數，可以將一部分標記資料集當成驗證集。由於驗證標籤已經暴露出來，因此消除了過度調優的問題。這種設定更接近真實場景，能夠在具有不同超引數的模型之間進行公平比較。為了輕鬆地將 GNN 遷移到這個新的設定中，我們將在第3.2節中引入一個簡單而強大的方法來建立驗證集。

　　本文期望在不同的隨機種子下，模型的效能是穩定的。機器學習中報告效能的常用方法是：重複測試和報告平均效能。所以本文期望在多個 i.i.d 圖上測試模型的效能，這多個  i.i.d 圖 是取樣得到的。

• 1. Divide the labeled set into training and validation sets.
• 2. Find the best hyper-parameters using grid search on the training and validation sets from the first step.
• 3. Train the model with the best hyper-parameters on the full labeled nodes.
• 4. Test the performance of the model from the third step on the unlabeled (test) sets.
• 5. Repeat the above steps on each graph in a dataset and report the average accuracy

　　前兩步旨在找到GNN模型的最佳超引數。我們認為該方法適用於許多GNN模型獲得滿意的超引數。如果有其他合理的方法來確定帶標記集的最佳超引數，他們也將被鼓勵替換這個管道中的前兩個步驟。通過這種方式，可以通過在第三步直接公開驗證集中的所有標籤資訊來避免過度調優。

3.3 Datasets

 　　IGB由四個資料集組成：Aminer，Facebook，Nell，Flickr。每個資料集包含100個無向連通圖，根據第3.4節中的隨機遊動方法從原始的大圖中取樣。我們還報告了一對取樣圖的平均節點重疊率，即公共節點與節點總大小的比率。覆蓋率定義為100個取樣圖與原始大圖的並集之比。首選低重疊率和高覆蓋率。資料集的統計資料見表3。

3.4 Sampling Algorithm

　　使子圖的節點標籤分佈與原始圖相似的最簡單的方法是頂點抽樣。然而，它並不符合我們的期望，因為它生成了不連線的子圖。為獲得接近 i.i.d. 子圖的基準，我們必須仔細設計抽樣策略和原則。具體來說，我們期望抽樣策略具有以下特性：

• 1. The sampled subgraph is a connected graph.
• 2. The distribution of the subgraph’s node labels is close to that of the original graph.
• 3. The distribution of the subgraph’s edge categories (edge category is defined by the combination of its two endpoints’ labels) is close to that of the original graph.

　　首先，隨機遊走很好的滿足第一點，我們從節點 $u=n_0$開始取樣，通過轉換的可能性可以選擇以下節點：

　　　　$P_{u, v}=\left\{\begin{array}{ll}\frac{1}{d_{u}}, & \text { if }(u, v) \in E \\0, & \text { otherwise }\end{array}\right.$

　　其中，$P_{u, v}$ 是從 $u$ 到 $v$ 的轉移概率，$d_{u}$ 代表著節點 $u$ 的度。

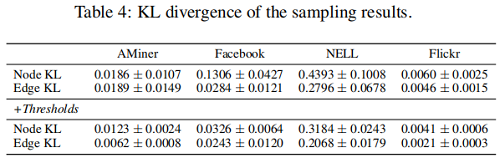
　　我們拒絕採用類似抽樣的方法，以保證第二個和第三個性質。在這裡，我們引入了 KL散度 作為一個度量來度量兩個不同分佈之間的差異。為了得到節點標籤分佈(「Node KL」)和邊緣類別分佈(「Edge KL」)KL散度相對較低的子圖，我們設定了一個預定義的閾值來決定是否接受取樣子圖。新增閾值前後的結果比較如 Table 4 所示。

3.5 Benchmarking Results

　　在這四個資料集上的結果：

　　

3.6 The Stability of IGB

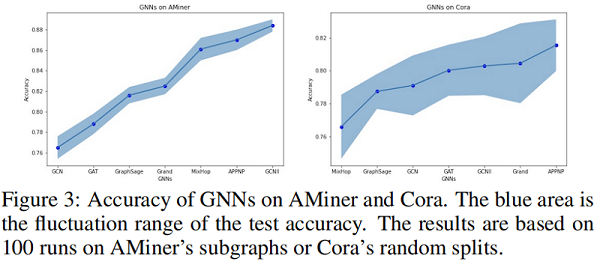
　　本文用兩種方法驗證了 IGB 的穩定性。首先，驗證它在不同的圖上評估模型時的穩定性，因為每個 IGB 資料集包含100個近 i.i.d. 圖。具體來說，我們比較了100個 AMiner子圖 和100 個Cora亂資料分割上的精度方差。Figure 3 結果表明，即使每個 AMiner 圖都使用了亂資料分割，對 IGB 的評估也比 Cora 風格更穩定。

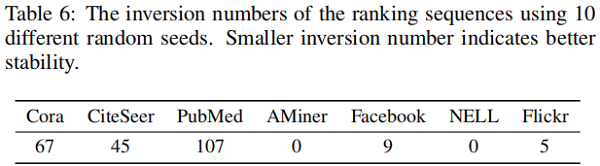
　　其次，關注IGB在評估具有不同隨機種子的模型時的穩定性。在一個穩定的基準測試中，不同模型的排名在改變隨機種子時不應該很容易地改變。為了驗證這一點，我們使用排名的 「inversion number」 作為度量。

4 Conclusion 

　　本文重新討論了圖上的半監督設定，並闡述了過度調優的問題，且通過 VallidUtil 驗證了他的意義。本文還提出了一個新的基準 IGB，一種更加穩定的評估管道。還提出一種基於 RW 取樣演演算法來提高評價的穩定性，本文希望通過IGB 能造福社會。

修改歷史

2022-07-07 建立文章

論文解讀目錄