Transformer演演算法完全解讀
2017年6月谷歌釋出論文《Attention is All You Need》,提出Transformer這一引燃機器學習領域的演演算法。數年過去,Transformer演演算法在計算機視覺、自然語言處理等眾多應用領域展現了極為驚豔的表現。
大家都是神經網路,為何你的腰椎間盤卻如此突出?
可以說,Transformer是完全基於自注意力機制的一個深度學習模型,且適用於並行化計算,導致它在精度和效能上都要高於之前流行的RNN迴圈神經網路。
在接下來的篇幅中,我們來詳細梳理Transformer演演算法各個細枝末節原理,並結合B站視訊教學:【Transformer為什麼比CNN好!】中的程式碼實現,展示Transformer的整個建模流程。
1 Transformer整體結構¶
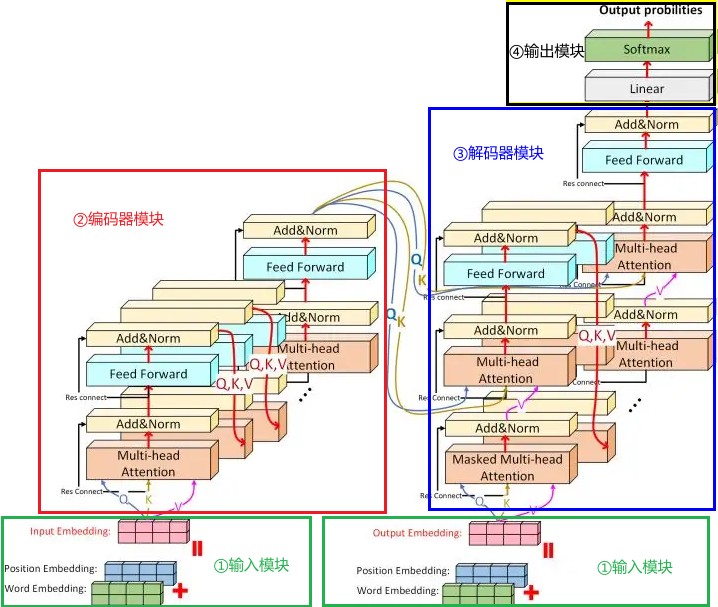
如圖1所示,是Transformer結構圖。乍一看,不明覺厲,頓時被勸退!別急!我們一步一步對圖中每一個元件進行歸類劃分,並以漢譯英模型為例結合資料流程進行說明。
從功能角度上,我將Transformer各個元件劃分到四個功能模組,對應於圖1中4中顏色框框選部分:輸入模組(綠色框框)、編碼器模組(紅色框框)、解碼器模組(藍色框框)、輸出模組(黑色框框)。
第一步,我們將詞庫中每一個詞(中文就是字了,為了更大眾化地表達,我們就稱之為詞吧)以及開始標誌轉化為嵌入詞向量,詞嵌入向量的維度為embedding dimension,一句話中總共的單詞長度為sequence length,因此可以得到一個sequence_length $\times$ embedding_dimension大小的矩陣,其中每一行代表的是一個詞。有了詞嵌入矩陣還不夠,還需要在矩陣中新增位置編碼,隨後將矩陣傳入編碼器模組。這一系列操作,就是輸入模組負責的功能。輸入模組有兩個部分,功能實現是一模一樣的,區別在於一個是對源資料進行編碼,也就是我們現在第一步中所做的操作,另一個是對目標資料進行編碼。
第二步,編碼器模組接收到輸入模組傳輸過來的矩陣後,要完成多頭注意力計算、規範化、前向傳播等等一系列操作,而且這些操作還不止進行一次(8次),最終將輸出結果傳入解碼器模組。編碼器模組是Transformer模型最為核心的部分,創新使用的多頭注意力機制是Transformer演演算法效能突出的關鍵。
第三步,接下來,輸出矩陣從編碼器傳到了解碼器模組,我們姑且稱這個矩陣為矩陣A吧。解碼器接收到矩陣A後,解碼器對應的輸入模組也開始工作,這個輸入模組會對目標資料進行詞嵌入、新增位置編碼等一些列操作,形成另一個矩陣,我也給它命一個名,叫矩陣B吧。矩陣B進入解碼器後,進行掩碼,再進行一次注意力計算,然後往前傳遞,與矩陣A「勝利會師」。會師後,兩者共同進行注意力計算,生成新的矩陣,並進行前向傳播和規範化。進行一系列類似操作後,將矩陣傳入輸出模組。從這裡可以看出,解碼器模組,是有兩個輸入的,一個來自於編碼器,一個來自於輸入模組對目標資料的編碼。
第四步,這是最後一步了,輸出模組對解碼器模組的輸出矩陣進行一次線性變換,然後通過softmax層轉換為概率分佈矩陣,矩陣中概率最大值對應的英文詞彙為這一次傳輸的輸出結果,即翻譯結果。
上述整體流程介紹,我們提到了許多概念和操作,例如詞嵌入、位置編碼、多頭注意力機制等等。接下來,我們再對各功能模組進行細分,對每一個元件進行說明,並對涉及到的概念,操作原理進行分析。
為保證後續各元件程式碼能夠正常執行,我們先匯入所有需要用到的模組:
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import math
import matplotlib.pyplot as plt
import numpy as np
import copy
import warnings
warnings.filterwarnings("ignore")
在自然語言處理模型中,需要將文字元號轉化為數學表示,即特徵向量。將詞彙表示成特徵向量的方法有多種:
- One-hot編碼
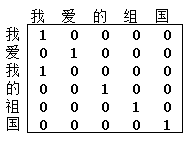
One-hot編碼使用一種常用的離散化特徵表示方法,在用於詞彙向量表示時,向量的列數為所有單詞的數量,只有對應的詞彙索引為1,其餘都為0。例如,「我愛我的祖國」這句話,總長為6,但只有5個不重複字元,用One-hot表示後為6$\times$5的矩陣,如圖1所示。但是但這種資料型別十分稀疏,即便使用很高的學習率,依然不能得到良好的學習效果。
- 數位表示
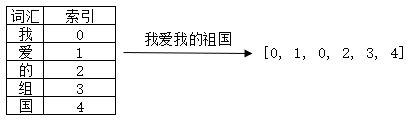
數位表示是指用整個文字型檔中出現的詞彙構建詞典,以詞彙在詞典中的索引來表示詞彙。所以,我認為,與其叫做「數位表示」,還不如叫「索引表示」。例如,「我愛我的祖國」這句話,就是我們整個語料庫,那麼整個語料庫有5個字元,假設我們構建詞典{'我':0, '愛':1, '的':2, '祖':3, '':4},「我愛我的祖國」這句話可以轉化為向量:[0, 1, 0, 2, 3, 4]。如圖3所示。這種方式存在的問題就是詞彙只是用一個單純且獨立的數位表示,難以表達出詞彙豐富的語意。
- word2vec
word2vec將給定詞表中的詞對映到低維稠密的向量空間中,在這個空間中語意相同的詞距離較近,例如,表示「國家」與「祖國」兩個詞彙的向量之間的距離要比「西紅柿」與「祖國」兩個詞彙對應向量的距離要小的多。 從這個角度上說,One-hot編碼以及數位表示方式更加側重於對詞彙字元本身的表示,而word2vec要側重於對詞彙語意的表示。這就解決了one-hot編碼所帶來的維度災難和語意缺失現象。然而,word2vec仍無法解決一詞多義 的表徵,例如,「我一邊用蘋果手機看電影,一併吃著蘋果」,這句話中出現兩個「蘋果」,但是在word2vec只會用一個詞向量來表示「蘋果」一詞,後續的bert很好的解決了這個問題。
本文重點不是介紹詞彙向量表示,不在例舉。假設我們已經完成了詞彙的向量表示,例如,我們使用「數位表示」的方式,將語料庫中所有文字轉化為了向量,那麼接下來,就要進行Embedding操作。為什麼需要進行Embedding呢?其實就是為了解決上述各種詞彙向量表示的不足:過於稀疏、低維向量空間不能表達語意、表達不了一次多義等。 經過Embedding後,詞彙轉化為指定維度的向量,且相似的語意詞彙在向量空間中距離更近。關於Embedding原理,可以閱讀這篇文章。
在Pytorch中,提供有專門的Embedding功能高層API,直接使用即可。
class Embedding(nn.Module):
# embedding層
def __init__(self, d_model, vocab):
# d_model: 詞嵌入的維度(轉換後獲得的詞向量的維度)
# vocab:詞表 的大小
super(Embedding, self).__init__()
# 定義Embedding層
self.lut = nn.Embedding(vocab, d_model)
# 將引數傳入類中
self.d_model = d_model
def forward(self, x):
# x:代表輸入進模型的文字通過詞彙對映後的數位張量
return self.lut(x) * math.sqrt(self.d_model) # 陳尚d_model的開根號是為了對最後結果進行一個縮放
我們嘗試使用這個Embedding類,對上文中「我愛我的祖國」這句文字數位表示後的向量[0, 1, 0, 2, 3, 4],進行Embedding。當然,因為此時的Embedding沒有經過任何訓練,初始化引數是完全隨機的,所以基本不存在什麼相似的語意表示:
x = Variable(torch.LongTensor([[0, 1, 0, 2, 3, 4]]))
emb = Embedding(4, 5) # 語料庫共有5個詞,每個詞轉化為3維向量表示
embr = emb(x)
print("embr:", embr)
print("shape:", embr.shape)
embr: tensor([[[-0.9873, 1.2457, 0.7959, 0.3183],
[-2.2986, 1.9885, 0.4855, -2.1126],
[-0.9873, 1.2457, 0.7959, 0.3183],
[ 0.8325, 2.1043, 0.4781, -2.9356],
[-1.2173, 2.6160, -0.6300, -2.0037],
[-0.7444, 2.6920, 4.4916, -2.0474]]], grad_fn=<MulBackward0>)
shape: torch.Size([1, 6, 4])
最終輸出張量的shape為什麼為[1, 6, 4]呢?[1, 6, 4]分別對應[batch size, sequence length, embedding dimension],也就是批次大小、每個句子長度(每個句子詞的數量)、詞嵌入維度(每個詞用多少位數位表示)。在本範例中,因為只有一個句子,所以batch size為1,句子中有6個詞,所以sequence length為6,embedding dimension是我們預先設定好的值4,也就是Embedding類範例化時的第一個引數。
2.2 位置編碼器:Position Embedding層¶
無論是那種語言,中文也好,英語也罷,詞彙位置(順序)的差異,可能導致語意上的天差地別。例如,「我欠銀行一個億」與「銀行欠我一個億」,兩句話中每個單獨的詞彙拎出來語意上都麼有任何區別,但是,整句話表達出來的意思,一個天堂,一個地獄。所以,在上文Embedding向量基礎上,新增位置資訊,可以進一步提升模型效能。
新增位置資訊有兩種方式:
1. 通過網路來學習;
2. 預定義一個函數,通過函數計算出位置資訊;
在《Attention is all you need》論文原文中表示,兩種方式效果基本一致,但第二種方式可以減少模型引數量,同時還能適應即使在訓練集中沒有出現過的句子長度,所以使用第二種方式。並給出計算位置資訊的函數公式:
$$PE(pos, 2i)=sin(\frac{pos}{10000^{\frac{2i}{d}}})$$$$PE(pos, 2i+1)=cos(\frac{pos}{10000^{\frac{2i}{d}}})$$式中,$pos$表示詞彙在句子中的位置,$d$表示詞向量維度,也就是上文Embedding類中的d_model,$2i$代表的是$d$中的偶數維度,$2i + 1$則代表的是奇數維度,這種計算方式使得每一維都對應一個正餘弦曲線。
為什麼使用三角函數呢?
由於三角函數的性質: $sin(a+b) = sin(a)cos(b) + cos(a)sin(b)$、 $cos(a+b) = cos(a)Cos(b) - sin(a)sin(b)$,於是,對於位置$pos+k$ 處的資訊,可以由 $pos$ 位置計算得到,作者認為這樣可以讓模型更容易地學習到位置資訊。
這種方式編碼又為什麼能夠代表不同位置資訊呢?
由公式可知,每一維$i$都對應不通週期的正餘弦函數:$i=0$時是週期為$2π$的正弦函數,$i=1$時是週期為$2π$的餘弦函數,對於不同位置的詞彙$pos1$與$pos2$,若它們在某一維度$i$上有相同的編碼值,則說明這兩個位置的差值等於該維度所在的曲線的週期,即$|pos1-pos2|=T_i$。 而對於另一個維度$j(j\neq 1$,由於$T_j \neq T_i$,因此$pos1$和$pos2$在這個維度$j$上的編碼值就不會相等。因此,種編碼方式保證了不同位置在所有維度上不會被編碼到完全一樣的值,從而使每個位置都獲得獨一無二的編碼。
最後,將上一Embedding步驟輸出的向量與本次的PE向量(Position Embedding)相加即可,如圖4所示。 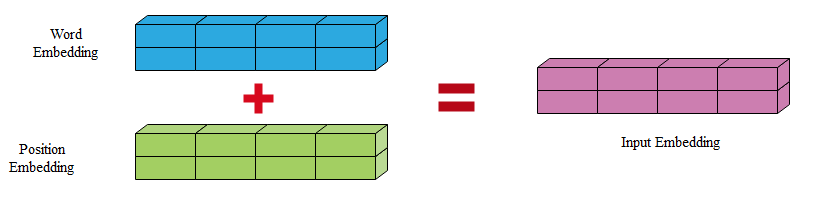
為什麼是將PE與詞向量相加,而不是拼接呢?
其實,拼接相加都可以,一般來說詞向量的維度就已經蠻大了,再拼接一個相同維度大小的位置向量,維度頓時提升一倍,這樣訓練起來會相對慢一些,影響效率。兩者的效果是差不多地,既然效果差不多當然是選擇學習習難度較小的相加了。
關於位置編碼,更加詳細的介紹,可以參看這裡。
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
"""
位置編碼器類的初始化函數
d_model:詞嵌入維度
dropout:置0比率
max_len:每個句子的最大長度
"""
super(PositionalEncoding, self).__init__()
# 範例化nn中預定義的Dropout層, 並將dropout傳入其中,獲得物件self.dropout
self.dropout = nn.Dropout(p=dropout)
# 初始化一個位置編碼矩陣,他是一個0矩陣,矩陣的大小是 max_len * d_model
pe = torch.zeros(max_len, d_model)
# 初始化一個絕對位置矩陣,在我們這裡,詞彙的絕對位置就是用它的索引去表示
# 所以我們首先使用arange方法獲得一個連續自然數向量,然後在使用unsqueeze方法拓展矩陣維度
# 又因為引數傳的是1, 代表矩陣拓展的位置,會使向量程式設計一個max_len * 1的矩陣。
position = torch.arange(0, max_len).unsqueeze(1)
# 絕對位置矩陣初始化之後,接下來就是考慮如何將這個位置資訊加入到位置編碼矩陣中
# 最簡單方法就是現將max_len * 1的絕對位置矩陣,變換成max_len * d_model形狀, 然後直接覆蓋原來的初始化位置編碼矩陣即可。
# 要實現這種矩陣變化,就需要一個1 * d_model形狀的變化矩陣div_term,我們對這個變化矩陣的要求除了形狀外,
# 還希望他能夠將自然數的絕對位置編碼縮放層足夠小的數位,有助於在之後的梯度下降過程中更快地收斂,這樣我們就可以開始初始化
# 得到一個自然數矩陣,但是我們這裡並沒有按預計的一樣的初始化一個1 * d_model的矩陣
# 只初始化了一半,即x*d_model/2的矩陣, 這是因為這裡並不是真正意義的初始化了一半的矩陣
# 我們可以把它看作初始化了兩次,而兩次初始化的變化矩陣不同的處理
# 並把這兩個矩陣分別填充在位置編碼矩陣的偶數和奇數位置上,組成最終的位置編碼矩陣。
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(1000.0)/ d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
# 這樣我們就得到了位置編碼矩陣pe, pe現在還只是一個二維矩陣,要想和embeddding的輸出(一個三維矩陣)
# 就必須坨鎮一個維度,所以這裡使用unsequeeze拓展維度
pe = pe.unsqueeze(0) # 將二維蟑螂擴充為三維張量
# 最後把pe位置編碼矩陣註冊層模型的buffer,什麼是buffer呢
# 我們把它認為是對模型效果有幫助的,但是卻不是模型結構中超引數或者引數,不需要說著優化步驟進行更新的增益
# 註冊之後我們就可以在模型儲存後重新載入時盒模型結構與引數已通被載入
self.register_buffer('pe', pe)
def forward(self, x):
"""
forward函數的桉樹是x,表示文字序列的詞嵌入表示
"""
# 在相加之前我們對pe做一些適配工作,將這個三維張量的第二位也就是句子最大長度的那一維度切片與輸入的x的第二維相同即x.size(1)
# 因為我們預設max_len為5000,一般來講是在太大了,很難有一個句子包含5000詞彙,所以要進行與輸入轉給你來那個的適配
# 最後使用Variable進行封裝,使其與x的樣式相同,但是他是不需要進行梯度求解的,因為這裡的位置資訊使用的是函數計算方式,且這一步中只是數位相加,因此把requuires_grad設定成False。
x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
# 最後就使用self.dropout物件驚喜‘丟棄’操作,並返回結果
return self.dropout(x)
pe = PositionalEncoding(4, dropout, 1000)
pe_result = pe(embr)
print("pe_result:", pe_result)
print("shape: ", pe_result.shape)
pe_result: tensor([[[-1.2341, 2.8071, 0.9948, 1.6479],
[-1.8214, 3.1610, 0.6464, -1.3914],
[-0.0975, 0.0000, 0.0000, 1.6454],
[ 1.2171, 1.3929, 0.7160, -2.4252],
[-2.4677, 0.0000, -0.6298, -1.2646],
[-2.1292, 3.7195, 5.8113, -0.0000]]], grad_fn=<MulBackward0>)
shape: torch.Size([1, 6, 4])
新增位置編碼的過程只是兩個矩陣相加,並不會改變輸出結果的shape,所以輸出結果的shape依然是[1, 6, 4]。
Transformer中,掩碼張量的主要作用在後續的注意力機制計算過程中,有一些生成的attention張量中的值計算有可能已知了未來資訊而得到的,未來資訊被看到是因為訓練時會把整個輸出結果都一次性進行Embedding,但是理論上解碼器的的輸出卻不是一次就能產生最終結果的,而是一次次通過上一次結果綜合得出的,因此,未來的資訊可能被提前利用。所以,Attention中需要使用掩碼張量掩蓋未來資訊。
我們可以這麼來理解掩碼張量的作用:我們建模目的,就是為了達到預測的效果,所謂預測,就是利用過去的資訊(此前的序列張量)對未來的狀態進行推斷,如果把未來需要進行推斷的結果,共同用於推斷未來,那叫抄襲,不是預測,當然,這麼做的話訓練時模型的表現會很好,但是,在測試(test)時,模型表現會很差。
如何進行遮掩呢?我們可以建立一個與需要被遮掩張量相同size的張量,即掩碼張量,掩碼張量中元素一般只有0和1,代表著對應位置被遮掩或者不被遮掩,至於是0位置被遮掩還是1位置被遮掩可以自定義,因此它的作用就是讓另外一個張量中的一些數值被遮掩,或者說被替換。一般來說,是被替換成一個非常小的數位(負無窮)。為什麼用非常小的數位呢?掩碼操作一般是在計算注意力得分後,softmax操作之前,被遮掩就是為了最小化被分配的注意力,那麼被遮掩的位置替換成一個非常小的數值,下一步進行softmax操作後,被遮掩的位置就成了一個趨近於0的概率時,即分配的注意力趨近於0,也就達到了被遮掩的目的。
下面我們嘗試使用pytorch實踐掩碼的原理:
atten_data = torch.randint(low=0, high=10, size=(4, 5))
atten_data
tensor([[5, 9, 0, 4, 4],
[7, 4, 5, 5, 0],
[4, 9, 4, 5, 6],
[0, 2, 6, 2, 6]])
mask = np.ones(shape=(4, 5))
mask
array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
# 假設只遮掩下三角部分,那麼將mask的下三角部分修改為0
mask = np.triu(mask, k=1)
mask = torch.from_numpy(mask)
mask
tensor([[0., 1., 1., 1., 1.],
[0., 0., 1., 1., 1.],
[0., 0., 0., 1., 1.],
[0., 0., 0., 0., 1.]], dtype=torch.float64)
# 被遮掩後的張量
atten_data.masked_fill(mask==1,-1e9)
tensor([[ 5, -1000000000, -1000000000, -1000000000, -1000000000],
[ 7, 4, -1000000000, -1000000000, -1000000000],
[ 4, 9, 4, -1000000000, -1000000000],
[ 0, 2, 6, 2, -1000000000]])
接下來,實現Transformer中的掩碼:
def subsequent_mask(size):
"""
生成向後遮掩的掩碼張量,引數size是掩碼張量最後兩個維度的大小,最後兩維形成一個方陣
"""
# 在函數中,首先定義掩碼張量的形狀
attn_shape = (1, size, size)
# 然後使用np.ones方法想這個形狀中新增1元素,形成上三角陣,最後為了節約空間
# 再使用其中的資料型別變為無符號8為整型unit8
sub_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
# 最後將numpy型別轉化為torch中的tensor,內部做一個1 - 的操作
# 在這個其實是做了一個三角陣的反轉,subsequent_mask中的每個元素都會被1減,
# 如果是0, subsequent_mask中的該位置由0變1
# 如果是1, subsequent_mask中的該位置由1變0
return torch.from_numpy(1 - sub_mask)
mask = subsequent_mask(4)
mask
tensor([[[1, 0, 0, 0],
[1, 1, 0, 0],
[1, 1, 1, 0],
[1, 1, 1, 1]]], dtype=torch.uint8)
3.2 注意力機制¶
什麼是注意力?
我們觀察事物時,之所以能夠快速做出判斷,是因為我們大腦能夠將注意力能夠以高解析度接收於圖片上的某個區域,並且以低解析度感知其周邊區域,並且視點能夠隨著時間而改變,換句話說就是人眼通過快速掃描全域性影象,找到需要關注的目標區域(在閱讀文字時就是快速掃描全文,然後找到關鍵段落、關鍵詞),然後對這個區域分配更多注意,目的在於獲取更多細節資訊和抑制其他無用資訊,從而快速作出判斷,而並非是從頭到尾的觀察一遍事物後,才能有判斷結果。
正是基於人類大腦這一特點,進行仿生,從而提出了深度學習中的注意力機制。在神經網路中,注意力機制可以認為是一種資源分配的機制,可以理解為對於原本平均分配的資源根據物件的重要程度重新分配資源,重要的單位就多分一點,不重要或者不好的單位就少分一點。
怎麼將這種能力遷移到計算機上呢?
我們通過一個類比來說明:我們需要去定做一件衣服,想好需要的衣服後,我們去到服裝店,把我們對衣服的關鍵性描述($query$,$Q$)告訴老闆,例如「男士襯衫、格子襯衫、純棉」,隨後,老闆在腦海裡將我們的描述與店裡所有衣服樣品($value$,$V$)的描述($key$,$K$)進行對比,然後拿出相對更加匹配的樣品給我們看,看了之後,我們就發現,有些衣服有50%(權重)符合我們的心意,有些衣服只有20%符合我們心意,難道我們選擇最滿意的一件嗎?不是,我們告訴老闆,這件樣品,你取這50%的特點,那件樣品,取另外20%的特點,直到湊成100%(加權平均的過程),也就是完整衣服的特徵,最後那件湊成的衣服,就是我們想要的衣服(注意力值)。
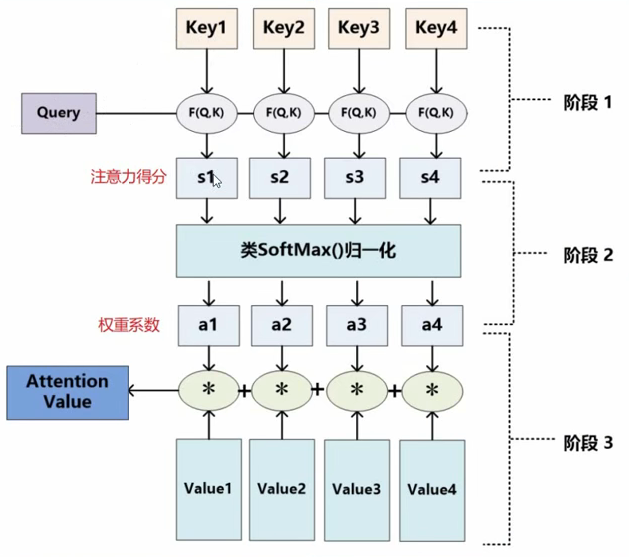
Transformer演演算法中的注意力機制,跟這個定做衣服的過程是很類似的。這裡有三個很關鍵的概念,也就是上面提到的$query$(來自源資料)、$key$(來自目標資料)、$value$(來自目標資料),這裡用「來自」這個詞有些不太準確,因為$query$、$key$、$value$是通過源資料、目標資料(都是矩陣)與不同的矩陣($W^Q$, $W^K$, $W^V$)相乘得到,放在神經網路中就是經過線性層變換。$query$、$key$、$value$三者之間是存在聯絡的,聯絡越緊密(越相似),那麼權重就越大,最終獲得的注意力就越多,所以,怎麼來評判它們之間的相似度就很關鍵了。最簡單的,就是使用餘弦相似度,但是這裡,我們更多的是使用點積的方式,兩個向量越相似,點積就越大。獲得點積之後,進行softmax操作,然後再與$value$矩陣進行加權求和,就獲得了最終整個序列的注意力值。整個過程如圖5所示。公式表示如下:
$$Attention(Q, K, V)=softmax(\frac{QK^T}{\sqrt[]{d_k}})$$式中,$d_k$為輸入樣本維度數,除以$\sqrt[]{d_k}$是為了對最終注意力值大小進行規範化,使注意力得分貼近於正態分佈,有助於後續梯度下降求解。
Transformer中的注意力機制又不僅於此,Transformer還是用了一種自注意力機制,這種注意力機制中$query$、$key$、$value$三者都是同一矩陣經過變化得來,當然,再簡化一點,直接使用初始資料矩陣作為$query$、$key$、$value$也不是不行。
這個過程很重要,是Transformer的核心,我們再用更加數學化的方式表述一遍。假設存在序列資料集$X=\{x_1, x_2, x_3, …, x_T\}$(可以認為$x_1$是文字中的第一個詞),$X$經過詞嵌入和位置編碼後,轉為為$\{a_1, a_2, a_3, …, a_T\}$,我們分別使用$W^Q$, $W^K$, $W^V$與之相乘,獲得$q_i$,$k_i$,$v_i$,$i \in (1, 2, 3, …, T)$。以$x_1$為例,如何獲得$x_1$的注意力值呢?
-
首先,我們用$x_1$對應的$query$即$q_1$與$k_1, k_2, k_3, …, k_T$計算向量點積, 得到$\alpha_{11}, \alpha_{12}, \alpha_{12}, …, \alpha_{1T}$。注意,這時候的,$\alpha_{11}, \alpha_{12}, \alpha_{12}, …, \alpha_{1T}$在取值範圍上,可未必在[0, 1]之間,還需要經過softmax處理;
-
然後,將$\alpha_{11}, \alpha_{12}, \alpha_{12}, …, \alpha_{1T}$輸入softmax層,從而獲取值在[0, 1]之間的注意力權重值,即$\hat \alpha_{11}, \hat \alpha_{12}, \hat \alpha_{12}, …, \hat \alpha_{1T}$,這相當於一個概率分佈矩陣;
-
最後,將$\hat \alpha_{11}, \hat \alpha_{12}, \hat \alpha_{12}, …, \hat \alpha_{1T}$分別與對應的$v_1, v_2, v_3, …, v_T$相乘,然後求和,這樣便獲得了與輸入的$x_1$相對應的注意力值$b_1$。
經過注意力機制層後,輸出矩陣中的每個詞向量都含有當前這個句子中所有詞的語意資訊,這對提升模型效能是極為關鍵的。
注意力機制實現過程程式碼如下所示:
def attention(query, key, value, mask=None, dropout=None):
"""
注意力機制的實現,輸入分別是query,key,value,mask:掩碼張量,
dropout是nn.Dropout層的範例化物件,預設為None
"""
# 在函數中,首先去query的最後一維的大小,一般情況下就等同於我們的詞嵌入維度,命名為d_k
d_k = query.size(-1)
# 按照注意力公式,將query與key的轉置相乘,這裡面key是將最後兩個維度進行轉置(轉置後才滿足矩陣乘法),key轉置之後shape為[1, 4, 6],[1, 6, 4] * [1, 4, 6] = [1, 6, 6]
# 再除以縮放係數,就得到注意力得分張量scores
scores = torch.matmul(query, key.transpose(-2, -1)) // math.sqrt(d_k)
# 接著判斷是否使用掩碼張量
if mask is not None:
# 使用tensor的masked_fill方法,將掩碼張量和scores張量每個位置一一比較,如果掩碼張量
# 則對應的scores張量用-1e9這個值來替換
scores = scores.masked_fill(mask == 0, -1e9)
# 對scores的最後一維進行softmax操作,使用F.softmax方法,第一個引數softmax物件,第二個
# 這樣獲得最終的注意力張量
p_attn = F.softmax(scores, dim=-1)
# 之後判斷是否使用dropout進行隨機置零
if dropout is not None:
# 將p_attn傳入dropout物件中進行「丟棄」處理
p_attn = dropout(p_attn)
#最後,根據公司將p_atten與value張量向曾獲得最終的query注意力表示,同時返回注意力權重張量
return torch.matmul(p_attn, value), p_attn
pe_result
tensor([[[-3.1567, 2.5706, -3.2771, 1.9592],
[ 1.1270, -0.6587, -0.0000, -1.9875],
[-2.1464, 0.9971, -3.2068, 0.0000],
[ 0.6572, 1.2629, 4.3154, 0.6823],
[-4.4194, -2.4844, 0.1543, 0.0000],
[-0.0000, 1.0162, -0.9905, -0.6031]]], grad_fn=<MulBackward0>)
query = key = value = pe_result
attn, p_attn = attention(query, key, value)
p_attn # 注意力權重分佈矩陣,矩陣中每一行的和為1
tensor([[[9.9752e-01, 5.5889e-09, 2.4726e-03, 2.0560e-09, 6.1290e-06,
2.2547e-06],
[1.8057e-03, 7.2848e-01, 3.6269e-02, 9.8589e-02, 3.6269e-02,
9.8589e-02],
[8.7814e-01, 3.9867e-05, 1.1884e-01, 2.6862e-07, 2.1767e-03,
8.0076e-04],
[3.0588e-07, 4.5397e-05, 1.1253e-07, 9.9993e-01, 6.1438e-06,
1.6701e-05],
[1.2338e-04, 2.2598e-06, 1.2338e-04, 8.3132e-07, 9.9975e-01,
2.2598e-06],
[3.8420e-01, 5.1996e-02, 3.8420e-01, 1.9128e-02, 1.9128e-02,
1.4134e-01]]], grad_fn=<SoftmaxBackward0>)
attn # 注意力值
tensor([[[-3.1542e+00, 2.5667e+00, -3.2769e+00, 1.9543e+00],
[ 6.4197e-01, -3.0448e-01, 2.1117e-01, -1.4365e+00],
[-3.0367e+00, 2.3713e+00, -3.2593e+00, 1.7199e+00],
[ 6.5716e-01, 1.2628e+00, 4.3150e+00, 6.8218e-01],
[-4.4189e+00, -2.4833e+00, 1.5346e-01, 2.3644e-04],
[-2.0508e+00, 1.4568e+00, -2.5456e+00, 5.7720e-01]]],
grad_fn=<UnsafeViewBackward0>)
p_attn.shape
torch.Size([1, 6, 6])
attn.shape
torch.Size([1, 6, 4])
注意力權重矩陣p_attn的shape為[1, 6, 6],與shape為[1, 6, 4]的value相乘後,輸出結果的shape回到了[1, 6, 4],並未發生變化。
3.3 多頭注意力機制¶
上文說到,自注意力機制中$query$、$key$、$value$都是通過同一資料做矩陣變換獲得,這就會造成一個問題:模型在對當前位置的資訊進行編碼時,會過度的將注意力集中於自身的位置。換句話說就是自己與自己的相似度肯定很高,從而獲得極高的注意力,而忽略其他內容。這顯然並不合理。Transformer作者採取的一種解決方案就是採用多頭注意力機制(MultiHeadAttention)。同時,使用多頭注意力機制還能夠給予注意力層的輸出包含有不同子空間中的編碼表示資訊,從而增強模型的表達能力(從不同角度去觀察,獲得更加豐富的資訊)。
多頭注意力機制為什麼有效呢?我們也可以類比理解一下,讓一個同學閱讀一篇文章60分鐘,對比讓6個同學每個閱讀10分鐘,然後彙總多個同學的理解那種方式獲取到的資訊多呢?應該是第二種,每個人的思維方式、角度總是不一樣的,從多種角度看問題獲取到的資訊更多。多頭注意力自己就是這麼個思路。
那麼,多頭注意力機制怎麼實現的呢?使用多頭注意力機制後,我們需要將$query$、$key$、$value$分割為$h$份,$h$為頭的數量,分割前$query$、$key$、$value$的shape為[batch size, sequence length, embedding dimension],分割後,shape為[batch size, sequence length, h, embedding dimension / h], 為了方便後續運算,我們對sequence length, h這兩個維度進行轉置,轉置後shape為[batch size, h, sequence length, sequence length],再softmax後與$value$相乘,輸出shape為[batch size, h, sequence length, embedding dimension / h],reshape後,shape回到[batch size, sequence length, embedding dimension],依然是最初的shape。
這裡之所以不厭其煩地多次提到不同階段shape,是因為從shape的變換上,可以看出整個多頭注意力機制的過程。很多材料上說,多頭注意力機制就是使用多組$query$、$key$、$value$計算注意力,我認為這種說法不準確,應該說是對$query$、$key$、$value$進行劃分,獲得多組更小的$query$、$key$、$value$,獲得多組注意力進行組合。可以參考這篇文。
# 首先需要定義克隆函數,因為在多頭注意力機制的實現中,用到多個結構相同的線形層
# 我們將使用clone函數將他們已通初始化在同一個網路層列表物件中,之後的結構中也會用到該函數
def clone(model, N):
# 用於生成相同網路層的克隆函數,它的引數module表示要克隆的目標網路層,N代表需要克隆的數量
# 在函數中,我們通過for迴圈對module進行N次深度拷貝,使其每個module稱為獨立的層
return nn.ModuleList([copy.deepcopy(model) for _ in range(N)])
# 我們使用一個類來實現多頭注意力機制的處理
class MultiHeadAttention(nn.Module):
def __init__(self, head, embedding_dim, dropout=0.1):
"""
在類的初始化時,會傳入三個引數,head代表頭數,embedding_dim代表詞嵌入的維度,dropout代表進行dropout操作時置零比率,預設是0.1
"""
super(MultiHeadAttention, self).__init__()
# 在函數中,首先使用了一個測試中常用的assert語句,判斷h是否能被d_model整除
# 這是因為我們之後要給每個頭分配等量的詞特徵,也就是embedding_dim//head個
assert embedding_dim % head == 0
self.head = head # 傳入頭數
self.embedding_dim = embedding_dim
self.dropout = nn.Dropout(p=dropout)
self.d_k = embedding_dim // head # 得到每個頭獲得的分割詞向量維度d_k
# 然後獲得線形層物件,通過nn的Linear範例化,它的內部變化矩陣是embedding_dim * Embedding_dim
self.linears = clone(nn.Linear(embedding_dim, embedding_dim), 4)
self.attn = None
def forward(self, query, key, value, mask=None):
"""前向邏輯函數,它的輸入引數有4個,前三個就是注意力機制需要的Q、K、V,
最後一個是注意力機制中可能需要的mask掩碼張量,預設是None"""
if mask is not None: # 如果存在掩碼張量
mask = mask.unsqueeze(0) # 使用unsqueeze拓展維度,代表多頭中的第n頭
# 接著,我們獲得一個batch_size的變數,它是query尺寸的第1個數位,代表有多少條樣本
batch_size = query.size(0)
# 之後就進入多頭處理環節
# 首先利用zip將輸入QKV與三個線形層組到一起,然後使用for迴圈,將輸入QKV分別傳入到線形層中
# 完成線性變換後,開始為每個頭分割輸入,這裡使用view方法對線性變化的結果進行維度重塑
# 這樣就意味著每個頭可以獲得一部分詞特徵組成的句子,其中的-1代表自適應維度
# 計算機會根據這種變換自動計算這裡的值,然後對第二維和第三維進行轉置操作
# 為了讓代表句子長度維度和詞向量維度能夠相鄰,這樣注意力機制才能找到遲疑與句子位置的關係
# 從attention函數中可以看到,利用的是原始輸入的倒數第一和第二,這樣我們就得到了每個頭的
print('----------------------------------')
print('query-before transpose: ', query.shape)
print('key-before transpose: ', key.shape)
print('value-before transpose: ', value.shape)
# 此時,query, key, value的shape為[1, 6, 4], [batch size, sequence length, embedding dimension]
query, key, value = \
[model(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2)
for model, x in zip(self.linears, (query, key, value))]
print('----------------------------------')
print('query-after transpose: ', query.shape)
print('key-after transpose: ', key.shape)
print('value-after transpose: ', value.shape)
print('----------------------------------')
# 此時,query, key, value的shape修改為:[1, 2, 6, 2] , [batch size, sequence length, h, embedding dimension / h]
# 得到每個頭的輸入後,接下來就是將他們傳入attention中
# 這裡直接呼叫我們之前實現的attention函數,同時也將mask和dropout傳入其中
x, self.attn = attention(query, key, value, mask, self.dropout)
print('x- after attention: ', x.shape) # 經過注意力機制後,輸出x的shape為:[1, 2, 6, 2], [batch size, h, sequence length, embedding dimension / h]
# 通過多頭注意力計算後,我們就得到了每個頭計算結果組成的4維張量,我們需要將其轉換為輸入的
# 因此這裡開始進行第一步處理環節的逆操作,先對第二和第三維驚喜轉置,然後使用contiguous方法
# 這個方法的作用就是能夠讓轉置後的張量應用view方法,否則將無法直接使用
# 所以,下一步就是使用view方法重塑形狀,變成和輸入形狀相同
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.head * self.d_k) # 對x進行reshape
print('x', x.shape) # x的shape回到[1, 6, 4], [batch size, sequence length, embedding dimension]
return self.linears[-1](x)
# 範例化若干引數
head = 2
embedding_dim = 4
dropout = 0.2
# 若干輸入引數的初始化
query = key = value = pe_result
mha = MultiHeadAttention(head, embedding_dim, dropout)
mha_result = mha(query , key, value)
print('mha_result:', mha_result.shape)
---------------------------------- query-before transpose: torch.Size([1, 6, 4]) key-before transpose: torch.Size([1, 6, 4]) value-before transpose: torch.Size([1, 6, 4]) ---------------------------------- query-after transpose: torch.Size([1, 2, 6, 2]) key-after transpose: torch.Size([1, 2, 6, 2]) value-after transpose: torch.Size([1, 2, 6, 2]) ---------------------------------- x- after attention: torch.Size([1, 2, 6, 2]) x torch.Size([1, 6, 4]) mha_result: torch.Size([1, 6, 4])
3.4 前饋全連線層¶
完成多頭注意力計算後,考慮到此前一系列操作對複雜過程的擬合程度可能不足,所以,通過增加全連線層來增強模型的擬合能力。前饋全連線層對應於圖1中「Feed Forward」所標識的元件。
class PositionalwiseFeedForward(nn.Module):
def __init__(self, d_model, d_ff, dropout=0.1):
"""
d_model: 線形層的輸入維,因為我們希望輸入通過前饋全連線層後輸入和輸出的維度不變
d_ff: 第二個線形層
droupout:置零比率
"""
super(PositionalwiseFeedForward, self).__init__()
# 首先按照我們預期使用nn範例化了兩個線形層物件
# 他們的引數分別是d_model, d_ff和d_ff, d_model
self.w1 = nn.Linear(d_model, d_ff)
self.w2 = nn.Linear(d_ff, d_model)
# 然後我們使用nn的Dropout範例化了物件self.dropout
self.dropout = nn.Dropout(p=dropout)
def forward(self, x):
"""輸入引數為x,代表來自上一層的輸出"""
# 首先經過第一個線性層,然後使用Funtional中relu函數進行啟用,
# 之後再使用dropout進行隨機置0,最後通過第二個線性層w2,返回最終結果.
return self.w2(self.dropout(F.relu(self.w1(x))))
3.5 規範化層¶
所有深層網路模型都需要用到標準網路層,因為隨著網路層數的增加,通過多層的計算後引數可能開始出現過大或過小的情況,這樣可能會導致學習過程出現異常,模型可能收斂非常的慢。因此都會在一定層數後接規範化層進行數值的規範化,使其特徵數值在合理範圍內。規範化層對應於圖1中「Add & Norm 」所標識的元件。
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
# features:詞嵌入的維度
# eps:一個足夠小的數,在規範化公式的分母中出現,房子分母為0。
super(LayerNorm, self).__init__()
# 根據features的形狀初始化兩個引數張量a2和b2,a2為元素全為1的張量,b2為元素全為0的張量。這兩個張量就是規範化層的引數
# 因為直接對上一層得到的結果做規範化公式計算,將改變結果的正常表徵,因此就需要有引數作為調節因子
# 使其既能滿足規範化要求,又能不改變針對目標的表徵,最後使用nn.parameter封裝,代表它們是模型的引數
self.eps = eps
self.a2 = nn.Parameter(torch.ones(features))
self.b2 = nn.Parameter(torch.zeros(features))
def forward(self, x):
# x來自於上一層的輸出
# 在函數中,首先對輸入變數x求其最後一個維度的均值,並保持輸出維度與輸入維度一致
# 接著再求最後一個維度的標準差,然後就是根據規範化公式,用x減去均值除以標準差獲得規範化的結果
# 最後對結果乘以我們的縮放茶樹,即a2, *號代表同型點乘,即對應位置進行乘法操作,加上位移引數b2返回即可
#
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a2 * (x - mean) / (std + self.eps) + self.b2
3.6 子層連線結構¶
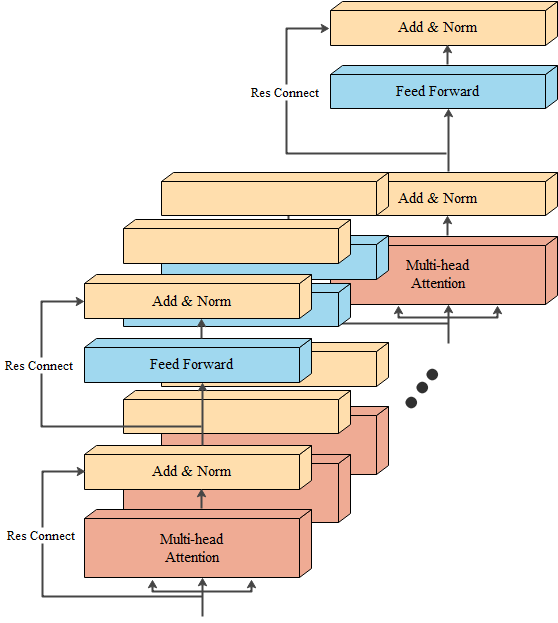
輸入到每個子層以及規範化層的過程中,還使用了殘差連線,我們把這一部分結構整體叫做子層連線(代表子層及其連線結構),在每個編碼器層中,都有兩個子層,這兩個子層加上週圍的連結結構就形成了兩個子層連線結構。如圖6所示,為Transformer結構中的兩個子層連線結構,這兩個結構在同一個編碼器層中上下相連。無論是在編碼器中,還是在解碼器中,子層連線結構都是重要的元件。
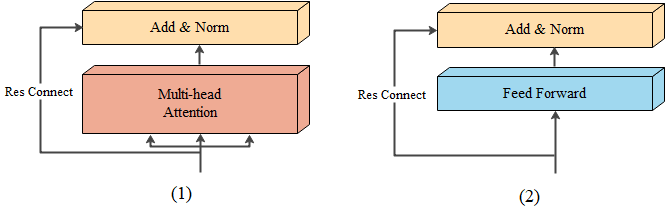
class SubLayerConnection(nn.Module):
def __init__(self, size, dropout=0.1):
# size: 詞嵌入的維度大小
# dropout:隨機置零比率
super(SubLayerConnection, self).__init__()
self.size = size
self.dropout = nn.Dropout(p=dropout)
# 範例化了規範化物件self.norm
self.norm = LayerNorm(size)
def forward(self, x, sublayer):
# 前向邏輯函數中,接收上一層或者子層的輸入作為第一個引數
# 將該子層連線中的子層函數作為第二個函數
# 我們首先對輸出進行規範化,然後將結果傳給子層處理,之後再對子層進行dropout操作
# 隨機停止一些網路中神經元的作用,來房子過擬合,最後還有一個add操作
# 因為存在跳躍連線,所以是將輸入x與dropout後的子層輸出結果相加作為最終的子層連線輸出
return x + self.dropout(sublayer(self.norm(x)))
3.7 編碼器層¶
作為編碼器的組成單元, 每個編碼器層完成一次對輸入的特徵提取過程, 即編碼過程。編碼器層結構如圖7所示。
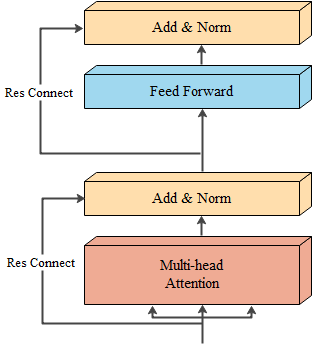
class EncoderLayer(nn.Module):
def __init__(self, size, self_attn, feed_forward, dropout):
# size:詞嵌入維度的大小
# self_attn:傳入多頭注意力子層範例化物件,並且是自注意力機制
# feed_forward:前饋全連線層範例化物件
# dropout:置零比率
super(EncoderLayer, self).__init__()
self.size = size
# 首先將self_attn和feed_forward傳入其中
self.self_attn = self_attn
self.feed_forward = feed_forward
self.dropout = nn.Dropout(p=dropout)
# 編碼器層中有兩個子層連線結構,所以使用clones函數進行克隆
self.sublayer = clone(SubLayerConnection(size, dropout), 2)
def forward(self, x, mask):
# x:上一層輸出
# mask:掩碼張量
# 裡面就是按照結構圖左側的流程,首先通過第一個子層連線結構,其中包含多頭注意力子層,然後通過第二個子層連線結構,
#其中包含前饋全連線子層,最後返回結果
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
class Encoder(nn.Module):
def __init__(self, layer, N):
# layer:編碼器層
# N: 編碼器層的個數
super(Encoder, self).__init__()
# 首先使用clones函數克隆N個編碼器層放在self.layers中
self.layers = clone(layer, N)
# 再初始化一個規範化層,將用在編碼器的最後面
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
# forward函數的輸入和編碼器層相同,x代表上一層的輸出,mask代表掩碼張量
# 首先就是對我們克隆的編碼器層進行迴圈,每次都會得到一個新的x
# 這個迴圈的過程,就相當於輸出的x經過N個編碼器層的處理
# 最後在通過規範化層的物件self.norm進行處理,最後返回結果
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
4 解碼器模組¶
我們先來思考一個問題?我們為什麼要新增解碼器模組,編碼器後面直接接全連線層或者殘差結構、迴圈網路層不可以嗎?
不是不可以,只是效能要降低很多。一方面是在Transformer的解碼器模組中,使用了多個解碼器(Transformer的paper中說是6個),每個解碼器都創新地使用了多頭注意力機制,這裡的注意力機制還比編碼器模組中的多頭注意力機制豐富,多個注意力機制層資料來源不同($query$、$key$、$value$);另一方面,在Transformer的解碼器訓練過程中使用了「teacher-forcing」這麼一種訓練方式,teacher-forcing是指在訓練網路過程中,每次不使用上一個階段的輸出作為下一個階段的輸入,而是直接使用訓練資料的標準答案(目標資料)的對應上一項作為下一個階段的輸入。teacher-forcing不是本文的重點,不做過多討論。
解碼器模組具體怎麼運作的呢?下面我們結合解碼器模組的元件結構來說明。
4.1 解碼器層¶
解碼器模組由6個解碼器層組成,每個解碼器層等結構完全一樣,如圖9所示:
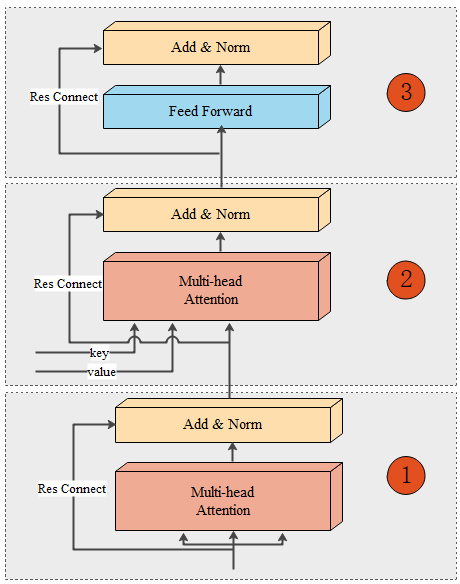
每個解碼器層由三個子層連線結構組成:
(1) 第一個子層連線結構包括一個多頭注意力子層和規範化層以及一個殘差連線。在訓練時,因為有目標資料可用,所以第一個解碼器層多頭注意力子層的輸入來自於目標資料,上文提到過,這種機制叫做「teacher-force」,但是在測試時,已經沒有目標資料可用了,那麼,輸入資料就來自於此前序列的解碼器模組輸出,沒有預測過,那麼就是起始標誌的編碼。同時,注意這裡的注意力是自注意力,也就是說$query$、$key$、$value$都來自於目標資料矩陣變化得來,然後計算注意力,另外,這裡計算注意力值時,一定使用掩碼操作。後續的5個解碼器層的輸入資料是前一個解碼器層的輸出。
(2) 第二個子層連線結構包括一個多頭注意力子層和規範化層以及一個殘差連線。編碼器的輸出的結果將會作為$key$、$value$傳入每一個解碼器層的第二個子層連線結構,而$query$則是當前解碼器層的上一個子層連線結構的輸出。注意,這裡的$query$、$key$、$value$已經不同源了,所以不再是自注意力機制。完成計算後,輸出結果作為第三個子層連線結構的輸入。
(3) 第三個子層連線結構包括一個前饋全連線子層和規範化層以及一個殘差連線。完成計算後,輸出結果作為輸入進入下一個解碼器層。如果是最後一個解碼器層,那麼輸出結果就傳入輸出模組。
class DecoderLayer(nn.Module):
def __init__(self, size, self_attn, src_attn, feed_forward, dropout=0.1):
# size:詞嵌入的維度大小,同時也代表解碼器層的尺寸
# self_attn:多頭注意力物件,也就是說這個注意力機制需要Q=K=V
# src_attn:多頭注意力物件,這裡Q!=K=V
# feed_forward:前饋全連線層物件
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.dropout = nn.Dropout(p=dropout)
# 按照結構圖使用clones函數克隆三個子層連線物件
self.sublayer = clone(SubLayerConnection(size, dropout), 3)
def forward(self, x, memory, source_mask, target_mask):
# x:來自上一層的輸出
# mermory:來自編碼器層的語意儲存變數
# 源資料掩碼張量和目標資料掩碼張量
m = memory
# 將x傳入第一個子層結構,第一個子層結構分別是x和self-attn函數,因為是自注意力機制,所以Q,K,V都是x
# 最後一個引數的目標資料掩碼張量,這是要對目標資料進行遮掩,因為此時模型可能還沒有生成任何目標資料
# 比如紮起解碼器準備生成第一個字元或者詞彙時,我們其實已經傳入了第一個字元以便計算損失
# 但是我們不希望在生成第一個字元時模型還能利用這個資訊,因此我們會將其遮掩,同樣生成第二個字元或詞彙時
# 模型只能使用第一個字元或者詞彙資訊,第二個字元以及之後的資訊都不允許模型使用
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, target_mask))
# 接著進入第二個子層,這個職稱中常規的注意力機制,q是輸入x;k,v是編碼層輸出的memory
# 同樣也傳入source_mask,但是進行源資料遮掩的原因並非是抑制資訊洩露,而是這筆掉對結果沒有意義的字元而陳勝的注意力值
# 以此提升模型效果和訓練速度,這樣就完成了第二個子層的處理
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, source_mask))
# 最後一個子層就是前饋全連線子層,經過它的處理後,就可以返回結果,這就是我們的解碼器層結構。
return self.sublayer[2](x, self.feed_forward)
4.2 解碼器¶
解碼器就是將6個解碼器層進行堆疊。第一個解碼器層接受目標資料作為輸入,後續的解碼器使用前序一個解碼器層的輸出作為輸入,通過這種方式將6個解碼器層連線。最後一個解碼器層的輸出將進入輸出模組。
class Decoder(nn.Module):
def __init__(self, layer, N):
# layer:解碼器層layer
# N:解碼器層的個數N
super(Decoder, self).__init__()
# 首先使用clones方法克隆了N個layer,然後範例化了一個規範化層
# 因為資料走過了所有的解碼器層後,最後要做規範化處理
self.N = N
self.layers = clone(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, source_mask, target_mask):
# x:資料的嵌入表示
# memory:編碼器層的輸出
# source_mask:源資料掩碼張量
# target_mask:目標資料掩碼張量
# 對每個層進行迴圈,淡然這個迴圈就是變數x通過每一個層的處理
# 得出最後的結果,再進行一次規範化返回即可
for layer in self.layers:
x = layer(x, memory, source_mask, target_mask)
return self.norm(x)
5 輸出模組¶
輸出模組的結構就很簡單了,如圖10所示。
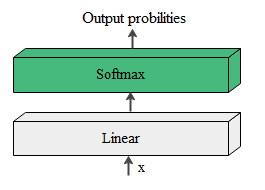
- 線形層
通過對解碼器模組的輸出進行線性變化得到指定維度的輸出, 也就是轉換維度的作用。
- softmax層
使最後一維的向量中的數位縮放到0-1的概率值域內, 並滿足他們的和為1。
我們繼續以漢譯英模型為例,說一說輸出模組是怎麼將一系列的張量轉化為一個個的詞彙了。假設我們目標資料有1000個英文單詞,線形層接收到解碼器模組最終輸出矩陣後,將會輸出一個長度為1000的張量,其中每一個元素對應詞彙表中一個單詞。將這個張量繼續傳入softmax層中進行softmax操作,轉換為概率分佈矩陣。概率分佈矩陣最大值所對應的單詞即為此時模型翻譯的輸出結果。
# nn.functional工具包裝載了網路層中那些只驚喜年計算,而沒有引數的層
# 將線形層和softmax計算層一起實現,因為二者的共同目標是生成最後的結構
# 因此把類的名字叫做Generator,生成器類
class Generator(nn.Module):
def __init__(self, d_model, vocab_size):
# d_model:詞嵌入維度
# vocab_size:詞表大小
super(Generator, self).__init__()
# 首先就是使用nn中的預定義線形層進行範例化,得到一個物件self.project等待使用
# 這個線性層的引數有兩個,計時初始化函數時傳進來的 d_model和vocab_size
self.vocab_size = vocab_size
self.embedding_dim = embedding_dim
self.project = nn.Linear(d_model, vocab_size)
def forward(self, x):
# 前向邏輯函數中輸入是上一層輸出張量x
# 在函數中,首先使用上一步得到的self.project對x進行線性變化
# 然後使用F中已經實現的log_softmax進行的softmax處理
return F.log_softmax(self.project(x), dim=-1)
6 模型構建¶
通過上面的四個模組的介紹,我們已經完成了所有組成模組的原理介紹和實現 接下來就來實現完整的編碼器-解碼器結構。
# 編碼器-解碼器結構實現
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder, source_embed, target_embed, generator):
# encoder:編碼器物件
# decoder:解碼器物件
# source_embed:源資料嵌入函數
# target_embed:目標資料嵌入函數
# generator:輸出部分的類別生成器物件
super(EncoderDecoder, self).__init__()
# 將引數傳入類中
self.encoder = encoder
self.decoder = decoder
self.src_embed = source_embed
self.tgt_embed = target_embed
self.generator = generator
def encode(self, source, source_mask):
# 使用src_embed對source做處理,然後和source_mask一起傳給self.encoder
return self.encoder(self.src_embed(source), source_mask)
def decode(self, memory, source_mask, target, target_mask):
# 解碼函數
# 使用tgt_embed對target做處理,然後和source_mask、target_mask、memory一起傳給self.decoder
return self.decoder(self.tgt_embed(target), memory, source_mask,
target_mask)
def forward(self, source, target, source_mask, target_mask):
# source:源資料
# target:目標資料
# source_mask、target_mask:對應的掩碼張量
# 在函數中,將source、source_mask傳入編碼函數,得到結果後,與source-mask、target、target_mask一同傳給解碼函數
return self.decode(self.encode(source, source_mask), source_mask,
target, target_mask)
堆疊成一個完整的Transformer模型:
def make_model(source_vocab, target_vocab, N=6, d_model=512,
d_ff=2048, head=8, dropout=0.1):
# source_vocab:源資料特徵(詞彙)總數
# target_vocab:目標資料特徵(詞彙)總數
# N:編碼器和解碼器堆疊數
# d_model:詞向量對映維度
# d_ff:前饋全連線網路中變化矩陣的維度
# head:多頭注意力機制中多頭數
# dropout:置零比率
# 首先得到一個深度拷貝命令,接下來很多結構都要進行深度拷貝,從而保證它們彼此之間相互獨立,不受干擾
c = copy.deepcopy
# 範例化了多頭注意力機制類,
attn = MultiHeadAttention(head, d_model, dropout)
# 然後範例化前饋全連線類
ff = PositionalwiseFeedForward(d_model, d_ff, dropout)
# 範例化位置編碼器類
position = PositionalEncoding(d_model, dropout)
# 根據結構圖,最外層是EncoderDecode,在EncoderDecoder中
# 分別是編碼器層,解碼器層,源資料Embedding層和位置編碼組成的有序結構
# 目標資料Embedding層和位置編碼組成的有序結構,以及類別生成器層
# 在編碼器層中有attention子層以及前饋全連線子層
# 在解碼器層中有兩個attention子層以及前饋全連線層
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
nn.Sequential(Embedding(d_model, source_vocab), c(position)),
nn.Sequential(Embedding(d_model, target_vocab), c(position)),
Generator(d_model, target_vocab))
# 模型構建完成後,接下來就是初始化模型中的引數,比如線形層的變化矩陣
# 這裡一旦判斷引數的維度大於1,則會將其初始化成為一個服從均勻分佈的矩陣
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model

作者:奧辰
微訊號:chb1137796095
Github:https://github.com/ChenHuabin321
歡迎加V交流,共同學習,共同進步!
本文版權歸作者和部落格園共有,歡迎轉載,但未經作者同意必須保留此段宣告,且在文章頁面明顯位置給出原文連結,否則保留追究法律責任的權利。