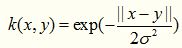深入淺出理解SVM支援向量機演演算法
支援向量機是Vapnik等人於1995年首先提出的,它是基於VC維理論和結構風險最小化原則的學習機器。它在解決小樣本、非線性和高維圖形識別問題中表現出許多特有的優勢,並在一定程度上克服了「維數災難」和「過學習」等傳統困難,再加上它具有堅實的理論基礎,簡單明瞭的數學模型,使得支援向量機從提出以來受到廣泛的關注,並取得了長足的發展 。支援向量機(Support Vector Machine, SVM)本身是一個二元分類演演算法,是對感知機演演算法模型的一種擴充套件,現在的 SVM 演演算法支援線性分類和非線性分類的分類應用,並且也能夠直接將 SVM 應用於迴歸應用中,同時通過 OvR 或者 OvO 的方式我們也可以將 SVM 應用在多元分類領域中。在不考慮整合學習演演算法,不考慮特定的資料集的時候,在分類演演算法中 SVM 可以說是特別優秀的。
SVM演演算法思想
支援向量機最初是在圖形識別中提出的。假定訓練樣本集合(xi, yi),i-1,… ,l, xi∈R ,y∈{-1,+1},可以被超平面x·w+b=0無錯誤地分開 ,並且離超平面最近的向量離超平面的距離是最大的 ,則這個超平面稱為最優超平面。 對於下圖哪條分界線最好,這便是SVM要解決的問題

假設未來拿到的資料含有一部分噪聲,那麼不同的超平面對於噪聲的容忍度是不同的,最右邊的線是最 robust 的。
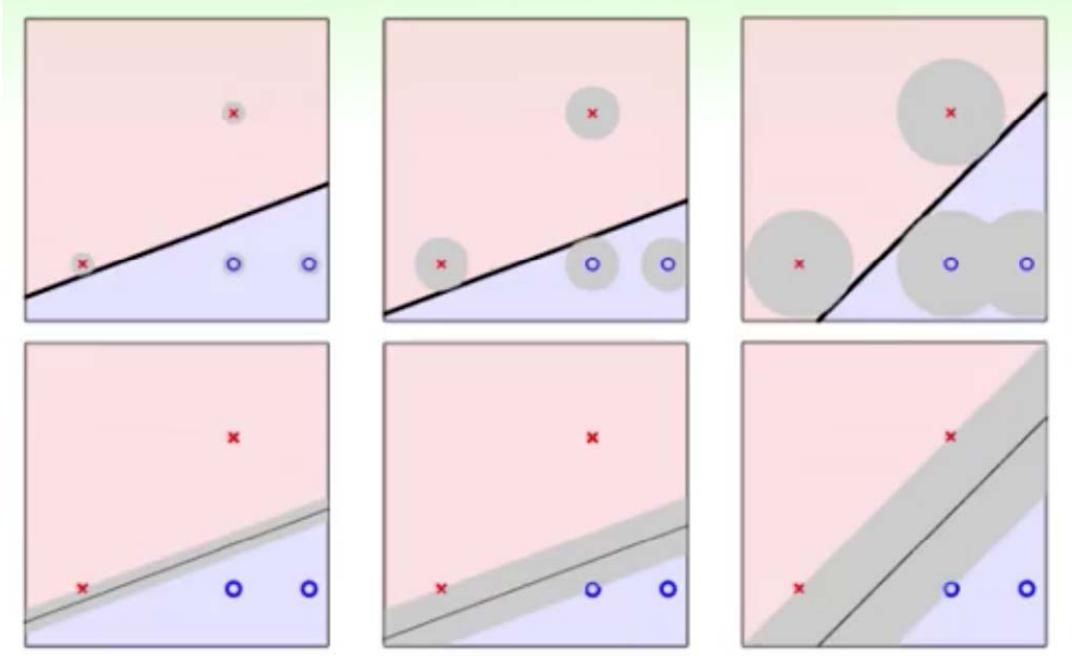
所以說我們只要讓離超平面比較近的點儘可能的遠離這個超平面,那麼我們的模型分類效果應該就會比較不錯。SVM 其實就是這個思想。
函數間隔
在超平面確定的情況下,
可以相對地表示點
距離超平面的遠近。對於兩類分類問題,如果
,則
的類別被判定為1;否則判定為-1。所以如果
,則認為
的分類結果是正確的,否則是錯誤的。且
的值越大,分類結果的確信度越大。反之亦然。所以樣本點
與超平面
之間的函數間隔定義為
。但是該定義存在問題:即
和
同時縮小或放大M倍後,超平面並沒有變化,但是函數間隔卻變化了。所以,需要將
的大小固定,如
,使得函數間隔固定。這時的間隔也就是幾何間隔 。
幾何間隔
定義超平面關於樣本點(xi,yi)的幾何間隔為:
實際上,幾何間隔就是點到超平面的距離。高中學習的點到直線
的距離公式:
所以在二維空間中,幾何間隔就是點到直線的距離。在三維及以上空間中,就是點到超平面的距離。而函數距離,就是上述距離公式中的分子,即未歸一化的距離。
定義訓練集到超平面的最小几何間隔是:
可以發現函數間隔與幾何間隔有如下關係:
![]()
當我們取分母即W的L2範數為1時,函數間隔和幾何間隔相等。
如果超平面引數w和b成比例地改變(超平面沒有改變),函數間隔也按此比例改變,而幾何間隔不變。
SVM訓練分類器的方法是尋找到超平面,使正負樣本在超平面的兩側,且樣本到超平面的幾何間隔最大。所以SVM可以表述為求解下列優化問題:
以上關於間隔問題在《統計學習方法》中有詳細講解
線性可分支援向量機
給定一個線性可分的訓練資料集,通過間隔最大化或等價地求解相應的凸二次規劃問題學習得到的分離超平面為:
w · x + b = 0
決策函數為:
f(x)=sign(wx+b)
在二維空間上,兩類點被一條直線完全分開叫做線性可分。
硬間隔最大化
我們尋找的超平面應當滿足:這個超平面不僅可以將資料集中的所有正負範例點分開,而且對最難區分的範例點(離超平面最近的點,也就是支援向量)也有足夠大的間隔將它們分開。
尋找幾何間隔最大的分離超平面問題可表示為下面的約束最佳化問題:
![]()
![]()
即我們要最大化超平面關於資料集T的幾何間隔γ,約束條件則表示訓練集中每個點與超平面的幾何間隔都大於等於γ。
事實上我們就是要找到一對支援向量(一正例一負例兩個樣本點,超平面在這兩個點的正中間,使得超平面對兩個點的距離最遠),同時這個超平面對於更遠處的其他所有正負範例點都能正確區分。
可將上式的幾何間隔用函數間隔表示,這個問題可改寫為:
![]()
![]()
此時如果我們將w和b放大λ倍,那麼右邊的函數間隔也會放大λ倍。也就是說約束條件左右兩邊都整體放大了λ倍,對不等式約束沒有影響。因此,我們不妨取:
![]()
取1是為了方便推導和優化,且這樣做對目標函數的優化沒有影響。
那麼上面的最佳化問題變為:
![]()
![]()
最大化1/||w||與最小化(1/2)||w||2 是等價的,乘以1/2是為了後面求導時計算方便。
則我們可以得到下面的線性可分支援向量機學習的最佳化問題:
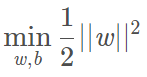
![]()
線性可分支援向量機的原始問題轉化為對偶問題
我們將上面最佳化問題稱之為原始問題
我們可以列出一個拉格朗日函數來求解原始問題。我們定義拉格朗日函數為:

原始問題是一個極小極大問題
![]()
直接求原始問題並不好解,我們可以應用拉格朗日對偶性,通過求解對偶問題來得到原始問題的最優解。
對偶問題求解過程
根據拉格朗日對偶性,對偶問題是極大極小問題,即求:
![]()
對偶問題的求解過程:
先對L(w,b,α)求對w、b的極小。我們需要求L對w、b的偏導數並令其為0。
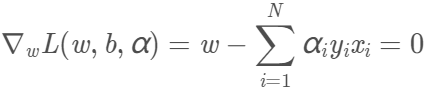
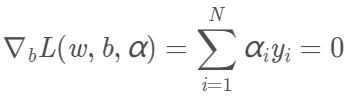
得到兩個等式:
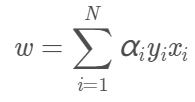

將上面兩式代入拉格朗日函數,得:

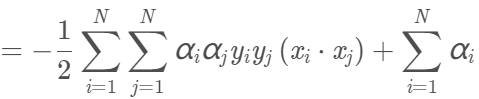
再求min L(w,b,α)對α的極大,即:
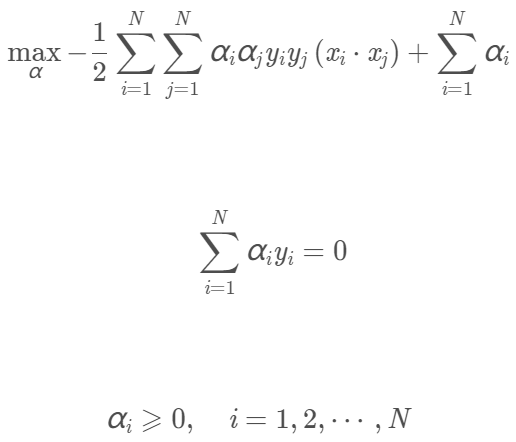
我們將上面第一個式子乘以-1,即可得到等價的對偶最佳化問題:
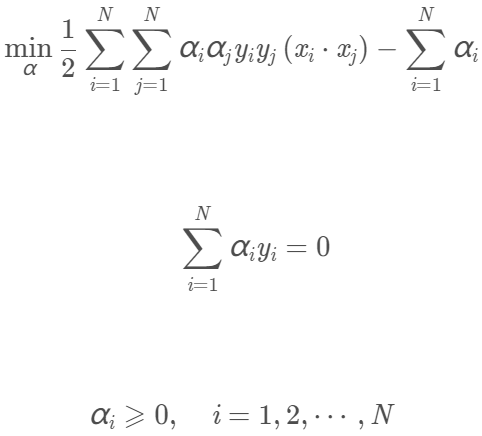
我們可以求出上面問題對α的解向量(α即為所有拉格朗日乘子)為:
![]()
則按上面求L對w、b的偏導數並令其為0得到的等式,我們可得:
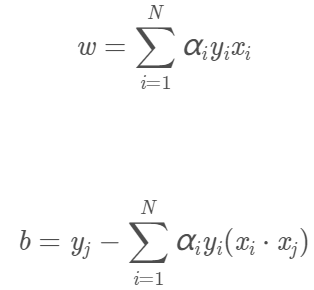
那麼超平面就為
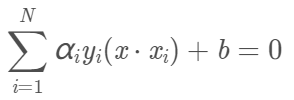
決策函數為
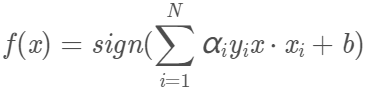
我們注意到對原始的最佳化問題:
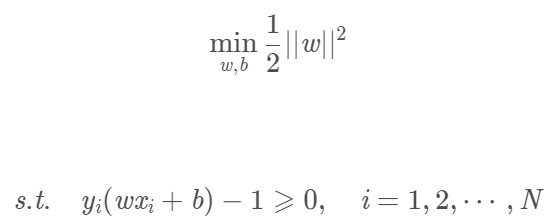
有不等式約束,因此上述過程必須滿足KKT條件:
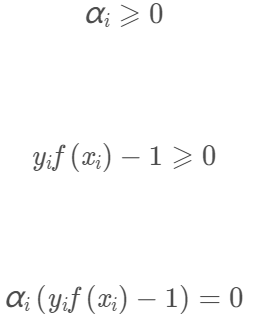
線性支援向量機
我們經常遇到這樣的情況:資料集T中大部分傳輸線性可分,但有少部分傳輸線性不可分,這時使用上面的線性可分支援向量機並不可行。這時我們就要使用學習策略為軟間隔最大化的線性支援向量機。
軟間隔最大化
所謂軟間隔最大化,就是在硬間隔最大化的基礎上,對每個樣本點(xi, yi)引進一個鬆弛變數ξi,於是我們的約束不等式變為:
![]()
同時,我們的目標函數中對每個鬆弛變數ξi需要支付一個代價ξi
即目標函數變為:

這裡C>0稱為懲罰引數。C較大時對誤分類的懲罰增大,C較小時對誤分類的懲罰減小。
上面的目標函數包含兩層含義:一是使間隔儘量大,二是使誤分類點的個數儘量小。
鬆弛變數ξi表示xi在超平面下不符合真實分類,但是與超平面距離<ξi,因此我們將其歸到另一類(也就是真實分類)。鬆弛變數用來解決異常點,它可以"容忍"異常點在錯誤的區域,使得支援向量機計算出的超平面不至於產生過擬合的問題,但同時,我們又不希望鬆弛變數太大導致超平面分類效能太差。
線性支援向量機的原始問題轉化為對偶問題
原始問題
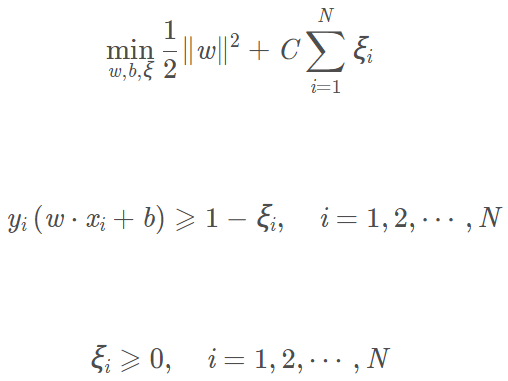
對偶問題及解題過程
原始問題的對偶問題為:
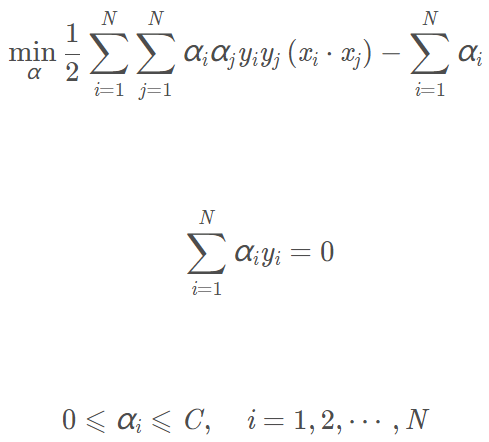
拉格朗日函數為:
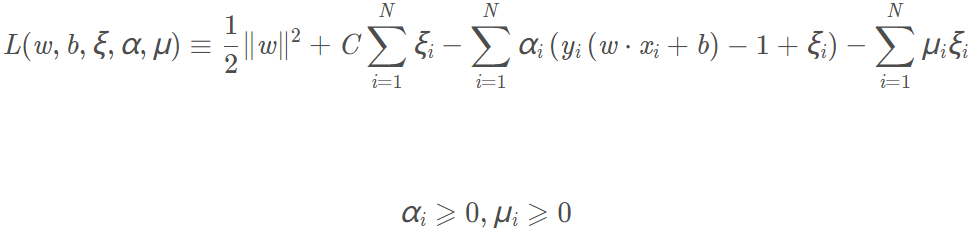
類似的,先求L對w、b、ξ的極小,求L對w、b、ξ的偏導數並令偏導數為0,最後得:
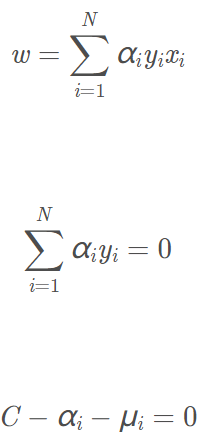
上面三式代回L,得:
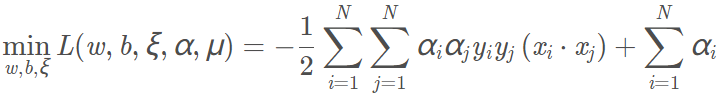
再對上式求α的極大,得到對偶問題:
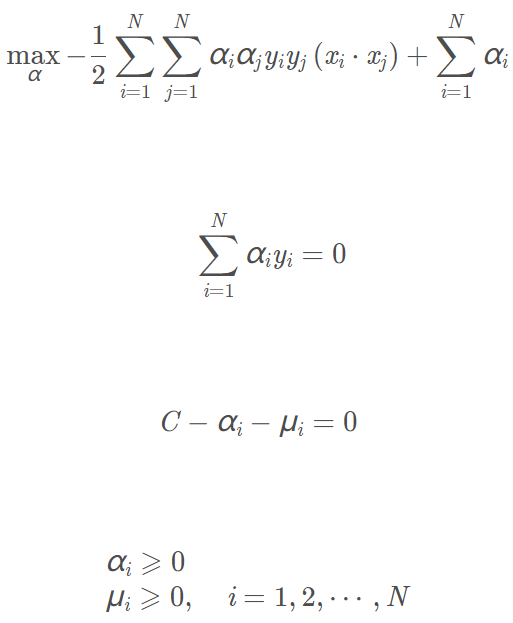
設
![]()
是上面對偶問題的拉格朗日乘子的解,那麼有:
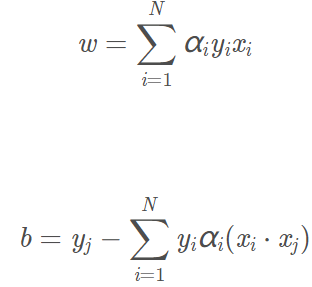
那麼超平面為:
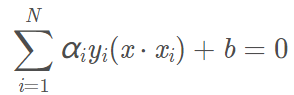
決策函數為:
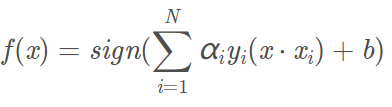
非線性支援向量機
如果我們的資料集樣本是非線性可分的,我們可以使用一個對映將樣本從原始空間對映到一個合適的高維空間,在這個高維空間中資料集線性可分。
核函數(Kernel Function)
設X是輸入空間,H是特徵空間(即高維空間),如果存在一個對映:
![]()
使得
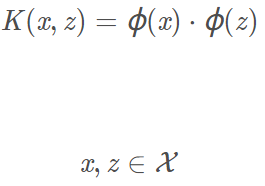
那麼稱K(x,z)為核函數。Φ(x)為對映函數,等式右邊是內積。
常用的核函數:
1. Linear Kernel
線性核是最簡單的核函數,核函數的數學公式:k(x, y) = xt · y
2. Polynomial Kernel
多項式核實一種非標準核函數,它非常適合於正交歸一化後的資料,其具體形式:k(x, y) = (axt y+c)d 比較好用的,就是引數比較多,但是還算穩定
3. Gaussian Kernel
這裡說一種經典的魯棒徑向基核,即高斯核函數,魯棒徑向基核對於資料中的噪音有著較好的抗干擾能力,其引數決定了函數作用範圍,超過了這個範圍,資料的作用就「基本消失」。高斯核函數是這一族核函數的優秀代表,也是必須嘗試的核函數,其數學形式如下:
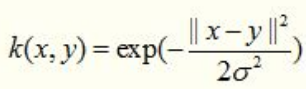
雖然被廣泛使用,但是這個核函數的效能對引數十分敏感
4. Exponential Kernel
指數核函數就是高斯核函數的變種,它僅僅是將向量之間的L2距離調整為L1距離,這樣改動會對引數的依賴性降低,但是適用範圍相對狹窄。其數學形式如下:
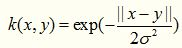
5. Sigmoid Kernel
Sigmoid 核來源於神經網路,現在已經大量應用於深度學習,它是S型的,所以被用作於「啟用函數」,表示式:k(x, y) = tanh(axty+c)
核技巧
現在假設我們用對映:
![]()
將超平面從原本低維空間的形式變成高維空間的形式:
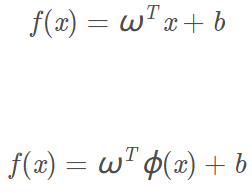
這時我們原本在低維的非線性邊界在高維就變成了一個超平面,在高維中資料集變得線性可分了。
但是如果我們先將資料集從低維對映到高維,再去求超平面,由於高維空間中維數要多的多,計算量會變得很大。
核技巧是一種方法,我們用它可以簡化計算。它就是用低維空間的內積來求高維空間的內積,省去了先做對映變換再在高維空間中求內積的麻煩。
舉例:
以多項式核為例,若樣本x有d個分量:
![]()
我們做一個二維的多項式變換,將d維擴充套件:
![]()
注意上面的式子中有很多重複項可以合併。
我們對變換後的樣本作內積:

其中,最後一項可以拆成:
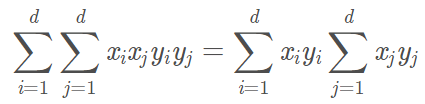
又低維空間的內積可表示為:
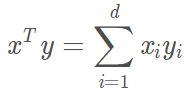
所以上面變換後的多項式內積可以寫成:
![]()
我們就可以不先進行高維變換,再在高維空間做內積,而是直接利用低維空間的內積計算即可。
SVM中的核技巧:
不使用核函數時支援向量機的最佳化問題為:
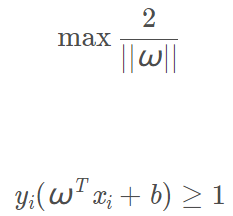
使用核函數將資料集樣本從低維對映到高維空間後最佳化問題變為:
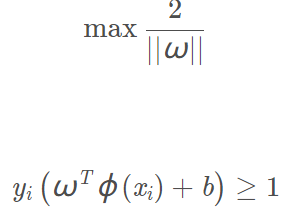
於是我們可以得到類似的對偶問題:
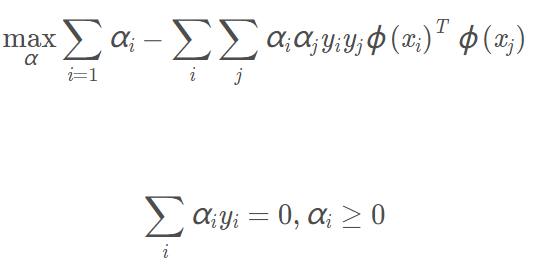
我們在計算其中的
![]()
內積時就可以使用核技巧。使用核函數表示對偶問題為:
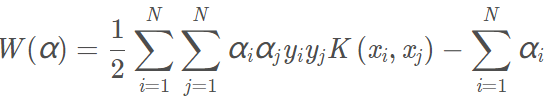
分類決策函數表示為:
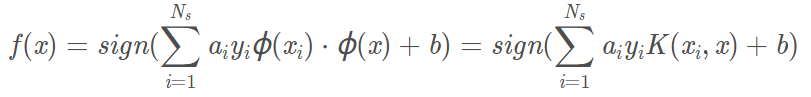
SVM演演算法小結
SVM 演演算法是一個很優秀的演演算法,在整合學習和神經網路之類的演演算法沒有表現出優越效能之前,SVM 演演算法基本佔據了分類模型的統治地位。目前在巨量資料時代的大樣本背景下,SVM由於其在大樣本時超級大的計算量,熱度有所下降,但仍然是一個常用的機器學習演演算法。
優點:
1) 解決高維特徵的分類問題和迴歸問題很有效,在特徵維度大於樣本數時依然有很好的
效果。
2) 僅僅使用一部分支援向量來做超平面的決策,無需依賴全部資料。
3) 有大量的核函數可以使用,從而可以很靈活的來解決各種非線性的分類迴歸問題。
4) 樣本量不是海量資料的時候,分類準確率高,泛化能力強。
缺點:
1) 如果特徵維度遠遠大於樣本數,則 SVM 表現一般。
2) SVM 在樣本量非常大,核函數對映維度非常高時,計算量過大,不太適合使用。
3) 非線性問題的核函數的選擇沒有通用標準,難以選擇一個合適的核函數。
4) SVM 對缺失資料敏感。